刚柔耦合机械手的抓握姿态和力综合优化方法

2024-01-13王天磊冯李航孙振兴柯云李超超胡记伟

浙江大学学报（工学版） 2023年12期

王天磊，冯李航，孙振兴，柯云，李超超，胡记伟

(1.南京工业大学电气工程与控制科学学院，江苏南京 211816；2.长兴华强电子股份有限公司，浙江湖州 313119)

随着科学技术的发展，机械手在工业和人类生活中扮演的角色愈发重要，帮助人类完成抓取、搬运、操作等工作[1-3].传统的机械手大多为刚性机械手，使用刚性材料和刚性驱动方式，精度高、输出力大，但在环境和人员交互方面存在一定安全隐患.使用柔性材料或柔性结构制成的柔性机械手凭借其灵活性、交互安全性、环境适应性等优点，正受到越来越多的研究者的关注[4].

柔性机械手驱动方式多种多样，包括流体驱动[5-7]、电磁场驱动[8]、绳或肌腱驱动[9-10]等，其中流体驱动是关注和使用最广泛的驱动方式之一.流体驱动主要分为液体和气体驱动2 种[11-12]，其中气体驱动在响应速度和执行器便捷化轻量化方面更具优势[13].气动机械手的驱动腔体多为柔性材料，每个运动自由度通常需要独立的气动腔体，腔体在正压或负压下运动或形变.由于每个气动腔体占有一定的空间体积，限制了机械手的整体结构，难以组成复杂的多关节机械手，难以进行复杂和精确的姿态调节，实现安全柔顺抓取主要依赖柔性手爪自身材料的固有柔性[14].

现有的柔性机械手大多只能抓取特定种类或形状的物体[15-17]，适用范围有限，且由于手指自由度有限，手指姿态和抓握力之间存在耦合，难以实现抓握姿态和抓握力的独立控制.当使用不合适的姿态或力进行抓取时，很容易因手指刚度不足或姿态不稳定导致抓取失败，或因手指刚度和抓握力过大而损坏抓取对象.对于采用高刚度材料设计的或加入了刚性材料的柔性机械手[18-20]，合适的抓握力和抓握姿态控制显得更加重要.此类材料尽管显著增加了机械手的有效抓握力和负载能力，但在安全性方面比柔性材料有所不足，增加了不恰当的抓握姿态和抓握力可能带来的风险.

为了解决柔性机械手的抓握姿态和抓握力控制的问题，本研究以前期研究设计的刚柔耦合机械手为平台，在前期研究提出的抓握姿态优化算法的基础上[21]，深入研究并提出综合考虑机械手的抓握力和手指姿态贴合适应性的抓握姿态优化方法.建立期望抓握力与期望手指刚度的联系，综合抓握姿态贴合度和期望刚度构建优化目标函数，对比不同期望抓握力对最优抓握姿态的影响.通过仿真和实验验证所提算法的可行性.

1 机械手设计和建模

1.1 机械手结构设计

以前期研究设计的刚柔耦合机械手为对象，机械手的详细设计方法可以参考文献[21]，机械手的整体结构如图1 所示.机械手自然状态下竖直方向长度约为190 mm，直径约为120 mm，由刚性骨架、柔性驱动单元和柔性手指3 个部分构成.刚性骨架采用铝合金材料，为整体结构提供稳定支撑和可靠的力传导.机械手的手掌（以下简称为手掌）中心气动弹簧和手指均为柔性聚氨酯材料，保证了作业的柔顺性和安全性.手掌在中心的线性气动弹簧的驱动下，可以模仿人类手掌的开合和抓握姿态调节功能，并在不主动改变手指姿态的情况下，提供额外抓握力.手掌骨架末端连接3 根手指，每根手指均由独立制作的近端指节和末端指节黏合而成.每个黏合后的完整手指包含2 个独立的气动腔体，腔体内的正负气压驱动2 个指节分别向正或反方向弯曲，为机械手提供足够的自由度以调节合适的抓握姿态.

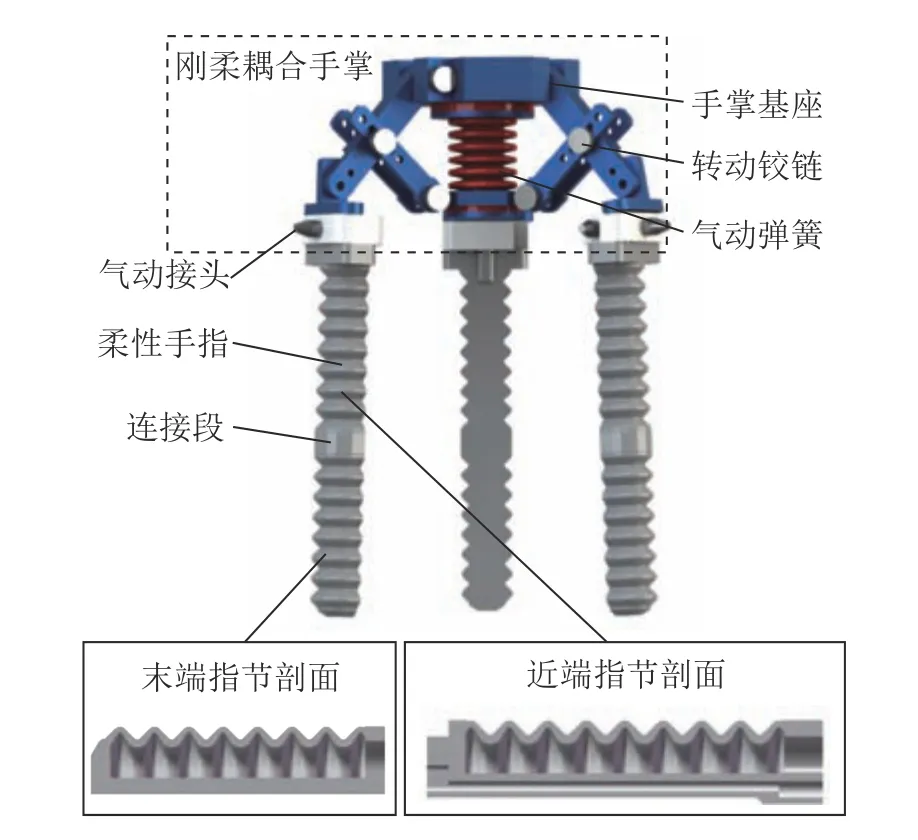
图1 刚柔耦合机械手结构Fig.1 Structure of soft-rigid robotic hand

在多路气压驱动下，机械手能够提供多种复杂的不对称抓握姿态，但本研究采用对称的方式驱动机械手，3 个近端指节和3 个末端指节分别连接2 个气动回路，3 个手指抓握时在各自的弯曲平面上具有相同的弯曲状态.相应地，后续的姿态优化方法针对轴对称物体，即物体在各个轴向竖直剖面上均具有相同的轮廓.

1.2 机械手几何建模

机械手几何模型是抓握姿态优化算法的基础，根据机械手姿态和物体的轴对称性，取单个手指的弯曲平面作为截面对1 个手指分支进行建模，如图2 所示.图中，灰色圆表示转动铰链，机械手上的粗实线为刚性连接，虚线为柔性手指曲线，中间灰色块为待抓握物体，灰色块边缘粗实线为物体轮廓曲线.坐标原点O建立在机械手掌的顶端中心，U为物体轮廓曲线，Ω1、Ω3分别为近端和末端手指曲线，Ω2为中间的连接直线段.Ω1与上端固定骨架的连接点的切线BC平行.忽略手指材料的伸长，则Ωi（i= 1, 2, 3）在弯曲时保持与物体接触面的总长度不变.刚性连接线段AB、BC'、C'C、GH的长度分别为d2、d3、d4和da，铰链G固定在刚性杆AB上，线段AG的长度为d1.柔性手指上的曲线段Ω1、Ω2、Ω3的长度分别为l1、l2、l3.半径AO和HQ的长度分别为r1和r2.

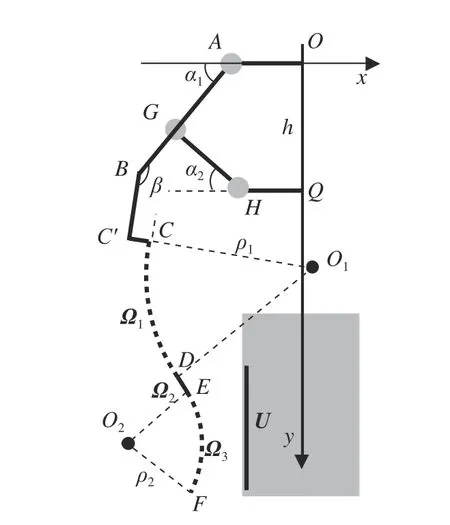
图2 单手指弯曲平面几何模型Fig.2 Single finger geometry model in bending plane

为了方便描述，使用带有符号的半径定义手指的弯曲曲率半径ρ1、ρ2，正半径代表正气压下的向中轴线侧的弯曲，负半径代表负气压下的向远离中轴线方向的弯曲.柔性手指连接点C的坐标为C(xC,yC)，其中：

Ω1弯曲后的曲率中心坐标为

Ω1的下端点D的坐标为

与D相连接的Ω2为不可弯曲的直线，其末端点E的坐标为

Ω3弯曲后的曲率中心坐标为

1.3 柔性手指刚度特性测试

实现稳定可靠的抓握要求柔性手指的刚度与机械手期望施加的抓握力相适应.为了描述柔性手指刚度与驱动气压压强的关系，进行如图3 所示的手指刚度测试实验.柔性手指固定在测试平台上方，传感器安装在位移标尺的直线滑台上，可以在对手指末端施加位移和力的同时测量位移和力的大小.每个时刻手指的近端和末端指节同时施加压强p，手指刚度以手指末端压力Ft与末端位移xt的比值来表征，标尺行进相同位移测得的Ft越大，表明手指刚度越大.由图3（c）、（d）所示的测试结果可以看出，柔性手指的刚度与其内部压强正相关.增加内部压强不但增加了手指弯曲曲率[21]，而且增加了手指刚度，更有利于在施加大抓握力的同时保持较小的手指姿态形变.因此，根据手指刚度与内部压强的正相关性，可以在抓握姿态优化算法中采用手指内部压强来表征手指刚度.

图3 柔性手指刚度测试实验Fig.3 Rigidity test of soft finger

2 抓握姿态和力综合优化算法

抓握姿态优化算法能让机械手与被抓握物体的外轮廓具有尽可能大的贴合度[21].在此基础上，本研究提出改进的姿态优化算法，以更好地兼顾抓握姿态和抓握力的要求.所提算法综合考虑与期望抓握力有关的手指期望刚度，使得机械手能够根据被抓握对象的不同物理属性调整姿态，以获得更好的抓握适应性.算法的流程框图如图4 所示.根据图2 所示的几何模型对手指和物体轮廓曲线提取采样点.对于在Ωi上任意点P的坐标，根据P所在曲线段的不同，坐标可以分别表示如下.

图4 抓握姿态和力综合优化算法流程图Fig.4 Flow chart of comprehensive optimization algorithm of gripping gesture and force

1）当P∈Ω1, 时，

2）当P∈Ω2时，

3）当P∈Ω3时，

为了使抓握更加稳定，在构造优化目标函数时综合考虑手指姿态曲线与被抓握物体轮廓曲线的贴合度，以及与期望抓握力有关的手指期望刚度.一方面，对于稳定的抓握姿态，手指曲线Ωi应与物体曲线U有尽可能大的贴合度，以保证有足够大的接触面积.另一方面，手指的刚度应能随物体特性和抓握力需求不同而不同.根据上述思想，构造综合优化目标函数和约束条件为

式中：pi（i= 1, 2）为表征手指刚度的手指内部压强；σ 为手指姿态与物体轮廓曲线贴合度；F为期望抓握力， εi>0 （i= 1, 2, 3）为抓握力系数；α1为图2 中的几何角度，与气动弹簧长度h的关系为

pi可以根据前期实验得到的拟合关系由手指的曲率半径计算得到[21]：

相应地，气动弹簧的长度与内部压强的关系为

式中：ps为气动弹簧内压强，pe为提供额外抓握力所施加的压强，ks为弹簧的等效刚度系数，S为有效截面积.σ 由手指和物体轮廓曲线段上采样点的平均距离函数来描述：

式中：xi、xi,o分别为手指和被抓握物曲线上的采样点，成对分组，共有m组.每条曲线上相邻采样点之间的距离相等.

式(11)中的优化约束条件限定了手指正负弯曲曲率均不能高于相应上下限值，即气压高压不能超过手指材料的物理强度限制，低压必须保持手指具有一定的最低刚度.与气动弹簧伸长量相关的角α1的限制确保弹簧始终工作在线性形变区.期望手指刚度应与不同期望抓握力相适应，手指刚度与内部压强呈正相关.因此，式(11)中使用系数 εi（i= 1, 2）来调节手指刚度在优化中的所占权重，实现用期望刚度调节机械手姿态的目的.附加的抓握力须通过气动弹簧的额外伸长实现，当期望抓握力大时，弹簧的初始伸长量应适当减小，因此将反映弹簧长度的α1与权重加入目标函数，为后续施加抓握力留足空间.求解式(11)可以得到该条件下机械手与物体轮廓刚好接触时的最优抓握姿态.该姿态本身并不施加抓握力，抓握力完全由额外的弹簧压力提供，但最优姿态权衡了手指刚度和贴合度，为后续将要施加的期望抓握力提供了最合适的手指姿态条件.由式(11)可以看出，当期望抓握力F较大时，优化目标会趋向获得更大的手指内部压强，即手指刚度；而当需要轻柔的抓握时F减小，指数也相应减小，甚至可以为0.

3 仿真和实验验证

使用如图5 所示的圆柱体和球体2 种典型形状的物体，通过仿真和实验来验证优化算法的效果.图中，圆柱体和球体测试件中心都安装有压力传感器，用以在实验中测量机械手抓握时手指施加的压力.

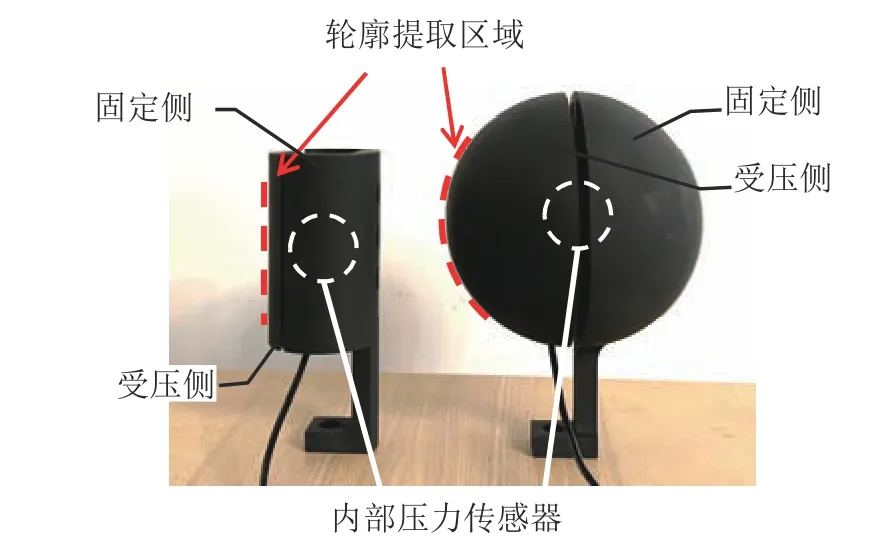
图5 抓握实验测试件结构Fig.5 Test object structures in grasping experiment

3.1 机械手抓握姿态仿真分析

使用Matlab 仿真计算不同条件下的最优抓握姿态.机械手的主要静态几何参数如表1 所示，对于球体，取 ε1= 0.8， ε2=ε3= 0.4；对于圆柱体，取ε1=1.6 ， ε2=ε3=0.8.物体的合适摆放位置会随着机械手抓握姿态的不同而有略微不同，为了对比方便，在仿真中设物体固定不动，调整机械手的位置，使机械手的不同姿态均保持手指最下端对齐进行绘图，结果如图6 所示.图中，不同形状的大点表示不同期望抓握力F下柔性手指各段曲线的连接点位置，连接不同形状大点的虚线段为对应F下的最优手指姿态曲线.不同期望抓握力F下的机械手最优姿态几何参数如表2 所示.根据式(12)～(14)，由柔性手指和气动弹簧的几何参数算出实验中相应的驱动压强.

表1 机械手主要几何参数Tab.1 Static geometry parameters of robotic hand

表2 机械手的最优抓握姿态仿真结果Tab.2 Simulation results of optimal gestures for robotic hand

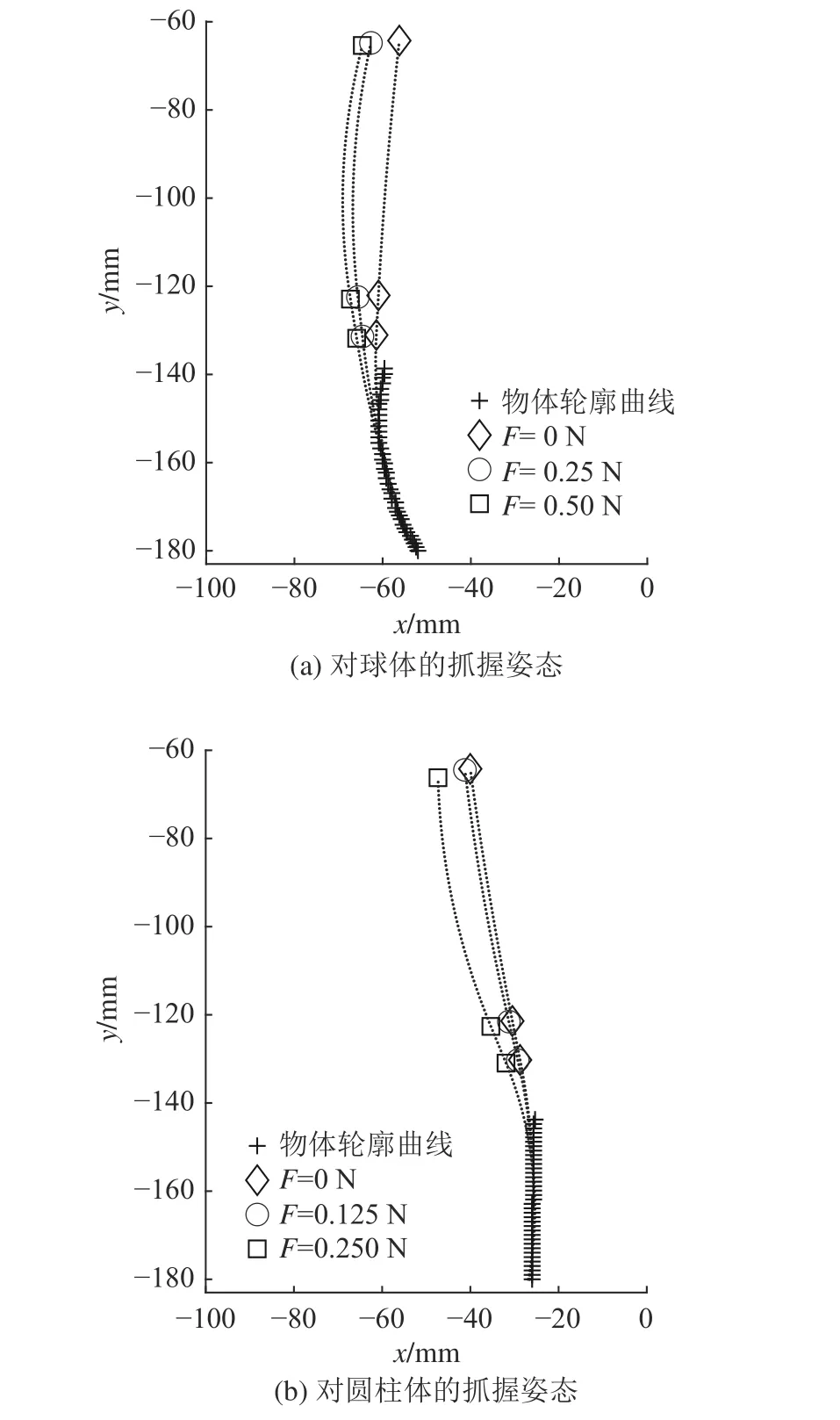
图6 机械手在不同期望力下的最优抓握姿态Fig.6 Optimized gesture of robotic hand with different expected forces

总体来说，由于手指的刚度和姿态相互关联，降低对手指的刚度要求可以获得更好的手指曲线贴合性，亦即抓握柔顺性.图6（a）为机械手在抓握直径为12 cm 的球体时的最优手指曲线.当期望力F= 0 N 时，机械手对抓握力无任何需求，手指曲线较为平直，内部压强较小，刚度较低.此时若通过手掌施加额外抓握力，则会转化为手指的形变，不易将抓握力通过手指施加到物体上，从而实现利用手指的自身材料柔性保护被抓握物体的作用.当期望力F增大时，最优姿态下各指节具有较大的曲率，即较大的内部压强和刚度.此时若施加额外抓握力，则手指可以相对较好保持其原有形状，并对物体施加较大抓握力.对于球体物体的抓握，期望力分别为0.5 N 和0.25 N 的最优姿态差异并不显著.图6（b）为机械手在抓握直径为5.2 cm 的圆柱体时的最优手指曲线.与图6（a）类似，期望抓握力越小，手指的驱动压强和曲率就越小，手指刚度也越小.相比于抓握球形物体，抓握圆柱物体时增大期望力F会更显著地改变最优姿态下的手指曲率.原因是在这种抓握需求下，目标函数式(11)中的曲线贴合度和手指刚度指标更容易达成平衡，不会因为更高的手指刚度过多牺牲手指曲线贴合性.尽管如此，增加手指刚度仍然会略微减小末端指节抓握时的贴合性，会一定程度影响抓握柔顺性.

3.2 机械手抓握实验

为了验证理论和仿真结果，进行如图7 所示的抓握实验.抓握实验依据图6 的姿态优化结果，对比不同期望抓握力下的最优姿态对实际抓握的影响.在实验中，机械手的一根手指正向压载在测试件的受压侧，测试件内部传感器直接测量单根手指对物体施加的抓握力.为了验证手指刚度对额外施加抓握力的影响，实验对比施加额外抓握力后的手指形变状况.图7（a）～（d）为机械手在抓握球体物体时的实验照片.可以看出，不同手指刚度下的最优抓握姿态均可以获得较好的姿态贴合性，其中F= 0 N 时的姿态贴合最好，且手指刚度最小，最不易损坏被抓握物.过小的手指刚度不适于施加抓握力，如图7（b）所示，在F= 0 N姿态下，施加单指0.5 N 的抓握力会使手指严重变形，导致球体无法被机械手包络，在实际应用中会使被抓取物掉落从而导致抓取失败.相比之下，F= 0.5 N 时的姿态则可以在同样的抓握力下较好地保持原有姿态，如图7（d）所示.高刚度的手指形成的手爪姿态在施加压力后仍然可以保持对球体的包络，形成较为稳定的抓握.图7（e）～（f）为机械手在抓握圆柱体物体时的实验照片.由于F= 0 N 时得到的最优姿态中气动弹簧初始伸长很大，能继续伸长并施加额外抓握力的空间较小，且手指刚度过小，无法满足施加足够的额外抓握力的要求，因此，仅对比F= 0.25 N 时的施加抓握力前后姿态.可以看出，由于抓握时手指刚度较大，施加单指0.25 N 抓握力后手指形变很小，不会对手指姿态造成太大影响.相比于几乎无法继续施加额外力的零期望抓握力下的最优姿态，显然考虑手指刚度的优化结果更具实用价值.