面向申威众核处理器的规则处理优化技术

张振东 王 彤 刘 鹏,3

1 （浙江大学信息与电子工程学院 杭州 310027）

2 （之江实验室智能超算研究中心 杭州 311100）

3 （数学工程与先进计算国家重点实验室 江苏无锡 214125）

（zhendong404@zju.edu.cn）

随着以申威系列处理器[1]和“神威·太湖之光”[2]为代表的国产处理器和国产超算性能的突飞猛进，越来越多的应用[1,3]开始利用申威处理器的主核+从核阵列的架构优势实现性能提升. 口令恢复系统因其对信息安全、国防军工的重要意义也成为了申威处理器平台上的热门研究问题.

一般口令恢复系统可以分为口令生成和口令验证2 个部分，其中口令生成负责产生可能包含正确口令的口令搜索空间，口令验证则负责验证口令搜索空间中的口令的正确性. 当前大多数基于申威处理器的口令恢复系统研究主要关注对口令验证部分的并行优化. 常见的方案是利用主核产生口令，然后将口令验证部分划分并分配给申威处理器的从核阵列，利用多个从核并行执行实现加速. 对于口令生成部分，这些研究均只采用了掩码方式生成口令. 由于掩码方式的生成速度较快，这种方案不会产生口令生成性能瓶颈，但掩码方式的猜测命中率较低，因此不能覆盖实际应用场景.

基于规则的口令生成是另一种主流的口令生成方式，相关研究[4]表明使用规则可以获得比字典和掩码方式更高的猜测命中率，因此规则模式也成为了Hashcat[5]和John the Ripper[6]等主流口令恢复工具中流行的口令生成方式. 然而由于规则处理的过程比掩码更加复杂，规则模式下的口令生成速度成为性能瓶颈. 以神威·太湖之光超算使用的SW26010 处理器为例，其单个主核的规则处理速度约为3 MPPS（million passwords per second），而SW26010 处理器单个从核阵列执行NTLM，MD5 等加密算法时速度可达到100 MPPS 以上，现有方案下申威处理器的规则模式性能大约只有其理论峰值性能的1/30.申威处理器平台上规则处理实现方案造成性能瓶颈的原因有2 个方面：一是现有方案下规则处理算法由主核完成，一个主核要负责生成64 个从核需要的口令，对于包括NTLM，MD5，SHA1 在内的众多加密算法，64 个从核每秒消耗的口令数量远大于一个主核每秒生成的口令数量；二是当前大多数加密算法都使用了申威单指令多数据流（single instruction multiple data, SIMD）指令集进行向量优化，而规则处理算法的SIMD 向量优化则缺少相关研究，因此规则处理算法的速度瓶颈表现得更加突出.

为了突破申威处理器上的规则处理速度瓶颈，进一步提升口令恢复系统的性能，增强申威处理器平台上口令恢复应用的实用性，本文提出了面向申威处理器平台的规则处理算法优化方法，主要内容和创新点包括4 点：

1） 从线程级、数据级2 个维度分析了规则处理算法的可并行度，针对申威处理器主核执行规则处理算法速度慢的问题，提出了并行任务映射机制，实现了规则处理算法的并行任务分解和从核阵列加速.

2） 针对如何高效利用从核局部数据存储器（local data memory, LDM）空间降低口令和规则数据传输开销的问题，提出了从核缓冲区配比优化机制，通过对从核数据通信量、通信时间建模，运用非线性优化理论求解了最优的口令、数据缓冲区容量配比，相比等容量分配策略使数据通信时间和通信量分别减少了40.5%和44.7%；通过变长规则存储机制减缓了规则数据冗余造成的通信开销问题，使通信时间和通信量分别下降了89.0%和89.3%.

3） 针对从核间计算量分配不均匀导致的加速比下降问题提出了负载均衡机制，使负载不均匀情况下的规则处理整体执行时间减少了13.5%.

4） 针对现有规则函数实现不能充分利用申威SIMD 指令集优势的问题，提出了41 种规则函数的SIMD向量优化方案，结合不同类型规则函数的计算访存模式，利用申威SIMD 指令集提供的特殊指令实现了大小写转换、字符匹配、字符移动等操作的向量优化，将部分规则函数执行的时钟周期降低了50%.

实验结果表明，应用本文提出的优化方案后，现有口令恢复系统的规则模式口令恢复速度在不同规则集下提升了30～101 倍.

1 研究背景与相关工作

1.1 申威处理器指令集架构

图1 展示了神威·太湖之光超算中使用的申威系列SW26010 处理器的核组架构[7]. 每个核组包含一个主核和一个从核阵列，每个从核阵列由8 行8 列共64 个从核组成. 核组内部，主核与从核阵列的运行频率均为1.5 GHz，每个主核包含5 条整数流水线和2条SIMD 浮点流水线. 主核的L1 指令缓存、L1 数据缓存均为32 KB，L2 缓存大小为512 KB.从核阵列中每个从核包含1 条整数流水线和1 条SIMD 流水线.每个从核还配备了64 KB 的LDM，从核访问LDM 的开销为4 个时钟周期，因此LDM 被广泛用于缓存外部主存中的数据. 在存储器方面，每个核组可通过本地存储控制器访问8 GB DDR3 外部存储器. 主核与从核阵列可以离散地访问外部存储器中的数据，也可以通过直接存储访问（direct memory access, DMA）方式批量访问从而提高访存性能.

Fig.1 Architecture of a SW26010 processor core group图1 SW26010 处理器核组架构

指令集方面SW26010 处理器采用了申威自主设计的64 b 精简指令集体系架构，该指令集除了支持常用的标量8 b，16 b，32 b，64 b 整数运算和单精度、双精度浮点运算外，还支持256 b 的SIMD 向量指令.利用申威SIMD 指令集，SW26010 处理器每个从核每个时钟周期最多可以完成8 次单精度浮点运算或4次双精度浮点运算或8 次32 b 整数运算. 此外，申威SIMD 指令集还支持256 b 整数运算指令，此时SIMD 向量寄存器中的数据被视为1 个256 b 的整数，对该整数可以进行逻辑左移、逻辑右移等操作. 合理利用此类指令可以高效地实现规则处理算法中的部分规则函数.

1.2 规则与规则函数

在口令生成领域，规则本质上是一种形式化描述语言. 一条规则由1 个或多个规则函数组成，这些规则函数可以实现对口令的修改、截取、扩展、复制等操作.表1 列举了Hashcat 中部分常用的规则函数，完整的规则函数列表可见Hashcat 官网[8]. 每个规则函数都使用一个字符作为其标识符，例如“u”“T”“*”“r”“^”. 部分规则函数在其标识符后面还跟随了1 个或2 个字符组成的参数，例如“^X”的参数为X，“*NM”的参数为N和M. 通过分析真实的泄露口令库的特征并将其表达成各种规则函数的组合形式，基于规则的口令恢复成为了最灵活、准确且高效的口令恢复方式[8].

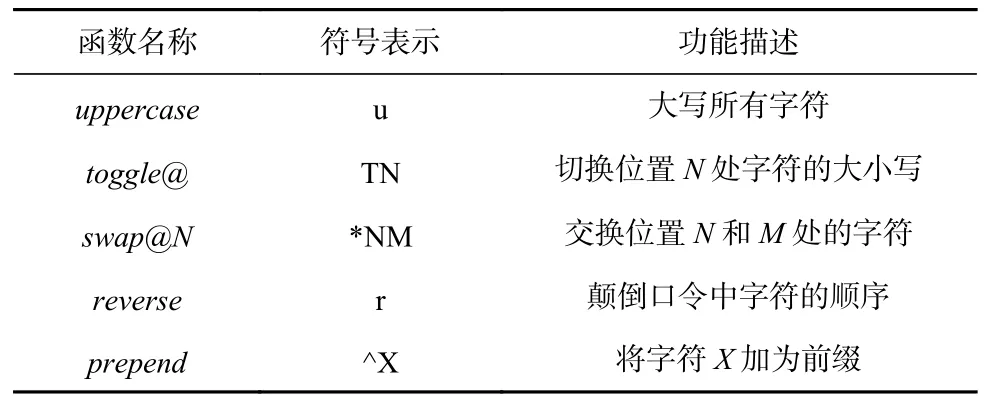
Table 1 Part of the Frequently Used Rule Functions表1 常用的部分规则函数

1.3 基于规则处理的口令生成过程

在Hashcat 和John the Ripper 中，规则模式均是常用且命中率较高的恢复模式. 如图2 所示，在使用规则模式进行口令恢复前，用户需要分别指定一个字典文件和一个规则文件. 字典文件中存储了用于规则处理的基础口令；规则文件中存储了以字符串形式表示的规则，一条规则包含了若干规则函数. 随后，口令恢复系统依次从字典文件和规则文件中取出1条输入口令和1 条规则，组合后送入规则变换模块生成待验证口令.

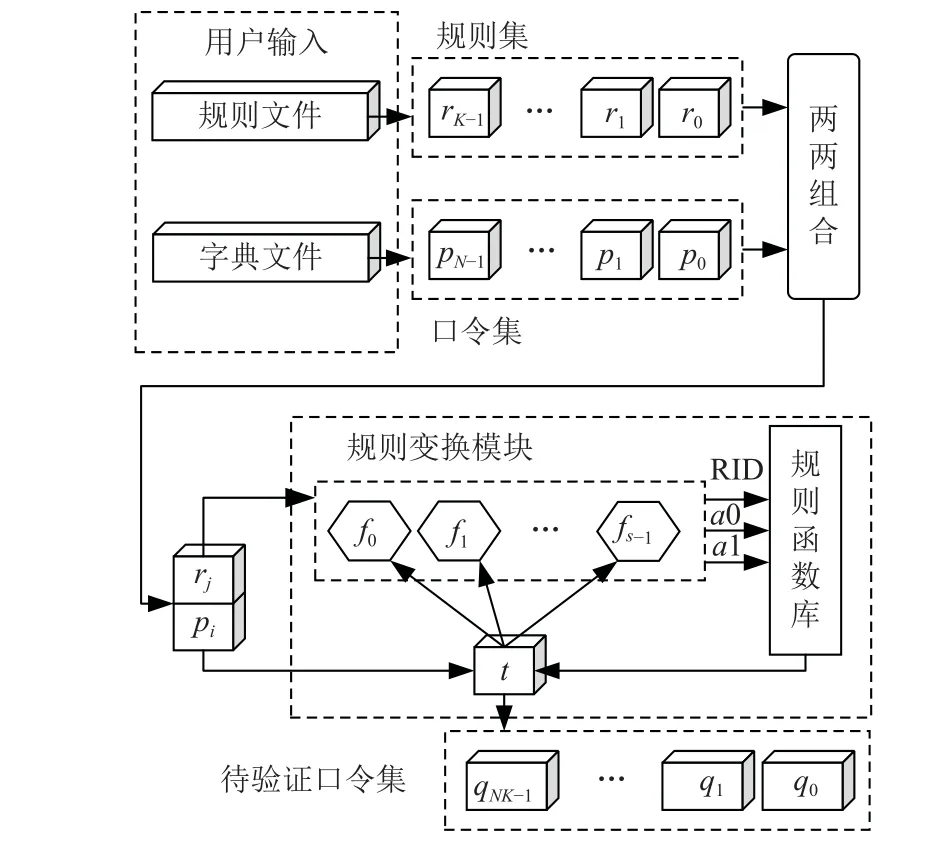
Fig.2 Rule-based password generation process图2 基于规则的口令生成过程

若以集合P={p0,p1, …,pN-1}表示输入口令集，以集合R={r0,r1, …,rK-1}表示规则集，则规则处理过程可以用算法 1 描述，其中对每个“口令-规则”组合（pi, rj）的具体变换过程为：口令生成系统解析当前的规则字符串rj，获取其中的规则函数列表F={f0,f1, …,fs-1}，并令输出口令t = pi，从第1 个规则函数f0开始，依次解析出规则函数的标识符RID 和2 个参数a0，a1，然后根据RID 调用规则函数库中对应的规则函数并传入口令t和参数a0，a1，生成新的口令覆盖t，之后重复对口令t应用剩余规则函数，最后一个规则函数fs-1的输出结果t即为基础口令pi和规则rj生成的待验证口令qi×K+j. 上述过程要求任意一条口令都要和每一条规则组合1 次，因此最终生成的待验证口令数量为基础口令数量N和规则数量K之积.换言之，通过规则处理后一个字典被扩充为原来的K倍.

为了便于区分，后文将对规则集和口令集的处理称为“规则处理”，对“口令-规则”组合的处理称为“规则变换”.

算法1.基于规则的口令生成算法.

输入：输入口令集P，规则集R；

输出：输出口令集Q.

1.4 国内外相关工作

由于申威系列众核处理器主要应用于国产超级计算机系统，所以目前基于申威众核处理器的口令恢复系统研究主要集中在国内. 湖南大学陈玥丹[9]提出了一种神威·太湖之光上的AES 算法的异构并行加速方案，该方案综合利用DMA 技术与并行流水技术实现了高效的AES 算法加解密，相较于串行AES算法减少了89%的执行时间；郑州大学任必晋[1]在太湖之光上实现了PDF，WinZip，NTLM 这3 种算法的口令恢复加速，该方案采取了MPI+Athread 的2级并行实现，并使用DMA 加载切片后的口令，但该方案仅使用了主核生成口令且只实现了掩码模式，因此存在规则模式的性能瓶颈；中原工学院董本松等人[3]基于SW26010 处理器实现了Office 加密算法的优化方案，优化技术包括从核并行、DMA 访存优化、SIMD 向量化等，但该方案中的口令生成部分仍旧为简单的掩码模式；张恒等人[10]研究了SW26010处理器上MD5 算法的优化技术，但同样仅使用了掩码模式生成口令. 可以看到，当前基于申威系列众核处理器的口令恢复研究均未涉及诸如规则处理等更复杂的口令生成方法，因此现有口令恢复系统在规则模式下的性能难以满足需求，亟需对规则处理进行优化.

在其他处理器平台方面，Hashcat[5]是目前主流的基于GPU 的口令恢复工具，为了解决CPU 口令生成速度瓶颈问题，Hashcat 在GPU 上实现了掩码和规则2 种口令生成算法内核，使得口令生成和口令验证均在GPU 核心上完成，从而避免了大量的口令数据传输并且提高了口令生成速度，但Hashcat 的规则函数实现专门针对GPU，在申威处理器上的执行效率不高；谢鑫君等人[11]提出了一种基于GPU 的对口令进行穷举的技术，该技术本质上与基于掩码的口令生成类似，通过GPU 多线程加速，将口令生成速度相较于CPU 提升了4 个数量级；郑州大学董婉莹[12]提出了一种基于口令字典树的口令生成方法，该方法通过统计口令字符的频率构建字典树，然后基于字典树生成掩码，最后利用掩码生成口令，该方法还采用FPGA 对掩码生成口令的过程进行了加速，实现了平均12.85 倍的加速比.Zhang 等人[13]基于FPGA 提出了一种专用规则处理加速器（RUPA），解决了CPUFPGA 异构口令恢复系统的口令生成瓶颈，使系统性能提升了245.4 倍.

在使用规则进行口令生成的研究中，Weir 等人[14]较早地提出使用概率上下文无关文法(probabilistic context-free grammars, PCFG)学习公开口令集的分布特征从而生成规则集，消除了传统规则集设计需要依赖人工专家的弊端；Marechal[15]提出的rulesfinder工具和Kacherginsky[16]提出的PACK 工具，能够利用机器学习自动产生规则集；Nam 等人[17]利用对抗生成网络方法产生了REDPACK 规则集，使规则处理的猜测命中率提升了至多26%；Li 等人[18]提出了一种基于密度聚类的规则生成方法，所生成的规则集的猜测命中率提升了104%. 经过不断的研究和探索，目前规则处理已经成为Hashcat 和John the Ripper 中最高效的口令恢复模式，其猜测命中率接近神经网络的同时，生成速度可达到神经网络的10 倍以上[19-20].

2 规则处理算法的可并行度分析

2.1 线程级可并行度

线程级并行优化的前提是将计算任务分解为若干相对独立的子任务，通过图2 可知，在规则处理过程中，一对“口令-规则”组合是其最小的处理单元，且任意“口令-规则”组合的规则变换过程互不干涉，因此可以将一次规则变换作为一个子任务. 尽管一次规则变换中还包括了若干次规则函数的调用，但这些调用之间存在次序关系，因此子任务不能继续细分到规则函数层次. 结合图2 分析，若口令集P和规则集R的大小分别为N和K，则规则处理算法的总任务数量为N×K，假设不同子任务具有相同的运算时间w，则规则处理算法在串行处理器上的执行时间为Ts=N×K×w. 由于规则处理算法的各个子任务互相独立可以完全并行执行，根据Amdahl 定律[21]，其在并行处理器上的执行时间为Tp=N×K×w/C，其中C为并行处理器的最大线程数，因此规则处理算法的线程级可并行度为Ts/Tp=C，在SW26010 处理器单个核组上的最大加速比为64.

2.2 数据级可并行度

规则处理算法经过分解成为规则变换子任务后，每个处理器核心需要依次完成属于自己的子任务.在单个处理器核心中，规则变换子任务之间已经无法并行. 而规则变换本质上是对口令应用规则函数，因此规则函数是规则变换的核心与关键，规则函数的性能也决定了规则变换的性能. 为了提升规则变换子任务的执行效率，还需要探索规则函数的数据级可并行度. 在Hashcat 和John the Ripper 中常用的规则函数有41 种，这些规则函数数量众多且类型繁杂，有必要针对其计算特点进行分类讨论.

根据1.3 节的分析，规则函数的输入为口令p和2 个参数a0，a1，输出为口令q，其C 语言应用程序编程接口（application programming interface, API）如图3所示. 在现有实现中，输入口令p通过长度为N的字符数组p[N]储存，输出口令通过字符数组q[N]存储，N的取值决定了口令恢复系统能够处理的最大口令长度，通常取N=32.此外，口令恢复系统从字典文件中加载口令时会单独计算出口令的长度L，和数组p[N]一起存放于口令结构体pwd_t中，为了提高口令的传输效率，口令结构体中定义了额外的3 个占位符以保证其内存占用为4 B 的整数倍. 参数a0，a1 主要为部分带有可变参数的规则函数提供额外的信息，根据规则函数的不同，其意义也会产生变化，部分规则函数没有可变参数，此时a0，a1 的取值对函数执行结果无影响.

Fig.3 The unified C-language API of rule functions图3 规则函数的C 语言统一应用程序编程接口

根据函数内部对字符数组p[N]的计算模式，规则函数可分为5 类：

1） 全字符遍历变换

全字符遍历变换（operation on all characters，OAC）函数的计算模式伪代码如图4 所示.OAC 函数中输出口令与输入口令长度相同，输出字符q[i]是与其位置相同的输入字符p[i]，a0 和a1 的函数ROP（p[i]，a0，a1），这里函数ROP泛指包括大小写转换、数值加减、移位等操作在内的各种变换函数.OAC 类型函数包括lowercase，uppercase，toggle等.

Fig.4 The computing pattern of OAC-type functions图4 OAC 类型函数的计算模式

2） 指定字符变换

指定字符变换（operation on specified characters，OSC）函数的计算模式伪代码如图5 所示. 与OAC 函数类似，OSC 函数的输出口令长度与输入口令长度相同，但只有输出字符q[a0]是输入字符p[a0]的ROP变换，其余位置的输出字符与输入字符相同.OSC 类型函数包括overwrite，toggle@等.

Fig.5 The computing pattern of OSC-type functions图5 OSC 类型函数的计算模式

3） 全字符遍历移动

全字符遍历移动（move across all chacracters，MAC）函数的计算模式伪代码如图6 所示.MAC 函数的输出口令长度L_new与输入口令长度L不一定相同，L_new的值由L，a0，a1 共同决定，每一个输出字符q[i]由某个输入字符p[idx]直接移动得到，p[idx]的位置坐标idx通过CalcIndex（i，L）计算得到.MAC 函数包括reverse，duplicate等.

Fig.6 The computing pattern of MAC-type functions图6 MAC 类型函数的计算模式

4） 指定字符移动

指定字符移动（move across specified characters，MSC）函数的计算模式伪代码如图7 所示. MSC 函数的输出口令长度L_new同样取决于L，a0，a1，但只有输出字符q[a0]和q[a1]由其他位置的输入字符p[idx]直接移动得到，其余位置的输出字符与输入字符相同. MSC 函数包括swap_front，swap_back，replace_N+1 等.

Fig.7 The computing pattern of MSC-type functions图7 MSC 类型函数的计算模式

5） 指定字符清除

指定字符清除函数purge是单独成类的一个规则函数，其计算模式与前面4 种函数有较大差异，如图8 所示. 函数purge的功能是去除口令p[N]中ASCII 值等于a0 的所有字符，留下其余的字符作为输出字符. 这种情况下，尽管输出字符q[i]仍由某个输入字符p[idx]直接移动得到，但p[idx]的位置坐标idx无法通过i和L直接计算，而是与输入字符的ASCII值p[0]，p[1]，…，p[N-1]有关，因此必须依次读取并比较所有输入字符的值才能最终确定输出字符.

Fig.8 The computing pattern of the purge function图8 函数purge 的计算模式

上述5 类规则函数的主体部分均为一个for 循环，循环次数为输入口令长度L或输出口令长度L_new，除函数purge外，OAC，OSC，MAC，MSC 函数中的for循环体之间均无依赖关系，因此各循环体理论上可以完全并行执行，其数据级可并行度为L或L_new.然而现有规则函数实现方案无法发挥SW26010 处理器从核核心的数据级并行能力，这是因为每个从核核心只具有1 条整数流水线和1 条256 b 的SIMD 流水线，现有规则函数实现方案只能利用其中的整数流水线达成每条指令处理4 个字符，而无法利用256 b 的SIMD 流水线.

3 线程级并行优化技术

3.1 主从核任务分配机制

SW26010 处理器的一个核组主要由1 个主核与64 个从核构成，其中主核适合复杂逻辑运算和I/O 操作，从核适合相对简单但可并行的运算，主核、从核需要合理的分工才能发挥各自的性能优势. 图9 展示了本文提出的规则处理系统的主从核任务分配机制，图中的处理器系统被简化为主核、从核阵列和主存3 个部分. 其中，主核负责解析输入参数，根据输入参数从硬盘中读取字典文件和规则文件，并对字典文件和规则文件进行预处理，生成口令数组、规则数组以及口令数量、规则数量等参数，然后启动从核阵列进行规则变换；从核阵列主要负责处理规则变换子任务，根据主核生成的参数，每个从核找到自己对应的子任务集然后执行规则变换，规则变换生成的输出口令集存储于LDM 中，供后续口令验证任务使用.

Fig.9 Task assignment policy of the master core and the slave core图9 主从核任务分配机制

3.2 子任务映射机制

在线程级并行优化中，如何将规则变换子任务映射到众核处理器的各个从核是首先要解决的问题.根据2.1 节所述，大小分别为N和K的口令集和规则集组合成的子任务集大小为N×K，此处暂时假定所有子任务的运算量相同，按照规则处理的流程，需要将子任务集划分为64 等份分配给64 个从核，其中每份的子任务数量为N×K/64.为实现子任务集的划分，一般有共用口令映射（share passwords mapping, SPM）和共用规则映射（share rules mapping, SRM）两种方案，如图10 所示. 在共用口令映射方案中，规则集R被均匀划分为64 个子集R0，R1，…，R63，分别分配给从核0、从核1、…、从核63，而口令集则不经划分直接分配给所有从核. 与之相反，共用规则映射方案中，口令集被均匀划分并分配给64 个从核，规则集则不划分.

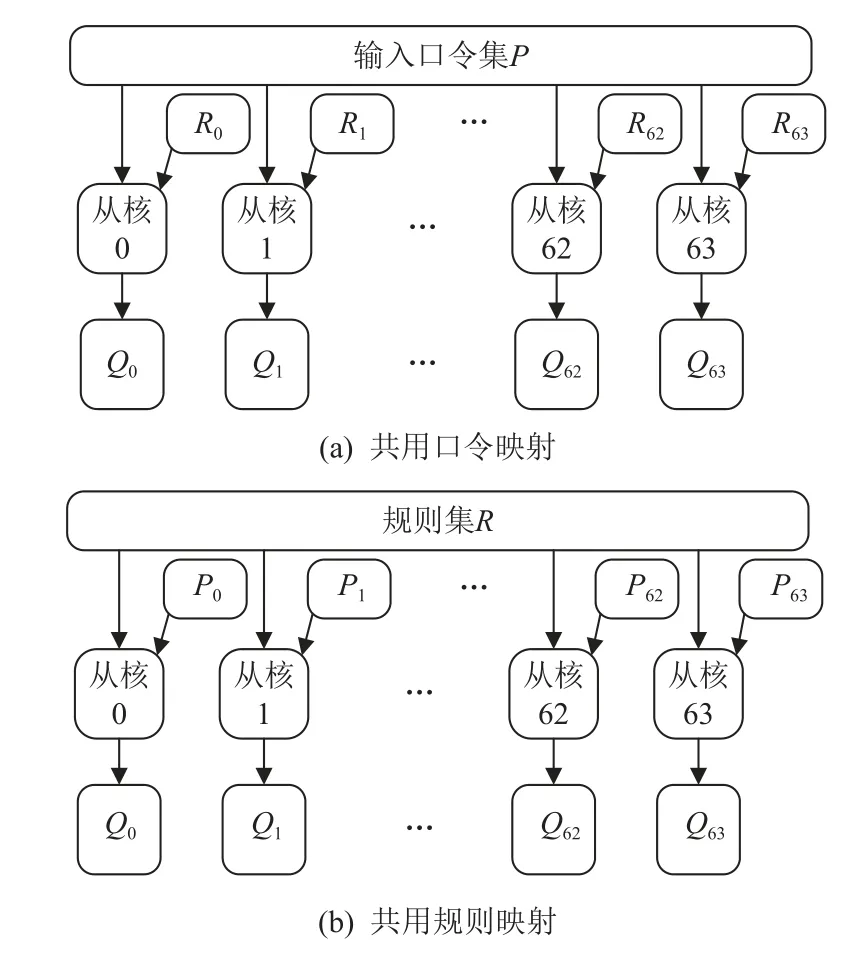
Fig.10 Sub-task mapping scheme of slave cores图10 从核子任务映射方案

在规则处理的过程中，由于从核的局存不能存储完整的口令集和规则集，因此必须以分块的方式进行加载. 口令和规则的加载也有2 种方案：一种是口令外循环-规则内循环（password-out-rule-in, PORI），即在外部循环中读取口令分块，在内部循环中读取规则分块；另一种则是口令内循环-规则外循环（passwordin-rule-out, PIRO）. 任务映射方式和数据加载方式两两组合能够得到4 种方案，分别为SRM-PORI，SRM-PIRO，SPM-PORI，SPM-PIRO.

任务映射方式和口令规则加载方式主要影响了从核阵列整体与主存间的数据通信量，若每条口令数据大小为u字节，每个口令块包含x条口令，每条规则数据大小为v字节，每个规则块包含y条规则，则以上4种方案下核组的总数据通信量可由式（1）近似计算：

由式（1）可以看出

因此在PORI 方案下使用SRM 映射的数据通信量更小，在PIRO 方案下则应该使用SPM 机制，而WSRM-PORI与WSPM-PIRO的大小关系则与N，K，u，v，x，y的具体取值有关，后文若无特别说明，默认基于SRMPORI 方案展开讨论.

3.3 从核缓冲区配比优化机制

SW26010 处理器中每个从核具有64 KB 的LDM，利用好局部缓存提升从核的数据访问效率同样是并行优化的关键. 在规则处理算法中，输入口令集P、规则集R，以及生成的输出口令集Q都需要一定的存储空间. 通常情况下，上述3 个集合占用的空间均远大于从核的局部缓存空间，因此必须对输入口令集P、规则集R、输出口令集Q进行分块读取和写入，这里不妨将它们对应的局部缓冲区称为P 缓冲、R 缓冲和Q 缓冲，优化P，R，Q 这3 种缓冲区的容量配置能够减少从核对主存的数据访问量，提升规则处理访存性能和降低访存能量消耗.

为了分析有限LDM 空间下P，R，Q 这3 种缓冲区容量的最佳配比，首先需要介绍本文提出的从核规则处理任务执行机制，如算法 2 所示. 首先每个从核使用系统调用函数GetSlaveCoreID获得自己的从核ID 号cid（cid= 0，1，…，63），然后根据cid和任务映射机制M计算从核需要处理的口令集和规则集的起始位置和大小. 共用口令映射时口令集的起始位置p_idx= 0，口令集大小n=N， 规则集的起始位置r_idx=K×cid/64，规则集大小k=K/64；共用规则映射时p_idx=N×cid/64，n=N/64，r_idx= 0，k=K. 确定从核需要处理的口令集和规则集后，从核进入一个双重循环，在外循环（口令循环）中从核每次加载x条口令到P 缓冲中，然后执行内循环（规则循环），在内循环中，从核每次加载y条规则到R 缓冲中，然后对P缓冲和R 缓冲中的口令子集和规则子集进行处理，生成的输出口令子集存储于Q 缓冲中，用于后续口令验证过程，不写回主存.

算法2.从核规则处理任务执行机制.

输入：输入口令集P，规则集R，映射机制M；

输出：是否破解成功cracked.

①cid←GetSlaveCoreID（）；

②p_idx，n←GetMyPasswordSet（M，cid）；

③r_idx，k←GetMyRuleSet（M，cid）；

④i← 0；

⑤ whilei＜ndo

⑥Pbuf←DMALoadPassword（P，p_idx+i，x）；

⑦j← 0；

⑧ whilej＜kdo

⑨Rbuf←DMALoadRule（R，r_idx+j，y）；

⑩cracked←RunRuleProcess（Pbuf，Rbuf）；

⑪j←j+y；

⑫ end while

⑬i←i+x；

⑭ end while

⑮ returncracked；

⑯ procedureRunRuleProcess（Pbuf，Rbuf）

⑰cracked← 0；

⑱s← 0；

⑲ fori= 1 →xdo

⑳ forj= 1 →ydo

㉑Qbuf[s]←ApplyRule（Pbuf[i]，Rbuf[j]）；

㉒s←s+ 1；

㉓ ifs=zthen

㉔cracked←PasswordValidate（Qbuf）；

㉕s← 0；

㉖ end if

㉗ end for

㉘ end for

㉙ ifs＞ 0 then

㉚cracked←PasswordValidate（Qbuf）；

㉛ end if

㉜ returncracked；

㉝ end procedure

下面首先考虑算法 2 中单个从核与主存间的数据通信量和通信时间. 设每条口令占用的存储空间为u字节，每条规则占用的存储空间为v字节，于是口令循环的循环次数为「n/x」，每次循环读取的口令数据量为ux；规则循环的循环次数为「k/y」，每次循环读取的规则数据量为vy；因此算法 2 中口令数据总读取量为WP=ux×「n/x」、规则数据总读取量为WR=vy×「k/y」×「n/x」. 由于输出口令集Q不会被写回主存，Q 缓冲的大小不影响数据通信量和通信时间，所以参数z未出现在WP和WR的表达式中. 尽管WP和WR的表达式中所有变量均为自然数，为了简化分析，后文中将其取值范围定为[1, +∞），即不小于1 的实数.

在算法 2 中，从核使用DMA 技术与主存进行数据传输，DMA 读写数据的开销可以分为两部分：一部分是DMA 启动的固定开销D；另一部分是随传输数据量线性增加的数据传输开销g. 因此算法 2 中数据传输的总时间T可以用式（3）计算. 由于大多数情况下有n≫x和k≫y，并且程序会自动调整最后一轮循环加载的数据量，因此式（3）中的向上取整符号可以近似忽略.

根据需要分析的参数不同，式（3）有不同的诠释方法，显而易见的有：

1） 口令集和规则集越大，则n和k越大，通信时间T越大；

2） DMA 的传输速率越大、固定开销越小，则g和D越小，通信时间T越小；

3） 单条口令和规则的存储空间越小，则u和v越小，通信时间T越小.

当研究给定口令集和规则集下的最佳P 缓冲和R 缓冲配比（即x和y的取值）时，式（3）中u，v，k，n，g，D可以视为常数，并且P 缓冲、R 缓冲、Q 缓冲的总容量大小受从核LDM 大小限制，x、y还应满足ux+vy≤S，其中S为除去Q 缓冲外可用于缓冲的LDM空间大小. 因此数据通信时间T的最小值计算可转化为一个非线性优化问题，如式（4）所示. 对式（4）求解可得式（5）.

通过实际测试SW26010 中从核DMA 的性能，测得式（5）中g≈ 2.069×10-9s/B，D≈ 5.172×10-7s. 此外，通常单条规则数据大小4 ≤v≤128，规则数量k＞ 100，据此可计算出式（5）中

由于1/kv≪1/40，该项可忽略不计，因此式（5）中x*和y*几乎不随k的取值发生变化. 换言之，P 缓冲、R 缓冲大小的最佳配比与口令集大小n和规则集大小k均无关. 根据这一结论，设计程序时可以结合实际可用的LDM 空间计算最佳的P 缓冲、R 缓冲大小，从而减少从核阵列与主存的通信时间和通信量.

3.4 口令规则数据结构优化技术

式（3）揭示了从核数据通信时间T与口令数据大小u和规则数据大小v正相关，因此减小口令数据大小和规则数据大小能够降低从核数据通信开销.在现有实现中，每条口令采用36 B 存储，每条规则采用128 B 存储，其C 语言结构体如图11 所示. 其中每个规则结构体rule_t由一个数组rfs[32]构成，数组rfs[32]中的每个元素为一个规则函数结构体，每个规则函数结构体包括了函数名称（name）、参数0（a0）、参数1（a1）和占位符（pos），每个规则结构体可存储的规则函数最多为32 个.

Fig.11 Data structure of the password and the rule图11 口令与规则的数据结构体

图11 中口令和规则的结构体的定义方式不能充分利用从核的LDM 空间. 首先口令结构体为了保持4 B 对齐以提高传输效率，浪费了3 B 的空间作为占位符，对此，本文将口令结构体中的最大口令长度N设置为31，并去除了占位符，从而在保持4 B 对齐的情况下将口令结构体缩小为32 B，考虑到绝大部分正确口令长度小于16 B，将最大口令长度减少1 B 的影响可以忽略不计.

另一方面，规则结构体中固定包含32 个规则函数结构体，然而实际使用的规则中包含的规则函数数量平均为3 个左右，因此按照图11 中的定义方式平均浪费了90.6%的空间. 为了解决这一问题，本文提出了变长规则存储机制，如图12 所示展示了2 条相邻的规则“uT2”和“Cp2$AsAB”，其中规则“uT2”由规则函数“u”和“T2”组成，规则“Cp2$AsAB”由规则函数“C”“p2”“$A”“sAB”组成. 注意到每个规则函数使用4B 存储，在原定义方式下第4 个字节为占位符，而在变长规则存储机制中，第4 个字符为规则结束指示符. 当指示符为0 时，表示当前规则后面还有其他规则函数，当指示符为1 时表示当前规则结束. 通过变长规则存储机制，图12 中2 条规则需要的存储空间由256 B 降至24 B.

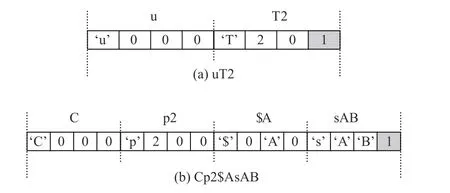
Fig.12 Variable length rule storage policy图12 变长规则存储机制

3.5 从核间负载均衡机制

3.1～3.4 节的分析假定了规则处理算法的各个子任务具有相同的运算复杂度，然而在实际中，不同子任务的运算复杂度往往是不同的，差异来源主要有3 个方面：一是不同规则包含不同数量的规则函数，一般而言规则函数越多运算复杂度越大；二是不同规则函数的运算复杂度不同，例如函数append（“$X”）只需在口令最后添加一个字符X，而函数lowercase则需要遍历口令中的所有字符，判断其大小写状态并对其修改；三是同一规则函数在处理不同口令时运算复杂度不同，例如函数lowercase在处理8 B 长度的口令时需要至少8 次运算，而处理16 B 长度的口令时需要至少16 次运算.

在当前规则处理方案中，子任务在从核间按照数量均匀分配，由于并行处理器每个核心的运算能力相同，若各个核心分配到的子任务总运算复杂度差异较大则会导致部分核心提前于其他核心完成任务，从而处于空闲状态，浪费了算力导致加速比下降.对此一种朴素的解决方案是提前计算出各个子任务的执行时间，进而依照子任务的执行时间在核心间均匀分配，但是口令集和规则集的随机性以及计算子任务时间的开销使得这种方案不可行.

为了解决这一问题，本文设计一种从核间负载均衡机制，其原理如图13 所示. 主核从字典文件中加载口令时计算出输入口令的总数量，并将输入口令集分为大小均为m的子集，然后在主存中设置一个信号量s记录待处理的子集总数量. 处理开始后，每个从核依次读取主存中的信号量s，并将其减1 然后更新s. 这一过程采用原子操作进行，避免多个从核同时更新s而发生错误. 之后根据s的值计算需要处理的口令的起始地址并对其执行规则处理.

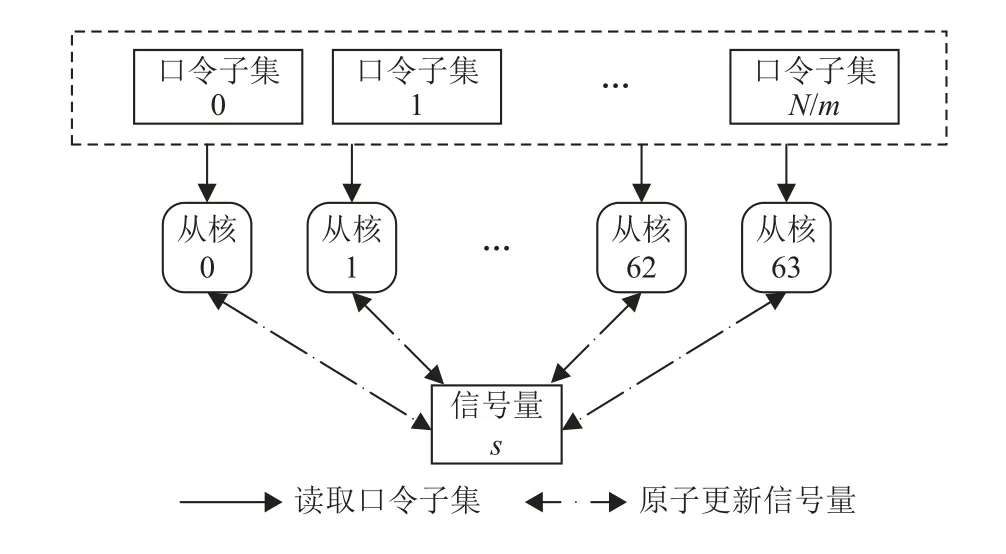
Fig.13 Workload balance policy between slave cores图13 从核负载均衡机制

图13 所述的负载均衡机制可以使不同从核的处理时间的极差不超过m条口令的处理时间. 因此若要尽可能减小不同从核的处理时间差异，则需使m的取值尽可能小. 但是当m很小时，从核会频繁地对信号量s进行原子更新操作，考虑到从核对主存的访问开销，整体的规则处理时间反而会增大. 实践中应综合考虑上述因素的影响选取最佳的参数设置.

4 数据级并行优化技术

数据级并行优化技术主要针对单次规则函数的执行过程，2.2 节以字符为单位分析了各类规则函数的数据级可并行度，对绝大部分规则函数，理想情况下每个字符的处理都可以完全并行，然而以字符为单位进行处理意味着从核中每条指令最多处理1 个字符，而SW26010 中从核最多可以同时执行2 条指令，因此以字符为单位的处理方式在从核上的执行时可并行度最多为2.尽管在Hashcat 中对规则函数进行了优化，将4 个字符当作一个32 b 的无符号整型数据进行了处理，使得部分规则函数的性能得到了提升，但这种优化仍然不能充分发挥SW26010 处理器从核的性能. 一方面每条指令最多只能处理4 个字符，不能充分利用从核中向量寄存器256 b 的位宽；另一方面部分规则函数的实现未能高效利用申威SIMD 指令集中的特殊指令，无法达到最佳优化效果.

为了进一步提升规则函数的执行效率，本文提出了基于申威SIMD 指令集的规则函数优化方案，该方案的核心是通过合理使用SIMD 指令，降低执行规则函数需要的指令数量，进而降低规则函数的执行时间. 使用SIMD 指令实现规则函数的基本思路是将输入口令存储于SIMD 向量寄存器中，利用SIMD 指令对口令中的多个字符同时进行相同的操作，最后将SIMD 向量寄存器中的输出口令写回主存. 根据2.2 节中的分析，现有的41 种规则函数可以分为OAC，OSC，MAC，MSC 这4 种类型和函数purge. 除单独的规则函数purge较为特殊外，其余4 类规则函数均有明显的计算访存特征，因此相应的SIMD 实现也围绕其计算访存特征展开.

1） 对于OAC 类型规则函数，其特点为对所有输入口令字符的操作完全相同且互不依赖. 互不依赖的特性决定了对每个字符的操作可以完全并行，对所有输入口令字符的操作完全相同决定了这些操作可以用完全相同的指令完成，这一特点非常契合SIMD指令的设计思路，所以对OAC 类型函数直接使用SIMD 指令将其并行化即可得到很好的加速效果.

2） 对于OSC 类型规则函数，其特点在于只对特定位置的1 个字符采取操作，其余位置字符保持不变. 由于申威SIMD 指令集不支持单独对SIMD 向量中的1B 进行操作，所以OSC 类函数必须结合掩码实现，即首先生成一个待处理字节位置全为“1”、其余位置全为“0”的掩码，然后对原口令向量中所有字符进行相同操作生成新口令向量，最后根据掩码组合的原口令向量与新口令向量得到输出口令向量. 组合方式为：掩码为“1”的位置使用新口令向量的值，掩码为“0”的位置使用原口令向量的值.

3） 对于MAC 类型规则函数，其特点为对所有字符采用特定的方式进行位置变换. 在以字符为单位的处理方式中，对每个字符直接进行位置变换都会产生1 次读操作和1 次写操作，要生成长度为L的输出口令则会产生2L次读/写操作，带来可观的时间开销. 要提升此类函数的性能就必须尽量减小读/写操作的数量，申威SIMD 指令集中提供了向量移位指令和向量混洗指令，利用这2 类指令可以在SIMD 向量中同时变换多个字符的位置，并且无需读写存储器.

4） 对于MSC 类型规则函数，其特点为对特定的1 个或2 个字符进行位置变换. 由于申威SIMD 指令集不支持对SIMD 向量中的单个字节进行移动，所以要实现MSC 类型函数同样需要结合掩码，即首先生成目标字节位置处的掩码，然后对原口令向量中的所有字符进行移动生成新口令向量，最后通过掩码组合原口令向量与新口令向量得到输出口令向量.

5） 对于函数purge，由于对其各个字符的操作之间存在数据依赖，因此难以使用SIMD 指令实现，本文仍旧采用普通标量指令集对其进行实现.

在上述SIMD 优化思路的基础上，本文提出了4种SIMD 优化方案.

4.1 口令数据向量化

在2.2 节规则函数实现中，口令数据以结构体方式存储，每条口令占据32 B 存储空间. 为了使用SIMD 指令进行规则函数实现，必须首先将口令数据加载到SIMD 向量寄存器中，由于SW26010 的向量寄存器位宽为256，因此恰好能够存放1 条口令. 将口令数据加载到向量寄存器时，位置靠前的字符被存储于向量寄存器的低位，例如p[0]存储于向量寄存器的第0～7 位，p[1]存储于向量寄存器的第8～15 位，以此类推. 口令数据向量化的优势和劣势并存. 其优势在于对口令中字符的所有操作均在寄存器中进行，避免了存储读写；其劣势在于将口令数据加载到向量寄存器以及将向量寄存器中的口令数据写回LDM 的过程会带来额外的开销. 口令数据的加载开销可以通过多次复用输入口令进行均摊，而口令数据的写回开销则无法避免.

4.2 大小写转换向量优化

大小写转换是规则函数中出现频率最高的一类ROP变换操作，在41 种常用的规则函数中，使用到大小写转换的规则函数共有8 种，分别为lowercase，uppercase，capitalize，invert_capitalize，toggle，toggle@N，title，title_w/separator. 通常大小写转换的实现采用条件分支语句，如图14 所示，首先判断字符c为大写字母还是小写字母，若为大写字母则将其ASCII 值加32，若为小写字母则将其ASCII 值减32.这种实现方式存在2 个弊端，首先条件运算会导致同一口令中的不同字符可能具有不同的执行分支，这将破坏SIMD 指令的应用条件，使其无法使用SIMD 指令加速；其次申威SIMD 指令集中不包含8b 向量加/减法指令，若以32b 向量加/减法指令实现“c+32”和“c-32”语句则每条指令最多只能同时处理8 个字符，降低了执行效率.

Fig.14 Toggle case function图14 大小写转换函数

本文对大小写转换函数的优化实现如图14 中的函数opt_toggle_case所示. 其基本原理为互相对应的大写字母与小写字母的ASCII 值相差固定为32.在二进制角度，大写字母与小写字母的ASCII 值仅第5 位不同，大写字母的第5 位为“0”，小写字母的第5 位为“1”，因此将任何小写字母的ASCII 值与“0x20”异或即可得到其对应的大写字母的ASCII 值，反之亦然. 但在此之前，必须先保证输入字符c是大写字母或小写字母，函数opt_toggle_case中展示的方法可以筛选出ASCII 码在[64, 128）区间内且低5 位在[1, 26]区间内的字符，满足此条件的字符即为大写字母或小写字母. 将满足条件的字符与“0x20”异或即可完成大小写转换. 此方法不会产生条件分支语句，因此可以直接向量化，如函数opt_toggle_case_vector所示.

4.3 字符匹配向量化

在OAC 类型规则函数中，replace（“sXY”），title（“E”）和title_w/separator（“eX”）是较为特殊的3种函数. 其他OAC 类型规则函数（例如lowercase）对所有字符执行同样的ROP操作，而这3 种函数则只对特定ASCII 值（假设为X）的字符执行ROP操作，因此必须首先找到ASCII 值为X的字符的位置. 在传统实现方案中，这一字符匹配的过程只能通过依次遍历输入口令中的每个字符实现. 本文使用SIMD 指令对字符匹配进行了向量优化，如图15 所示为函数replace向量优化前后的代码. 由于申威SIMD 指令集中不存在以8 b 字符为基本元素的比较指令，因此必须将一个32 b 整型数的4 B 分开比较. 经过simd_veqvw指令同或操作后，口令中所有ASCII 值等于X的字符均会变为“0xff ”. 然后保留值为“0xff ”的字节并将其他字节置为0 形成掩码，最后通过此掩码进行字符替换.

Fig.15 Vector optimization of the replace function图15 函数replace 的向量优化

4.4 基于向量移位指令的优化

在MAC 和MSC 类型规则函数中存在很多向输入口令中增加或减少字符的函数，例如函数delete删除口令中的第1 个字符，函数insert向口令的第N个字符位置插入字符M，这些函数均需要对输入口令中的全部或部分字符进行移动. 在传统的以单个字符为基本操作单元的实现中，移动一个字符需要4个步骤：计算源字符坐标、计算目的字符坐标、读取源字符、写入目的字符. 对多个字符进行这4 个步骤会产生大量的读写指令. 值得注意的是这类函数中对字符的移动存在规律性，即所有字符的移动方向和步长是相同的，因此可以通过整体移动进行优化.

SW26010 处理器提供了一类向量移位指令，该类指令可以同时移动256b 向量中的32 个字符，以函数truncate_left为例，图16 展示了其SIMD 优化前后的代码. 原本需要L_new次的字符移动操作利用simd_srlow指令只需要1 条指令即可完成，提高了函数执行效率. 其他类似的规则函数也可以利用向量移位指令实现并行优化，例如函数rotate_left，rotate_right，insert，prepend等，篇幅所限此处不再赘述.

Fig.16 Vector optimization of the truncate_left function图16 函数truncate_left 的向量优化

4.5 基于向量混洗的优化

在MAC 和MSC 类型函数中还存在若干改变输入口令字符位置的函数，例如函数reverse，reflect，duplicate_all，这些函数不同于4.4 节中增加或减少字符的函数，其字符移动的方向和步长不统一，因此无法单纯通过向量移位指令实现. 对这些规则函数的向量优化利用了SW26010 处理器中的向量混洗指令simd_vshuffle，该指令能够将向量寄存器中的8 个32 b整型数据以任意顺序重新排列，以函数reverse为例，图17 展示了使用向量混洗指令优化前后的代码.

Fig.17 Vector optimization of the reverse function图17 函数reverse 的向量优化

5 实验评估

为了评估各项优化技术的实际效果，本文基于神威·太湖之光超级计算机设计了实验，实验中使用了单个核组硬件资源，其参数如表2 所示.

Table 2 Hardware Resource Configuration of a Single Core Group in SW26010 Processor表2 SW26010 处理器单核组硬件资源配置

在表2 所示的硬件平台上，本文测试了不同口令恢复系统架构和规则函数实现版本下的系统性能指标，各种系统架构和规则函数实现的可选项如表3所示. 系统架构方面，本文测试了主核处理（MASTER）和从核加速（SLAVE）这2 种规则处理方案；规则函数实现方面，本文测试了不同版本的规则函数实现代码，其中CWISE 每条指令处理1 个字符，OPT32为Hashcat 中实现的版本，每条指令处理4 个字符. 为了表述方便，后文以“口令恢复系统架构-规则函数实现版本”组合表示一种具体的配置，例如“SLAVESWV”表示采用从核进行口令生成，规则函数实现针对申威SIMD 指令集进行了优化. 测试程序使用sw5cc进行编译，版本号为“5.421-sw-500”，编译优化级别为“O2”. 实验中的性能指标通过读取SW26010 处理器中的实时时钟计数器并换算得到.

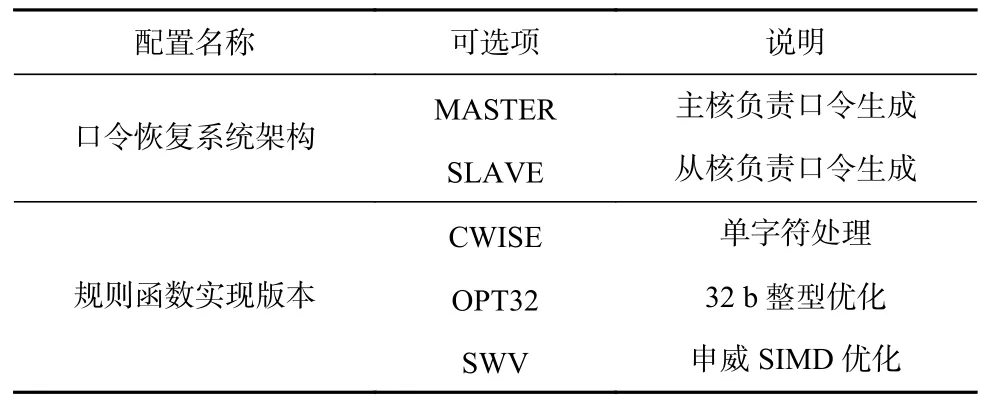
Table 3 Configurable Arguments of the Benchmark Program表3 测试程序可配置参数

实验选取了5 个具有代表性的Hashcat 规则集作为测试规则集，分别为best64，d3ad0ne，dive，rockyou-30000，unix-ninja-leetspeak.其中best64 是最常用的规则集，d3ad0ne 中包含了多个函数purge，dive 是最大的规则集，rockyou-30000 不包含函数purge，unix-ninjaleekspeak 只包含OAC 和OSC 类型规则函数，且规则长度较大.

5.1 并行任务映射机制

表4 列出了4 种映射机制方案下单个从核的数据通信时间、数据通信量和DMA 次数. 实验中P 缓冲、R 缓冲、Q 缓冲的大小分别为16 KB，16 KB，4 KB，口令集数量为64 万条，规则集数量为16 384 条，单条规则采用128 B 存储. 由表4 中数据可以看出，在当前实验设置下，SPM-PIRO 方案具有最小的数据通信量和最小的数据通信时间，但与SRM-PORI 和SRM-PIRO 这2 种方案差距不大，而SPM-PORI 方案的数据通信量和通信时间最大，这是因为SPM 映射下从核需要处理的口令数量最多，使得口令外循环的次数增多，进一步导致规则内循环的次数增加，通过口令和规则分块的DMA 传输次数可以验证这一结论，因此在口令数量远多于规则数量的情况下，应该避免采用SPM-PORI 方案.

Table 4 Comparison of Communication Overhead of a Single Slave Core under Different Task Mapping Policies表4 不同任务映射机制下单个从核的通信开销比较

5.2 从核缓冲区配比优化机制

为了验证从核缓冲区配比优化机制的效果，本文实验测试了最优策略、等容量策略、等数量策略这3 种不同的缓冲区分配策略下的数据通信时间与通信量，其中最优策略依据式（5）计算得出，等容量策略将P 缓冲和R 缓冲设置为相同容量，等数量策略令P 缓冲和R 缓冲中存储的口令和规则数量相等.实验中使用的口令集大小为64 万条，规则集大小为16 384 条. 在测试最优策略的性能时，实验还选取了与理论最优缓冲区配置相近的其他配置以验证理论最优是否为实测最优，实验结果如图18 所示.

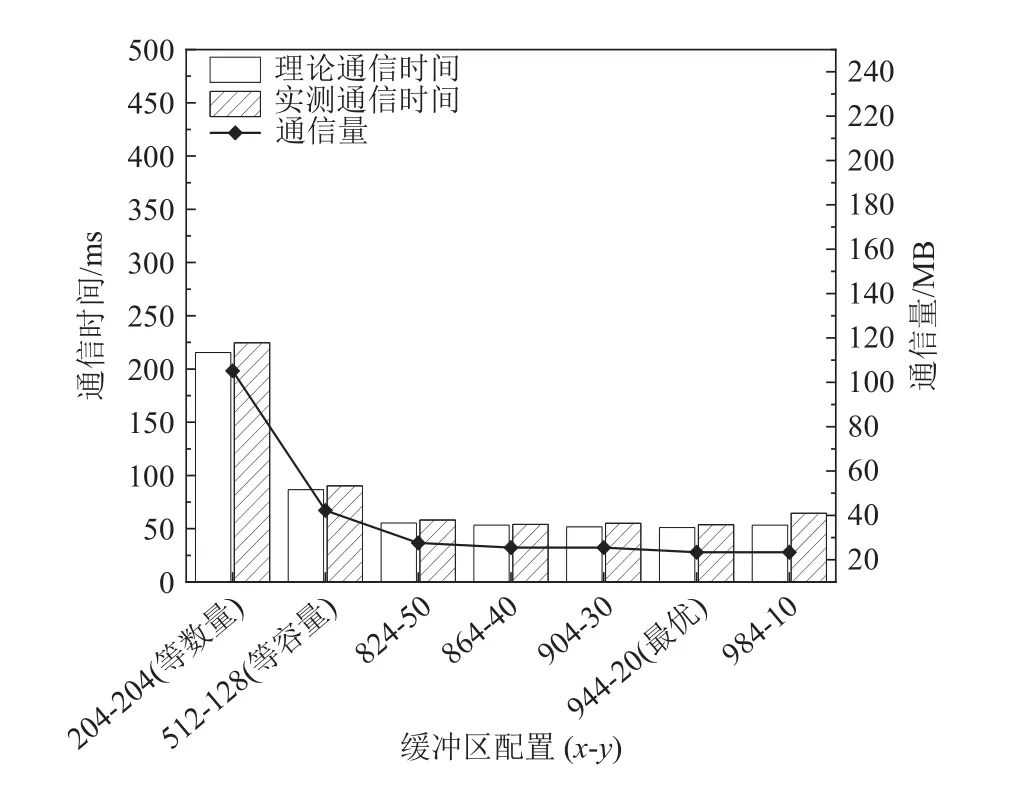
Fig.18 Communication overhead under different buffer sizes图18 不同缓冲区大小下的通信开销

图18 中使用的缓冲区总容量S为32 KB，单条规则数据v大小为128 B，此时式（5）计算得到的最优P 缓冲口令条数x*约为944，最优R 缓冲规则条数y*约为20，而在“944-20”配置下的实测通信时间同样也取得了最小值，说明理论结果与实测结果吻合，验证了3.3 节中数据通信时间模型的准确性. 相比于等容量策略和等数量策略，最优策略对应的缓冲区配置将数据通信时间分别缩短了40.5%和76.1%，将通信量分别减少了44.7%和77.8%.

5.3 变长规则存储机制

为了验证变长规则存储机制的优化效果，本文实验比较了应用变长规则存储机制前后的数据通信时间和通信量，如表5 所示. 由于统计上每条规则包含的规则函数数量约等于3，因此应用变长规则存储机制后，平均每条规则数据的大小为12 B，此时由于每条规则数据占用的局存空间变小，从核每次DMA可以加载更多的规则到局存中，从而大幅度减少了加载规则的DMA 次数. 同时由于规则集的总大小减小，从核的数据通信时间和通信量分别减少了89.0%和89.3%.

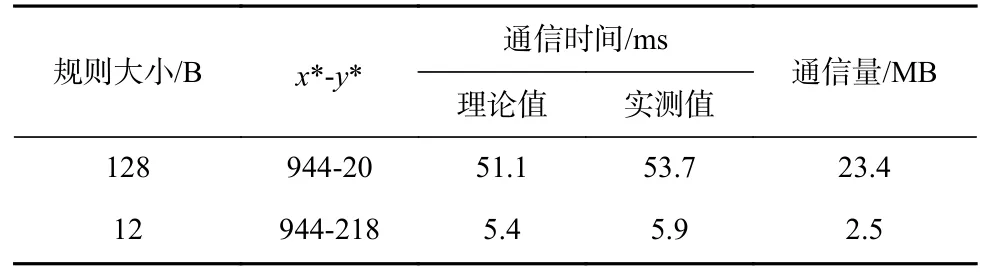
Table 5 Communication Time and Data Traffic Under Different Rule Sizes表5 不同规则数据大小下的通信时间与通信量

5.4 负载均衡机制

为了测试负载均衡机制的优化效果，本文实验构造了一个包含1 280 万条口令的字典，字典中的口令按照长度由短到长排序，最短的口令长度为1，最长的口令长度为28，然后比较了均匀数量方案与负载均衡方案下64 个从核的规则变换执行时间与执行时间的标准差，结果如图19 所示. 实验中使用了Hashcat中使用频率最高的规则集best64 作为测试规则集，规则函数的实现版本为CWISE，每个工作集包含的口令数量为256.从图19 中可以发现，在均匀数量方案下各个从核执行规则变换最短时间为3.10 s，最长为4.80 s，二者相差1.70 s，这意味着在这1.70 s 内，很多从核处于空闲状态，没有得到充分利用. 而在负载均衡方案下，每个从核的规则变换执行时间均为4.15 s，所有从核自始至终均处于忙碌状态，因此负载均衡方案下从核阵列的规则变换执行总时间比均匀数量方案少了13.5%.

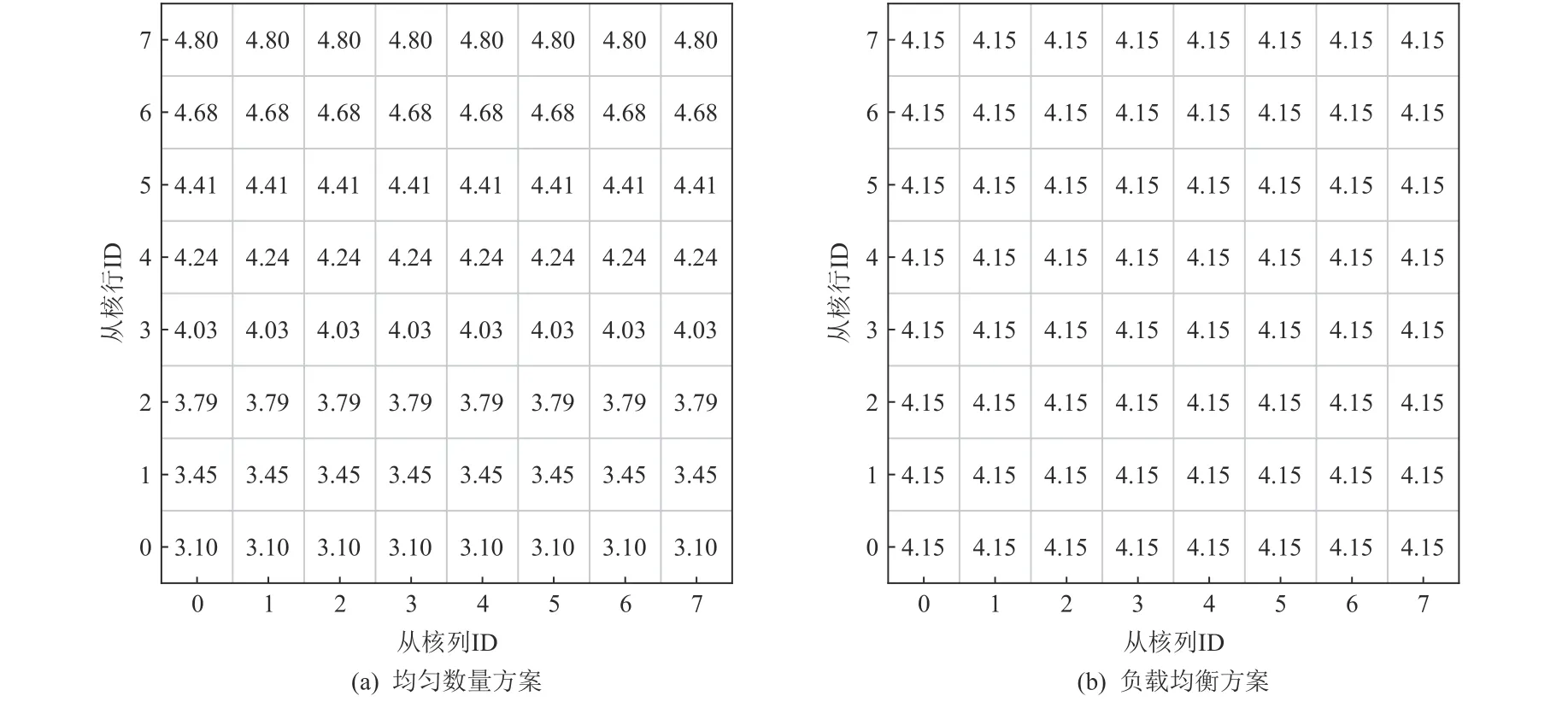
Fig.19 Rule mangling execution time of the slave cores under different policies图19 不同方案下从核的规则变换执行时间

为了验证工作集大小对负载均衡机制优化效果的影响，本文实验还测试了不同工作集大小下的从核阵列规则变换执行时间，结果如表6 所示. 观察表6 可以发现，负载均衡方案下各个从核执行时间的均值大于均匀数量方案，这是因为负载均衡方案需要访问主存中的信号量，因此产生了额外的开销.工作集太小时（例如64），从核阵列需要重新获取工作集的次数最多，并且不能充分利用局存中的P 缓冲，因此开销也越大. 随着工作集的大小增加，从核阵列重新获取工作集的次数减少，但这也导致不同从核间的规则变换执行时间极差变大. 综合考虑以上因素，将工作集大小设置为与P 缓冲同等大小较为合适.

Table 6 Rule Mangling Execution Time of the Slave Cores Under Different Workset Sizes表6 不同工作集大小下从核的规则变换执行时间

5.5 SIMD 优化效果对比

本文实验测试了CWISE，OPT32，SWV 这3 种规则函数实现版本中执行单次规则函数需要的平均时钟周期数. 为了充分展现并行优化的效果，实验中大部分规则函数使用长度为24 的口令进行测试，部分会使输出口令长度加倍的规则函数则使用长度为15的口令进行测试以避免输出口令超出最大口令长度.

图20 比较了OAC 类型规则函数的优化效果，8种规则函数中除了函数replace外其余函数均包含了大小写转换操作. 由图20 可以看出，OPT32 版本的时钟周期数约为CWISE 版本的1/3，SWV 版本的时钟周期数约为CWISE 版本的1/6、OPT32 版本的1/2，这说明提升单条指令同时处理的字符数能够有效减少OAC 类型规则函数消耗的时钟周期. 从图20 中还可以发现，CWISE 版本的函数toggle_case消耗的时钟周期数约为函数lowercase的2 倍，这是因为CWISE版本函数中既要判断一个字符是否为小写字母，也要判断其是否为大写字母，这导致执行时间加倍，OPT32 版本和SWV 版本因为采用了优化后的大小写判断机制没有发生此现象.OAC 类型规则函数中还包括3 种使用了字符匹配的规则函数title，title_w/separator，replace. 比较函数replace的性能可以发现，由于CWISE 版本和OPT32 版本均采用了逐个字符匹配替换方案，因此二者性能相同. 而SWV 版本使用了SIMD 并行字符匹配方案，不仅提升了字符匹配的速度，而且便利了匹配完成后的字符并行替换操作，因此提升了性能.

Fig.20 Optimization results of the OAC-type rule functions图20 OAC 类型规则函数的优化效果

图21 比较了OSC 类型规则函数的优化效果，由于此类规则函数实质上只对单个字符进行了操作，所以CWISE 版本和OPT32 版本执行时间非常短，而在申威SIMD 指令集中由于没有对向量中单个字节进行操作的指令，要实现对单个字节的修改，必须首先生成掩码，然后对所有字符执行同样修改，最后通过掩码将单个字符修改合并回原向量，这一过程使得SIMD 优化后的规则函数性能反而下降.

Fig.21 Optimization results of the OSC-type rule funtions图21 OSC 类型规则函数的优化效果

注意到SWV 版本的相邻2 次规则函数调用之间使用SIMD 向量传递口令，而CWISE 和OPT32 版本则使用局存传递口令，因此无法将SWV 版本函数与CWISE 或OPT32 版本函数混合使用，这会带来更大的口令数据转换开销，所以实际应用中若OSC 类型规则函数占比过多，反而会导致整体性能下降.

图22 比较了MSC 类型规则函数以及函数purge和函数nothing的优化效果，其中函数nothing实质上不做任何操作，因此函数nothing的执行周期数可以作为衡量函数调用开销的指标，即单次规则函数开销约为60 个时钟周期.MSC 类型规则函数包含了1或2 次字符移动，这种情况下SIMD 指令难以发挥其并行能力，并且需要多条指令组合才能实现移动，因此导致性能下降. 函数purge由于其特殊性，难以使用SIMD 指令实现相同功能，所以SWV 版本中先将向量寄存器中的口令存储于局存空间，然后使用普通标量指令对其进行操作，最后再将结果存回向量寄存器，这导致SWV 版本的函数purge实现包含了一次SIMD 向量存储开销和一次SIMD 向量加载开销，其性能变为CWISE 版本和OPT32 版本的3 倍. 由于函数purge在实际应用中占比约为0.2%，所以SWV版本的性能下降不会对整体性能产生明显影响.

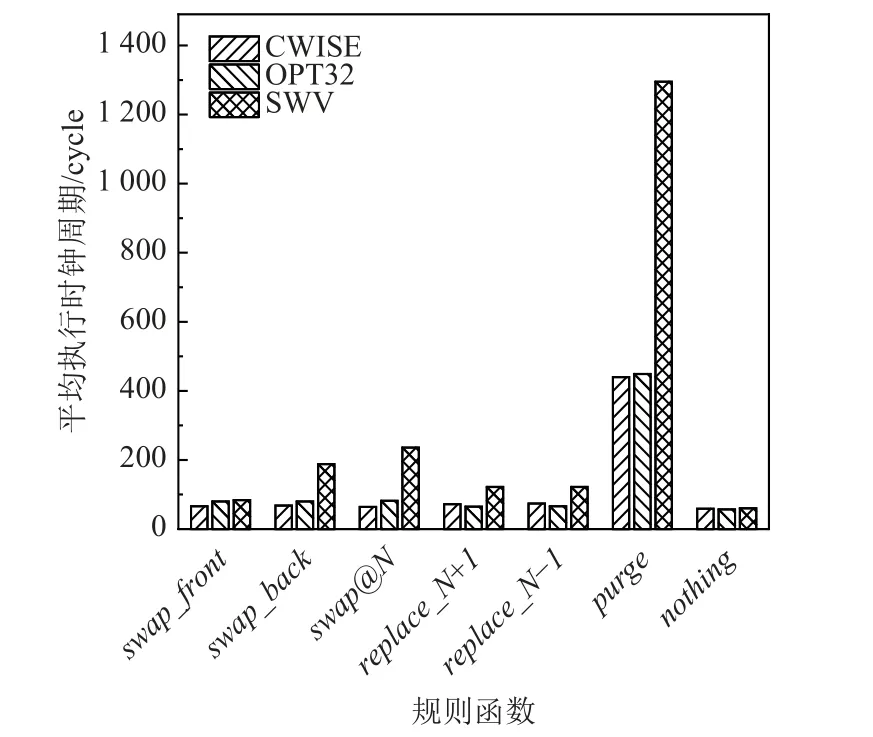
Fig.22 Optimization results of the MSC-type rule functions and purge, nothing rule funtions图22 MSC 类型规则函数以及规则函数purge，nothing 的优化效果

图23 比较了MAC 类型规则函数的优化效果，此类函数大多包含了字符移动操作，以truncate_left函数为例，要对长度为24 的口令应用truncate_left操作，需要将23 个字符各向左移动1 B，CWISE 版本和OPT32 版本中均不能一次完成，而SWV 版本则可以通过向量整体移位用1 条指令完成. 其他函数中也或多或少用到了向量整体移位指令，由于缺少相关指令，申威SIMD 指令集不擅长在口令末尾添加、修改字符的操作，因此在少量函数上SWV 版本的性能出现了下降，例如append_character，duplicate_last_N，truncate等，这一点类似于OSC 类型规则函数. 在函数reverse，reflect，duplicate_all中，SWV 版本使用了向量混洗指令，取得了1 倍以上的性能提升.

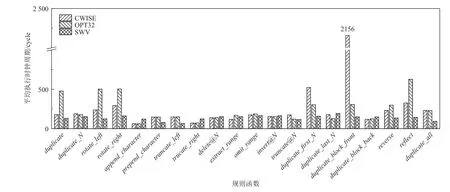
Fig.23 Optimization results of the MAC-type rule functions图23 MAC 类型规则函数的优化效果

5.6 整体优化效果

图24～26 展示了本文提出的优化方案的整体优化效果，实验测试了不同口令恢复系统实现方案下NTLM，MD5，SHA1 这3 种加密算法的口令恢复速度. 在系统架构方面，本文实验测试了纯主核口令生成方案（MASTER）和从核口令生成方案（SLAVE），其中MASTER 方案为主核负责口令生成、从核负责口令验证，SLAVE 方案为本文提出的方案，口令生成与口令验证均由从核负责. 在规则函数实现方面，本文实验测试了CWISE，OPT32，SWV 这3 种版本，其中CWISE 版本和OPT32 版本代码均来自于Hashcat，SWV 版本为本文提出的SIMD 优化版本. 组合上述方案一共可以得到6 种具体实现方案，但由于SW26010 主核不支持部分SIMD 指令，因此无法测试MASTER-SWV 方案的性能. 因为不同规则集包含的规则数量、规则函数的分布均有所差异，相应的口令恢复速度亦有所不同，本文实验选取了具有代表性的5 个常用规则集进行测试，它们分别为best64，rockyou-30000，unix-ninja-leetspeak，dive，d3ad0ne.

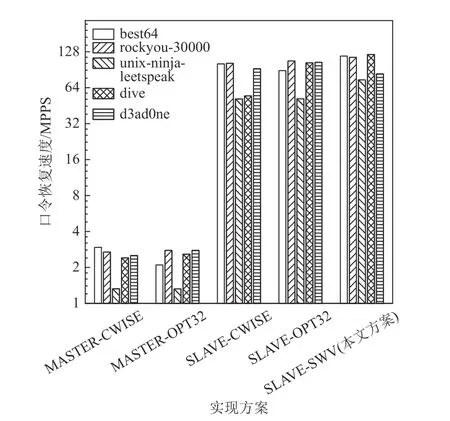
Fig.24 Password recovery speed of NTLM algorithm under different implementations图24 不同实现方案下NTLM 算法的口令恢复速度

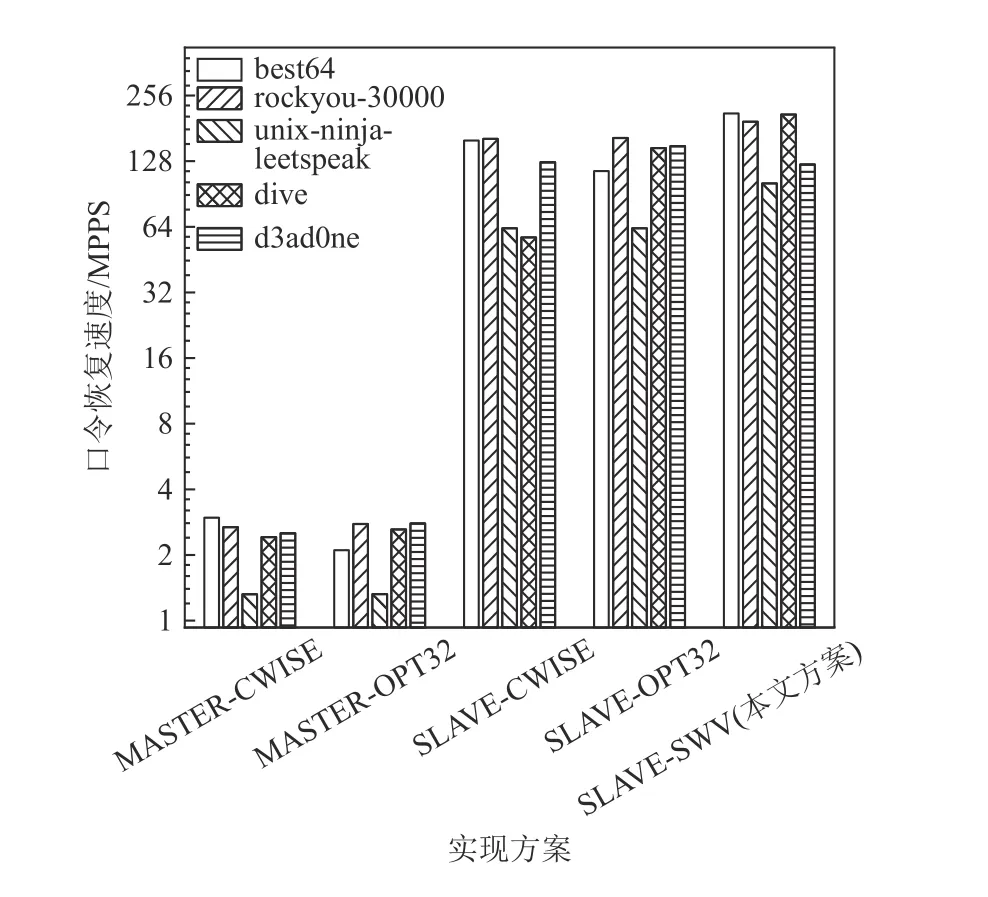
Fig.25 Password recovery speed of MD5 algorithm under different implementations图25 不同实现方案下MD5 算法的口令恢复速度

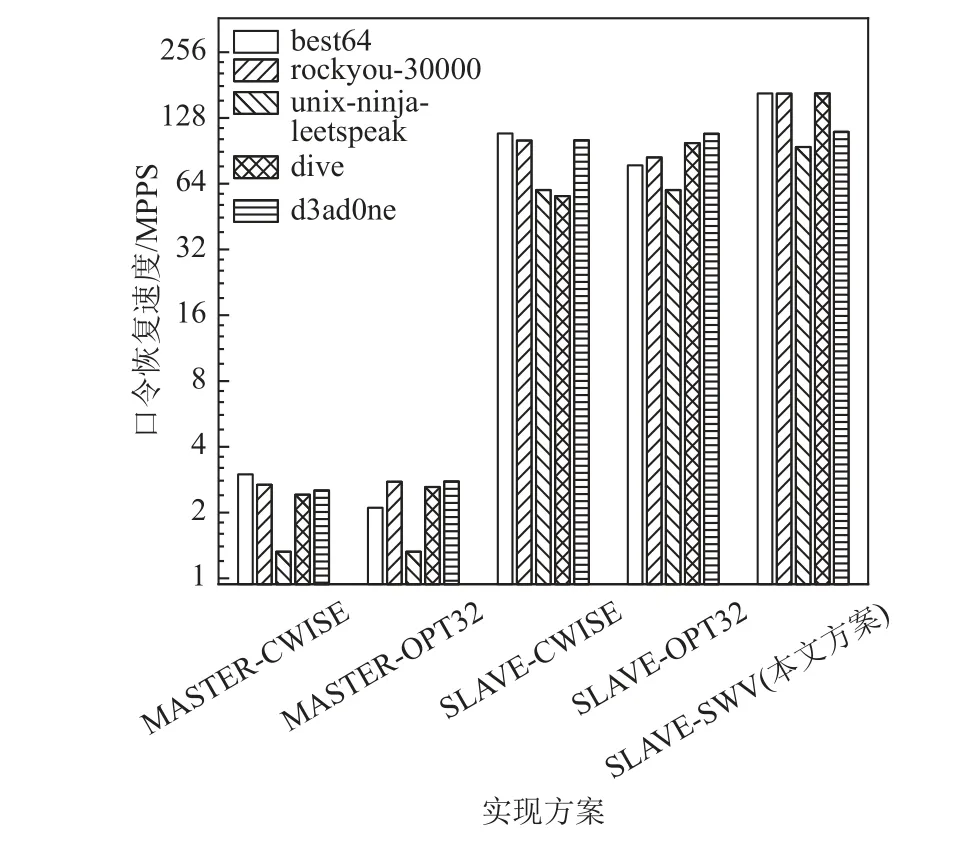
Fig.26 Password recovery speed of SHA1 algorithm under different implementations图26 不同实现方案下SHA1 算法的口令恢复速度

以NTLM 算法为例分析，对比MASTER-CWISE和SLAVE-CWISE 这2 种方案，可以发现前者的速度仅为后者的2.9% ～ 4.4%，显然这是因为主核的规则处理速度远小于从核的口令验证速度，因此成为了性能瓶颈，而将规则处理映射到从核后速度大幅度提升，进而使整体性能得到了提升. 对于NTLM，MD5，SHA1 这3 种算法而言，将规则处理映射到从核阵列带来的性能提升分别为34.1，41.7，36.5 倍.

对比SLAVE-CWISE，SLAVE-OPT32，SLAVE-SWV这3 种方案，可以发现三者在不同规则集上的速度表现有所差异. 在best64 规则集上，OPT32 版本的性能低于CWISE 版本和SWV 版本，这是因为best64 规则集包含大量的规则函数rotate_left，rotate_right，对此类规则函数，OPT32 版本的性能表现不佳. 在unixninja-leetspeak 规则集中，所有的规则函数均为函数replace，因此CWISE 版本，OPT32 版本的速度相同，而SWV 版本的速度提升了44.5%，这一结果与图20中单次函数replace的执行周期数相符. 总体来看，在best64， rockyou-30000， unix-ninja-leetspeek， dive 规则集上，SWV 版本的规则函数实现相较于CWISE 版本使系统速度提升了12.4% ～ 266.2%，相较于OPT32版本使系统速度提升了7.4% ～ 113.3%. 在d3ad0ne 规则集上，SWV 版本的性能劣于CWISE 版本和OPT32版本，原因在于该规则集包含了大量SWV 版本不占优势的规则函数swap@N，overwrite@N，purge等.

5.7 与其他工作对比

本文实验测试了应用本文优化方案后NTLM，MD5，SHA1 这3 种算法在完整的SW26010 处理器上的性能，并与业界主流的Hashcat 系统进行了对比.Hashcat 系统运行于台式工作站，CPU 型号为Intel Core i7-10 700，GPU 型号为AMD Radeon Pro WX3200.由于Hashcat 能够在纯CPU 模式和GPU 加速模式下运行，本文实验分别将这2 种模式命名为Hashcat-CPU 方案和Hashcat-GPU 方案. 测试结果如图27～29 所示.

Fig.27 Password recovery speed comparison of NTLM algorithm图27 NTLM 算法的口令恢复速度对比

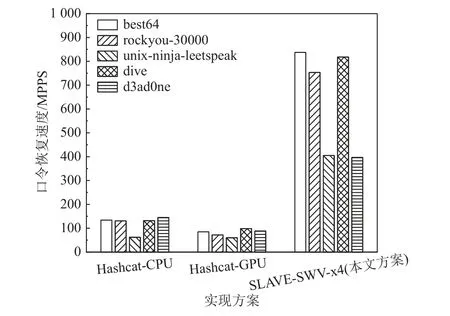
Fig.28 Password recovery speed comparison of MD5 algorithm图28 MD5 算法的口令恢复速度对比

Fig.29 Password recovery speed comparison of SHA1 algorithm图29 SHA1 算法的口令恢复速度对比

测试结果表明，经过本文方案优化后的SW26010单节点口令恢复系统性能大幅度超越运行于Intel 和AMD 处理器上的Hashcat 系统，在NTLM，MD5，SHA1这3 种算法上分别提升了1.94，2.74，3.04 倍以上，充分体现了国产申威众核处理器在口令恢复领域相较于国外处理器的性能优势.

6 结 论

本文的研究目标是申威众核处理器平台上口令恢复系统的性能优化问题. 针对规则模式下口令生成速度性能瓶颈，本文首先从线程级和数据级2 个维度分析了规则处理算法的可并行度，然后结合SW26010 处理器的硬件架构，提出了切实可行的优化方法，其中主从核任务映射和从核任务分配机制解决了规则处理算法的并行分解问题，使其能够通过从核阵列进行加速；从核缓冲区配比优化机制解决了如何将LDM 空间高效分配给口令数据和规则数据的问题，降低了从核阵列的数据通信时间和通信量；变长规则存储机制消除了规则数据的存储冗余，减少了数据通信量；负载均衡机制提高了从核的利用率，降低了整体执行时间；最后，基于申威SIMD指令集实现的规则函数向量优化减少了规则函数执行消耗的时钟周期，进一步提升了规则处理的速度.

本文基于神威·太湖之光超算节点进行了实验评估，测试了应用本文优化方案前后的NTLM，MD5，SHA1 这3 种算法的规则模式口令恢复速度. 实验结果表明，本文提出的优化方案将原有系统的规则模式口令恢复速度提升了30 ～ 101 倍，从而解决了原有系统中基于规则的口令生成速度瓶颈问题，增强了申威处理器平台上口令恢复应用的实用性.

同时，本文实验也表明，申威处理器在执行规则处理任务时仍存在一些不足，首先SW26010 处理器的SIMD 指令集不支持以8b（1B）为基本操作单元的指令，导致指定字符变换（OSC）和指定字符移动（MSC）类型规则函数的SIMD 实现效果不佳，性能甚至低于原有实现；其次，口令数据与SIMD 向量的互相转化开销较大，这也导致了函数purge的SIMD 向量化实现速度较慢；最后，SW26010 处理器本质上仍是冯·诺依曼架构的通用处理器，由于通用处理器依赖指令操作数据且数据必须经由存储器在不同指令间传递，在口令恢复这种数据密集型应用中会产生大量的存储器读写开销，增加了能耗. 目前看来，突破冯·诺依曼架构探索更加专用的领域架构，是未来提升口令恢复系统的性能和能效的解决方案.

作者贡献声明：张振东提出了研究思路和实验方案，并完成主要实验和论文撰写；王彤负责了部分实验；刘鹏提出研究思路并修改论文.