从唯一性定理到场计算
2024-01-12汤一铭
张 明 汤一铭 包 扬
(南京邮电大学 电子与光学工程学院、柔性电子(未来技术)学院,南京 210023)
电磁场的唯一性定理是所有电磁场计算的出发点,是大学和研究生阶段“电动力学”和“电磁场理论”等课程的主要内容之一。电磁场计算是学习“电磁场理论”等课程的最终目的,课程中会学到分离变量法、格林函数法、Stratton-Chu公式,甚至一些数值方法。但学生在课程学完后,往往只停留在了解很多孤立的“知识点”,对各“知识点”之间的关联并没有深入地讨论和思考。本文分别从静电场和时谐场唯一性定理及相应电磁场计算所需条件出发,讨论电磁场唯一性定理与电磁场计算之间的关联,并用三个边值问题具体说明此关联。
1 电磁场唯一性定理
1.1 静电场唯一性定理
设一封闭区域V,其边界为S+S∞,如图1所示。如果这区域中的电荷分布ρ(r)确定,并且下列三项任意一项确定,则V区域内静电场的电位φ(r)是唯一的(当然电场强度E也为唯一,因为E=-Δφ。另外,电荷分布在有界区域,设φ(S∞)=0)[1]:

图1 V区域内静电场的电位
(1)S面上电位φ∣S;

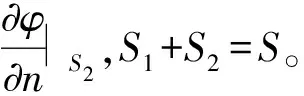
1.2 时谐电磁场唯一性定理
对于时谐场,封闭区域V,边界为S+S∞,如图2所示。

图2 V区域内时谐电磁场
(1)区域V边界上电场强度E的切向分量Et确定;
(2)区域V边界上磁场强度H的切向分量Ht确定;
(3)区域V部分边界上电场强度E的切向分量Et确定,剩余边界上磁场强度H的切向分量Ht确定;
只要满足上述三条件中任何一个,则区域内由电流源J和磁流源M产生的电场E和磁场H是唯一的。(在S∞面,电磁场满足辐射条件[2])
2 电磁场计算
2.1 静电场电位计算
我们自然关心满足场唯一性定理的条件后,如何计算静电位。为回答这个问题,让我们利用电位满足的泊松方程,
(1)
如图1所示,式(1)中ρ(r)是r处的电荷密度,ε为r处的介电常数。并利用格林恒等式和格林函数,可以写出V内电位的计算式[2]
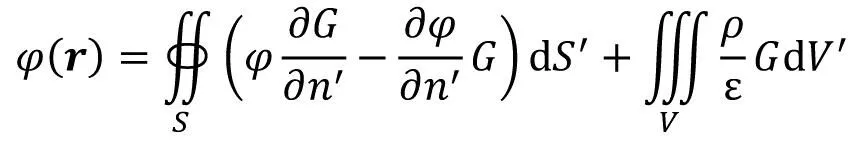
(2)

2.2 时谐电磁场场计算
计算时谐辐射场有著名的Stratton-Chu公式[3]
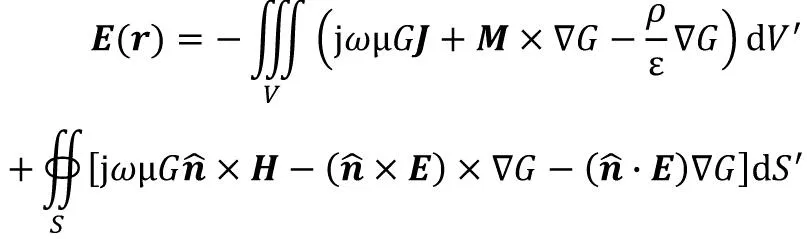
(3)
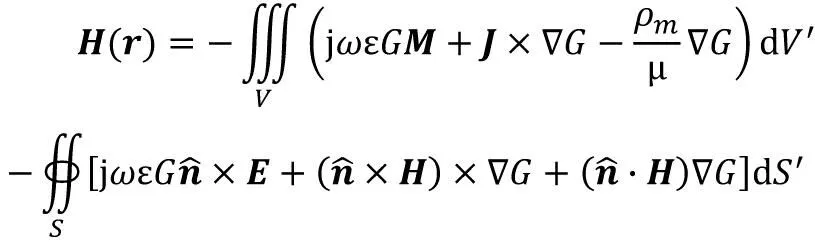
(4)

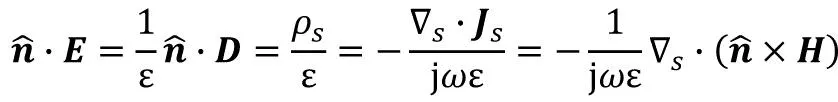
(5)
上式推导过程中用到电位移矢量D的边界条件以及面电流密度Js和面电荷密度ρs的关系式,▽s表示曲面上二维拉普拉斯算子。同理可得

(6)

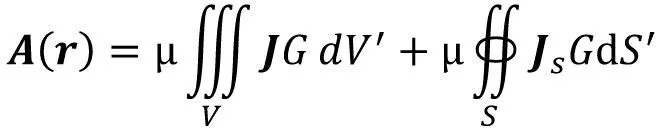
(7)
在洛伦兹规范下,由A(r)可计算相应电场EA(r)和磁场HA(r),
(8)
(9)
同样,磁流源与全空域格林函数的积分得矢量电位F(r),由F(r)可计算相应电场EF(r)和磁场HF(r),
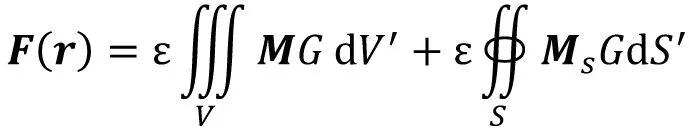
(10)
(11)
(12)
电/磁流源的总电磁场为
E(r)=EA(r)+EF(r)
(13)
H(r)=HA(r)+HF(r)
(14)
可以证明(13)(14)分别和(3)(4)完全一样。
3 唯一性定理与场计算的讨论
由上述讨论可见,计算时谐辐射场不仅需要已知边界电场强度的切向分量,同时还需要已知边界磁场强度的切向分量,此要求高于时谐电磁场唯一性定理的条件。计算静电场情况也有类似情况。
实际上,从数学角度看,求解静电场的电位,是解满足泊松方程(偏微分方程)及一定边界条件的边值问题。同样,求解时谐电磁场,是解满足亥姆霍兹方程(偏微分方程)及一定边界条件的边值问题。唯一性定理回答了这些边值问题在何种条件下,解是唯一的。由式(2)和式(3)~(14)可知,计算静电位或时谐电磁场需要已知两个边界条件(静电场:边界上电位及其法向导数;时谐场:边界上电场强度和磁场强度的切向分量),如果只已知其一,我们并不一定能用显式列出由已知的边界条件计算另一个边界条件的关系式。由此,我们不能在满足唯一性定理条件下直接用式(2)计算静电位或用Stratton-Chu公式(3)和(4)计算时谐电磁场。
4 电磁场边值问题求解方法
计算静电场的电位及时谐电磁场,需要求解相应的边值问题。常用的边值问题求解方法有解析方法和数值方法两大类。
4.1 解析方法
解析方法主要有分离变量法、镜像法和保角变换法等,它们的好处是场解可用解析公式直接表示,精度高,但仅适用于某些特定场景。典型场景如:边界与正交坐标系重合或可通过解析函数把边界变换成与正交坐标系重合,以及存在无限大导电/磁平面等情况。
4.2 数值方法
数值方法主要有有限差分法,有限元法和边界积分法等,数值方法的好处是可以处理任意形状和媒质的边值问题,通用性强,但数值方法做了某些近似,计算精度与网格划分、采用的近似技术、线性代数方程组求解器等许多因素有关。并且因为需要求解线性代数方程组,与解析方法相比需要更多计算机内存和计算时间。
边值问题求解方法还有高频近似方法,它适用于物理尺寸比电磁波波长大许多倍的应用场景。
4.3 例子
最后以三个电磁场边值问题为例考察唯一性定理与场计算之间的关联。
1)带电导体的电荷分布
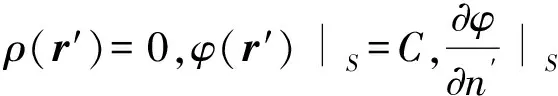
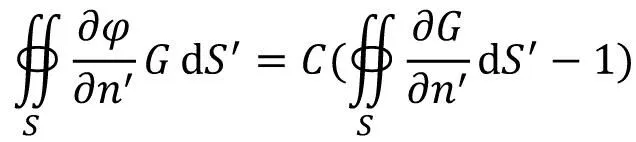
(15)
2)理想电导体的电磁散射

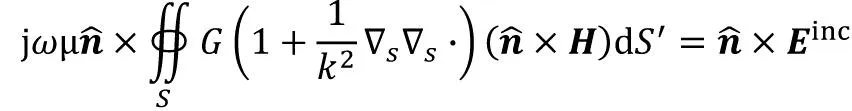
(16)

从上面两个边值问题可见,在已知一个边界条件:导体表面的电位/理想导体表面电场强度切向分量为零,边值问题有唯一解。然后我们需要求解边值问题得到另一边界条件:导体表面电位的法向导数/理想导体表面磁场强度切向分量,最后由两个边界条件一起计算区域内的电位/电磁场。
3)介质圆柱体的电磁散射
圆柱的边界是半径为a的圆柱面,在圆柱坐标系可简单表示为ρ=a,所以可用解析方法之一的分离变量法求解。以TMz极化均匀平面入射波为例,入射波电场在z方向,可用柱面波展开为
(17)
式中E0为入射波幅度,Jn(*)是n阶贝塞尔函数,k为柱外媒质中的波数。由麦克斯韦方程组可以计算得入射磁场Hinc。圆柱体外还有散射场,散射场也可由柱面波表示为

(18)
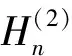
在介质柱内总场满足亥姆霍兹方程,也可展开为柱面波
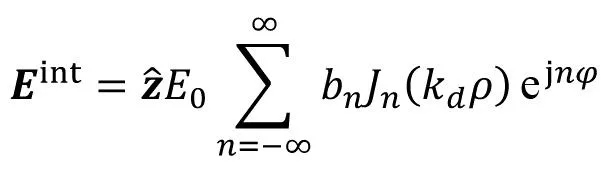
(19)
式中bn为待定展开系数,kd为介质柱中的波数,展开式中没有选纽曼函数是因为柱内区域含圆柱中心,而纽曼函数在柱体中心处发散。同理,由麦克斯韦方程组计算得柱内磁场Hint。
最后由电磁场在圆柱体表面的切向分量连续
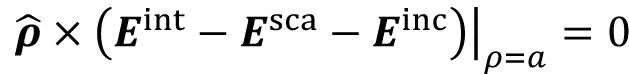
(20)
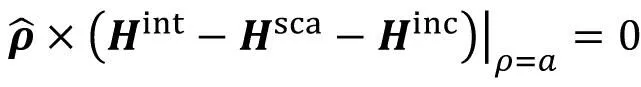
(21)
联列(20)和(21)求解得展开系数an和bn[6]

(22)
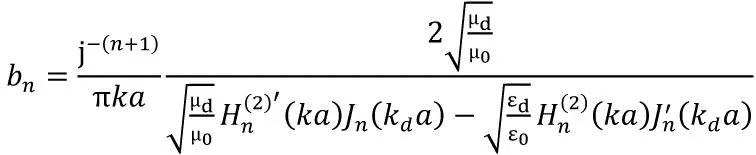
(23)

在这个问题中,貌似既不知边界上的切向电场,也不知边界上的切向磁场,与唯一性定理的条件不符。实际上,介质柱的电磁散射含两个边值问题,即柱外的散射场和柱内的总场。由边界条件可知,这两个边值问题的边界上切向电场的差为入射电场的切向分量,而边界上切向磁场的差为入射磁场的切向分量。由此,我们需要联立式(20)和(21)才能解出场计算需要的边界切向电场和切向磁场。
同样的例子如匀强电场中的介质球,我们并不直接知道介质球表面的电位或其法向导数,但可以通过电位和其法向导数的边界条件联列解出边界上的电位或其法向导数。从而能计算由介质球引起的电位变化。
5 结语
课程学习中,各部分内容之间的逻辑关联对学生完整和深入掌握课程知识非常重要,但在教学过程这一环节往往被忽视。本文给出了电磁场唯一性定理的条件与场计算所需条件的差异,讨论了两者的关联。以边值问题为例说明了在满足场唯一性定理后,如何求解电磁场边值问题,并最终计算区域内电磁场的过程。由此强化了课程知识点间的内在关联。
