有载二端口网络几何分析法及其应用

陈希有 齐 琛 李冠林 牟宪民 陈建辉

(大连理工大学 电气工程学院,大连 116023)

在电气、电子工程中,很多问题可以抽象成二端口网络模型加以研究,例如滤波器、阻抗变换电路、PID调节电路、非接触电能传输系统、选频网络,等等。因此,二端口网络的任何分析方法,都具有广泛的应用对象。解析分析法和数值分析法,是目前普遍采用的两种方法。二者共同弊端是,当某参量发生改变时,难以直观地看出二端口网络的主要电气量是如何联动变化的,这给预测变化趋势和优化设计带来不便。解析几何是一种借助于解析式进行图形研究的几何学分支。它采用数值的方法来定义几何形状,并从中提取数值的信息。人类对事物的认知特点是,习惯接受用图形表达的信息,而费解于用复杂公式和数据串表达的信息。据此,本文参照文献[1],结合我国习惯,向读者引介一种用复平面解析几何原理,分析有载二端口网络的方法。文中以等效负载阻抗模即|ZL|为自变量,通过一张平面图形,便可获得包括输入电流、输出电流与电压、输入功率、输出功率,以及传输效率在内的当前信息和变化趋势。该原理扩展了二端口网络的分析方法,并能促进复变函数和解析几何在电路分析中的应用。

1 输入电流及其映射轨迹

有载二端口网络如图1所示,其中负载复阻抗ZL=|ZL|ejφL。根据教科书,二端口网络传输参数方程用T矩阵表示为[2]

图1 有载二端口网络

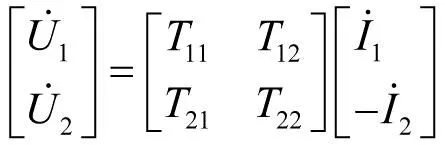
(1)

图1的输入阻抗为

(2)

(3)

(4)

为了获得上述系数的物理意义,再依次计算以下各量。

令式(4)中|ZL|→∞,得到输出端口开路时,输入端口电流为

(5)

再令式(4)中|ZL|=0,得到输出端口短路时,输入端口电流为

(6)

上述电流之差为

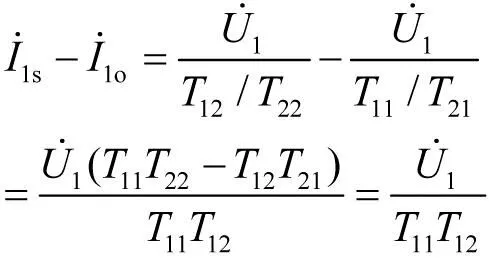
(7)

在输入电压和网络参数一定的条件下,上述电流在复平面上有固定的长度和方向。

根据方程(1),输入端口处于短路状态时,从输出端口看进去的等效阻抗为

(8)

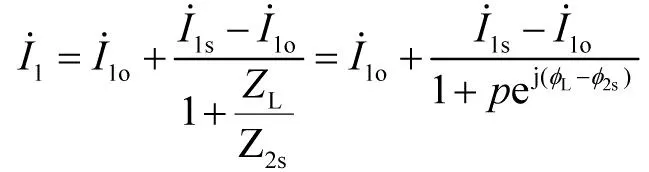
(9)

式中,

(10)

图2 电流的映射轨迹及I2和U2的几何读取

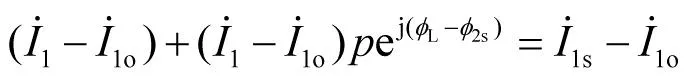
(11)

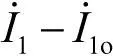
利用弦长和圆周角可以求出这个圆弧的半径,结果是

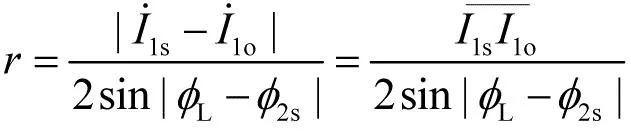
(12)

2 I2与U2的几何读取

由传输参数方程求得输出电流为

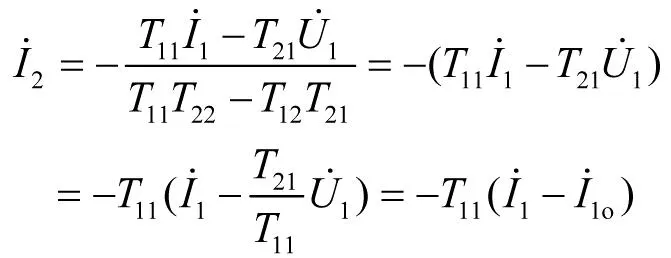
(13)

(14)

可见,I2的大小正比如图2中的线段l1。

由于U2=|ZL|I2,所以,为了能够从线段长度上得到U2的大小,需要寻找ZL与已知相量的关系。为此,由式(9)得

(15)

(16)

3 阻抗|ZL|和输入功率P1的几何读取

如果已知I1,可以通过图中线段的长度,确定所需要的|ZL|,数学上相当于求逆映射。根据式(12)和(16),将|ZL|写成

(17)

图3 |ZL|和P1的几何图

(18)

再根据式(17)、(18),|ZL|可以用线段长度表达如下:

(19)

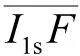
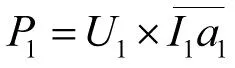
(20)

4 输出功率P2和传输效率η的几何读取

根据式(14)和式(16),输出平均功率可以写成

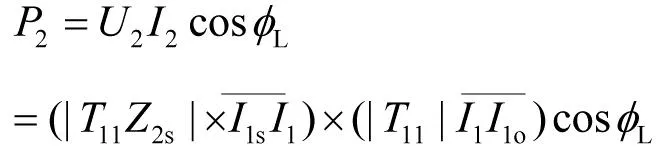
(21)

由于图4中ΔI1oI1I1s和ΔI1oa2I1有一个公共角即∠I1sI1oI1,并且∠I1oI1I1s与∠I1oa2I1相等(都等于弦切角∠I1sI1oI1),所以ΔI1oI1I1s∽ΔI1oa2I1,故

图4 P2和η的几何读取

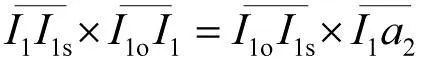
(22)

将式(8)、式(22)代入式(21)得,

(23)

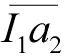
根据输出和输入功率的读取公式,即式(23)和式(20),得效率表达式为

(24)

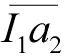
(25)

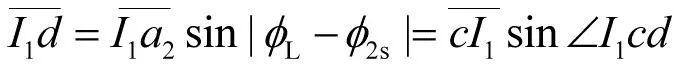
(26)

将式(25)、式(26)代入式(24)得

(27)

(28)

图4中存在相似直角三角形,即Δefh∽Δekc,因此

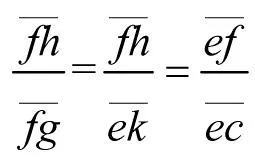
(29)

将式(29)代入式(28),结果再代入式(27)得

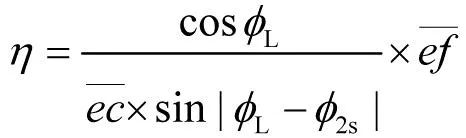
(30)

5 在非接触电能传输系统分析中的应用

非接触电能传输(Contactless Power Transmission,CPT),是指不通过导线或导体连接,利用某种场或波,在一定距离内实现电能的有效传输。

图5 感应耦合CPT系统简化电路模型

从电路模型上看,CPT系统可以抽象成有载二端口网络,如图5所示。利用电路理论,可以很容易求出二端口网络的某种参数方程。这样,对CPT系统电气性能的分析,就变成了对该有载二端口网络的分析。

基于本文第2至4节的解析几何分析原理,本文设计了“非接触式电能传输系统的几何分析法”软件[4]。可以选择四种阻抗补偿结构,针对每种结构,都能用几何图形描绘出等效负载阻抗及其他元件参数变化时,主要电气量的联动变化趋势。软件设计了许多交互内容,可以通过交互窗口设置元件参数,几何分析法软件交互操作主窗口如图6所示。

图6 几何分析法软件交互操作主窗口

当ZL设置为电阻(在CPT系统中总是希望得到电阻性负载),从初始的10 Ω,按照30 Ω的步进量变到250 Ω,可以得到如图7所示的图像。由图7可见,随着负载阻抗模的增大,输入电流沿着圆弧逐渐上移,输入电流值逐渐减小,输出电流也逐渐减小,输出电压则逐渐增大;输入有功功率先增大到一个最大值后,又很快下降;输入无功功率逐渐减小,开始减小得很快,之后较慢;输入侧功率因数角先减小后增大。

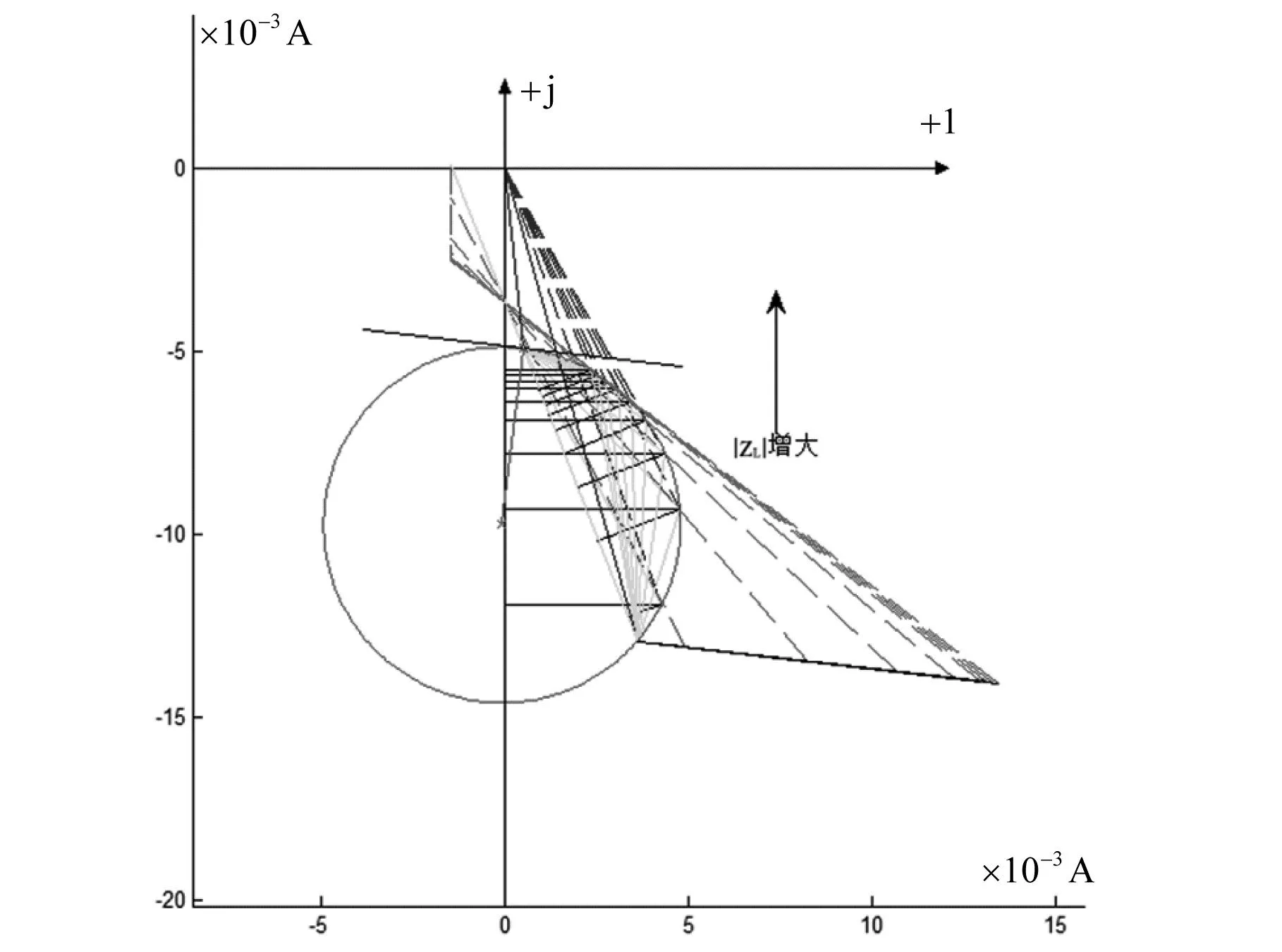
图7 |ZL|步进变化时CPT系统电气量的联动变化

图8 φL步进变化时CPT系统电气量的联动变化

6 结语

在电路分析中,除了使用各种解析法和数值法外,还可以有条件地使用包括解析几何在内的各种图解法,这是因为按正弦规律变化的电压和电流,可以变换为复数的电压相量和电流相量,这些相量都对应着复平面的有向线段。当电路某参量发生变化时,这些相量就会随之变化,即数学意义上的映射。根据映射的几何图形进行分析,可以很直观地看出各电气量之间牵一发而动全身的联动关系。这样可以促进教学内容的创新,并促进复变函数在电路分析中的应用。