基于树莓派和Python的数字均衡器实验设计
2024-01-12彭里卓张建良
孙 晖 彭里卓 张建良
(浙江大学 电工电子国家级实验教学示范中心,杭州 310027)
“信号分析与处理”是电气工程类专业本科生必修的一门技术基础课程,传统的配套实验以个人电脑软件仿真为主,与工程应用联系不紧密,难以激发学生的学习热情[1-2]。因此浙江大学广泛开展了基于综合硬件平台的实验,加强对学生专业应用能力、工程推理能力和解决问题能力的培养以及团队协作能力、创造性能力的培养[1]。
传统的实时性数字音效处理系统主要通过以DSP为核心的硬件进行软硬件结合开发[3-5]。但本科生直接利用DSP芯片进行开发的难度和成本都较高。为了促进学生综合利用课程相关知识解决实际问题,考虑到Python的易用性和树莓派平台的高性价比,本文基于尖峰滤波器均衡器模型[6-7],提出基于树莓派和Python的数字均衡器实验设计。
1 树莓派和Python
树莓派是一款高性价比的微型电脑,其处理器基于ARM架构,系统基于Linux。作为树莓派主要编程语言的Python是一种功能强大的免费开源计算机高级编程语言,具有极强的跨平台性、可拓展性以及胶水特性,容易学习,可读性强,是初学编程者最佳的学习对象之一。
2 实验原理
均衡是一种常见的音频处理手段,目的是放大或减弱音频信号的某些频率范围,从而改变音频信号的音色。
均衡器可分为图形均衡器和参数均衡器。数字图形均衡器结构[8]如图1所示,这种均衡器将整个音频段分为若干频带,每个频带放置一个带通滤波器,滤波器中心频率和带宽固定,而增益和总增益可以调节。

图1 N段图形均衡器网络结构
图1中,HN(z)为第N个频段的滤波器系统函数,gN是第N个频段的增益,G为总增益,系统函数可写为:
(1)
用户通过自己手动调节各频段增益gi,即可对均衡器参数进行调节,从而获得不同效果的均衡器模型。
3 实验过程
在本实验中,HN(z)参考了TI公司公开的尖峰滤波器模型[7]:
已知二阶模拟带通滤波器系统函数
(2)
满足:
其中ω0是中心频率,k是中心频率处增益,α与品质因数/通带宽有关。
定义上下限频率ω+、ω-处,满足增益
因此在分贝单位上,上下限频率处的增益是中心频率的增益的一半。代入H(s)可计算得:
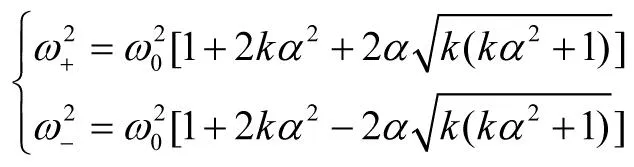
(3)
常见的图形均衡器将20 Hz至20 kHz的音频信号分为10段来调节,频率点以倍频程间隔分布[9],据此定义通带宽bw:
ω+=ω-·2bw
推得
(4)
联立式(3)(4)得到α关于通带宽bw的表达式:
(5)
得到由ω0、k和bw定义的模拟二阶带通滤波器:
(6)
其次用双线性变换法得到数字滤波器表达式,将H(s)映射到H(z)。
进行预处理,将模拟量转换为数字量:
(7)
(8)
将式(7)(8)代入式(6)得到:
(9)

最后为了方便调参,滤波器输入参数取为采样频率fs、中心频率f0、中心频率增益g和品质因数Q。
不妨令Q满足
(10)
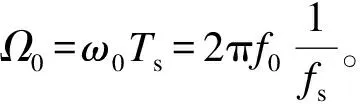

(11)
得到便于从输入参数计算的中间变量:

(12)
由式(9)(11)(12)得到最终滤波器参数:

(13)
综合得最终滤波器系统函数的表达式:
(14)
其中各参数由输入参数采样频率fs、中心频率f0、中心频率增益g和品质因数Q所决定,关系如式(12)、式(13)所示。
对于音频信号这类相位敏感信号,FIR滤波器的输出效果比IIR滤波器更稳定[10]。树莓派的运算能力较弱,而FIR滤波器使用快速傅里叶变换能够提高速度。于是,求得尖峰滤波器的IIR形式后,为使之能够在树莓派数字音效处理系统上使用,通过窗函数截取的方式将其转换为FIR滤波器形式。具体步骤为:设置好采样频率fs、中心频率f0、中心频率增益g和品质因数Q后,利用scipy库signal.dimpulse()函数[11]即可生成特定参数尖峰滤波器的单位脉冲响应,再用窗函数截取单位脉冲响应前部分即可得到对应参数的FIR滤波器的h(n)。截取点数越多,FIR滤波器就越逼近IIR滤波器[10],在不超出树莓派性能限制的原则上,点数可以尽量多。经过测试,当采样频率为44.1 kHz时,200以上截取点数就已经足够还原IIR滤波器。
对于本实验而言,采样频率fs统一设置为44.1 kHz,品质因数Q建议在[0,1]范围内取值,中心频率f0取值包括31 Hz、62 Hz、125 Hz、250 Hz、500 Hz、1kHz、2kHz、4 kHz、8 kHz和16 kHz共10种,中心频率增益g取值从-12 dB递增至12 dB共25种,因此本实验一个完整的均衡器由250种不同中心频率、不同增益的FIR滤波器构成。
至此完成了均衡器模型中最关键的带通滤波器设计,剩余工作是将输入音频信号分别与各频段带通滤波器FIR模型先卷积再求和,即可得到均衡器处理后的音频输出。使用scipy库signal.fftconvolve()实现卷积[12]。
4 实验结果
实验采用树莓派4B作为实验平台,采用外接屏幕、键盘和鼠标作为交互方式,使用Thonny IDE作为编程环境,使用Python3.7版本作为编程语言,实验平台如图2所示。
在树莓派上利用Python对各中心频率、各增益的均衡器模型输入单位脉冲,观察输出信号的幅度频谱,可以清晰地看出各频段的滤波效果,如图3、图4所示。
测试得品质因数设置为0.4时,相邻频段的相互影响处于比较合适的程度。当各滤波器的截取点数N为200左右时,树莓派处理速度较快。实验发现在低频处因为点数较少,而出现幅度偏差,因此需要针对低频增加FIR滤波器h(n)的点数。
将均衡器模型输入到文献[13]所构建的数字音效处理系统中,经过人耳试听,基本达到预期。调节不同的中心频率增益,可实现各种均衡器风格。
5 结语
(1)基于尖峰滤波器,提出了一种基于树莓派和Python的数字音效处理综合实验设计方案的实例,设计了在树莓派中实现数字音效处理系统可使用的FIR滤波器的具体过程,成功实现了均衡器效果。
(2)实践证明,设计的均衡器具有趣味性和拓展性,不仅加深了学生对理论知识的理解,锻炼了学生理论联系工程实际的能力,还使得学生有较高成就感,激发学生的创新思维。
