海上超长管道浮运受力和变形特性
2024-01-12刘泽瀚王元清李彬鹂
刘泽瀚,俞 缙,王元清,李彬鹂,王 磊
(1.厦门工学院 建筑科学与土木工程学院,福建 厦门 361021; 2.华侨大学 福建省隧道与城市地下空间工程技术研究中心,福建 厦门 361021; 3.厦门市政水务集团有限公司,福建 厦门 361008)
随着沿海城市的发展,对燃气、石油、自来水等自然资源的需求与日俱增,这些重要的自然资源常通过跨海管道的方式进行运输。常用的海底管道铺设方法主要包括顶管法、S 形铺管法、J 形铺管法、卷筒式铺管法、拖管船法和沉管法等[1-5]。其中,沉管法因其管道加工简单、所需设备常规、铺设效率高、水底地形适应能力强、对水上通航影响小等优点已成为跨海管道的主要铺设手段[6]。管道浮运是管道铺设过程的关键,相较于底拖法、离底拖法,浮拖法有以下优点[7-10]:浮运不受水深和海底地形影响;对拖船的拖力要求相对较低;在浮运过程中管道的变形和破损易于观测;浮筒和浮箱易于绑扎和解开回收,可降低工程造价。
管道在浮运过程的受力与变形依旧是目前研究的难点与重点。Wang 等[11]研究了水下倾斜不同长度同心圆管的动力特性,并根据小变形假设建立数学模型以确定管道相关参数; 李金成等[12-13]对管道在3 种不同拖曳方法下的受力进行研究,并依此建立管道拖航受力模型,开发了管道强度计算程序;Feng 等[14]提出了基于分布式光纤传感器的海底管道横向屈曲检测方法,认为屈曲检测的结果可用于评估管道的极限状态、检查屈曲形成的可靠性、确定屈曲中的峰值载荷和循环应力,以及验证管道设计;Ye 等[5]为了研究超长管道在沉放阶段的吊索张力、应变和位移的变化规律,进行了5 种物理模型试验,得到调整吊点位置可以减少管道位移但不影响吊索张力的结论;于孝民等[15-16]介绍了实际工程中沉管工艺,为后续工程提供了一定的借鉴意义。随着计算机技术的发展,数值模拟在沉管过程管道的受力变形分析中起到了关键作用。Teng 等[17]利用黏性流体模型对淹没水平圆柱体上的波浪作用进行了数值模拟,得出波浪频率和振幅会对圆柱体上所受波浪力产生显著影响的结论;Hu 等[18]用数值模拟方法研究波浪对非淹没水平圆柱的作用,水平圆柱在竖直方向受到的波浪力计算结果和Dixon 等[19]的波浪力计算结果相近;Guo 等[20]结合实际工程,分析管道漂浮时的应力状态,计算结果表明管道移动时应密切注意管道变形趋势,防止管道变形失控;Fang 等[21]对悬浮结构在不同荷载下不同锚索布置形式的受力进行分析,优化了锚索布置形式与适用范围;朱俊辉[22]则使用有限元法对浮运施工中管道的提吊变形进行了分析与优化。
目前的研究大多围绕沉管的施工方法步骤,以及管道受水流力或波浪力的力学响应。在海上管道浮运实际施工中,管道长度较长,管身变形控制难度较大,管道与流体相互作用,但以往研究中较少考虑管道长细比、管身弯折角度等因素的影响。为此,本文开展海上长管道浮运的流固耦合数值模拟,重点讨论水流、波浪作用下管道长细比、拖船数量、相对流速Vm、管身弯折角β对管道浮运时应变与位移的影响,以及波流联合作用下波浪周期T和波高H的影响。最后,依托厦门同安湾海域管道浮运施工项目,计算管道浮运水流阻力和波浪阻力,并分析浮运时管道的变形。
1 管道浮运变形数值模型
利用流体力学软件STAR CCM+以有限体积法(FVM)对流体域进行求解,固体力学软件ABAQUS 以有限元法(FEM)对固体域进行求解,两种软件的计算结果通过“inp”文件来实现流体-结构交界面的数据交互,属于分离式流固耦合FSI(fluid-structure interaction)。耦合计算时,通过在STAR CCM+中建立数值水槽的方法计算波流对水槽中结构物产生的压力和剪力,然后通过耦合面将计算出的压力和剪力传递给ABAQUS 中的管道模型,对耦合面进行基于流体计算结果的结构响应分析。
管道在海上浮运的设计及管道约束装置如图1(a)所示,参考相关文献[13,23],最终管道的受力简化如图1(b)所示,其中x为管道轴线方向,y为水流方向,z为重力方向。简化后的拖船约束及管道自重利用ABAQUS 进行计算,水流、波浪及浮力则利用STAR CCM+控制。

图1 管道浮运受力模型Fig.1 Force model of pipeline floating transport
流域尺寸由模拟波浪时确定,波浪入口到出口之间距离总长为10 个波长并在出口前设置2 个波长的消波区以阻止波浪的反射[24]。流域网格在管道附近采用切割体网格,其余位置采用六面体网格并在管道周围和自由水面附近的网格进行加密[25-26]。流体入口由流速控制,出口则由压力控制,底部设置为壁面,管道周围设置边界层以确保准确捕捉水流力与波浪力,其他边界设置为对称面。管道采用实体单元的形式建模,为贴合实际工程,材料选用Q345 钢材物理属性,管道投影长500 m,管道壁厚20 mm。
为初步研究不同管道长细比、拖船数量、管道弯折角度、波流联合作用对管道应变与变形的影响,根据厦门气象站 20 年风向、风速统计资料,以及工程区附近水文观测站流速数据,本次模拟工况见表1。
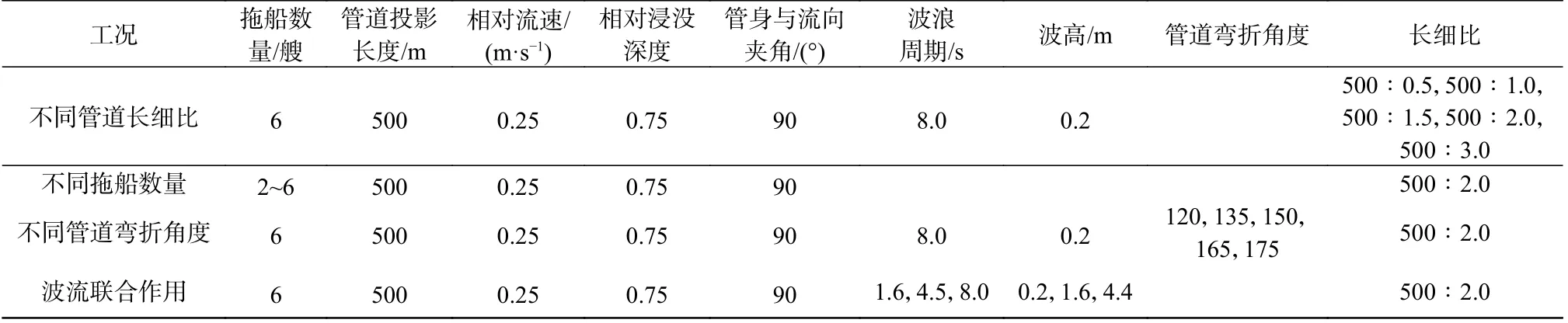
表1 不同工况参数Tab.1 Different working condition parameters
2 管道浮运变形模拟结果分析
2.1 管道长细比对管道变形的影响
依据规范[27],管道许用应力为:[σ]=Kφσs,其中:[σ]为许用应力;K为强度设计系数;φ为焊缝系数;σs为钢材设计强度。本文取K=0.75,φ=0.7,σs=345 MPa,算得许用应力[σ]=181 MPa,换算成应变为860 μm/m。
在水流与波浪的作用下,不同管道长细比对管道变形的影响如图2 所示。从图2(a)和(b)可以看出,在水流的作用下,随着管道长细比增加,管道自身的最大应变与最大位移增加,但是管身应变与位移非同步变化。管身应变峰值出现的规律不明显,管道两端位移较小,中间较大。水流作用下长细比从500∶0.5 到500∶3.0 的管道峰值应变均未超过容许应变值,管道较安全。波浪作用对管道变形的影响如图2(c)和(d)所示,在波浪作用下,管道长细比越大则管道应变和位移均越大,第2 艘拖船与第3 艘拖船之间管身应变和位移峰值最大,拖船数量相同则管身应变峰值出现的位置和次数规律基本相同。类似地,5 种长细比管道在波浪作用下其峰值应变均未超过许用应变值,管道较安全。

图2 长细比对管道变形的影响Fig.2 Influence of slenderness ratio on pipe deformation
2.2 拖船数量对管道变形的影响
在水流作用下,拖船数量对管道的变形影响如图3 所示。从图3 可知,当拖船数量分别为2 艘与3 艘时,管道的最大应变已达5 167.7 和8 270.8 μm/m,远超过许用应变。随着拖船数量增加,管身峰值应变不断减小,拖船数量为4 艘、5 艘、6 艘时管身最大应变为232.5、97.9 和57.4 μm/m。本工况中水流荷载非常小,拖船数量小于等于3 艘时管身应变过大,难以保证管道浮运变形安全。随着拖船数量增加,管道自身最大位移减小。不同拖船数量下管道最大位移出现的位置不同,最大应变位置基本与最大位移出现的位置相同。每增加1 艘拖船管身最大应变或位移约减小一半,说明增加拖船可有效控制管道整体变形。
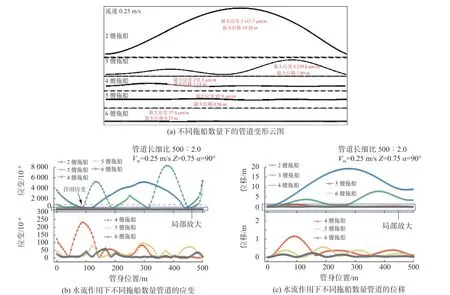
图3 水流作用下拖船数量对管道变形的影响Fig.3 Influence of tugboat number on pipeline deformation under current action
2.3 管身弯折角度对管道变形的影响
管道弯折角度β对管道变形的影响如图4 所示。从图4(a)和(b)可以看出,当管身弯折角等于120°时,管身应变峰值超过容许值,管道可能发生破坏。其余情况管道的应变均小于容许应变值,但当管道弯折角度等于150°时管道最大应变已达到816.42 μm/m,管道有破坏风险。管道弯折角度β越大管身位移越小,弯折角度β为150°时管身最大位移达0.82 m,弯折角度β为120°时管身最大位移达2.31 m。从图4(c)和(d)可以看出,在波浪作用下,管道弯折角度β越大管身应变和位移越小,不同弯折角度的管身应变和位移峰值出现的位置和次数规律在管身前500 m 段大致相同。管身弯折角等于135°和120°时,管身应变峰值超过容许值,弯折角度β为150°时管身最大位移达1.58 m,弯折角度β为135°时管身最大位移达2.37 m,弯折角度β为120°时管身最大位移达2.60 m。以上分析说明,管身弯折角度小于135°不利于管道浮运变形安全,建议在工程设计中应保证管道弯折角度大于135°,且根据实际情况越大越好。
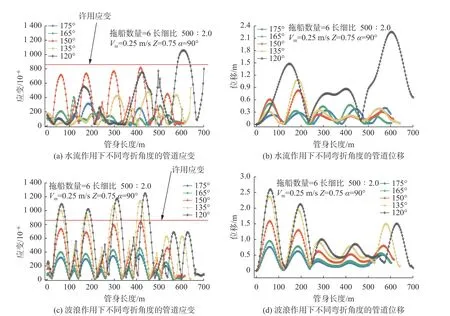
图4 管身弯折角度对管道变形的影响Fig.4 Influence of pipe body bending angle on pipe deformation
2.4 波流联合作用对管道变形的影响
实际浮运状态中波流联合作用下管道的变形如图5 所示,可以看出波流联合作用下管道应变、位移均随波高的增大而增大,随波浪周期的增大而减小,拖船数量相同则管道应变和位移峰值出现的位置和次数规律相同,依据管道容许应变的要求,处于T=1.6 s 和H=4.4 m 波浪条件的管道最大应变超过了容许应变值,处于T=1.6 s 和H=1.6 m 及T=4.5 s 和H=4.4 m 波浪条件的管道应变分别为837.81 和819.70 μm/m,接近容许应变值。故此波浪对管道浮运影响较大,建议在海面平静时进行管道浮运施工,同时也要时刻关注海上环境变化,做好保护措施。
图5 波流联合作用对管道变形的影响Fig.5 Effect of wave-current combined action on pipe deformation
3 厦门某管道浮运施工
厦门某管道工程采用浮运方式施工,管道为两根直径1.6 m,壁厚0.02 m 的Q345 钢质管道,表面有一层3PE 防腐层,管道两端弯折连接陆地,类似倒虹吸管结构形式,管道浮运流程如图6 所示。本文选择管道1 进行模拟计算,管段从顺流向浮运旋转90°至横流向,管道浮运直线距离总长800 m,总路径为1.15 km,管道浮在海面时的中心高程离海底距离最大约为12 m,最小约为4 m。潮流类型为正规半日潮流,湾口最大流速为0.6 m/s,流速范围为0.2~0.4 m/s,强波浪为E 向波浪,平均波高0.19~0.33 m、平均波浪周期1.56~2.06 s、最大波高0.80~1.59 m、最大波周期3.19~4.51 s。
图6 管道浮运流程Fig.6 Pipeline floating flow chart
3.1 管道浮运阻力计算与数值模拟
当管道外径D与波长L的比值即D/L<0.2 时,管道为小尺度结构物,波浪作用下水平管道浮运阻力可以用Morison 方程[28]进行计算。参考陈畅等[29]对漂浮软管在海上波浪力的计算,并进行一定的改进,最终可以得到水平管道波浪阻力计算:
式中:Rw为波浪阻力;Rd为水平拖拽力;Ri为惯性力;Cd为水平拖拽力系数;Cm为惯性力系数;ux为水质点水平速度;∂ux/∂t水质点加速度;h为静水时管道浸没在水中的高度;l为管道长度;A为管身在垂直流向平面上的投影面积;ρ为液体密度。在本次计算中Cd取1.2,Cm取2.0[30]。根据浮运现场波浪条件,波浪周期T= 2.06 s,波高H=0.19m,水深d= 10m,经计算,=2.04 < 6.0,H/d=0.019 <0.2,满足线性波理论,故水质点水平速度和水质点加速度可用下式[31]计算:
式中:z为水质点纵坐标;k为波数;ω为波频。最终计算出波浪阻力最大为671.2 kN。由此可以计算出拖船的配置,拖船数量需大于3 艘,管道首尾各需1 艘,中间需配置辅助拖船,在满足施工要求且节约成本的基础上,暂定拖船数量为4 艘,拖船总拖力应大于671.2 kN。此外还应预留1~2 艘辅助拖船,以便应对突发情况。
3.2 管道浮运变形数值模拟
为模拟浮运状态管道在水流作用下的变形,边界条件设置参考1.1 节,取实际尺寸,具体工况如表2 所示,1 号管道在浮运过程中的变形如图7 所示。

表2 数值模拟实际工况Tab.2 Numerical simulation actual working condition table
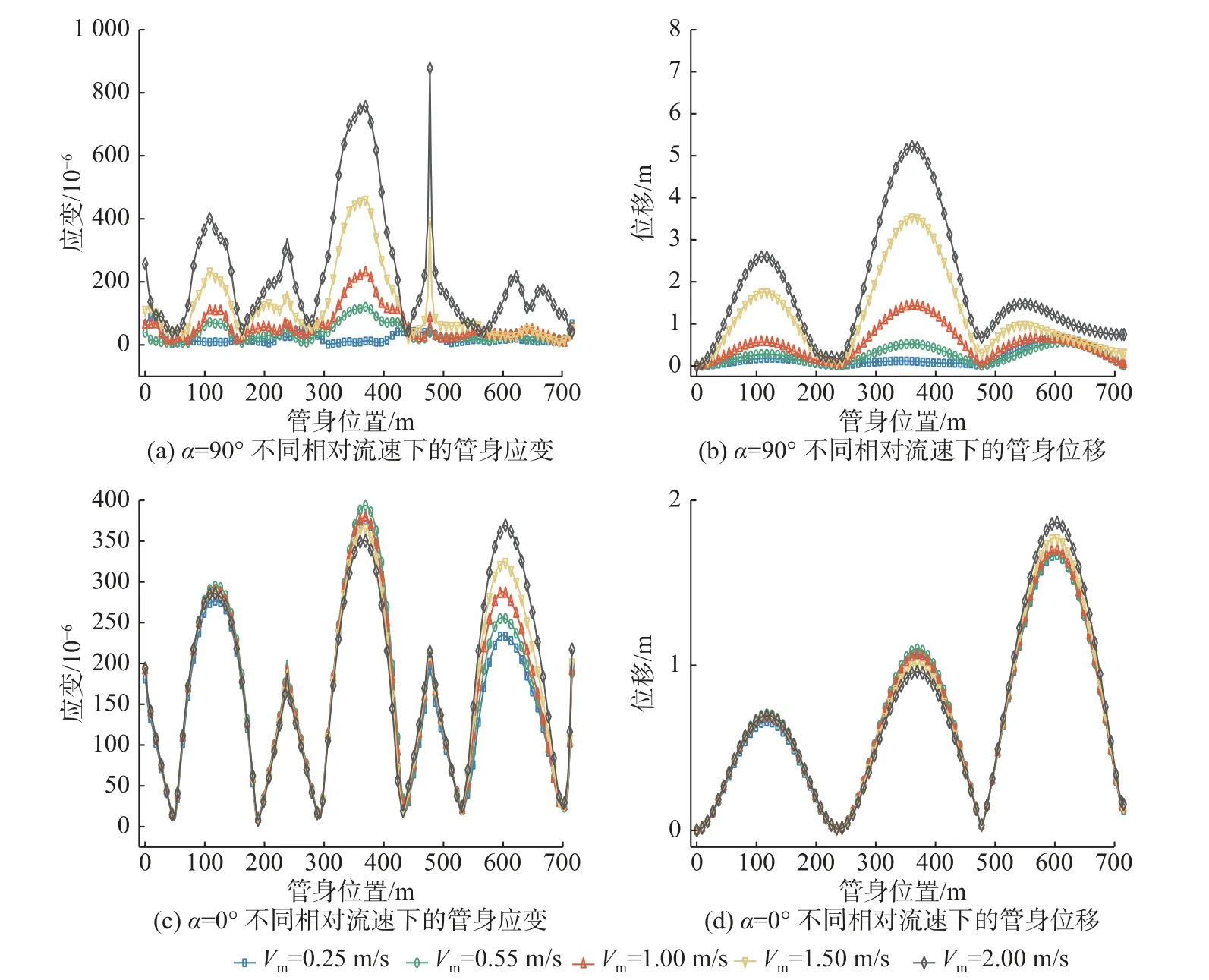
图7 管道浮运变形模拟(拖船4 艘)Fig.7 Simulation data diagram of pipeline floating deformation in Tong’an Bay, Xiamen
从图7(a)可以看出,对于同一管道,当拖船数量相同时,不同相对流速下管身应变峰值出现的次数和位置基本相同。随着相对流速的增加,管身最大应变增大,但是当相对流速为2.00 m/s 时,管身最大应变达877.7 μm/m,超过管道容许应变,说明管道浮运相对速度不宜超过2.00 m/s。从图7(b)可知管身位移随着相对流速的增大而增大,位移峰值出现在两拖船的中间,整个管身跨中位移最大,当相对流速大于1.00 m/s后,管身位移明显增大,当相对流速为2.00 m/s 时管身最大位移达5.22 m。α=0°的管身应变和位移均比α=90°时的小1/2 左右,α=0°时的管身应变和位移的增幅均较小,在相对流速为0.25~2.00 m/s 时管道应变均未超过容许应变,相对来说以角度α=0°来浮运管道更加安全。
3.3 管道浮运现场监测分析
在现场进行浮运实时监测时,由于海上环境潮湿,尤应注意应变片与监测设备的防水问题。为此,在应变片安装完成后,使用环氧树脂胶水加以进一步固定,最后涂抹703 防水胶。使用无线防干扰采集通讯系统DH3819 静态应变采集仪进行浮运过程的应变监测。浮运时,管段1 选取3 个应变监测断面、每个断面布置3 个测点,测点的具体布置如图8 所示,以1 号监测断面为例,测点1-1 为迎水面,1-2 为管道的顶部,1-3 为背水面。
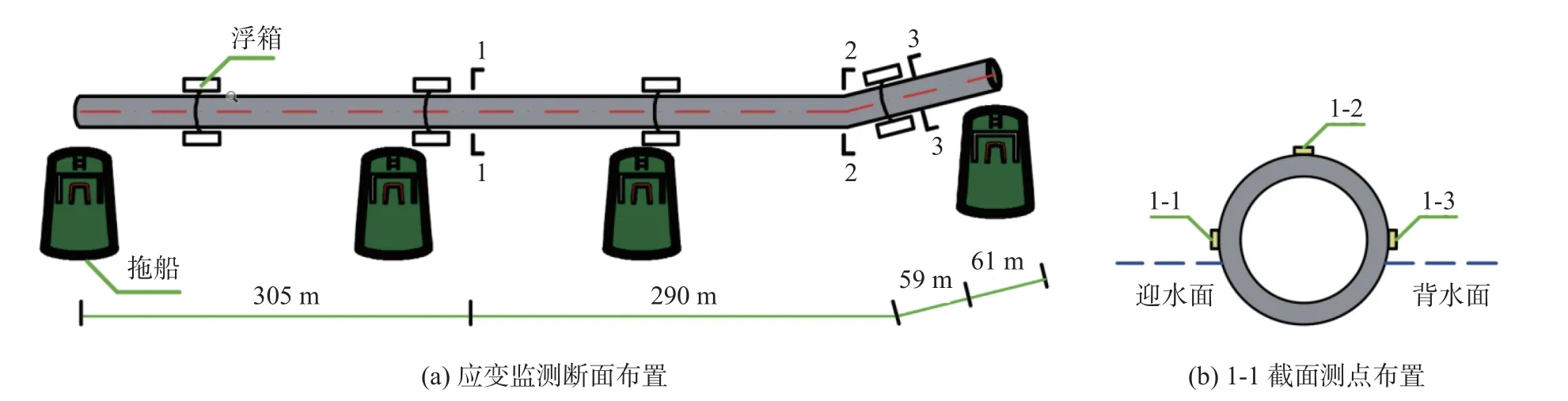
图8 1 号管道测点布置Fig.8 Measuring point layout of No.1 pipeline
浮运时,浮箱与拖船均呈均匀布置。浮运前管身轴线沿着水流方向,风速3.0 m/s,水流流速0.35 m/s,波高0.35 m。浮运开始后,管身以约2°/min 的速度逆时针旋转,经45 min 旋转至垂直于水流方向,在管段1 浮运72 min 后,海面出现6 级风,与管段浮运方向相反,属于逆向风,风速10.5 m/s,水流流速0.55 m/s,波高1.80 m。经110 min 浮运至指定位置。
在旋转浮运过程中,即浮运0~45 min 时,监测断面1 的最大相对流速约为0.58 m/s,最大拉应变为73.9 μm/m,最大压应变为52.5 μm/m;监测断面2 的相应数据为0.42 m/s、73.3 和52.8 μm/m;监测断面3 的相应数据为0.39 m/s、53.4 和41.1 μm/m。在直线浮运过程中,浮运45~72 min 时,1~3 位置的平均相对流速约为0.55 m/s,监测断面1 最大拉应变为77.2 μm/m,最大压应变为28.5 μm/m;监测断面2 的相应数据为70.2 和42.4 μm/m;监测断面3 的相应数据为25.4 和42.8 μm/m。浮运72 min 后,由于风速增大,水流速度激增至0.55 m/s,监测断面1~3 位置的相对流速增加至0.75 m/s,此时监测断面1 最大拉、压应变为151 和122.3 μm/m;监测断面2 的为177.9 和100.4 μm/m;监测断面3 的为85.3 和130.6 μm/m。在1 号管道浮运过程中,应变均小于许用应变且有较大富余。
监测结果与3.2 节中模拟所得结果对比如图9 所示,可以看出当相对水流速度为0.55 m/s 时,在监测截面处的数值模拟与现场监测的应变数值差距较小;当相对水流速度为0.75 m/s 时,由于水流速度激增,应变突增达到预警值,考虑是驳船推力过大所致,故此时监测数据与模拟数据差距较大。立即通知施工单位减小驳船推力,应变随后恢复到正常水平,管道稳定后的各监测截面应变值均处于相对流速为1.00 m/s 时模拟所得应变值以下。这也证明了数值模型的合理性。
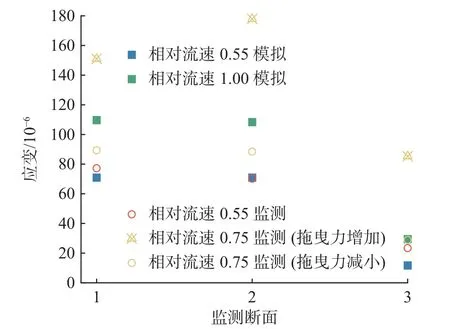
图9 浮运应变监测与数值模拟对比Fig.9 Comparison of floating strain monitoring and numerical simulation
4 结 语
超长管道在海面浮运时,长细比越小、管身弯折角越大、拖船数量越多、相对流速越小、波浪周期越大、波高越小,管身应变和变形越小,浮运越安全。在管道容许应变下,增加拖船数量能有效减小管道变形,波流联合作用时管道变形较大,应选择海上波浪较小时进行管道浮运。建议在实际管道浮运施工中,应保证拖船数量大于3 艘,管身弯折角度大于等于135°。
可以利用改进后的Morison 方程计算管道的波浪阻力,再根据计算结果合理安排拖船数量和浮运速度,确保管道能够成功浮运。相对流速越大管身出现的最大应变也越大,但最大应变位置并非出现在管身同一处,施工前有必要先进行模拟计算,确定施工环境下管身应变最大值及位置并做好保护措施。
