钢筋混凝土结构裂缝宽度计算
2024-01-12戴永琪刘晓青
戴永琪,刘晓青
(1.上海勘测设计研究院有限公司,上海 200434; 2.河海大学 水利水电学院,江苏 南京 210098)
从实际工程中混凝土结构的外观缺陷或表面损伤检测结果可以发现,由于混凝土材料本身较不均匀且抗拉强度较低,钢筋混凝土结构基本处于带缝工作状态。随着外部荷载和环境等因素的持续作用,裂缝不断发展从而影响结构的正常使用和安全运行。因此,对使用上要求限制裂缝宽度的结构构件,如何根据荷载组合进行较为准确的裂缝宽度控制验算,是钢筋混凝土结构设计的重要内容之一。
由于混凝土裂缝的形成机理复杂且影响因素众多,自20 世纪30 年代以来,各国学者提出了许多关于钢筋混凝土结构裂缝宽度的计算式,这些公式大致可分为半理论半经验公式和数理统计公式两类[1-3]。Hong 等[4]针对钢筋混凝土构件在纯弯曲作用下的裂缝宽度预测问题,根据传统裂缝理论和由轴向拉伸试验得到的黏结-滑移关系,分析受拉区钢筋混凝土构件的应力,给出了最大裂缝宽度关于黏结应力的解析式;Oh 等[5]基于钢筋混凝土梁反复加载试验引入了合适的黏结应力与滑移量的函数表达式,通过传递长度和残余滑移量来计算钢筋周围的黏结应力分布,推导出反复荷载作用下的裂缝宽度计算式;朱尔玉等[6]采用三分点加载模式对32 根高强钢筋混凝土梁进行了受弯试验研究,分析其裂缝发展过程和分布规律,对试验数据进行参数回归,得到高强钢筋混凝土纯弯构件的平均裂缝间距和最大裂缝宽度计算式。然而,上述裂缝理论和经验公式都是以一定的假设条件和简化处理为前提,公式之间差异较大,只能粗略估算基本构件的裂缝宽度,不能反映实际工程中的裂缝状态。
近年来,随着计算机技术和钢筋混凝土有限元法的不断发展和完善,基于力学理论的数值模拟与仿真分析成为研究钢筋混凝土裂缝宽度的有效方法。本文针对钢筋混凝土构件实际存在的非线性工作状态,研究钢筋混凝土非线性有限元分析方法,首先基于四参数等效应变混凝土损伤模型确定材料在不同应力状态下的损伤程度,然后根据断裂损伤理论推导混凝土结构的裂缝宽度表达式,最后将所提出的方法应用于四点弯曲钢筋混凝土梁的有限元计算,并与试验结果进行对比分析以验证方法的可行性与合理性。
1 基于四参数等效应变的混凝土损伤模型
首先考虑单轴应力情况,根据损伤力学理论,混凝土在单轴应力状态下的应力应变(σ-ε)关系可以表示为:
式中:Dc为损伤变量,取值范围为[0,1],与混凝土的损伤程度呈正相关;Ec0为混凝土无损时的弹性模量。
由式(1)求得单轴应力状态下混凝土损伤变量的表达式为:
本文采用文献[7]中混凝土单轴拉伸试验拟合得到的应力应变曲线,该本构关系曲线分为上升段和下降段:
式中: σp为峰值拉应力; εp为峰值拉应力时的应变。
对于多轴应力情况,通过对各应变分量的适当组合引入等效于单轴拉伸或压缩状态下的应变,可以根据单轴拉压时的损伤演变方程得到多轴应力状态下的损伤变量值。根据文献[8]可得四参数等效应变:
求解式(4)即可得到多轴应力状态下的等效应变:
由于等效应变不可能为负值,因此只取式(5)的正根:
参考Hsieh-Ting-Chen 应力空间四参数破坏准则的形式,建立基于应变空间的四参数破坏准则:
由式(7)可知,参数A、B、C、D可通过单轴拉伸、单轴压缩、双轴等压及三轴压缩等4 组强度试验数据来确定,再将求得的4 个参数值代入式(6)即可计算等效应变。
式中:ε1、ε2、ε3分别为3 个主应变;E为弹性模量; µ为泊松比;ft、fc分别为混凝土的单轴抗拉强度和单轴抗压强度。
钢筋混凝土由两种不同性质的材料组合而成,除了建立合理的混凝土本构关系外,如何正确模拟钢筋和混凝土的组合作用也是按有限元法分析结构各阶段工作状态、受力情况和变形响应的关键。
分离式模型是研究钢筋与混凝土间相互作用时较为常用的有限元模型,优点是可以用联结单元模拟材料实际存在的黏结特性和相对滑移,但传统的双弹簧联结单元在选择其法向刚度系数时,取值过小会使单元相互嵌入产生偏差,取值过大又可能导致计算不收敛。因此,本文采用改进的单弹簧联结单元法,只在钢筋切向设置单弹簧,通过建立钢筋与混凝土法向自由度的约束方程保证两者间的法向变形协调,以避免人为设定法向刚度系数。
2 基于断裂损伤理论的裂缝宽度计算
钢筋混凝土有限元法中常用的裂缝模拟方法主要有分离裂缝模型、弥散裂缝模型和断裂力学裂缝模型3 种,弥散裂缝模型以分布裂缝代替单一裂缝,通过调整材料的本构关系来模拟混凝土的开裂过程,具有计算精度高和运算速度快等优点,也避免了分离裂缝模型由于裂缝的出现和延伸需要不断重新划分单元网格的不便,因而在各种复杂组合构件和非杆件大体积混凝土结构的裂缝分析中得到广泛应用[9]。但传统的弥散裂缝模型实质上是将裂缝弥散分布到整个单元中,保持了混凝土结构位移场连续的假定,而没有模拟单元边界之间实际存在的非连续开裂面,导致难以确定裂缝宽度和分布间距等信息。针对上述问题,首先基于弥散裂缝模型和裂缝带理论[10],将混凝土单元内的裂缝宽度在单元特征长度范围内弥散成开裂应变,假设该应变沿断裂带宽度方向均匀分布,则裂缝宽度可表示为:
式中:w为裂缝宽度;le为单元特征长度; εcr为开裂应变。
混凝土属于准脆性材料,拉应力达到抗拉强度后会呈现一定的软化现象,拉应力随裂缝开展宽度的增加而逐渐减小[11]。为了合理控制验算结构的裂缝宽度,需要在考虑混凝土软化特性的基础上进行裂缝分析。断裂能是描述混凝土开裂软化过程的重要参数,可以根据混凝土软化曲线与坐标轴围成的面积求得:
式中:Gf为混凝土断裂能;wf为材料完全开裂时拉应力下降至零对应的极限裂缝宽度; σ为拉应力;gf为混凝土开裂应变能; εf为材料完全开裂时拉应力下降至零对应的极限开裂应变,由式(12)可知εf=wf/le。
当采用单直线下降式软化曲线来描述混凝土的软化行为时,由式(13)和式(14)可得材料的极限裂缝宽度和极限开裂应变分别为:
由式(15)和(16)可知,极限裂缝宽度和极限开裂应变同断裂能和开裂应变能一样,是反映混凝土材料物理力学性能的参数,与试件的形状和尺寸无关。当混凝土的裂缝宽度和开裂应变达到极限值时,裂缝尖端处的拉应力下降至零,微裂纹继续扩展并相互连通形成宏观裂缝。因此,对使用上不允许出现裂缝的钢筋混凝土构件,可将上述公式的计算结果作为限值,但还需进一步推导混凝土损伤开裂过程中产生的最大裂缝宽度计算式才能进行抗裂验算;对使用上要求限制裂缝宽度的构件,最大裂缝宽度限值应根据混凝土结构所处的环境条件类别来确定,但也需要计算结构在服役过程中产生的最大裂缝宽度才能进行裂缝宽度验算。下面进行具体说明。
真实场景下的裂缝会将混凝土划分为未开裂区和开裂区,但在损伤力学和弥散裂缝理论中这两个区域都处于连续场中,采用应变分解方法将混凝土总应变分解为弹性未开裂应变和非弹性开裂应变:
式中: ε为混凝土单元的总应变; εc0为未开裂部分材料的弹性应变,假定未开裂区混凝土满足线弹性本构关系,再结合混凝土损伤模型中的应力应变关系式(1),可得:
将式(18)代入式(17),可知开裂应变与总应变之间满足以下关系式:
再将式(19)代入式(12),得到混凝土损伤开裂过程中的裂缝宽度及其最大值为:
式中:wmax为最大裂缝宽度;εmax为最大总应变。
需要注意的是,式(12)~(20)是在假设1 个单元内只有1 条裂缝的前提下推导的,适用于有限元网格划分较密的情况。对于复杂的大体积混凝土结构,在满足计算精度和考虑求解效率的条件下网格加密程度有限,这就导致1 个单元内可能存在多条裂缝。为解决上述问题,设1 个单元内的裂缝数量为n,每条裂缝的张开度均为w,则根据式(12)可以求得单条裂缝宽度的表达式为:
式中:lm为平均裂缝间距。
由式(13)~(16),可得如下公式:
将式(19)代入式(21),得到1 个单元内存在多条裂缝时混凝土损伤开裂过程中的裂缝宽度及其最大值分别为:
最后考虑多轴应力情况,在建立四参数等效应变和应变空间四参数破坏准则的基础上,可以根据单轴拉压时的损伤演变方程得到多轴应力状态下的损伤变量值。通过四参数等效应变替换普通单轴应变,并结合单轴应力情况下混凝土损伤开裂过程中的裂缝宽度表达式,即可计算混凝土结构在多轴应力状态下的最大裂缝宽度,其表达式为:
3 算例验证
3.1 计算模型及参数
为验证上述钢筋混凝土非线性有限元分析方法的合理性,选取文献[12]中用于受弯性能试验的钢筋混凝土简支梁进行数值模拟计算,该四点弯曲梁的几何尺寸和配筋见图1。试验梁长8 000 mm,宽350 mm,高700 mm,保护层厚35 mm。混凝土强度等级为C40,抗拉强度2.8 MPa,抗压强度30.2 MPa,弹性模量33.848 GPa,泊松比0.2,求得4 个参数分别为A=0.011 8,B=0.099 6,C=0.740 0,D=0.308 9,混凝土断裂能为130.32 N/m。受拉主筋为直径20 mm 的HRB500 钢筋,屈服强度537 MPa,弹性模量200.546 GPa,配筋率0.68%;架立筋和腰筋采用直径为12 mm 的HRB400钢筋;箍筋为直径8 mm 的HRB400 钢筋,纯弯段箍筋的间距为300 mm,其余段箍筋的间距为150 mm。
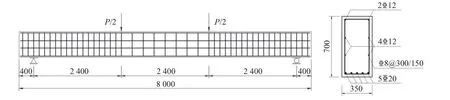
图1 试验梁尺寸及配筋示意(单位:mm)Fig.1 Diagram of dimension and reinforcement of test beam (unit: mm)
根据以上基本信息建立四点弯曲钢筋混凝土梁的分离式有限元模型,混凝土梁及其加载和支座处的钢垫板用实体单元模拟,钢筋用杆单元模拟,在钢筋和混凝土之间设置单弹簧联结单元,如图2 和图3 所示。

图2 混凝土梁有限元模型Fig.2 Finite element model of concrete beam
图3 梁中钢筋模型Fig.3 Reinforcement model in beam
3.2 计算结果分析
图4 给出了采用单弹簧联结单元法和混凝土四参数损伤模型计算得到的四点弯曲梁跨中弯矩-挠度曲线,该曲线清晰反映出钢筋混凝土梁从加载到破坏全过程中所经历的3 个典型阶段的主要特征和变化规律,并且数值模拟结果与试验数据较为吻合。在加载初期,由于弯矩较小受拉区未开裂,混凝土处于弹性工作阶段,拉应力由混凝土和钢筋共同承担,梁跨中弯矩和挠度之间近似呈线性关系,挠度计算值与试验值基本相同。当持续加载达到开裂弯矩时,部分受拉区混凝土退出工作,弯矩-挠度曲线出现第1 个转折点,标志着混凝土梁进入裂缝开展阶段,开裂截面处的拉应力几乎全部由受拉钢筋承担,跨中挠度明显增大。加载至钢筋拉应力达到屈服强度时,弯矩-挠度曲线出现第2 个转折点,标志着混凝土梁进入破坏阶段,这一阶段的挠度增长速度更快,曲线斜率进一步减小,直到构件完全破坏。该四点弯曲钢筋混凝土梁的实测极限弯矩值为614 kN·m,计算值为616 kN·m。
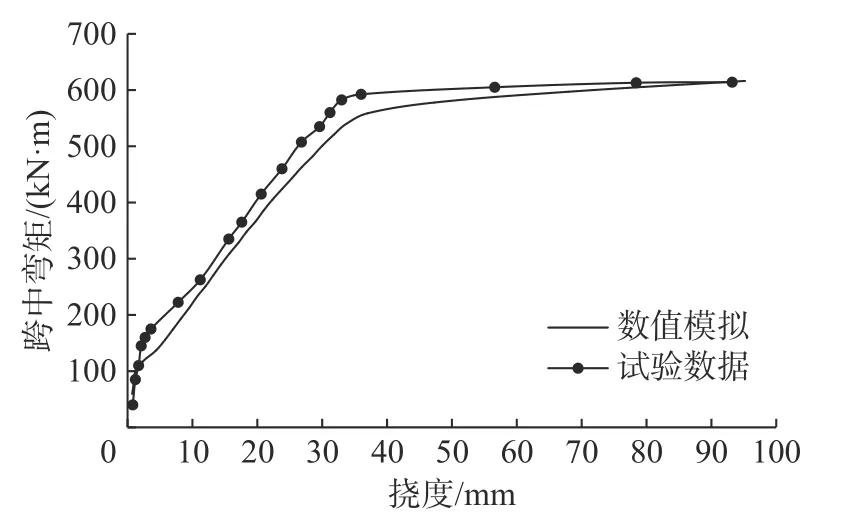
图4 跨中弯矩-挠度曲线Fig.4 Moment-deflection curve at midspan
由式(26)可知,损伤变量值与混凝土的损伤开裂程度呈正相关。图5 为该四点弯曲钢筋混凝土梁在加载过程中的裂缝发展规律和分布特征。从图5 可以看出,构件开裂后首先在加载点之间的纯弯段底部产生竖向裂缝,之后向上扩展,并有新的裂缝在纯弯段和剪弯段出现,裂缝间距不断减小,随着荷载继续增加,纯弯段竖向裂缝的数目、高度和间距都趋于稳定,而剪弯段竖向裂缝逐渐向加载点位置延伸从而形成斜裂缝,上述裂缝开展过程与试验现象一致。

图5 四点弯曲梁在加载过程中的损伤分布Fig.5 Damage distribution of four-point bending beam during loading
基于损伤变量和等效应变计算得到的最大裂缝宽度变化曲线见图6,与试验数据的符合程度较高,误差在8%以内;而按《混凝土结构设计规范》(GB 50010—2010)计算的最大裂缝宽度总体偏大,与数值模拟结果和实测值相差5%~45%,且加载中期偏差较大,说明规范公式在计算高强钢筋混凝土梁的最大裂缝宽度时的部分参数需进一步修正。由图6 可知,当荷载小于245 kN 时,荷载与裂缝开展宽度之间近似呈线性关系,由于钢筋拉应力还未达到屈服强度,此时的最大裂缝宽度仍处于稳定增长阶段,但随着荷载进一步增加,钢筋屈服后应变迅速增大,导致裂缝急剧开展并向上延伸。
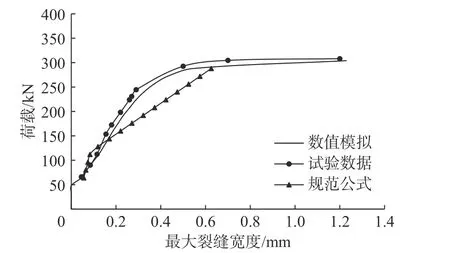
图6 荷载-最大裂缝宽度曲线Fig.6 Load-maximum crack width curve
4 结 语
本文对钢筋混凝土结构的裂缝宽度计算进行研究,主要结论如下:
(1)极限裂缝宽度和极限开裂应变同断裂能和开裂应变能一样,是反映混凝土材料物理力学性能的参数,与试件的形状和尺寸无关。当混凝土的裂缝宽度和开裂应变达到极限值时,裂缝尖端处的拉应力下降至零,微裂纹继续扩展并相互连通形成宏观裂缝。对使用上不允许出现裂缝的钢筋混凝土构件,可将极限裂缝宽度的计算结果作为限值进行裂缝控制验算。
(2)建立包括混凝土四参数损伤模型和裂缝宽度-等效应变关系式在内的钢筋混凝土非线性有限元分析方法,适用于求解混凝土结构在复杂多轴应力状态下的损伤变量和裂缝宽度。以四点弯曲梁为例进行有限元计算,可以细致描述钢筋混凝土梁从加载到破坏整个受力过程中的变形特征和开裂规律。
(3)算例分析表明,四点弯曲钢筋混凝土梁的损伤分布与试验现象基本一致,最大裂缝宽度变化曲线也与实测数据的符合程度较高,验证了计算模型的合理性和准确性。
