网络攻击下电力系统的离散迟滞量化控制

谢佳杰, 宋公飞, 杜 鹏

(1.南京信息工程大学 自动化学院,江苏 南京 210044; 2.南京信息工程大学 江苏省大气环境与装备技术协同创新中心,江苏 南京 210044)

量化控制作为控制工程领域的前沿热点问题,受到广大科研工作者的关注。在网络控制的应用中,系统设备之间的信息通过通信网络在离散时间使用数据包传输,这个过程通常占用大量的网络资源,例如网络带宽、计算能力等[1]。因此量化控制在网络控制中扮演着举足轻重的角色,其作用是通过量化器将接收到的连续信号近似为有限多个离散值,从而减少控制器接收信号所包含的信息,但是又不使输入信号失真[2]。因此将量化控制应用于网络系统的想法顺其自然地产生了。然而随着网络化系统的应用与发展,单独的量化控制并不能完全满足信息传输的要求,因此,考虑在量化控制的基础上对系统进行离散化处理,进一步减少网络系统中传输信号所包含的非必要信息,从而降低网络通信压力。

近年来网络系统抵抗网络攻击的能力,即网络系统的稳定性成为研究的热点[3]。为了使系统稳定并且尽可能降低网络通信压力,许多学者选择设计量化反馈控制器,取得了很多有意义的成果。例如文献[4]研究了当网络系统遭到欺骗攻击时系统的预测控制并且给出了系统稳定的条件。文献[5]研究了随机非线性系统在遭到网络欺骗攻击时基于离散观测的安全控制问题,建立了矩阵不等式形式的充分条件,保证了预先确定的概率安全性。文献[6]提出了一种对数量化反馈控制器的几何设计方法,此方法适用于处理一类非线性系统。文献[7]在网络系统中应用对数量化器对传输信号进行量化并且考虑了系统受到网络欺骗攻击时是否能够保证稳定的问题。对数量化器易产生抖震现象,不利于系统的稳定,因此文献[7]给出了一个新的迟滞量化器,利用自适应控制反步法研究一类具有量化输入的非线性不确定系统。文献[8]同样运用反步法设计了控制器,但是其提出文献[7]设计的稳定条件具有特殊性。因此,为了解决这一问题,文献[9]针对具有迟滞量化输入的严格反馈系统,研究了一种基于反推的自适应稳定方法。但是文献[7]和文献[8]都是基于不确定的非线性是已知函数,其参数未知并且对于这些已知函数是线性的,同时非线性函数满足全局Lipschitz条件。文献[10]和文献[11]提出了一种具有量化输入信号的随机严格反馈非线性系统的模糊自适应方法,文献[11]同时考虑了不确定非线性和未知的随机扰动,并且对量化输入提出一种新的非线性分解,建立了控制信号与量化信号之间的关系。随着对迟滞量化器的深入研究,在网络控制以及非线性自适应控制方面取得了显著进步,其中利用反步控制算法设计自适应控制器的策略更是成为解决非线性系统控制问题的一个突出方向[11-13]。此外,文献[14]研究了受多面体类型不确定性影响的离散时间马尔可夫链驱动的系统和受时滞影响的非线性随机系统,同时提出了线性矩阵不等式理论来设计反馈控制器。文献[15]提出了基于离散状态和模式观测的混合随机系统加以鲁棒量化控制的方法,从而减少网络通信的负担,降低信号传输的丢包率。结合以上文献,在网络混杂随机系统中,采用基于状态和模态离散观测的迟滞量化反馈控制,能够进一步提高网络通信效率并保证系统的稳定性。

由于电力系统十分重要并且具有实际意义,因此针对电力系统研究出了许多控制方法。例如文献[16]针对舰船综合电力系统,利用改进蝙蝠算法优化控制器的模糊规则,加快自适应控制速度。文献[17] 设计了一种基于逻辑开关控制的切换控制器并从理论上证明了切换控制器与被控系统组成的闭环系统的稳定性。以上控制并不能有效解决网络通信过程中数据过多的问题,因此,本文设计的离散迟滞量化器能够降低网络通信压力。

本文的主要创新点如下:

① 在网络系统中首次采用迟滞量化反馈控制,建立了网络欺骗攻击下随机网络系统的数学模型,其中发生与未发生网络欺骗攻击的数学模型通过伯努利随机变量组合在一起。

② 将迟滞量化反馈控制器应用于离散观测系统中,进一步降低了控制成本,节约了通信资源,并且通过应用迟滞量化器,消除了对数量化器带来的抖震现象。

③ 将离散观测应用于网络系统中,减少了网络节点接收的信号,同时又保证接收到的信号不失真,从而提高了网络资源的利用率、减轻了网络信号传输时的通信压力。

1 系统描述及预备知识

1.1 系统描述

考虑如下具有不确定结构的电力系统随机网络控制模型:

dx(t)=[(A(r(t))+ΔA(t,r(t)))x(t)+u(x([t/τ]τ),

r([t/τ]τ))+C(r(t))g(x(t),r(t))]dt+

(1)

式中:x(t)为状态变量;r(t),t≥0为概率空间上的右连续马尔可夫链,取有限状态空间S={1,2,…,N}中的值;ω(t)=[ω1(t)ω2(t) …ωn(t)]为m维布朗运动;u(x([t/τ]τ),r([t/τ]τ))为控制输入,控制输入以如下形式表现:

u(x([t/τ]τ),r([t/τ]τ))=
E(r(t))qr(t)(K(r([t/τ]τ))x([t/τ]τ))

式中:E(·),K(·)为给定的具有适当维数的参数矩阵;qr(t)为模态相关的迟滞量化器;生成元Γ=(γij)N×N由下式得:

ΔA(t,i)=LaFa(t)NAi, ΔBk(t,i)=LbFb(t)NBki

(2)

式中:La,Lb,NAi,NBki为已知实常数矩阵并且Fa(t),Fb(t):R+→Rs×t为实值时变矩阵满足:

Fa(t)TFa(t)≤I,Fb(t)TFb(t)≤I

(3)

式中:I为单位矩阵。

通过文献[1]的启示,考虑网络攻击模型为

(4)

式中:φ(t)=[t/τ]τ,[t/τ]τ是t/τ的整数部分;0≤ψ(t)≤1是随机分布的伯努利变量;fi(x(φ(t)))为网络欺骗攻击信号,满足[18]:

‖fi(x(t))‖≤‖Yx(t)‖

(5)

式中:Y为一个已知正定矩阵。

因此,可以得到控制输入为

(6)

系统中的g(x(t),r(t))gi(x(t)):Rn×S→Rn为可微非线性函数,并有如下假设。

假设1[18]:假设gi(x(t))是关于x(t)的全局Lipschitz函数,如果|gi(0)|=0并且:

|gi(x1(t))-gi(x2(t))|≤ζ|x1(t)-x2(t)|

(7)

式中:ζ>0称为Lipschitz条件,则具有离散控制器的系统(1)可以表示为

dx(t)=[(A(r(t))+ΔA(t,r(t)))x(t)+

E(r(t))qr(t)(K(r([t/τ]τ))×

(ψ(t)fi(x(φ(t)))+(1-ψ(t))x(φ(t))))+

ΔBk(t,r(t))]x(t)dωk(t)

(8)

式中[19]:

(9)

(10)

式中:Di、Mi、Tgi、Tchi、σi、Ri分别为区域i内的阻尼系数、惯性常数、调速器的时间常数、涡轮常数、频率偏置常数、跌落特性。

1.2 迟滞量化器

本文中采用迟滞量化器来避免抖震现象。抖震是一种高频振荡,在对数量化器中,假设控制信号u在量化边沿Q附近发生振荡(以先减小后增大再减小为例),如图1所示,q(u)将在量化级别RM和PQ之间高频振荡,即R→Q→R,从而引发了抖振现象。

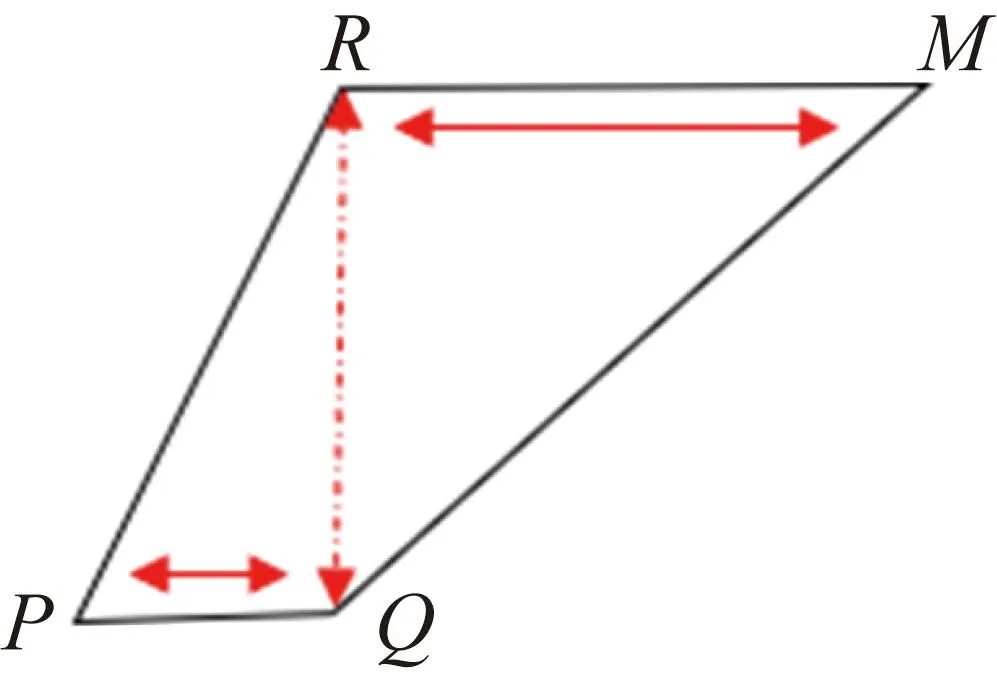
图1 对数量化局部曲线

为了避免抖振现象,采用迟滞量化器的量化方法。迟滞量化器采用2个量化密度相同但量化值不同的量化器,分别为量化器1和量化器2。同一时间只有一个量化器在工作,当量化器切换时,量化值变化。

在迟滞量化器中,假设控制信号u在量化边沿R附近发生振荡(以先减小后增大再减小为例),如图2所示,开始时量化信号q(u)位于量化器1的量化级别RM的Rc上,当u减小到小于量化边沿R时,q(u)从量化器1的量化级别RM上切换到量化器2的量化级别NJ并处在Nb上;当u增大时,q(u)从量化器2的量化级别NJ切换到量化器1的量化级别PQ并处在aQ上;当u增大到大于量化边沿Q时,q(u)从量化器1的量化级别PQ切换到量化器2的量化级别NJ并处在bJ上;当u再次减小时,q(u)从量化器2的量化级别NJ切换到量化器1的量化级别RM并处在Rc上,回到量化边沿R处。整个过程即Rc→Nb→aQ→bJ→Rc。

图2 迟滞量化局部曲线

对比对数量化器和迟滞量化器在u发生振荡时,对数量化器的量化值是2个值直接变化,而迟滞量化器的量化值历经多个值的变化,这种变化为量化值q(u)的变化提供了停留时间,可以看作是为量化器添加滞后的方法,避免了抖振现象。

迟滞量化器在文献[20]中被首次提出。模态相关的迟滞量化器形式如下:

(11)

量化器qi(u(t))以类似于文献[8]和文献[21]的形式表示迟滞量化器:

(12)

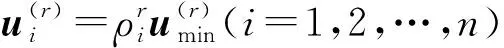
引理1[22]:为了达到应用迟滞量化器控制的目的,将迟滞量化器分为线性部分与非线性部分,表达形式如下:

q(u)=u(t)+D(t)

(13)

式中:D(t)=qi(u(t))-u(t)∈ℜ1。

非线性部分D(t)满足以下不等式:

(14)

(15)

2 控制器设计

在继续推导之前,给出如下引理,这些引理将用于证明系统(1)是均方指数稳定的。

引理2[15]:对任意的t≥0,v>0和i∈S,满足:

(16)

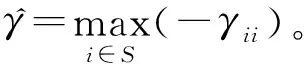
引理3:设x(t)为系统(1)的解。

并且定义:

h(τ)=(8τ2Ma+8τ2ζ2+8τMb+4τ2Y2MK)×

e8τ2Ma+8τ2ζ2+8τMb,τ>0

(17)

H(τ)=(8τ2Ma+8τ2ζ2+8τMb+4τ2MK)×

e8τ2Ma+8τ2ζ2+8τMb,τ>0

(18)

F(τ)=64τ2Mu(τ2Ma+τ2ζ2+τMb)

e8τ2Ma+8τ2ζ2+8τMb,τ>0

(19)

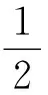
(20)

(21)

(22)

下文继续讨论基于离散时间状态和模式观测的迟滞量化反馈控制器位于控制器到执行器侧时,系统(1)的稳定性问题。

定理1:当发生网络攻击时,假设存在矩阵Ki>0、Qi>0以及正定标量βi,ε,ζ,β2i,ηi(i∈s)使下列式子

(23)

如果τ足够小,满足:

(24)

那么系统(1)满足:当u(s)≥umin,ψ(t)=1时,

(25)

即被控系统(1)在受到网络攻击时是均方指数稳定的。

dV(x(t),r(t))=LV(x(t),r(t))dt+dM1(t)

式中:M1(t)为满足M1(0)=0的鞅并且:

LV(x(t),i)=2x(t)TQi[(Ai+ΔAi(t))x(t)+

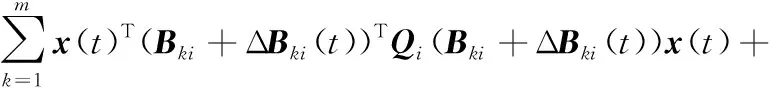
通过假设1可得:

2x(t)TQi[(Ai+ΔAi(t))x(t)+

2x(t)TQiEiD(t)

(26)

推论1:当系统(1)遭遇网络攻击并且输入信号大于死区,即当u(s)≥umin,ψ(t)=1时,

(27)

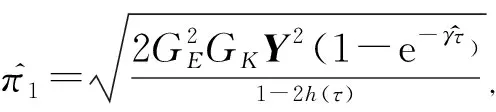
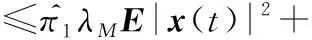
(28)

同式(27),可将2x(t)TQiEiD(t)项放缩为

(29)

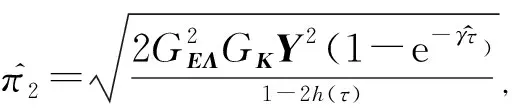
(30)

通过计算可得:

我们发现，为加强与离院后病人的沟通联系，朋友和直系亲属的姓名、地址，而非目前家庭的信息，对于保持与病人的联系是十分有价值的。

(31)

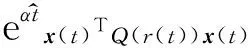
(32)

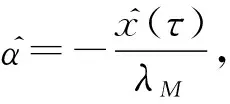
=λME|x(0)|2

(33)

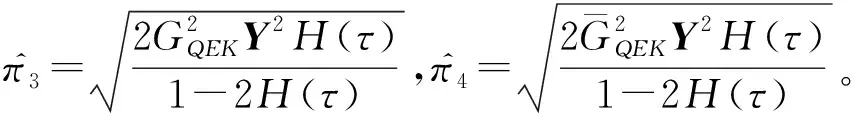
定理2:当没有发生网络攻击时,假设存在矩阵Ki,Qi>0以及正定标量βi,ε,ζ,β2i,ηi(i∈s)使下列两式:

(34)

(35)

(36)

(37)

那么系统(1)满足:当u(s)≥umin,ψ(t)=0时,

(38)

当u(s)≤umin时,

(39)

即被控系统(1)在未受到网络攻击时是均方指数稳定的。

2x(t)TQiEiK(r(φ(t)))x(φ(t))
≤x(t)T(Sym{QiEiKi})x(t)+
2GQEK|x(t)|×|x(t)-x(φ(t))|-
2x(t)TQiEi(Ki-K(r(φ(t))))x(φ(t))

(40)

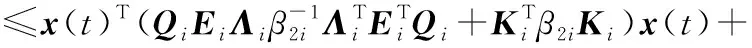
(41)

-2E[x(t)TQiEi(Ki-K(r(φ(t))))x(φ(t))]
≤2π1λME|x(t)|2

(42)

(43)

同定理1可得:

d[eαtx(t)TQ(r(t))x(t)]=eαt(αx(t)TQ(r(t))x(t)+

LV(x(t),r(t)))dt+dM3(t)

(44)

eαtE[x(t)TQ(r(t))x(t)]≤λME|x(0)|2

(45)

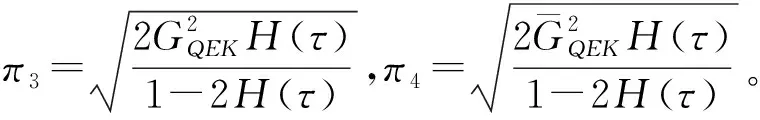
同样的方法可以推导得出式(39)成立。因此,综合定理1与定理2可得,被控系统(1)无论是否遭遇网络攻击都是均方指数稳定的。

3 仿真实验

考虑网络攻击下电力系统(8)具有以下参数[24]:

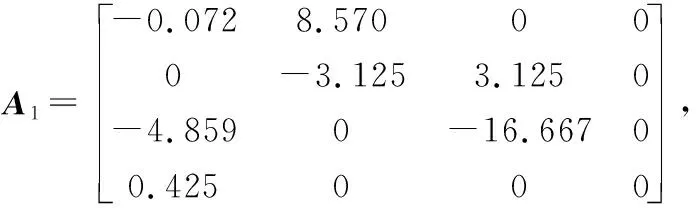
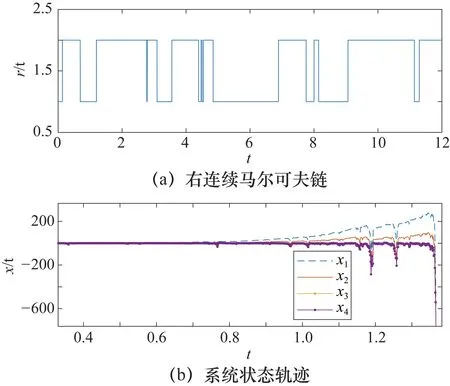
图3 开环系统的轨迹

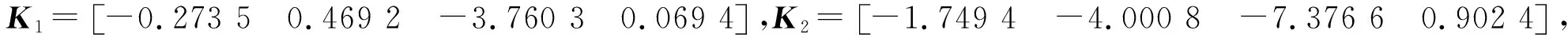
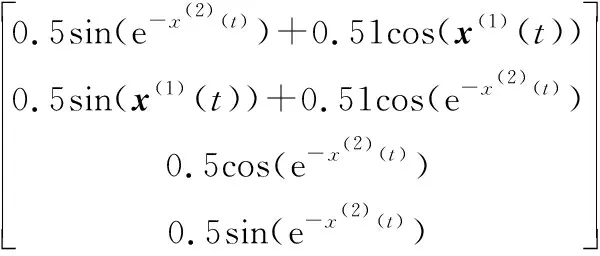
当闭环系统(1)遇到网络欺骗攻击时闭环系统的轨迹如图4所示。

图4 欺骗攻击发生时闭环系统的轨迹

由图4可以看出当网络系统遭到网络欺骗攻击时,基于离散观测状态和模态的迟滞量化控制器仍然能够保证随机网络系统的稳定性。

闭环系统(1)未受到网络欺骗攻击时的仿真结果如图5所示。

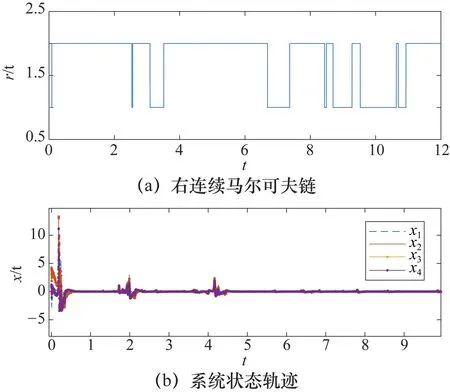
图5 状态反馈:闭环系统的轨迹

由图5可以看出无网络欺骗攻击时,闭环系统在遭到随机网络波动时,仍然能够保证系统的稳定性。

4 结束语

针对随机网络系统,研究了状态和模态离散的迟滞量化反馈控制问题。设计的控制器能够保证被控系统无论是否受到网络欺骗攻击都是均方指数稳定的。仿真结果也表明本文提出的控制方案是有效的。接下来的工作主要有两个方向:首先网络攻击是随机发生的,在保证无网络攻击时系统稳定的条件下,可以考虑将事件触发机制加入,研究网络攻击下离散状态的随机网络控制系统的事件触发控制,通过该方法进一步节约随机网络控制资源;其次考虑网络受到欺骗攻击与拒绝服务攻击时,如何增加系统的普适性。