轿车翼子板屈曲抗凹性能分析及优化

于佳鑫

（长春汽车工业高等专科学校，长春 130013）

0 引言

汽车覆盖件是指构成汽车车身或驾驶室、行李舱等的金属板件，是汽车的重要组成部分。汽车覆盖件的质量指标主要包括以下几个方面：尺寸精度、表面质量、力学性能、金相组织、焊接质量、装配质量和耐腐蚀性等。在设计生产时，要符合工艺要求和产品标准，以保证汽车的安全性和使用寿命。

翼子板是遮盖车轮的车身外板，是安装在汽车车轮周围的金属板，主要作用是防止车轮在行驶过程中溅起的泥土、石子等杂物飞到车身和其他车辆上，同时也可以保护车轮和制动系统不受外界杂物的侵害。翼子板在设计时要保证前轮转动及跳动时的最大极限空间，因为其所处特殊位置，在使用中容易受到外载荷的作用，如人为接触按压等，使其局部凹陷或产生永久变形。

屈曲分析主要是一个涉及结构力学的问题，主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷。其基本原理是计算结构在给定载荷下的弹性变形和应力分布，并确定结构的屈曲模态和屈曲载荷[1]。本文针对某车型翼子板屈曲抗凹性能进行分析，对其优化方案进行论证，最终达到目标要求。

1 有限元模型建立

有限元模型的前处理是有限元分析的关键步骤之一。建立有限元模型首先要确定研究对象，包括其几何形状、边界条件和材料属性等。其次是划分单元，也就是将研究对象划分为若干个单元，每个单元由若干个节点组成。单元的形状和大小应该根据研究对象的几何形状和受力情况来确定。在划分单元之后，需要定义每个节点的坐标和自由度。节点的自由度取决于研究对象的运动方式和约束条件。最后是定义单元属性，如弹性模量、泊松比等。

翼子板有限元模型主要是车身外板翼子板部件，通常采用壳单元模拟。壳单元是一种用于模拟薄壁结构的有限元单元，它是一种二维结构单元，通常用于模拟平板、壳状结构和管道等具有一定厚度的结构。其特点是在其厚度方向上的变形相对较小，而在平面内的变形相对较大。因此，壳单元可以有效模拟结构的弯曲、扭转、拉伸和压缩等变形。其计算效率高，可以有效地减少计算时间和计算成本。同时，还可以有效地模拟结构的局部变形和应力集中等问题[2]。

网格划分是将物理模型划分为有限个单元的过程，后期再进行数值计算和模拟。网格划分是数值计算和模拟的基础，它决定了计算的精度和效率。如果网格划分的质量不好，可能会导致精度、收敛性、计算时间和结果可靠性等问题。

翼子板有限元模型的模型网格尺寸采用10.00 mm×10 .00 mm建模。三角形单元所占比例低于5%，翘曲小于10%。在前处理软件中导入相应的翼子板CAD 模型，划分网格，并按照相应要求更改PID 以及ID。给划分后的网格赋予属性以及材料，外板材料及厚度为DC54D+ZF45/45_0.70 mm（图1）。

图1 有限元模型

2 边界条件

翼子板的屈曲抗凹分析考虑了几何、材料及接触的非线性。通常在结构力学分析中，默认为几何线性。即在几何线性设置中，平衡方程是在未变形状态下建立的，并且不会随变形而更新。在分析中材料具有非线性的应力和应变关系。在分析中采用的是直径80.00 mm，一端封闭的柱状板壳压头，并在刚性面与翼子板之间建立接触关系，来传递垂直接触表面的力。

打开HyperMesh 软件，选择Abaqus Standard3D 模板，进入Abaqus 隐式分析模板。导入翼子板的.inp 文件或直接打开.hm文件，进行压头模型的输入及边界条件的编辑。压头可以通过CAD 软件画出来几何形状，在HyperMesh 软件中划分网格。也可以将压头单独存成.inp 文件，以便后期在计算抗凹分析中使用。

将压头文件带入后调整压头在翼子板上的位置，使之移动到合适的位置。使用Tool>position 能调整压头位置。点击压头所在层，“from”选择的N1、N2、N3 这三点是压头下表面上的点，“to”选择的N1、N2、N3 三点是翼子板上的要分析部分的点。保证from 与to 的方向一致性。

约束翼子板与车身安装点全部自由度1、2、3、4、5 和6，如图2 所示。由于翼子板造型曲率较大，受到外部载荷时，容易发生屈曲的风险，因此选择隐式分析的算法进行求解。

图2 车身安装点的约束情况

分析模型搭建通常分为3 个步骤，建立局部坐标系、创建载荷及接触。

（1）进入编辑模块，选择压头所在的comp，坐标 Node_id 选择一个刚体参考点来控制整个刚体。检查整个模型中的全部属性，是否缺失材料属性等。若缺失材料或属性，重复上述步骤新建或更新相应部分。

由于压头需要约束其除法向以外的其他自由度，所以需要建立局部坐标系。将压头上的参考点都放入到局部坐标系中，同样在systems 中将其assign 到局部坐标系中。

（2）创建约束载荷集，保存对翼子板的约束。选择要建立约束的点，以及约束的方向。翼子板抗凹分析，车身安装点处约束全部自由度1、2、3、4、5、6，压头处约束1、2、4、5、6（由于是往Z 向施加力，所以释放3 个方向自由度）。将其都放在一个载荷集中，也可以分别建立相应的载荷集。进一步创建力的载荷集，保存对翼子板施加的力，此处的力为400 N。

（3）在接触中需要创建接触面，接触对以及接触属性。通常情况下，选择两物体中硬度较大的一方为接触体，其接触表面称为接触面。主面选择刚性压头，从面选择翼子板。创建分析步加载力和卸载力[3]。

3 计算结果

在翼子板上选择合适的点来进行分析，通常考虑关键点即材料或结构中承受压力最大的关键点、均匀分布、代表性及可重复性等综合因素。经过分析研判，选取23 个参考点（图3）。考察其抗凹性能，其计算结果统计如表1 所示。

图3 参考点位置

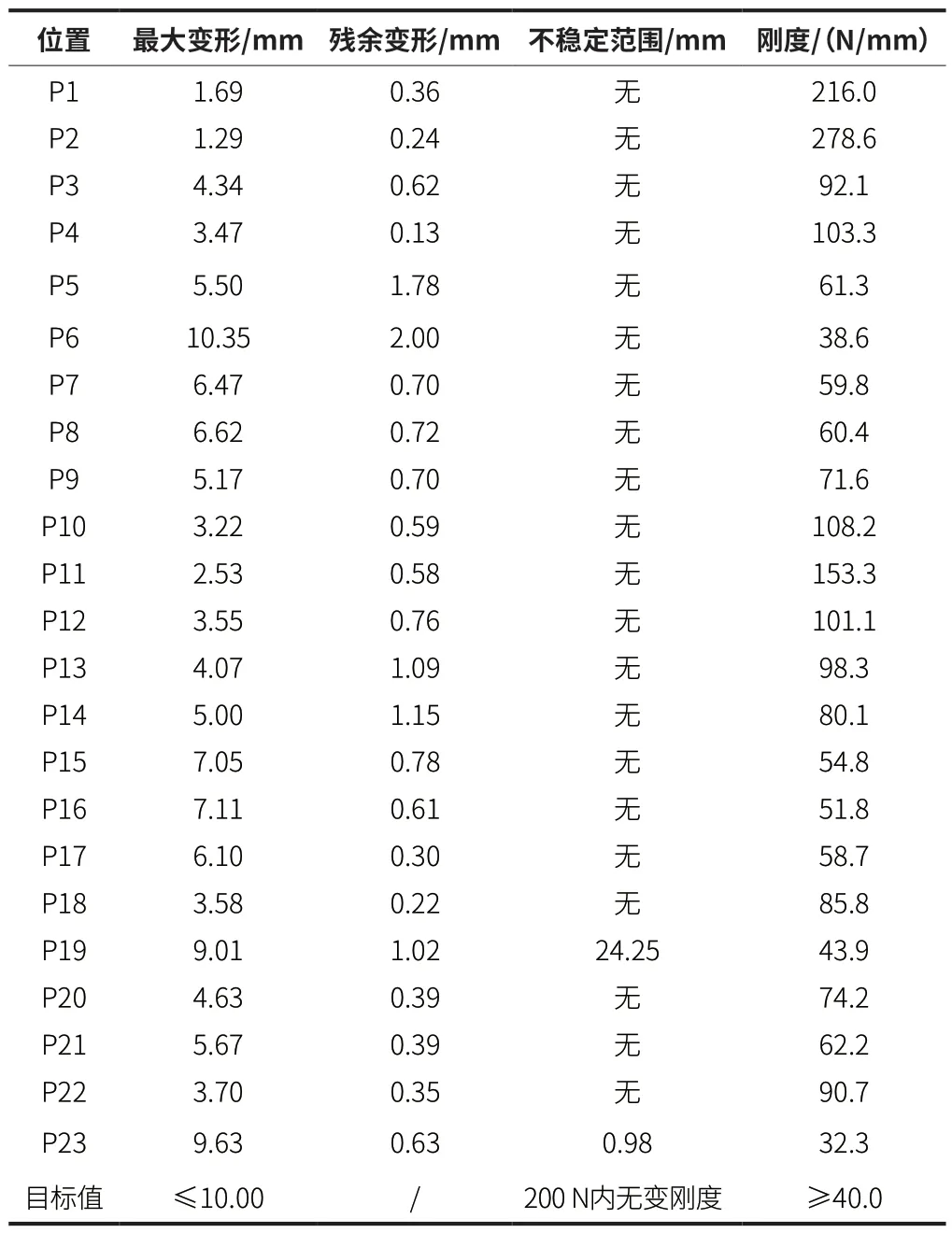
表1 各考察点的计算结果

23 个考察点的载荷曲线位移图分别如图4 ～图6 所 示。由计算结果可知，点P6、P19 和P23 在400 N 力的作用下发生了显著的屈曲变形，因此点P6、P19 和P23 不满足抗凹要求。

图4 载荷-位移曲线图（P1 ～P10）

图5 载荷-位移曲线图（P11 ～P20）

图6 载荷-位移曲线图（P21 ～P23）

结果分析表明，该翼子板抗凹性能较弱，即材料或结构在承受外部压力时容易发生凹陷或变形的现象，可能会导致材料或结构的失效或破坏，因此需要进行相应的局部优化。在汽车设计时，可以采用更加坚固的支撑结构，如增加支撑板或增加胶等，以提高其抗凹性能，改善该处的局部抗凹性。

在汽车结构设计中增加支撑板是一种常见的增强结构强度的方法。支撑板可以通过增加结构的厚度、改变材料的种类以及改变结构的形状等方式来提高结构的强度和稳定性。通过增加加强板的厚度，通常适用于需要承受较大荷载的部位，如车门、发动机舱盖等外板处；使用更加坚固的材料来制作加强板，通常适用于需要承受较大冲击或振动的部位，如底盘、悬架等；改变加强板的形状，通常适用于需要承受复杂荷载的部位，如车身框架、底盘等。

在优化方案考虑时，需要考虑到结构的整体性和平衡性，以避免因局部加强而导致其他部位的薄弱。支撑板的设计和安装也要符合相关的标准和规范，以确保其有效性和安全性[4]。

4 优化方案

有限元优化是一种通过调整有限元模型的参数来优化结构性能的方法。通常有6 种有限元优化方案，分别为尺寸优化、形状优化、拓扑优化、材料优化、多目标优化及智能优化算法等[5]。优化时需要从成本及工艺实施性综合考虑，找出投入与产出平衡的方案。下面介绍本案例所采用的优化方法。

在不合格点处增加胶片，胶片选取厚度为1.50 mm，建立增加胶片后的有限元模型（图7）。需要注意的是，增加胶片虽然可以提高结构的承载能力，但也可能会增加结构的质量和成本，因此需要综合考虑结构的实际需求和经济效益，选择最优的方案。同时，也可能会产生新的应力集中点，需要根据分析结果进行进一步的优化。

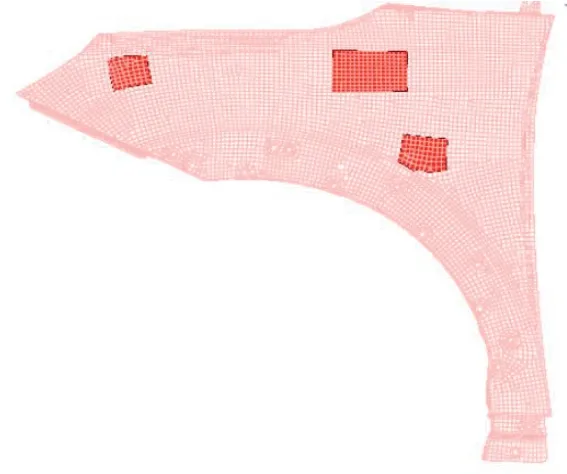
图7 增加胶片位置

对增加胶片后的模型施加相应荷载并进行分析，得到该区域的应力和变形情况，分析结果如表2 所示。

表2 不合格点的优化计算结果

不合格点的载荷曲线位移图如图8 所示。通过分析比对初始数据发现，点P6、P19 和P23 的形变量及刚度都满足目标值。

图8 改进后的载荷-位移曲线图（P6、P19 和P23）

5 结束语

在实际的设计与生产中，影响翼子板屈曲抗凹性能的原因有很多种，如材料、工艺、温度及试验条件等。要提高翼子板的屈曲抗凹性能，需要综合考虑综合因素，并采取相应的措施，配合优化设计，达到翼子板的强度性能。

本文利用CAE 软件对某车的翼子板进行屈曲抗凹分析，存在薄弱位置。根据分析结果对翼子板抗凹性做出了评价，并提供了局部优化方案。经过检测后证明，优化改进后的翼子板抗凹性能得到了明显改善，屈曲抗凹分析对翼子板等外板结构的优化提供了理论依据。