核电站燃料水池清洗机器人框架拓扑优化设计
2024-01-11段洪斌吴东栋
段洪斌,张 斌,王 希,吴东栋
(核动力运行研究所,湖北武汉 430223)
0 引言
核电站燃料水池经过长时间运行,池底和池壁会附着放射性腐蚀活化产物,需要人工定期进行清洁去污。现有清洁去污过程为,先将池水排空,然后采用泡沫去污[1]或者高压水射流去污[2-3]的方式,人工携带喷枪将附着在池壁和池底的松散污染物去除。清洁去污过程中,人员受照剂量大、劳动强度高。
核电站燃料水池水下清洗机器人可以在不排空池水的前提下,自动对池壁进行清洁去污。该设备可以降低人工清洁时的人员受照剂量和劳动强度,因此在核电水池清洁领域有广阔的应用前景。
水下清洗机器人整体质量越大,则所需浮块越多,整体尺寸也越大。此外,在核电站燃料水池有限空间内,机器人质量和尺寸大,其运动灵活性、操作便利性都会大大降低。因此,在总体结构设计确定的前提下,对水下机器人进行轻量化设计是非常必要的[4]。框架作为机器人的主要承力部件,质量占比高,优化空间大。
结构优化设计分为尺寸优化、形状优化和拓扑优化3 个层次。拓扑优化可以通过在设计域空间中寻求最佳传力路线,在指定区域内对材料分布进行优化,使材料发挥最大利用率,从而减轻结构的重量。尤其在设计初始阶段,初始结构拓扑未知的情况下,通过拓扑优化可以获得结构最优的拓扑结构,用于后续设计的参考[5]。拓扑优化常用的方法有均匀化法、变密度法、渐进结构优化方法、独立连续映射模型法、水平集方法等,其中变密度法是最具代表性的方法之一,具有程序实现简单、计算效率高等优点[6-7]。ANSYS Workbench 软件中Topology Optimization 模块可采用变密度法进行拓扑优化,在众多领域中得到应用[7-10]。
本文以自主设计的核电站燃料水池清洗机器人为研究对象,利用ANSYS Workbench 有限元分析软件实现对机器人框架的轻量化结构设计。针对机器人板式框架结构,建立合理的有限元分析模型,利用Topology Optimization 模块对框架进行拓扑优化分析并重构模型,将优化前、后的框架进行静力学分析并对结果进行对比,使得框架质量大大降低。
1 机器人和框架简介
1.1 机器人结构
机器人总体尺寸930 mm×600 mm×350 mm,总质量约60 kg,由一个浮游模块、两个爬行模块、两个清洗模块组成,前后左右方向对称布置(图1)。其中,浮游模块实现水下空间的自由运动、姿态调整定位和功能检测;爬行模块实现机器人爬壁清洗作业时的直行和转弯等功能,为壁面清洗提供稳定的作业环境;清洗模块实现对水池壁面污物的清洁去污。

图1 水下清洗机器人
1.2 机器人框架
机器人框架是其他各个模块的安装基础,是主要承力部件,其质量具有较大的优化空间(图2)。在总体设计尺寸确定的前提下,机器人框架轻量化设计可以从材料选择和结构拓扑优化入手。水下机器人框架常用材料有不锈钢、铝合金、钛合金、聚丙烯等[11],其中铝合金具有较高的比强度和比刚度,综合性能优异,也能够满足核电燃料水池环境。

图2 原始框架三维模型
原始框架整体质量34.3 kg,采用6061-T6 铝合金材料。材料的弹性模量69 GPa,泊松比0.33,密度2713 kg/m3,屈服强度240 MPa。
1.3 机器人框架受力分析
机器人框架在水下工作过程中主要受到4 个垂向推进器、4个水平推进器、履带模块、清洗模块、电子舱、浮体、电缆等零部件反作用力;在吊装过程中,承受吊装冲击载荷(表1)。

表1 不同工况下框架的受力情况
2 原始框架静力学分析
2.1 有限元模型建立
运用ANSYS Workbench 有限元分析软件进行静力学强度分析。根据框架结构和受力对称性特点,取1/4 模型作为研究对象并采用壳单元建模(图3)。相对于实体单元和全模型建模,采用1/4 壳单元模型能够大大减少网格数量并提高网格质量,采用壳模型拓扑优化结果更符合板材加工工艺,采用1/4 模型拓扑优化结果便于获得预期的对称框架模型。
图3 原始框架分析模型
2.2 网格划分和边界条件
为提高拓扑优化轮廓的光滑性,采用较小的网格尺寸,设置全局单元大小3 mm。
框架各个板之间通过螺栓进行连接,将其作为一个整体进行分析能大大降低计算量和复杂度,且不会影响整体结果[12]。设置对称面,约束爬行模块安装孔Y 向位移为0。将表1 中水下工作过程和吊装过程时的受力进行组合,并考虑一定的安全系数,同时在模型上施加载荷(图4)。其中推进器根据其推力作用点施加为远程载荷,部分载荷大小根据1/4 模型特性做相应变化。

图4 分析模型载荷情况
2.3 分析结果
在ANSYS Workbench 种进行静力学求解计算,得到原始框架的强度分析结果(图5)。从图5 可以看出,框架大量结构材料所受应力较低,未能充分发挥材料性能,具有较大的优化空间;最大应力17.3 MPa,远小于屈服强度240 MPa,最大变形0.25 mm,满足工作要求。
3 框架拓扑优化与分析
3.1 拓扑优化
将原始框架静力学强度分析结果导入Topology Optimization模块,各边界条件保持不变。根据使用要求,设定框架外围轮廓及各施力点为不可去除材料区域,以去除材料88%材料为优化目标进行求解,计算后得到拓扑优化模型如图6 所示。

图6 拓扑优化分析云图
3.2 模型重构
拓扑分析后的模型可以通过重构几何模型和刻面片直接光顺化两种技术处理,直接用于实际产品仿真设计验证和制造使用。重构几何模型即结合设计经验对整体结构重新设计,加工工艺更容易控制,有限元验证计算过程中网格划分和加载等控制更简单。而拓扑直接光顺化几何设计一般通过增材制造实现,难以直接加工,也难以再次进行设计变更。因此,采用重构几何模型的方法对拓扑分析模型进行优化。
在ANSYS Spaceclaim 中对拓扑分析模型进行重构。根据拓扑结果,同时考虑加工工艺,重构优化框架三维模型如图7,整体质量8.9 kg。

图7 优化框架三维模型
3.3 优化框架静力学分析
对优化后的框架模型进行静力学强度分析,材料、载荷、约束等边界条件与原始框架静力学分析完全一致。求解计算结果如图8 所示。从图中可以看出,框架结构材料得到较为充分的利用。最大应力23.7 MPa,远小于屈服强度240 MPa,最大变形0.60 mm,满足工作要求。
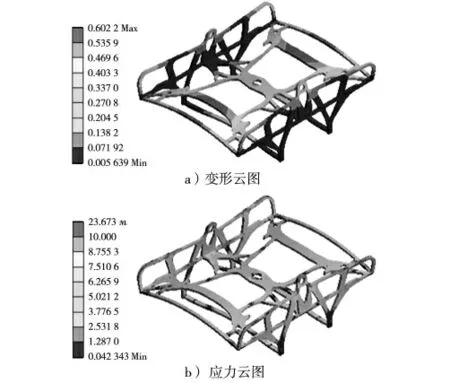
图8 优化框架静力学分析云图
3.4 优化前后结果对比
对清洗机器人框架进行拓扑优化,对优化前后的模型进行静力学分析,性能参数对见表2。优化前后,框架的应力和应变均满足材料性能要求和工作要求,优化后框架的质量为8.9 kg、比优化前减少74%。

表2 拓扑优化前后框架的数据对比
4 结论
本文以核电站燃料水池清洗机器人的框架为研究对象,采用拓扑优化的方法对其进行轻量化设计。得到如下两个结论:
(1)根据框架结构特点和对称特性,取1/4 框架并采用壳单元作为有限元分析对象。拓扑优化并模型重构,获得优化后框架结构。优化后框架质量为8.9 kg,比优化前的34.3 kg 减少74%,应力和应变均满足工作要求。
(2)拓扑优化方法大大降低了水下机器人框架重量,可以为开架式机器人和其他板类框架结构优化设计提供参考。
