不同线性拟合方法对直剪试验结果影响的分析

罗 杰，贾 静

（河北省水利水电勘测设计研究院集团有限公司，天津 300220）

目前，在岩土工程项目检测试验中，尽管现行规程规范条文大力提倡通过三轴压缩试验获得土的抗剪强度指标，但由于直接剪切试验（以下简称为直剪试验）的方法简单、高效和大量经验积累，其仍是目前岩土工程中获得抗剪强度指标的重要手段。

在直剪试验数据处理方法上，土工试验规程［1-2］或土工试验方法标准［3］中均未指定试验数据线性关系式的拟合方法， 只在数据处理部分的条文中规定采用图解法［1-3］确定试样的抗剪强度指标。但随着计算机的广泛应用，越来越多的数据处理通过计算机来完成。 本文通过实际工程项目的直剪试验数据为例， 分别采用最小二乘法、梯度降减法拟合试验数据的线性关系式，根据各自关系式确定抗剪强度指标C，φ 值。同时,以实际试验数据为标准, 分析采用不同方法拟合的线性关系式可靠性； 以最小二乘法确定的抗剪强度指标为参照值， 比较其他方法确定抗剪强度指标与其之间的差异。

1 试样基本物理性质指标

试样的基本物理性质指标如表1。

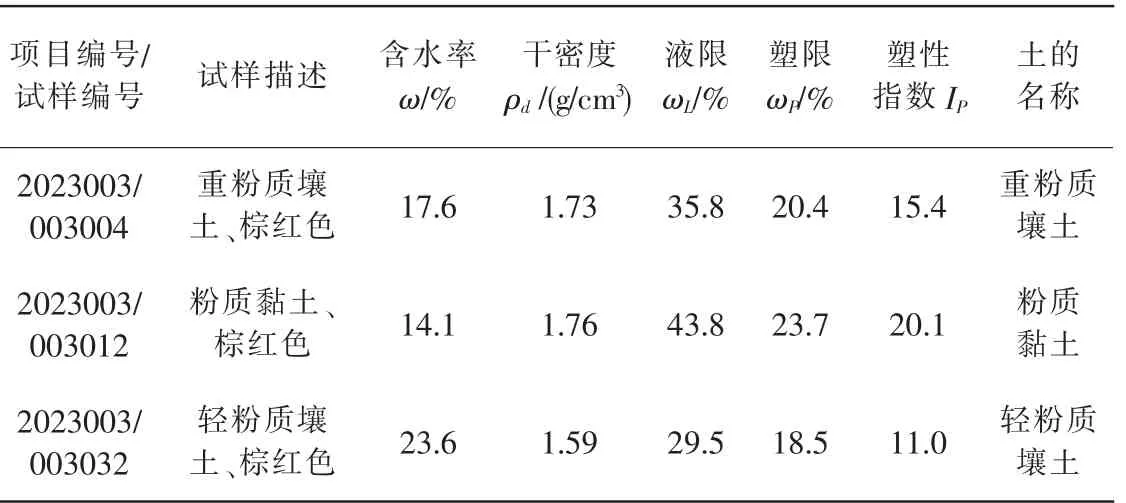
表1 试样基本物理性质指标

从表1 试样的基本物理性质指标可看出：3 个试样均属黏性土。

2 直剪试验数据

为更好地比较分析不同线性拟合方法对直剪试验数据拟合结果的影响， 在实际工程工程项目的土工试验中，选取离散性差别较大的3 组试验数据，如表2。

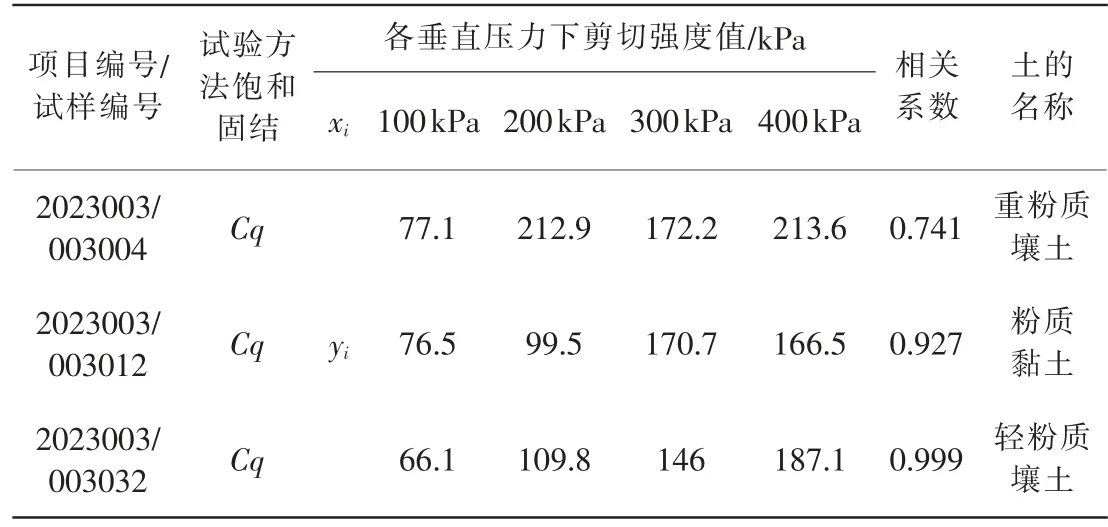
表2 直剪切试验数据

从表2 可知：在3 组数据中，第1 组数据的离散性最大，第2 组数据的离散性次之，第3 组数据的离散性最小。

3 最小二乘法［4-5］

为确定试样的抗剪强度指标（C，φ），需根据不同垂直压力下的抗剪强度绘制关系曲线或拟合关系式，一般情况下关系曲线为直线，关系式为线性表达式。 通过线性关系式中的参数达到确定试样抗剪强度指标（C，φ）的目的。目前，为提高工作效率和保证成果质量， 基本采用办公软件或专业软件进行数据处理。

由于最小二乘法简便， 是实际工作中较常用的线性关系式拟合方法。最小二乘法基本原理：采用偏差平方和最小的原则拟合线性关系式。如设：线性表达式的型式为y=a+bx，针对表2 数据，其矩阵方程组为：

解方程组得：

依据上述两式和表2 数据,分别计算各试样试验数据拟合的现行表达式参数a，b 值。计算过程及计算结果如表3。各试样的抗剪强度与垂直压力关系曲线如图1。

图1 抗剪强度与垂直压力的关系曲线

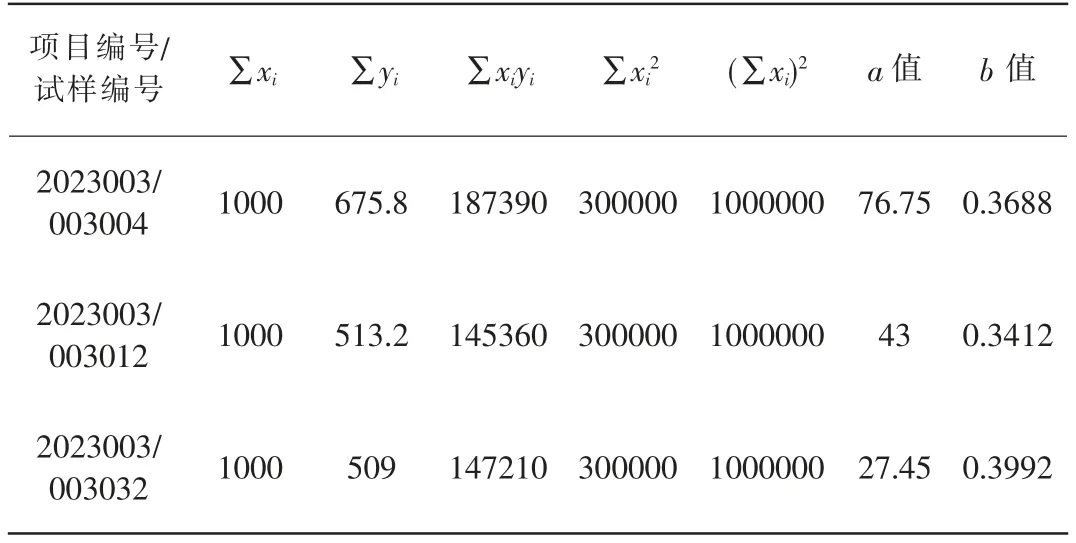
表3 各试样试验数据拟合的现行表达式参数计算结果

从图1 可看到：所显示公式中的a，b 值与表3 中的计算值完全一致，因此，借助Excel 选取散点图，其数据的线性趋势线拟合方法采用的是最小二乘法。

4 梯度降减法［4,6］

梯度降减法需进行迭代计算，有时还需进行优化后才能确定最后结果，因此在电算化没有广泛普及的年代，其使用受到一定限制。但今天，广泛普及的计算机应用已完全化解此问题。

本文应用梯度降减法的基本思路：在坐标图中，沿着代价函数在某点处切线的降低方向， 通过各待求变量变化的适当步长，确定代价函数的下一点，并对应1 个预测函数。 然后以此点处代价函数切线的降低方向，通过相同的变量变化步长，确定代价函数的另一个下降点，同样对应1 个预测函数。如此不断地找下去，直至找到满足要求的代价函数最小值或约定的变化值所对应的点，此时对应的预测函数是所需的最终结果。

设拟合的线性表达式（预测函数）为：y=a+bx

为评判获得的预测函数是否满足要求，引入均方差代价函数。

设均方差代价函数（或称平方差代价函数、损失函数）为：

式中 m 为数据组数（样本数），本文实例中m=4；1/2 为常量， 为在求梯度时能把二次方乘数加以抵消，这样方便计算且不会影响计算结果；yi为试验实测数据值；ya，b为预测函数。根据a，b 值得到预测的y值。即：ya,b(xi)=a+bxiaj，bj值的迭代计算公式如式（8）～式（9）：

根据表2 中试样编号为003004 的试验数据，采用梯度降减法进行迭代计算的过程及计算结果如表4。 通过优化， 在计算过程中aj，bj的初始值选取为：a0=20，b0=0.4；步长值选取为：αa=0.3，αb=0.00002。

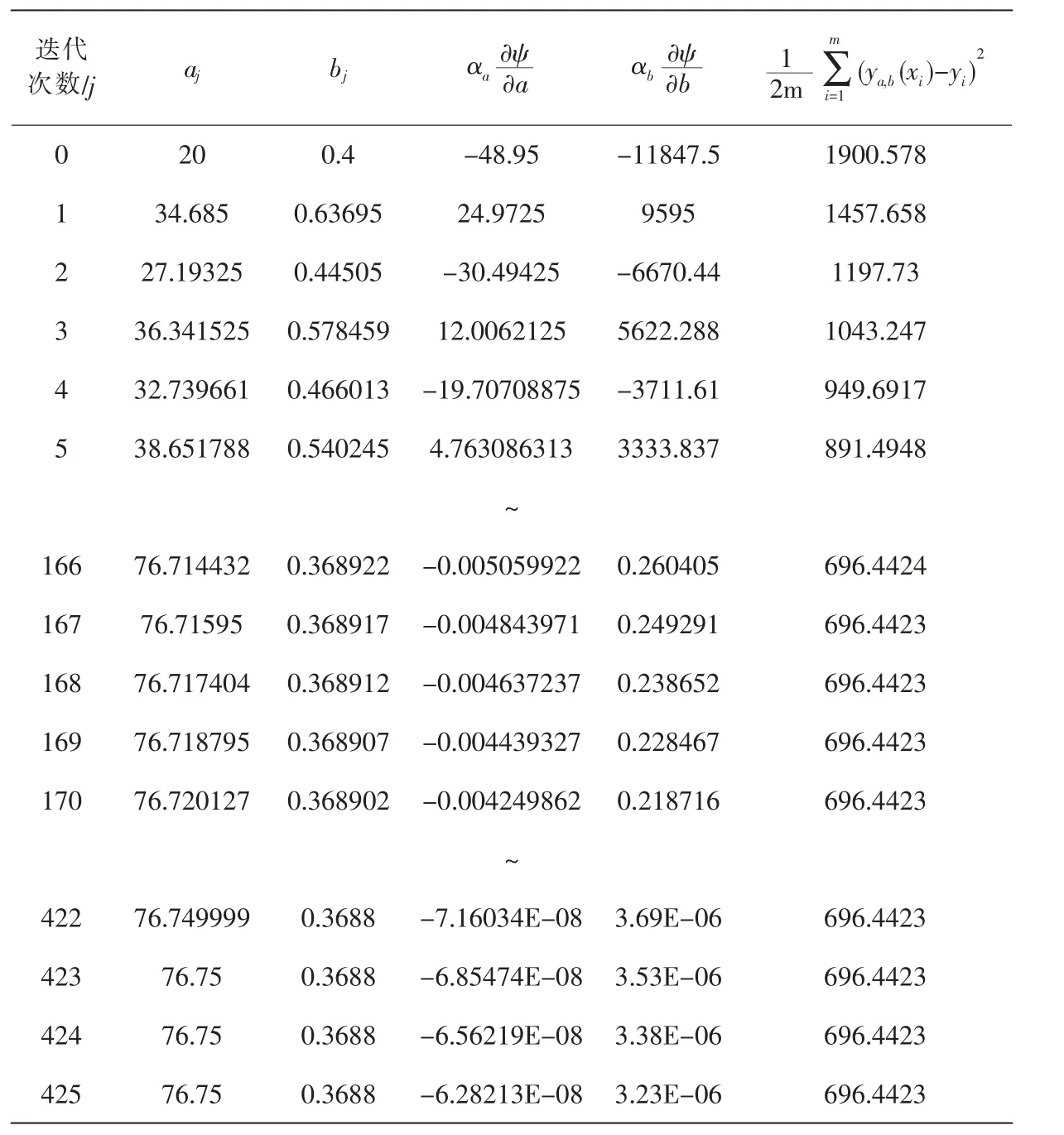
表4 直剪试验数据线性拟合表达式参数a，b 值迭代计算

从表4 中aj，bj的迭代计算过程和计算结果可看出： 当以均方差代价函数的最小值或约定的变化值为判断标准时，a=76.717404，b=0.368912，修约后，a=76.72，b=0.3689。 预 测 函 数 的 最 终 关 系 式 为：y=0.3689x+76.72。 与上述采用最小二乘法获得的关系式非常接近。同时，从表4 还可看出：如果持续增加计算步骤， 那么最终的a，b 值与采用最小二乘法获得的值完全相同。

同理，根据表2 中试样编号为003012 的试验数据， 通过优化， 在计算过程中aj，bj的初始值a0=20，b0=0.4。步长αa=0.3，αb=0.00002。当以均方差代价函数的最小值为判断标准时，a=42.9775，b=0.341277，修约后，a=42.98，b=0.3413。 预测函数的最终关系式为：y=0.3413x+42.98。

同理，根据表2 中试样编号为003032 的试验数据， 通过优化， 在计算过程中aj，bj的初始值a0=20，b0=0.4。步长αa=0.3，αbt=0.00002。当以均方差代价函数的最小值为判断标准时，a =27.447728，b =0.399208，修约后，a=27.44，b=0.3992。预测函数的最终关系式为：y=0.3992x+27.44。

5 关系式可靠性分析

为验证上述关系式的可靠性， 以试验实测数据为基准值， 比较采用各方法拟合关系式的计算值与基准值的偏差情况，如表5、表6。从表5、表6 可看出： 采用不同方法拟合的线性关系式并分别计算在不同垂直压力下的抗剪强度，计算结果略有不同，相差不大，但与实测数据均存在一定偏差，其偏差绝对值随各组试验数据离散性增大而增大。

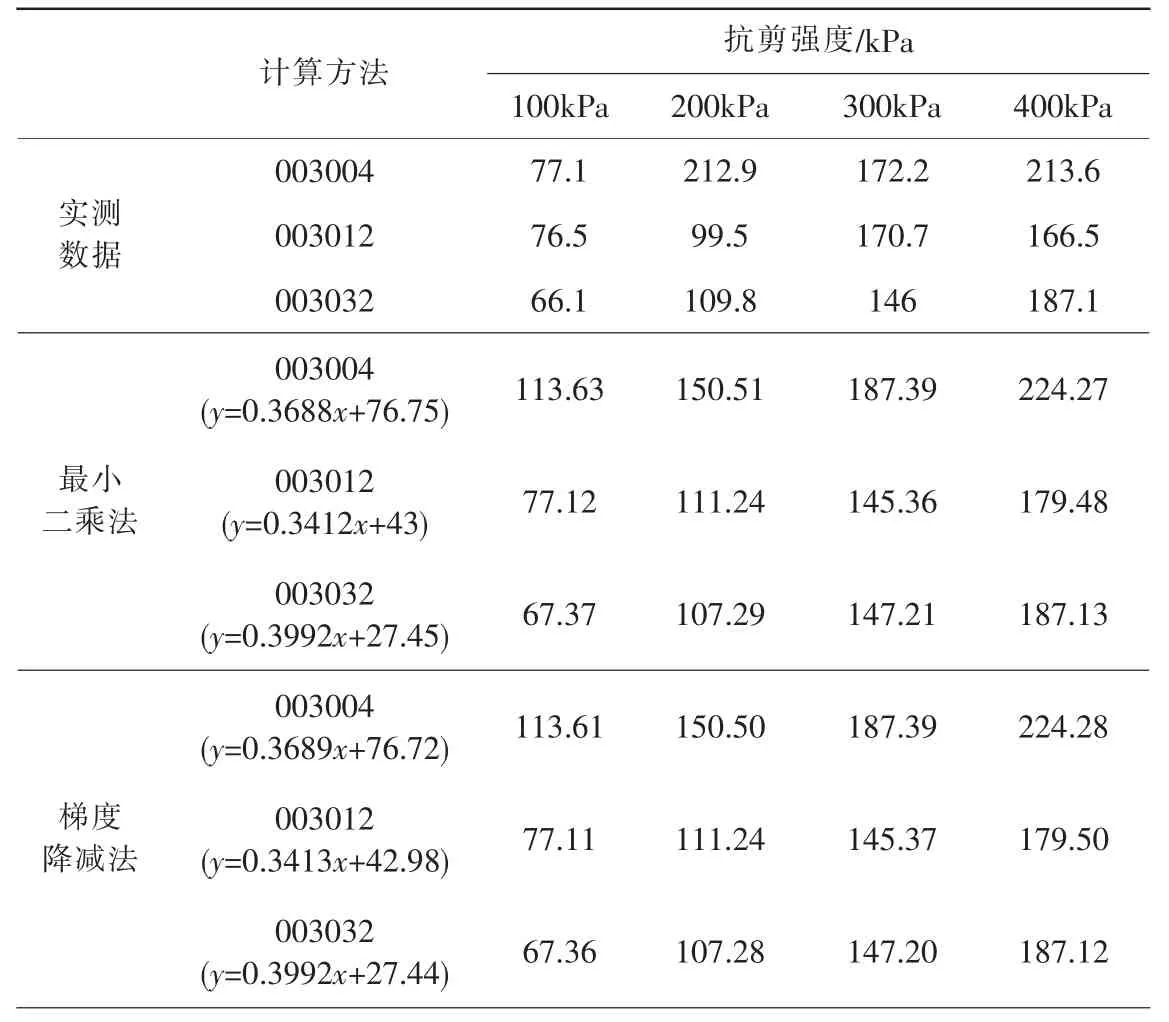
表5 各垂直压力下抗剪强度的实测值和关系式计算值

表6 采用不同计算方法线性拟合关系式计算的抗剪强度与实测值偏差情况

6 不同方法确定抗剪强度指标的差异

最小二乘法：为方便求解，需关心误差函数在迭代值处的局部性质， 而不用考虑在迭代值处的全局性质，这种方法机器学习领域使用的非常广泛。

梯度降减法： 是用于找到可微函数的局部最小值的一阶迭代优化算法。 为了使用梯度下降找到函数的局部最小值，采取与该数在当前点的梯度（或近似梯度）的负值成比例的步骤。梯度下降法每次都以梯度的反方向下降，所以，有可能会走出锯齿路线，从而增加迭代次数。

不论什么方法，只要选好初始参数，就可减少迭代次数，从而减少计算量。在实际使用中，可根据具体情况决定用哪种方法优化求解。

不同线性拟合方法确定的试样抗剪强度指标如表7。

表7 不同线性方法确定的抗剪强度指标

从表7 可看出： 两种方法确定的抗剪强度指标几乎没有差别。

7 结语

（1） 对直剪试验数据线性的拟合方法不是单一的。 拟合方法不同， 其结果也可能不同。为了保证数据的连续性，尽可能采用同一种线性拟合方法。

（2） 在两种线性拟合方法中，最小二乘法最简单、最方便。一组试验数据采用某种方法拟合线性关系式后，要验证关系式的可靠性，当发现综合误差较大且不满足实际要求时，应考虑采用其他线性拟合方法。