插入型组合式金属防洪挡板有限元仿真分析
2024-01-11秦英泉吕中荣徐丹丽刘祚秋
秦英泉,邓 飞,吕中荣,徐丹丽,刘祚秋
(1.中山大学 航空航天学院,广东 深圳 510006;2.广东水利水电技术中心,广东 510635)
组合式金属防洪挡板结构稳定安全可靠, 可应用于小型住户、城市街道,也可用于堤坝加高,提高堤坝原有的防洪强度, 因此组合式金属防洪挡板的应用研究逐渐成为热点。 组合式金属防洪墙由以下部分组成[2]:立柱、挡板、预埋件、锁定装置、水封,在不同工况下还会加入加强件。 一般的组合式金属防洪挡板通常在预埋件部分采用螺栓连接, 本文提出一种插入式的组合式金属防洪挡板, 其预埋件部分仅为一个与立柱尺寸相同的钢材插槽, 通过改变插入深度来加强立柱底部的约束力。 插槽的四周带有止水橡胶, 一方面防止水流渗入底座影响底部约束力,另一方面止水橡胶作为弹性材料,还能起到减震效果。 这种结构在实地安装过程中可减少螺栓安装时间,直接将立柱插入插槽中,节约时间的同时,达到较好的防洪效果。对于插入型的防洪挡板,插入深度越大,底部对立柱的约束力也越大,防洪效果自然也越好,但并不是越深越好,越深意味着同样挡水高度的情况下,立柱的长度需求越大,所需要的材料也越多,不符合经济要求,为选取更符合防洪要求与经济要求的防洪系统, 需分析不同高度的立柱与插入深度的关系。
组合式金属防洪挡板是一种较为复杂的结构,对于其力学性能的分析可使用实验的方法进行分析[1-2],但对一个生产周期长、 生产成本高的大型装配体直接进行实验显然不适合。 而使用理论计算的方法也很难获得准确的解析解[3],因此可使用有限单元法将结构离散成有限个单元进行分析以获取其数值解[4-5]。本文使用ABAQUS 软件,对插入式防洪挡板立柱装配体进行多种工况的有限元分析, 分析插入式组合式防洪挡板的应力和变形情况, 为插入型组合式金属防洪挡板的使用提供参考。
1 建立有限元模型
1.1 模型的建立
通过对草图进行一系列拉伸、切削操作,对各个部件进行建模,包括土壤、混凝土底座,钢板部件,橡胶,双向立柱,将钢板容器插入混凝土,再将4 块橡胶贴上钢板4 个面上,再将立柱插入钢板容器中,最后将结构插入土壤中,引入导角以避免应力集中。立柱高度分为1、2、3 m, 插入深度为0.2、0.3、0.4 m,混凝土厚度均在插入深度的基础上往下延伸0.2 m。为了准确设置接触面与受力面, 根据挡水面高度与插入深度对立柱与挡板进行面分割操作,最后得到如图1、图2 结构。挡板的上部呈凸状,下部则呈凹状,通过上下表面的凹凸结构相互齿合,提高结构稳定性。

图1 单跨长度3 m 防洪挡板

图2 挡水高度3 m、插入深度0.4 m 装配体结构
1.2 ABAQUS 有限元仿真前处理
由于ABAQUS 中没有单位标注,在仿真过程中要保证前后单位一致,对力学结构进行简化建模后,以实体单元导入ABAQUS 中。给各个部件设置材料参数,材料参数对仿真结果产生重要影响,贴近实际的材料参数也能使仿真结果更准确, 表1 列出结构各项材料参数,其中包括杨氏模量、泊松比及密度等参数。该型结构的止水条一般由止水橡胶组成,止水橡胶的重量与其他部件相比可忽略不计, 因此在计算中可不考虑橡胶的重量。
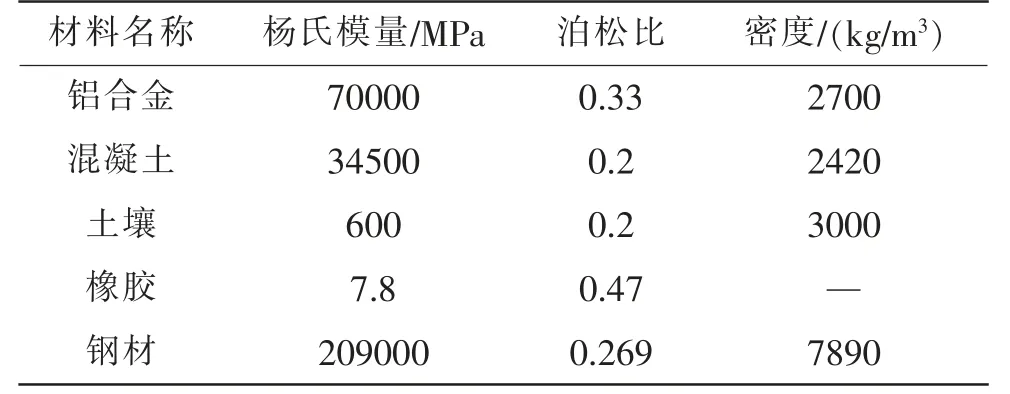
表1 材料参数
接触设置中,将橡胶与钢板、钢板与混凝土、混凝土与土壤的接触设置为绑定约束, 即将整个底座看作一个固定整体,其余接触设置:切向摩擦公式为罚函数,摩擦系数为0.5;法向压力过盈为“硬”接触,约束执行方法为标准罚函数(罚(Standard))。
对于有限元分析, 正确的网格划分能有效提高计算的精准度,所谓正确的网格,并不是指网格越细越好,细网格虽然会带来更精确的结果,但同时也会耗费更多的计算资源,更长的计算时间。在满足工程实际要求的同时, 综合考虑计算机的算力限制与运算成本, 给不同的部件采用不同的网格类型与网格尺寸,得到如图3 网格结构:土壤、混凝土、钢板、加强件均使用四面体网格,几何阶次为二次;橡胶网格为六面体,几何阶次为二次并使用杂交公式;立柱使用六面体网格。

图3 挡水高度3 m、插入深度0.4 m组合式防洪挡板网格
2 有限元仿真结果
本次模拟挡水高度为1、2、3 m,插入深度为0.2、0.3、0.4 m,单跨长度均为3 m 的两跨装配体结构,下面给出两跨装配体在受静水荷载、 动水荷载及漂浮物冲击荷载3 种荷载共同作用下的应力与位移的有限元仿真结果,假定流水速度为3 m/s,水流与装配体结构的最大夹角为30°,水密度为1000 kg/m3,漂浮物最大质量为400 kg。 冲击荷载作用于双向立柱自由水面高度的两边。
挡水高度为3 m, 插入深度为0.4 m 及0.3 m 的仿真结果如图4~图7,其中变形图放大20 倍,显示背水面的应力分布。

图4 挡水高度3 m、插入深度0.4 m 组合式防洪挡板应力云图
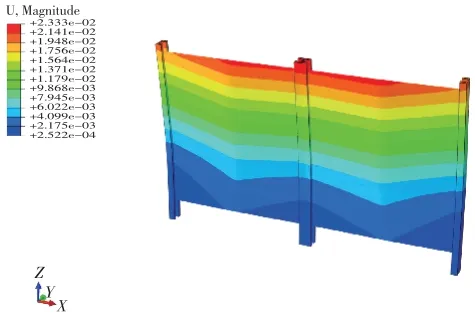
图5 挡水高度3 m、插入深度0.4 m 组合式防洪挡板位移云图
图4、图6 所示立柱的应力总体呈从上往下递增趋势,但立柱的最大应力出现在变截面处,即与加强件连接的两处地方; 挡板的最大应力出现在挡板的中部且越底部的挡板应力越大。对于单跨3m、插入深度0.4m、挡水高度为3m 的结构,立柱与挡板的最大应力为75.22 MPa,小于材料容许应力160 MPa。而对于插入深度为0.3 m 的结构,其最大应力为215.4 MPa,超过材料容许应力160 MPa, 该插入深度不足以完全支撑立柱,所以在本次模拟的立柱、挡板与加强件的型号与结构中,在挡水高度为3 m 的情况下,立柱的插入深度不宜小于0.3 m。

图6 挡水高度3 m、插入深度0.3 m 组合式防洪挡板应力云图
图5、图7 所示结构的变形量,由于两侧立柱结构不一样,其变形与中间双向立柱相比不同,因此挡板的变形情况并不对称, 单块挡板的最大变形量出现在挡板中部,且越往下挡板位移越小;上部的挡板虽然受力比底部小, 但立柱上端的位移比下部的位移更明显,立柱带动挡板位移,因此顶部挡板的位移也会逐渐增大, 而挡板底部由于受到最大的静水荷载,因此其位移大于中间的挡板。插入深度为0.4 m时立柱最大位移为2.333 cm,对于跨度3 m、挡水高度3 m 的结构而言,在应力满足容许应力的条件下,该变形属于小变形, 能够满足结构的安全与稳定性要求。

图7 挡水高度3 m、插入深度0.3 m 组合式防洪挡板位移云图
对于复杂的水情, 不同的挡水高度使用同样的插入深度或较低的挡水高度使用较深的插入深度显然不符合经济效益, 为满足防洪要求同时兼顾经济效益, 对于同一插入深度的结构需对不同挡水高度进行分析, 给出不同挡水高度与插入深度的仿真结果, 如表2, 给出挡板与立柱的最大应力与最大挠度, 其中1m 挡水高度的结构仅承受动水与静水荷载,且无加强件支撑。

表2 不同挡水高度与插入深度的防洪系统的最大应力及最大挠度
在表2 的仿真工况中, 根据3 m 的仿真结果可看出,在防洪墙的挡水高度大于2 m 小于3 m 时,对于当前材料与结构型号,插入深度选取0.4 m 会在满足防洪强度的情况下更符合经济效益; 根据2 m 的仿真结果可看出,在当前加强件的型号下,对于2 m结构, 其插入深度对应力的影响比加强件对应力的影响要小, 当前加强件的型号足以支撑2 m 的洪水高度。而从对挡水高度为1 m,插入深度0.2 m 结构的分析结果来看, 在无冲击荷载情况下其最大应力166.9 MPa 已超过材料的容许应力,因此对于该型插入型防洪挡板,对大于等于1 m 的防洪高度而言,其插入深度都不应小于0.2 m。
3 结语
(1) 对插入型组合式金属防洪挡板系统建立有限元模型,利用ABAQUS 有限元仿真软件,对结构力学性能进行仿真计算,结果表明,该型组合式防洪挡板系统可将结构承受的组合载荷通过挡板传递到立柱,立柱通过插入混凝土固定于地面,达到挡水效果,结构较为合理,无应力集中情况。
(2)从图4、图6 可看出,立柱最大挠度均出现在立柱顶部,且从上至下逐渐减小,说明加强件的存在使得立柱在承受底部更大水压的情况下能有更小位移, 证明底部加强件能起到加强立柱支撑能力的作用。
(3) 防洪挡板的挡水高度大于2 m 小于3 m,受静水、动水及冲击3 种组合荷载时,插入深度选取为0.4 m 时的最大应力与最大挠度均满足当前材料的使用要求, 在使用安全的范围内。 而当插入深度为0.2 m 时, 结构最大应力均超过材料的容许应力,因此对于该型插入型防洪挡板, 对大于等于1 m 的防洪高度而言,其插入深度都不应小于0.2 m。
