防弹用经编轴向织物的三维仿真
2024-01-11蒋高明杨美玲李炳贤
王 婷,蒋高明,杨美玲,李炳贤
(江南大学 针织技术教育部工程研究中心,江苏 无锡 214122)
随着现代战争中防弹武器的更新以及适应士兵在战场上生存能力的需求,防弹材料需要具有更高的舒适性、保护性和灵活性。在确保身体护甲原始防护性能的基础上,轻巧、柔软成为防弹材料选择的基础。使用高性能纤维通过纺织技术制成的防弹材料属于软质材料,采用纺织技术开发的防弹用纺织品材料国内外已有研究[1-3],但大部分以机织和非织造布为主,以经编制成的防弹织物研究较少。
经编轴向织物具有优良的力学性能,每行衬入纱线笔直且平行,只有捆绑纱存在微量屈曲,外力击中后平行伸直的纱线可以同时承受载荷[4],所以纱线不容易产生断裂,适用于防弹领域。金利民[5]针对双轴向经编针织复合材料建立细观结构模型,结合有限元分析了复合材料的弹道侵彻性能。竺铝涛[6]研究双轴向多层经编针织复合材料中纤维的应变率效应并使用单胞尺度计算出弹道防护能力。
基于这种特点,本文介绍了一种特殊的防弹用经编轴向织物,该织物由地组织和衬纬纱同向垫纱形成闪避垫纱,使得衬纬纱在受到纱线张力及延展线的作用后呈现伸直状态,形成衬经的纹理效果与全幅衬纬呈90°衬入织物,形成类似机织物一样的纹理效果。通过衬纬纱满穿配置,闪避垫纱效应增加织物的经纱横密,利用轴向织物内部应力较小,仅捆绑纱处存在轻微屈曲,提高织物防弹效果。在分析该防弹用经编轴向织物的编织和结构特点的基础上,采用JavaScript和C#作为计算机程序设计语言进行计算机编程,分别建立了织物的垫纱模型、穿经模型和线圈模型,通过分析闪避垫纱位置和衬纬受力情况,实现织物的三维仿真,以深入对织物结构的认识,方便导出三维图形,为该类型防弹织物的力学分析提供基础。
1 经编闪避垫纱原理
闪避垫纱[7]是一种纱线运动,又称为躲避垫纱,表现为衬纬梳栉(后梳)与地梳(前梳)的针背横移针距数相等、方向相同时的“部分衬纬”垫纱,处于前梳线圈的主干和延展线之间的衬纬纱不受线圈延长线夹持,在横列的转折处衬纬发生滑移,滑移到前梳的延展线之上并被其阻隔,使后梳衬入的纱线呈直线状浮于地组织的反面,如图1所示。

图1 衬纬滑移组织示例
2 防弹用经编轴向织物结构
防弹用经编轴向织物一般有3个系统的纱线,即衬经纱、全幅衬纬纱和编织纱。衬经纱和全幅衬纬纱之间没有交织,能够平行伸直地形成2个纱线层相互垂直排列并由编织纱捆绑在一起。衬纱主要采用芳纶、高强聚乙烯纤维及玻璃纤维等高性能的无捻纱线,且衬纱的直径要远远大于编织纱,从而使编织纱弯曲而衬纱呈现伸直状态,形成衬经的表面纹理。为了获得紧密的结构,采用多把满穿的衬纬梳栉,梳栉配合构成交替闪避垫纱,又因衬纬纱直径较大,从而形成垂直衬入的衬经纱效果。衬纬垫纱的梳栉起衬经垫纱的作用,增加衬经的横密。2把衬经导纱梳前后配置,交替垫纱。采用德国KARL MAYER公司RS 3 EMS全幅衬纬机开发的KM19990128防弹用经编轴向织物如图2所示。

图2 防弹用经编轴向织物正反面
就理论而言,变化衬纬和经平组织相结合,在衬纬延展线与经平针背垫纱同向且长度相同的情况下,该部分的衬纬纱将会从工艺反面滑移到经平的延展线上面,在不满足此情况的状态下,衬纬纱则会压在前梳延展线下方,从而使衬纬纱交替出现在经平延展线两面,再采用1把全幅衬纬的组织,使织物表面呈现出机织物一样的纹理。但与机织物相比,防弹用经编轴向织物的横向密度较大,织物紧密程度较好;减少了纱线因交织而产生的屈曲不直,只在捆绑纱中存在微量屈曲,在受到外力作用时,平行伸直的增强纱线同时承受载荷,减少了应力集中现象,保证纤维的强力利用率[8],同时可减少纤维用量和织物的质量。Conzellman等[9]将传统的机织物结构与德国KARL MAYER公司开发的KM19990128防弹用经编轴向防弹结构(图2)进行一系列的弹道测试,织物结构类型和规格如表1所示,测试结果如表2所示。结果显示,20层面密度0.584 0 g/cm2的新型芳纶组件织物性能远远优于28层面密度0.618 8 g/cm2的机织物组件。
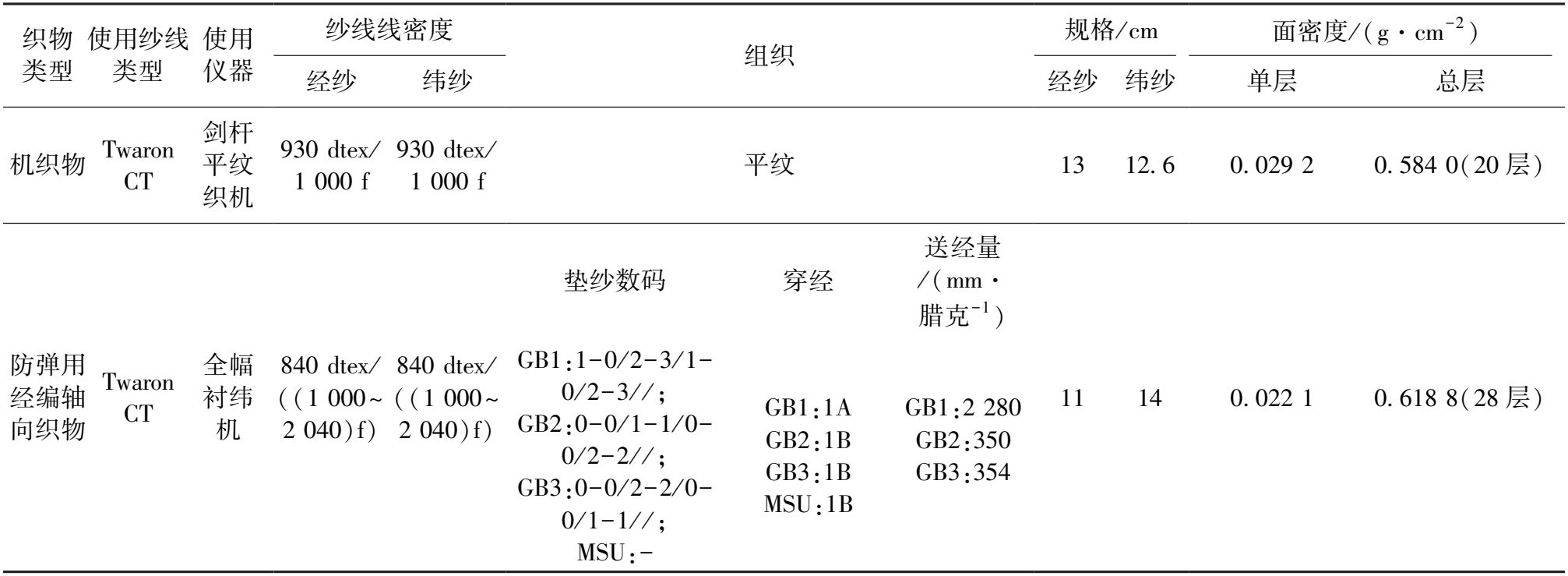
表1 机织与防弹用经编轴向织物测试对比表

表2 机织与防弹用经编轴向织物测试对比表
3 防弹用经编轴向织物模型
影响防弹用经编轴向织物外观的因素主要有垫纱运动和穿经规律[10]。为更好地对其进行研究,有必要建立垫纱数码数学模型和穿经数学模型。
防弹用经编轴向织物线圈结构包括2种,分别是成圈线圈结构和衬纬线圈结构,因此根据各自的结构特征,分别采用一定的控制点来确定线圈的形状建立线圈仿真模型。
3.1 垫纱数码数学模型
垫纱数码模型一般采用单针床垫纱数码的方式表示[11],垫纱数码矩阵(Um)模型如式(1)所示,由此可以推断出线圈的类型、开口闭口及梳栉横移情况。
(1)
式中:n=1,2,…,N;N表示横列数;m=1,2,…,M;M表示梳栉数;u(m,n,1)表示第m把梳栉上第n横列上的第1个数码;u(m,n,2)表示第m把梳栉上第n横列上的第2个数码。
对于线圈的类型,当u(m,n,2)-u(m,n,1)=0时,线圈类型为衬纬线圈;|u(m,n,2)-u(m,n,1)|=1时,线圈类型为普通成圈线圈;|u(m,n,2)-u(m,n,1)|=2时,线圈类型为重经线圈。由于针前与针背作同向垫纱或有针前垫纱但针背横移为0时形成的线圈为开口线圈,针前与针背做反向垫纱形成的线圈称为闭口线圈[12],所以当[u(m,n,1)-u(m,n,2)]×[u(m,n,2)-u(m,n+1,2)]≥0时,为开口线圈;当[u(m,n,1)-u(m,n,2)]×[u(m,n,2)-u(m,n+1,2)]<0时,为闭口线圈。
关于梳栉横移情况,令Q(m,n)=u(m,n,2)-u(m,n+1,1),Q(m,n)表示第m把梳栉上第n横列的针背横移方向和横移数。当Q(m,n)>0时,表示第m把梳栉在第n横列从左向右进行针背垫纱;当Q(m,n)<0时,表示第m把梳栉在第n横列从右向左进行针背垫纱,当Q(m,n)=0时,不进行针背运动;|Q(m,n)|表示针背横移距离。
3.2 穿经数学模型
不同的穿经会得到不同的织物效果,用矩阵数学模型(FMW)表示每把梳栉的穿经循环[13],如式(2)所示。
(2)
式中:j=1,2,…,W;W为完全组织的纵行数;m=1,2,…,M;M为参加编织梳栉的总数;fmj的取值为*,A,B,…,其中*代表对应的导纱针不穿纱,A,B等表示代表导纱针穿入的纱线颜色代号。
将建立的垫纱数学模型和穿经数学模型进行组合,可以得到反映织物效应的数学模型,如式(3)所示。进行编程后,即可得到反映防弹用经编轴向织物的垫纱运动矩阵(ZNW)。
(3)
式中:n=1,2,…,N;N表示花型图的横列数;j=1,2,…,W;W为花型图的纵行数。
3.3 成圈模型
国内外关于成圈模型的研究有很多,基本已趋向于最真实的结构。本文采用Goktepe[14-15]的模型为理论基础,采用多次实验实际测量线圈的各点位置,得出A1~A8共8个点来表示线圈主干的坐标,如图3所示。c、c1、c2、c3为到中心轴的测量横向距离,b、b1、b2为到中心点的纵向距离。开口和闭口线圈的差异可通过后续微调A1、A8的点坐标进行修正来达到预期的效果。

图3 线圈8点模型及侧面图
3.4 衬纬模型
衬纬模型与成圈模型点的确定方式相同,通过2点来确定衬纬的点。以图4左衬纬为例,b3为相邻2行之间的纵向距离。全幅衬纬纱是在衬纬线圈的基础上改变点的坐标位置实现的。
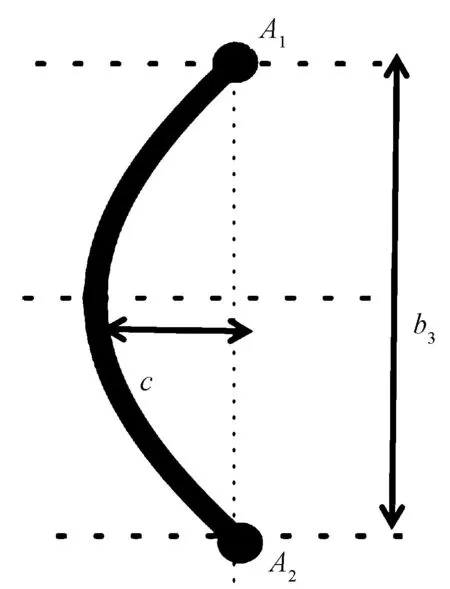
图4 衬纬2点模型
4 衬纬滑移位置判断及偏移量计算
对于防弹用经编轴向织物,衬纬与经平结合,梳栉之间存在针背垫纱大小相同、方向相同的情况,对于这部分的衬纬纱,会滑移到经平的延展线上面。通过设计的垫纱模型,对符合条件的衬纬梳进行设置,可以使衬纬梳符合实际偏移规律。
防弹用经编轴向织物理论与实际形态的差异主要体现在衬纬组织的变形上。由于衬纬梳栉无针前垫纱,只作针背垫纱,纱线被夹持在成圈组织线圈主干和延展线之间[16],所以衬纬纱处于成圈线圈根部时,衬纬线圈主要通过成圈线圈的移动而移动;而对于经过闪避垫纱衬纬横列,处于前梳线圈主干与延展线之间的衬纬纱不能被成功加持,衬纬纱从成圈线圈的根部脱落,滑移到成圈线圈的延展线上面[6]。发生闪避垫纱横列的衬纬梳栉形变的主要来自于衬纬纱上延展线的拉力和纱线摩擦力作用,所以需要分2种情况讨论防弹用经编轴向织物中衬纬纱的偏移规律,而在考虑线圈偏移时,衬纬线圈只在线圈横列方向产生位移,所以仅考虑横向偏移情况。
4.1 判断闪避垫纱位置
由于防弹织物使用全幅衬纬,根据前文设置的垫纱数码数学模型,首先在全幅衬纬中寻找符合闪避垫纱的组织。设定底梳为Mα,衬纬梳为Mβ,满足闪避垫纱的条件为:
(4)
式(4)表示当织物中含有衬纬,衬纬梳与底梳在第nk横列的针背横移方向相同且横移数相等,对符合条件的衬纬横列进行赋值。因为式(4)中所述衬纬梳与底梳在第nk横列的针背横移方向相同且横移数相等,所以满足闪避垫纱条件。对于衬纬梳而言,当Q(Mα,nk)=Q(Mβ,nk)<0,且Q(Mα,nk+1)=Q(Mβ,nk+1)>0时,表示衬纬梳在第nk横列从右向左进行针背垫纱,当衬纬梳在第nk+1横列从左向右进行针背垫纱,完成滑移后线圈左侧横移到下一纵行前梳延展线上面,如图5所示。若Q(Mα,nk)=Q(Mβ,nk)>0,且Q(Mα,nk+1)=Q(Mβ,nk+1)>0时,表示衬纬梳在第nk横列从左向右进行针背垫纱,完成滑移后线圈右侧横移到下一纵行,与上述情况类似。

图5 衬纬滑移情况举例
4.2 衬纬横向位移和形变分析
首先对发生闪避垫纱横列的衬纬梳栉进行受力分析如图6所示,A点已从成圈线圈上脱落,主要受到2根延展线的拉力F1和F2的作用,则作用力FA为:
(5)
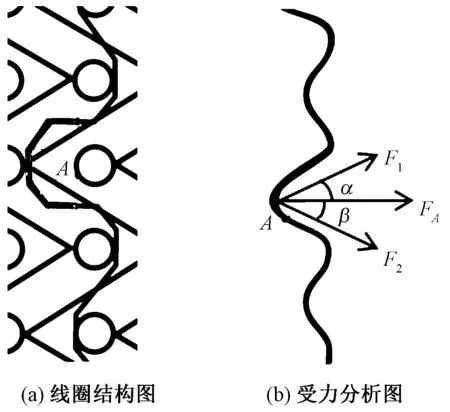
图6 闪避垫纱横列衬纬纱受力横移分析
式中:k1、k2为纱线张力调节系数;n1、n2为与A点相连的2根延展线所跨的针距数;α、β为F1和F2的水平夹角。
根据分析,A点相连的延展线所跨的针距数相等。由式(5)求得衬纬线圈的偏移量DA=(F1cosα+F2cosβ)×k,其中k为线圈偏移数,通过调节k值可以使偏移量DA达到最佳值。
对被成圈线圈穿套起来的衬纬线圈横列进行分析,如图7所示。以B点为例,B点不仅受到衬纬线圈上2根延展线的拉力F3和F4,还受到成圈线圈的延展线摩擦力F5和F6,所以作用力FB计算公式为:
(6)
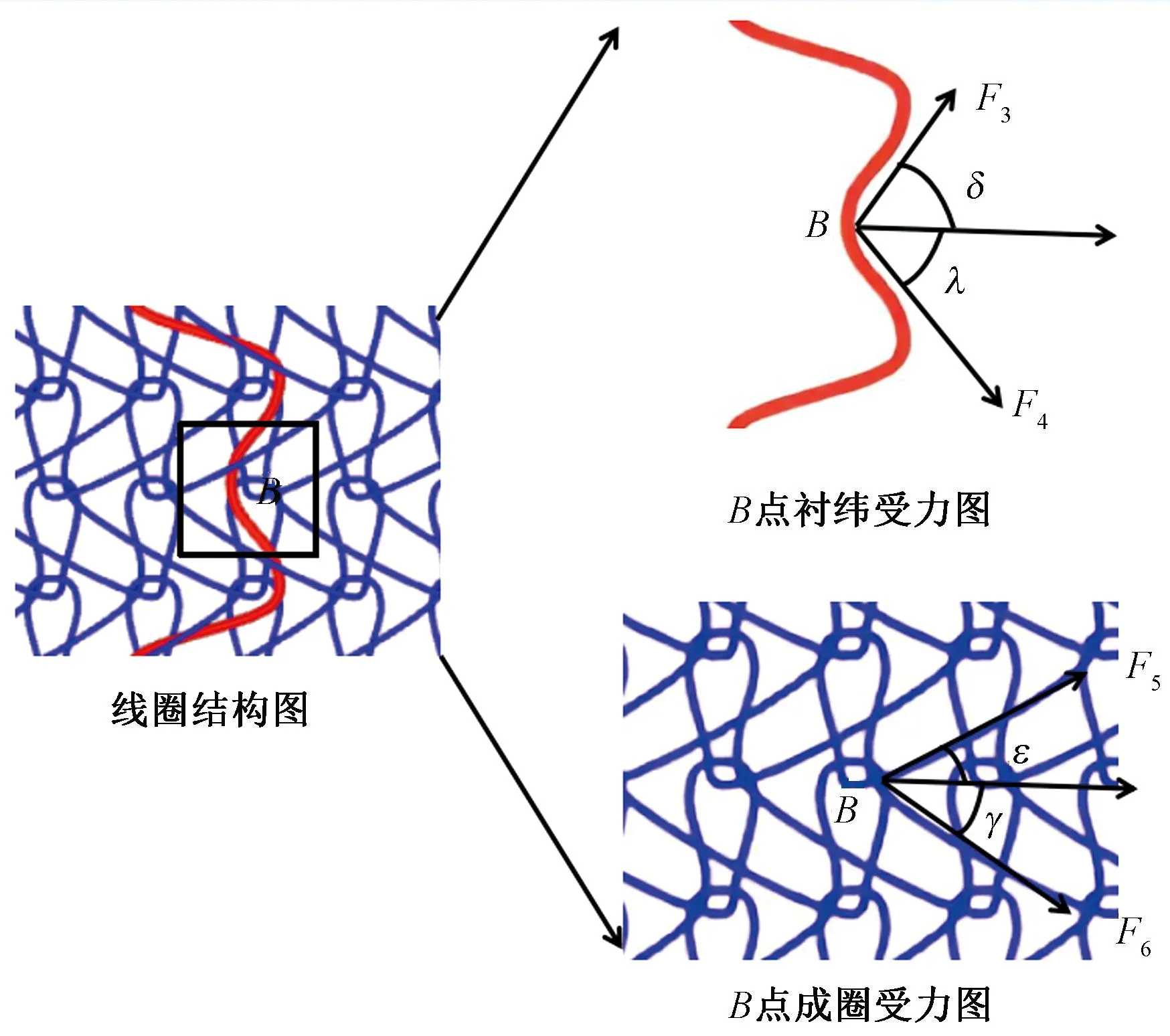
图7 被成圈线圈压住的衬纬纱受力横移分析
式中:k3、k4、k5、k6为纱线张力调节系数;n3、n4为与B点相连的2根延展线所跨的针距数;δ、λ、ε、γ分别为F3、F4、F5和F6的水平夹角。
B点线圈的偏移量DB为:
DB=(F3cosδ+F4cosλ+F5cosε+F6cosγ)k
(7)
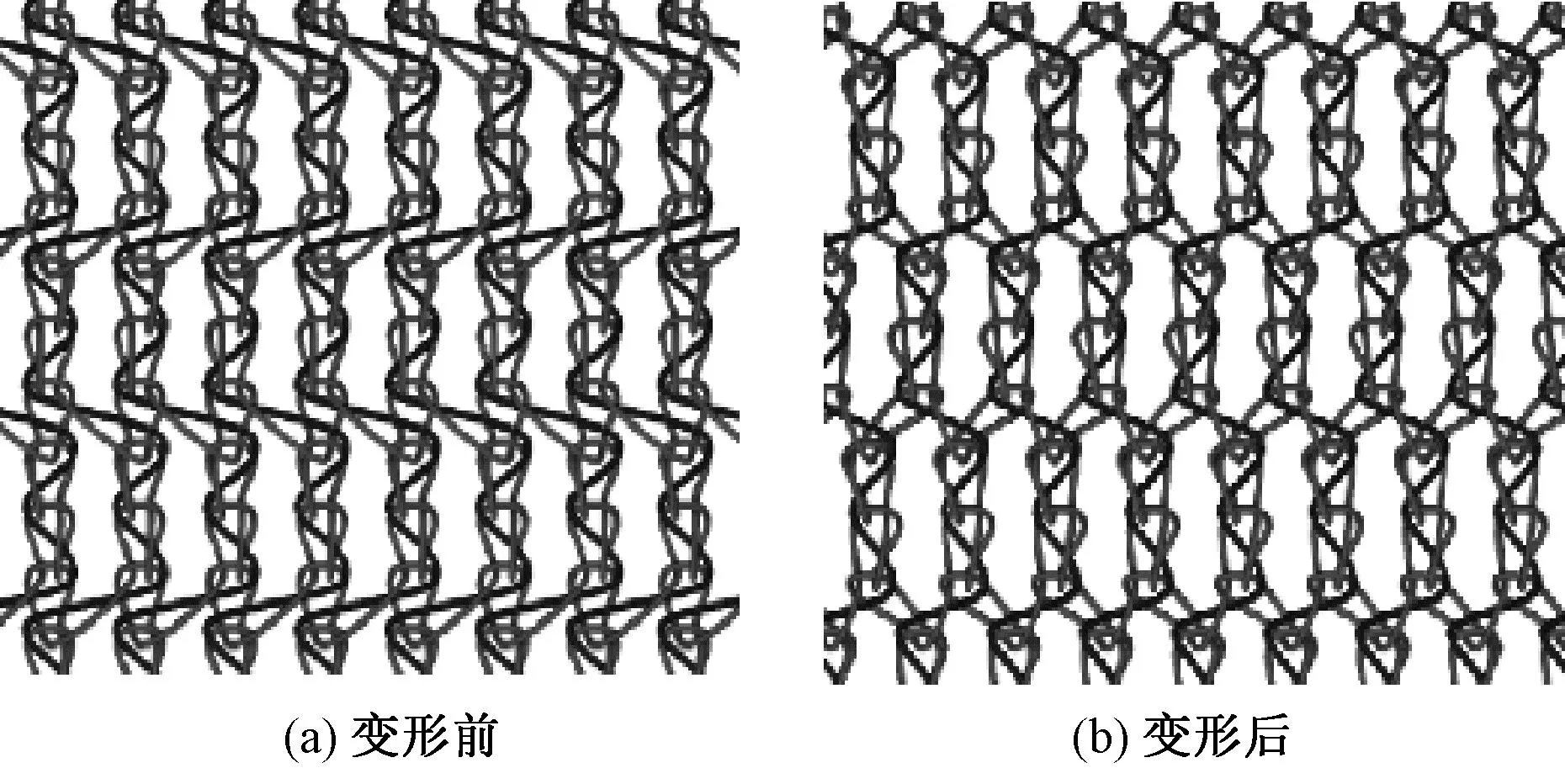
图8 非闪避垫纱的衬纬成圈织物的仿真图
5 防弹用经编轴向织物仿真理论模型实现
以防弹用经编轴向织物的垫纱模型、穿经模型、线圈结构模型和闪避垫纱偏移规律及受力分析为基础,得出防弹用经编轴向织物的仿真理论模型。在仿真过程中,除了要根据上述模型和规律进行仿真外,还要考虑到织物的原料、密度、纱线线密度等因素,可以使用不同的颜色、线密度的模型来表示织物的结构关系。
图9为图2对应的防弹用经编轴向织物仿真图。该仿真主要考虑衬纬组织经过闪避并受力形变后的状态,可以看出仿真图与实际织物的衬纬梳栉较为接近,符合经编防弹轴向织物的理论模型状态。

图9 轴向闪避垫纱防弹织物仿真图
6 结束语
本文在分析轴向闪避垫纱织物的编织和结构特点的基础上,采用JavaScript和C#作为计算机程序设计语言进行计算机编程,对经编防弹轴向织物的结构特征进行描述,根据经编防弹轴向织物的结构分别建立了织物的垫纱模型、穿经模型和线圈模型,通过分析闪避和衬纬受力情况,来实现织物的三维仿真,以便深入认识织物的结构,方便织物的建模,为后续有限元分析打下基础。
本文经编防弹轴向织物中含有闪避垫纱,需要对闪避垫纱的位置进行判断,并分别对闪避垫纱和正常垫纱的衬纬纱进行受力分析,判断衬纬纱的偏移量,通过进行多次调整,达到衬纬纱线仿真图与实物图相近的结果。本文模型进行的仿真均在前台,可以提高仿真速度。
