基于多智能体强化学习的电-碳-绿证多市场均衡研究
2024-01-11马天男向明旭陈玉敏
马天男,向明旭,魏 阳,刘 畅,4,陈玉敏
(1. 国网四川省电力公司经济技术研究院, 四川 成都 610041; 2. 重庆大学电气工程学院, 重庆 400044; 3. 国网四川省电力公司电力科学研究院, 四川 成都 610041; 4. 四川省新型电力系统研究院, 四川 成都 610041)
0 引 言
电力市场机制设计对于推进碳交易市场参与的电力市场建设并加速以绿电为主体的高比例清洁能源电力系统建设具有重要作用,是构建新型电力系统、推进“双碳”战略目标的关键途径[1-2]。中国在2017年发布了《全国碳排放权交易市场建设方案(发电行业)》,指出“按照国家生态文明建设和控制温室气体排放的总体要求,在不影响经济平稳健康发展的前提下,分阶段、有步骤地推进碳市场建设”[3]。同时,发布了一系列的工作方案和管理办法在全国范围内试行绿证交易[4-6]。
电力市场、碳市场与绿证市场之间通过市场机制的作用深刻影响市场主体决策,通过价格联动和供需关系等产生交互影响。3个市场在核心产品属性、政策、技术、市场定位等方面联系密切,机制层面的有效协同将有利于形成合力,共同推动清洁能源发展和行业社会碳减排[7]。因此,研究电力市场、碳市场、绿证市场等各市场之间的耦合分析对于中国电力市场的建设具有重大意义。
电力市场均衡分析方法常采用以市场主体利润最大化为目标的报价决策模型和以社会福利最大化为目标的市场出清模型共同构成的电力市场双层均衡模型[8]。该模型的求解方法为:先基于下层模型的卡罗需-库恩-塔克(Karush-Kuhn-Tucher,KKT)条件和线性化手段,将双层均衡模型转化为带均衡约束的均衡优化模型(equilibrium problem with equilibrium constraints,EPEC);再将模型中的各非线性项线性化处理后进行求解[9]。此外,还可以使用对角化算法求解上述EPEC模型[10-12]。上述模型驱动方法在求解线性模型的电力现货市场均衡解方面取得了显著成效。
然而,在新型电力系统建设背景下,现有的均衡分析模型与求解方法难以满足电力市场机制设计的更高要求。现有的均衡分析方法,特别是EPEC方法,受KKT条件的限制,其建模过程难以考虑发电机组成本和运行特性的非凸性,并且模型线性化过程中产生的互补松弛条件数量随系统规模和机制复杂程度的增加而迅速增长,导致该方法在解决大规模系统和复杂机制下的市场均衡问题时面临巨大挑战。同时,上述模型本质上是一种完全信息博弈问题,每个市场主体都知晓其他主体以及市场出清的全部信息,这与实际电力市场的有限信息环境不符。因此,亟需改进和完善均衡分析方法,以有效解决电力市场建设面临的复杂机制设计问题。
为此,有学者尝试使用数据驱动的强化学习算法求解电力市场均衡问题[13-14]。强化学习方法的无模型、自主学习等特征与电力市场均衡分析的研究需求相契合,市场主体可以通过与出清环境的不断交互,逐渐学习其最佳策略,不依赖对市场出清环境和其他市场主体策略的了解,只依赖于自身运行特性和观测到的市场出清结果[15],从而避免了模型构建与转化的复杂过程。
下面采用多智能体深度强化学习作为电力市场均衡分析方法,来探讨碳市场与绿证市场交易机制对电力市场均衡的影响。首先,对电力市场均衡模型进行阐述,并采用以最小化购电成本为目标的电力市场双层优化模型,为后续分析碳市场与绿电市场对电力市场的耦合影响奠定模型基础;然后,建立了电力市场与碳市场的联合出清模型、电力市场与绿证市场的联合出清模型以及电-碳-绿证多市场的联合出清模型;最后,提出了基于多智能体深度强化学习的电力市场均衡求解算法,经过验证可有效获取市场均衡解。
1 电-碳-绿证市场均衡研究
1.1 电-碳市场双层优化模型
碳市场的建设会对电力系统产生较大影响。考虑碳市场耦合的电力市场均衡研究是市场机制设计的重要一环,对此提出了电-碳市场双层优化模型。
碳交易市场的参与主体仅包含常规能源发电商,不包含可再生能源发电商。所提模型中,可再生能源发电商仅参与电力日前市场获取收益,常规能源发电商同时参与电力日前市场和碳市场获取收益。因此,电-碳市场双层优化模型包含可再生能源利润最大化模型、常规能源发电商利润最大化模型和日前电力市场出清模型3个部分。
1.1.1 上层模型1:可再生能源发电商利润最大化
目标函数为最大化可再生能源发电商的利润,即日前市场出清的收益减去其发电成本,约束为限制发电商的报价范围。

(1)
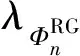
1.1.2 上层模型2:常规能源发电商利润最大化
常规能源机组发电过程中会产生二氧化碳排放,其碳排放量由式(2)计算,机组的碳排放成本由式(3)计算。若机组的碳排放大于免费碳配额,即碳排放成本为正,则发电商需要从碳排放权市场中购买所需的碳排放权;若机组的碳排放小于免费碳配额,即碳排放成本为负,则发电商可在碳排放权市场中出售剩余的碳排放权。
e=φP
(2)
CCET=pCET(e-ef)
(3)
式中:e、φ、CCET分别为常规能源机组的碳排放量、碳排放强度和碳排放成本;pCET为碳排放权市场中的碳价;ef为免费碳排放配额。
常规能源发电商的利润最大化模型如式(4)所示,目标函数为最大化常规能源发电商的利润,即日前市场出清的收益减去其发电成本和碳排放成本,约束为限制发电商的报价范围。
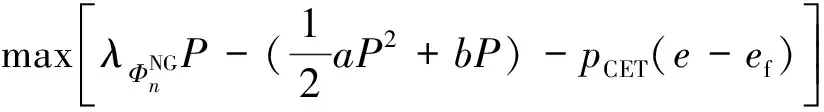
(4)
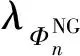
1.1.3 下层模型:日前电力市场出清
日前电力市场出清模型如式(5)—式(8)所示。目标函数式(5)为最小化总发电成本,也称作最大化社会福利;式(6)为节点功率平衡约束;式(7)为机组出力上下限约束;式(8)为支路潮流约束。
(5)
(6)
(7)
-Sn,m≤Bn,m(θn-θm)≤Sn,m
(8)
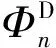
1.2 电-绿证市场双层优化模型
考虑绿证市场耦合的电力市场均衡研究是市场机制设计的重要一环,因此提出了电-绿证市场双层优化模型。
绿证交易市场的参与主体仅包含可再生能源发电商,常规能源发电商不参与其中。所提模型中,常规能源发电商仅参与电力日前市场获取收益,可再生能源发电商同时参与电力日前市场和绿证市场获取收益。因此,电-绿证市场双层优化模型包含可再生能源利润最大化模型、常规能源发电商利润最大化模型和日前电力市场出清模型3个部分。
1.2.1 上层模型1:可再生能源发电商利润最大化
在电力市场中出清后,根据可再生能源发电商的发电量为其颁发相同数量的绿证,可再生能源发电商可在绿证市场中将其出售,出售绿证获得的收益由式(9)计算。
RTGC=pTGCP
(9)
式中:RTGC为可再生能源发电商出售绿证获得的收益;pTGC为绿证价格。
可再生能源发电商的利润最大化模型如式(10)所示,目标函数为最大化可再生能源发电商的利润,即日前市场出清的收益加上在绿证市场交易的收益减去其发电成本,约束为限制发电商的报价范围。

(10)
1.2.2 上层模型2:常规能源发电商利润最大化
目标函数为最大化常规能源发电商的利润,即日前市场出清的收益减去其发电成本,约束为限制发电商的报价范围。
s.t.b≤bbid≤bmax
(11)
1.2.3 下层模型:日前电力市场出清
电-绿证市场双层优化模型的下层模型同第1.1.3节。
1.3 电-碳-绿证市场双层优化模型
所建的电-碳-绿证市场双层优化模型如图1所示:上层为发电商利润最大化模型,求解得到发电商在日前市场中的报价策略传递给下层模型;下层为日前市场、碳市场、绿证市场出清模型,求解得到日前市场的节点电价和各发电商出清电量、可再生能源发电商颁发绿证数量、常规能源发电商碳排放量等市场出清结果传递给上层模型。在所建模型中,可再生能源发电商参与电力日前市场和绿证市场获取收益,常规能源发电商参与电力日前市场和碳市场获取收益。因此,电-碳-绿证市场双层优化模型包含可再生能源利润最大化模型、常规能源发电商利润最大化模型和日前电力市场出清模型3个部分。
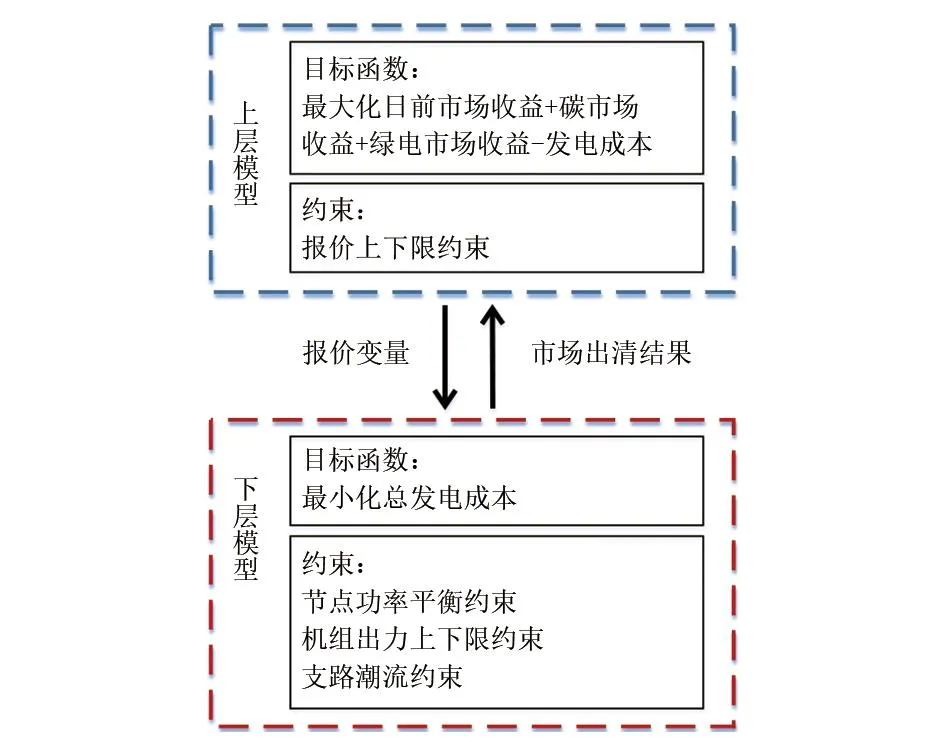
图1 电力市场双层优化模型
1.3.1 上层模型1:可再生能源发电商利润最大化
目标函数为最大化可再生能源发电商的利润,即日前市场出清的收益加上绿证市场的收益减去其发电成本,约束为限制发电商的报价范围。

(12)
1.3.2 上层模型2:常规能源发电商利润最大化
目标函数为最大化常规能源发电商的利润,即日前市场出清的收益减去其发电成本和碳排放成本,约束为限制发电商的报价范围。
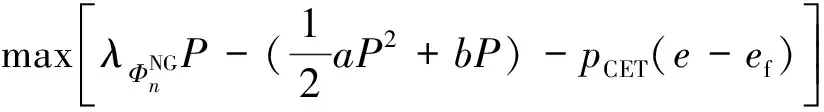
(13)
1.3.3 下层模型:日前电力市场出清
电-碳-绿证市场双层优化模型的下层模型同为第1.1.3节,此处不再赘述。
2 基于多智能体深度强化学习的电力市场均衡求解方法
2.1 多智能体双延迟深度确定性策略梯度算法
在电力市场均衡问题中,每个市场参与主体都被建模为智能体,因此在系统中存在多个智能体,各智能体之间的行为会相互影响,共同推动整个系统的演化。为了解决电力市场中的多智能体系统演化问题,多智能体强化学习(multi-agent reinforcement learning)方法被广泛采用。多智能体双延迟深度确定性策略梯度(multi-agent twin delayed deep deterministic policy gradient, MATD3)算法是一类多智能体强化学习方法。智能体系统中,多个智能体处于相同的环境中,它们分别独立与环境交互,利用环境的反馈奖励更新自身策略。MATD3T算法在解决电力市场的多智能体系统问题中表现出了较好的性能。MATD3算法包括策略网络和价值网络。其中,策略网络的输入是智能体i对环境的观测oi及决策变量θi,输出动作ai=μ(oi;θi)控制智能体i的行为。价值网络的输入是所有k个智能体的观测,即全局状态s={o1,o2,...,ok},输出q(s,a;ωi)用于评价智能体i动作的优劣,可以指导策略网络改进其策略。MATD3算法分别训练策略网络与价值网络,训练数据是从经验回放池中取出t时段的四元组(st,at,rt,st+1),如式(14)—式(17)所示。
(14)
(15)
(16)
(17)
式中:st为t时段的全局状态;at为t时段的输出动作;rt为t时段的奖励回报。
训练策略网络μ(oi;θi)的目标是提高价值网络,对智能体i的打分q(s,a;ωi),如式(18)所示。对策略网络的目标做蒙特卡洛近似并求梯度,然后做梯度上升更新参数θi,如式(19)—式(20)所示。
Ji(θ1,...,θk)=
ES{q[S,{μ(o1;θ1),...,μ(ok;θk)};ωi}
(18)
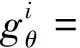
(19)
(20)
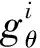
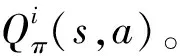
(21)
(22)
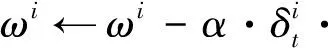
(23)

2.2 基于多智能体深度强化学习算法的模型求解算法
使用MATD3算法求解电力市场均衡,电力市场环境下的强化学习要素设置如下:
1)智能体(Agent):参与电力市场的所有发电商都被设置为智能体,假设系统中共有k个发电商。
2)环境(Environment):将环境定义为电力市场的出清过程,在发电商报价后电力市场进行出清并将出清结果反馈给发电商。
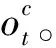


基于MATD3算法求解电力市场均衡模型的具体步骤如下:
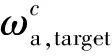
3)按照训练频率定期更新网络参数。从经验回放池中随机抽样一个四元组的mini-batch,对于各发电商计算其目标策略网络和目标价值网络的输出,并根据目标网络对价值网络和策略网络的参数ωa、ωb、θ进行更新。
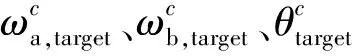
3 算例研究
3.1 多智能体强化学习算法有效性验证
采用经过修改的IEEE 30节点测试系统进行分析验证。该系统有30个节点、41条支路、20处负荷和6台发电机组,其中:机组G1和G2为风电机组,由可再生能源发电商持有;机组G3—G6为常规能源机组,由常规能源发电商持有。发电机组参数见表1。

表1 发电机组参数
使用第1.2节中双层优化模型和强化学习算法对测试系统的市场均衡进行求解,训练过程如图2所示。训练过程共30 000步,前10 000步为随机生成动作,以获得尽可能多的观测状态作为策略网络和价值网络的训练数据;后20 000步智能体根据策略网络生成报价动作,智能体的价值网络和策略网络不断训练更新,策略网络逐渐学习到最优报价策略,最后生成稳定的报价动作。从图2可以看出随着训练进行各智能体的报价逐渐趋于收敛。
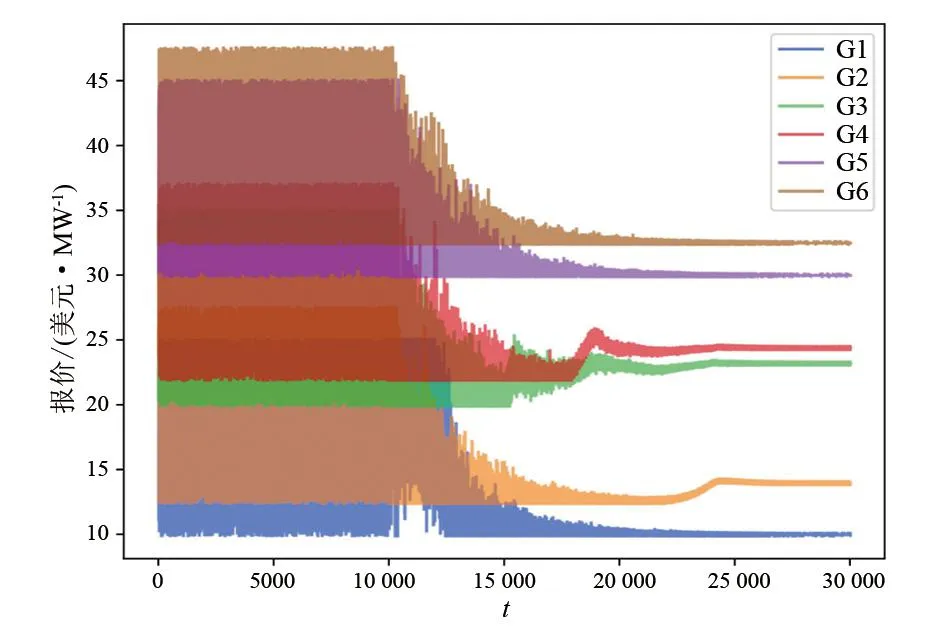
图2 强化学习算法求解市场均衡训练过程
3.2 运行结果分析
3.2.1 碳排放配额及碳价对市场均衡点的影响
为探究碳配额对市场均衡点的影响,设置ef为30 t、20 t、10 t分别对应碳配额宽松、碳配额适度收紧和碳配额严重收紧3种场景。同时,为探究碳价对市场均衡点的影响,设置pCET从0 至20 美元/t以步长2 美元/t递增。
碳配额和碳价对市场出清电价的影响如图3所示,其中场景1、场景2、场景3分别对应于碳配额宽松、碳配额适度收紧和碳配额严重收紧的场景。

图3 不同碳配额和碳价下的市场出清电价
从图3中可以看出,出清电价随碳价的升高呈上升趋势。这是因为随着碳价的升高,高排放机组发电需要花费更高的成本从碳市场中购买碳排放权,其总利润降低,因此持有高排放机组的发电商希望通过上报高于发电成本的价格以提高日前电力市场出清电价,从而增加其在电力市场中获得的利润。
在3个碳配额场景中:碳配额适度收紧时,市场出清电价的抬升相对较小,仅高排放机组有动力虚报成本;碳配额严重收紧时,低排放机组也需要购买碳排放权,同时高排放机组的发电利润甚至可能小于购买碳排放权的成本,因此,在该场景的仿真中常规能源发电商都存在虚报成本的行为,电价抬升较大;碳配额宽松时,碳市场对机组的发电约束较小,在碳价较低时碳市场对发电商的报价影响不大,而在碳价较高时发电商可从碳市场中交易获得较高利润,因此在该场景的仿真中,发电商倾向于在碳市场中交易,均选择在电力市场中虚报成本,导致出清电价急剧抬升。
3.2.2 绿证价格对市场均衡点的影响
为探究绿证价格对市场均衡点的影响,设置pTGC从0 至10 美元/张以步长1 美元/张递增。不同绿证价格下可再生能源发电商报价以及市场出清电价如图4所示。由图4可以看出,随着绿证价格的上升,可再生能源发电商的报价逐渐降低,最终趋于上报真实发电成本。其主要原因是可再生能源发电商在绿证市场中的收益取决于其实际发电量,若上报较高的价格,可能会使其成为边际机组导致发电量减少,从而也导致其在绿证市场的收益减少。
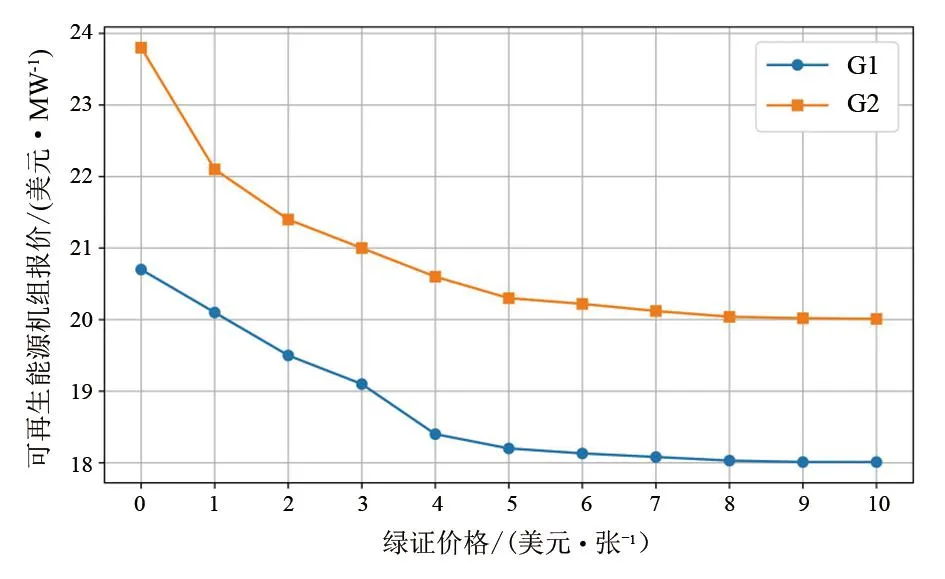
图4 不同绿证价格下的可再生能源发电商报价
3.2.3 碳价与绿证价格对市场均衡点的耦合影响
为探究碳价和绿证价格对市场均衡点的影响,设置碳价从0 至20 美元/t以步长5 美元/t递增,设置pTGC从0 至10 美元/张以步长2.5 美元/张递增,设置碳配额为适度收紧场景。
碳价和绿证价格对市场均衡点的影响如图5所示。可以看出,市场出清电价随碳价上升而升高,随绿证价格上升而降低。
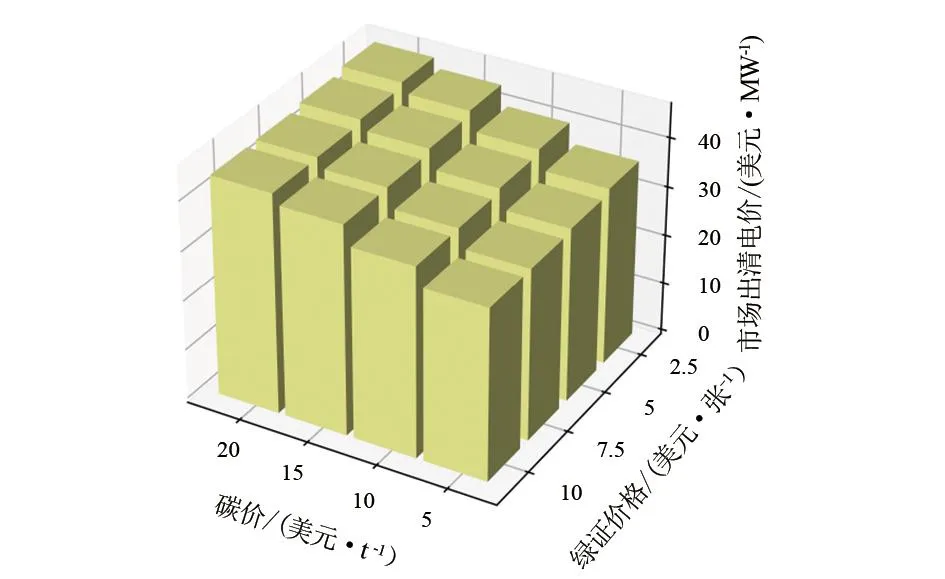
图5 不同碳价和绿证价格下的市场出清电价
为了进一步研究碳价与绿电价格对发电商报价策略的耦合影响,仿真分析了不同碳价与绿证价格下可再生能源机组G1、低排放机组G5和高排放机组G3的报价,如图6—图8所示。在高碳价场景下,低排放机组倾向于在碳市场中获利,高排放机组希望抬升出清电价以增加利润,因此常规能源机组都有动力上报更高的价格。常规能源机组虚报成本使得可再生能源机组也具有上报更高价格的倾向,此时绿证市场的参与增加了可再生能源机组对自身发电量削减的风险厌恶程度,消除了其上报高价的倾向。由此得出,碳市场的参与增加了发电商在电力市场报价中使用市场力的倾向,绿证市场的参与降低了发电商在电力市场报价中使用市场力的倾向。
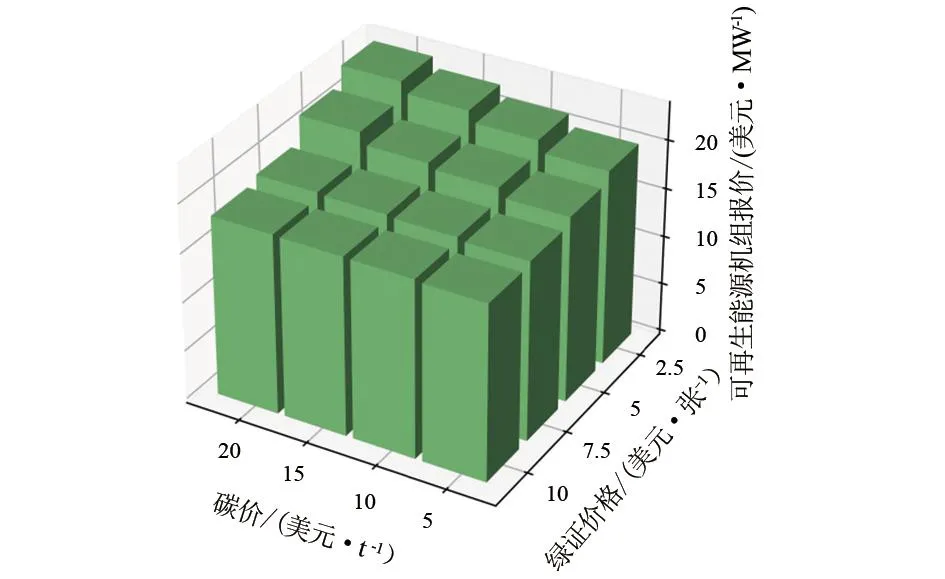
图6 不同碳价和绿证价格下的可再生能源机组报价
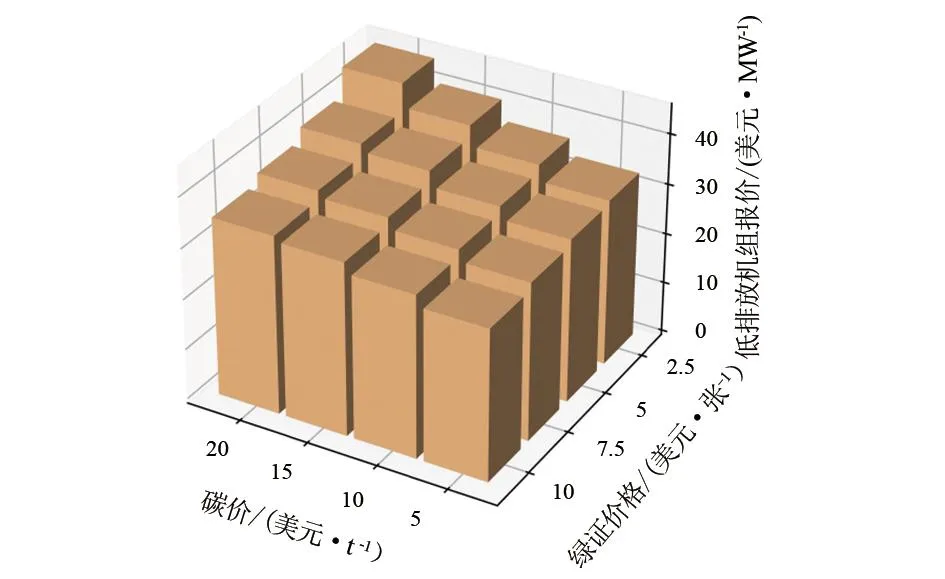
图7 不同碳价和绿证价格下的低排放机组报价

图8 不同碳价和绿证价格下的高排放机组报价
4 结 论
上面在电力市场环境下,根据碳市场与绿证市场的交易规则分别建立了电-碳市场、电-绿证市场和电-碳-绿证市场的双层优化模型,采用强化学习方法对市场均衡进行求解,并就碳市场和绿证市场对电力市场运行的影响进行了探讨。所得主要结论如下:
1)设置适度收紧的碳配额以及适当的碳价能够增加低排放机组的利润,有效激励低排放机组的发电意愿,对电力系统的减排作用较大;严重收紧或宽松的碳配额不能有效激励低排放机组发电,对电力系统的减排作用较小。此外,过高的碳价会导致电价飙升,扰乱电力市场运营秩序。
2)绿证市场的参与可以增加可再生能源发电商的利润,激励可再生能源机组发电,放弃其在电力市场中的市场力,从而降低市场出清电价。
3)市场出清电价和碳价成呈正相关,和绿证价格呈负相关,当前电力系统环境下电价受碳价的影响相对较大;碳市场的参与促进发电商在电力市场中使用市场力,而绿证市场的参与限制发电商在电力市场报价中使用市场力。
