计及分布式光伏安装面积限制的配电网储能系统与线路扩容联合规划

邵晨颖,李沛霖,杨新婷,刘友波

( 1. 四川大学电气工程学院,四川 成都 610065;2. 国网四川省电力公司经济技术研究院,四川 成都 610041)

0 引 言

为了满足日益增长的负荷需求,配电网需要进行动态扩容规划,计及政治、经济、地理等因素,在最小化成本的同时尽可能保证系统的技术指标不受影响[1-2]。然而,随着分布式光伏广泛部署在低压配电网中[3],其随机波动的输出使配电网的光伏支撑能力趋近饱和,产生弃光等问题,光伏的消纳将成为新型配电网在规划运行中需要重点研究的问题之一[4]。另一方面,储能系统因具有良好的调峰能力和抑制新能源出力波动的作用,在配电网中得到大规模应用。从规划角度出发,装设储能系统可以避免使用增加冗余容量方法解决负荷增长和峰谷差加剧的问题,有助于提升设备资产利用率,延缓配电网升级改造,推动电网的高可靠性连续供电发展[5]。因此,考虑将优化储能配置同线路扩容结合起来作为应对负荷增长的规划手段,同时在主动配电网动态规划过程中计及光伏的消纳情况,这对实现配电网的清洁、经济、可靠运行非常重要。

配电网扩容规划作为配电网中的一个重要研究方向,如今已有不少研究成果。文献[6]提出了一种考虑负荷增长、电价、扩容投资成本、运营成本等因素的配电网扩容规划方法。文献[7-8]针对电动汽车负荷的发展,构建了配电网扩容与电动汽车充电站协调规划模型。文献[9]考虑了配电网投资和分布式电源投资,文献[10]计及热、电需求和分布式电源的不确定性,二者都将配电网多阶段扩容规划问题建模为一个混合整数线性规划优化问题。值得注意的是,上述研究大多忽略了储能系统接入后对配电设备利用率的提升作用。因此,储能配置在电网规划过程中的替代潜力近年来引起了众多学者的关注。文献[11-12]提出了储能系统接入的经济效益模型,对储能系统削峰填谷带来的经济效益实现了度量计算。文献[13]通过潮流灵敏度搜索优先选择重过载的配电设备进行储能配置。文献[14]综合考虑了储能系统对电网的削峰填谷作用和经济成本,提出一种实现储能功率、容量配置及运行调度的方法。上述文献均只使用储能配置进行单阶段的规划研究,然而配电网规划过程往往不是独立的,需要涉及多个阶段进行综合规划,且储能配置的替代效益是有限的,在实际的规划过程中,传统的扩容规划需要同储能配置结合起来使用。因此,文献[15]提出了一种与储能配置相结合的多阶段主动配电网规划模型,分析了储能系统带来的供电可靠性提升效果。文献[16]在规划时考虑了负荷的不确定性,在实现电网安全运行和电网损失最小化的同时,保证主动配电网能够按照调度计划运行。但储能系统对提升光伏消纳率、减少弃光方面的效用还没有被考虑到规划目标中。

因此,下面将储能配置与传统扩容方法结合起来对主动配电网进行多阶段的动态规划,以经济性最佳为目标,将光伏消纳转化为环境效益计入目标函数中,同时利用Logistic曲线模拟分布式光伏在一定安装面积限制下的“S”型发展曲线,实现了考虑分布式光伏区域容量上界的配电网线路扩容与储能配置的双重优化,有助于在满足客观电力需求约束下实现资金的高效利用。

1 考虑安装面积限制的分布式光伏发展模型

随着分布式光伏的不断发展,规划区域内可供分布式光伏铺设的空间日益减少,其装机总量将逐步趋向饱和[17]。总体来说,分布式光伏的发展曲线大致呈“S”型。因此,可以基于Logistic曲线构建考虑安装面积限制的分布式光伏发展模型,预测各规划阶段的光伏装机容量及出力曲线,作为后续联合规划的基本边界条件。步骤如下:

1)根据土地利用性质进行分区,分为商业区、住宅区和工业区,然后根据各区域的屋顶面积,在给定屋顶有效利用率和单位面积饱和光伏容量密度下,估计各分区的光伏饱和装机容量。

(1)

分布式光伏组件型号确定后,单位面积的最大可装设光伏容量将随之确定,从而得到相应的单位面积饱和光伏容量密度。同时,不同区域的屋顶有效利用率取值如表1所示。

表1 不同区域的屋顶有效利用率

2)不同区域的分布式光伏发展情况也有所不同,因此采用Logistic函数拟合光伏累计安装发展的“S”曲线。

(2)

式中:ξi,n为区域i在第n个规划阶段的光伏安装普及率;ai、bi、ci均为区域i的拟合系数,可以依据该地区其余网格相应土地性质的光伏发展历史数据或专家经验来确定。

基于步骤1得到的饱和装机容量,可以计算各规划阶段的光伏装机容量为

(3)

式中,PPV,i,n为区域i在第n个规划阶段的光伏装机容量。

3)记初始年不同场景下的光伏典型出力曲线为光伏出力基准曲线,则不同区域在不同规划阶段的各场景下光伏出力曲线可以大致估计为

(4)

(5)

式中:PPV,i,0为初始年区域i的光伏装机容量;I为所分区域总数。

2 配电网储能配置与线路扩容联合动态规划模型

下面将配电网联合规划经济性最优作为目标,构建面向典型场景的配电网储能配置与线路扩容联合动态规划模型。

2.1 目标函数

基于经济性的协调规划目标函数可以表示为:

(6)

Cs=Cenv,s+Callowance,s-CESS,s-CLine,s

(7)

式中:F为协调规划的目标;m为场景数;ωs为场景s出现概率;Cs为场景s的经济性;Cenv,s、Callowance,s、CESS,s、CLine,s分别为场景s下光伏消纳与储能系统接入带来的环境收益、储能系统削峰填谷补贴收益、储能成本和线路扩容成本。

2.1.1 环境收益

升级改造线路以扩大线路容量并配置储能系统,有助于提高光伏的消纳率,减少火电机组出力,降低各类污染物的排放,从而带来一定的环境收益。

(8)

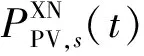
2.1.2 补贴收益

储能系统接入后,能通过调整其充放电状态和功率有效平抑电网的峰谷差,具有削峰填谷的作用。政府为激励储能系统参与削峰填谷,出台了一系列政策给予相应补贴,其经济效益可以表示为

(9)

式中,rbt为政府对转移单位峰荷给予的补贴。

2.1.3 储能成本

(10)

(11)

(12)

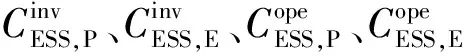
2.1.4 线路扩容成本

参考文献[18],以资本年化率的方式对线路扩容投资成本进行定义,即

(13)

式中:rLine和LLine分别为最低预期资本回收率和规划年限;Nkr,s和cl,s分别为场景s下需要扩容线路数和线路l的扩容单价;Ll为线路l的长度。

2.2 约束条件

2.2.1 潮流约束

(14)

(15)

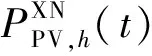
2.2.2 储能约束

储能系统的充放电功率约为

(16)

储能系统的荷电状态约束为

(17)

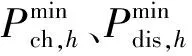
2.2.3 网络运行约束

(18)

2.2.4 规划连续性约束

(19)

式中:EESS,h,n和EESS,h,n-1分别为第n个和第n-1个规划阶段下节点h处储能系统的配置容量;Igh,max,n和Igh,max,n-1分别为第n个和第n-1个规划阶段下线路g-h的电流上限。

3 凸松弛优化的联合规划模型及其求解

第2章构建的联合规划模型中存在决策变量的乘积和平方项,导致规划模型因非凸非线性而难以求解。基于此,采用大M法、相角松弛与二阶锥松弛,将模型中所有非凸约束进行凸化处理,最终将原始问题转化为混合整数二阶锥规划问题,从而便于使用Gurobi等商业求解器求解。

3.1 潮流约束凸松弛

通过相角松弛去掉电流、电压的相角,保留幅值,同时进行二阶锥松弛扩大可行域,可以得到潮流约束式(14)的凸化形式[19],如式(20)—式(22)所示。

(20)

Vh(t)=Vg(t)-2[rghPgh(t)+xghQgh(t)]+

(21)

(22)

式中:rgh和xgh分别为线路g-h的电阻、电抗;Vh(t)、Vg(t)分别为时刻t节点h和g的电压幅值的平方;Agh(t)为时刻t线路g-h的电流幅值的平方。

3.2 储能约束凸松弛

基于大M法对式(16)的储能系统充放电功率约束进行松弛,可得:

(23)

式中,M为一个足够大的数,此处取99 999。

4 算例分析

4.1 算例基本数据

下面以四川省某实际网格下3条10 kV线路组成的网络为规划区域,验证所提规划方法的效果。经过实际调研,基于台区下所带用户的土地性质对待规划线路进行分区,如图1所示。

图1 某实际网格下3条10 kV线路构成的拓扑分区

该网格的光伏出力和负荷典型场景如图2所示,3个场景可以大致认为是晴天(场景1)、多云(场景2)和阴雨(场景3)天气下的光伏出力和负荷典型日曲线。3种场景比例分别为15%、60%和25%。

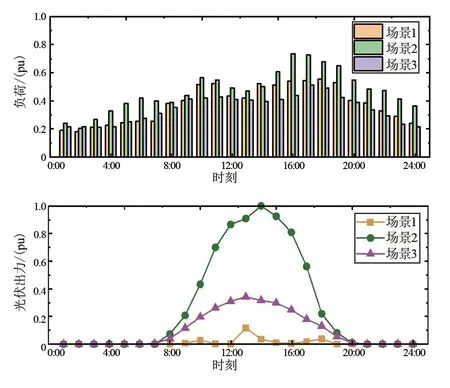
图2 光伏出力和负荷典型场景

假设2026年该网格分布式光伏容量达饱和,以2021年为现状年,估计2022—2026年期间的光伏容量发展情况。首先对该规划线路远景年分布式光伏饱和装机容量进行预测,由调研得到的各区域屋顶面积,根据式(1),取单位面积饱和光伏容量密度为202.3 W/m2,可知各区域分布式光伏饱和装机容量如表2所示。

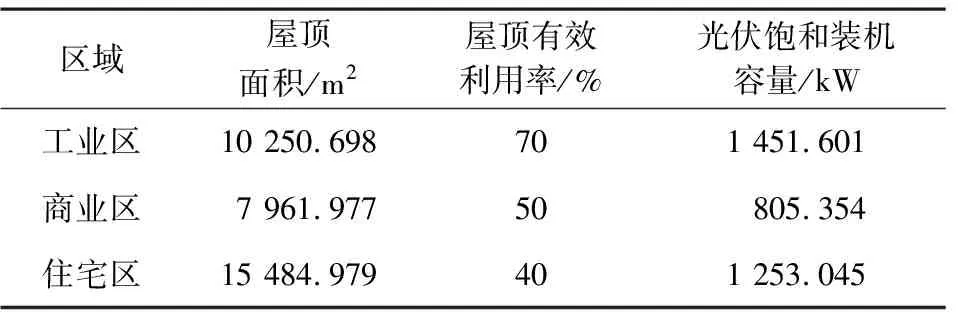
表2 各区域屋顶面积及分布式光伏饱和装机容量

接着由饱和装机容量求取各规划阶段装机容量,计及不同区域的土地性质,用不同Logistic曲线模拟不同区域的光伏发展情况。

(24)

(25)

(26)

式中,ξindustrial,n、ξcommercial,n、ξresidential,n分别为工业区、商业区、住宅区在第n个规划阶段的光伏安装普及率。

计及上述分布式光伏的发展情况,考虑工业区、商业区和住宅区负荷分别按10%、8%、5%的年增长率进行增长,在此基础上进行线路扩容和储能配置的联合规划。可供选择的储能配置与线路扩容的参数如表3所示,所建模型中的投资和收益计算相关参数取值如表4所示。

表3 可供选择储能配置与线路扩容参数

表4 模型相关参数

4.2 联合规划结果

由于需要对该网格进行为期5年的规划,可以将规划过程以年为单位分成5个规划阶段,利用Matlab+Gurobi对每个规划阶段进行一次模型求解。由于使用了二阶锥松弛,通过计算二阶锥误差可以判断结果的可信度,二阶锥误差计算方式为

(27)

式中,ε为二阶锥误差。

优化后的二阶锥误差如图3所示,可以看出,二阶锥误差非常小。这说明二阶锥松弛后该模型的优化结果是足够可信的。

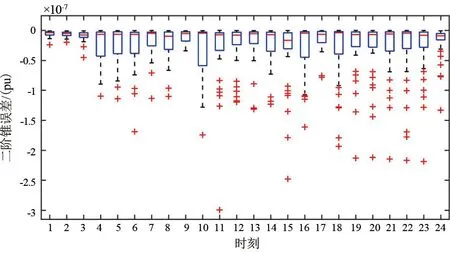
图3 二阶锥误差

经求解得到的各阶段的储能配置和线路平均容量规划结果如表5所示。其中,规划前线路的平均容量为2.823 6 MW。线路平均容量的计算公式为

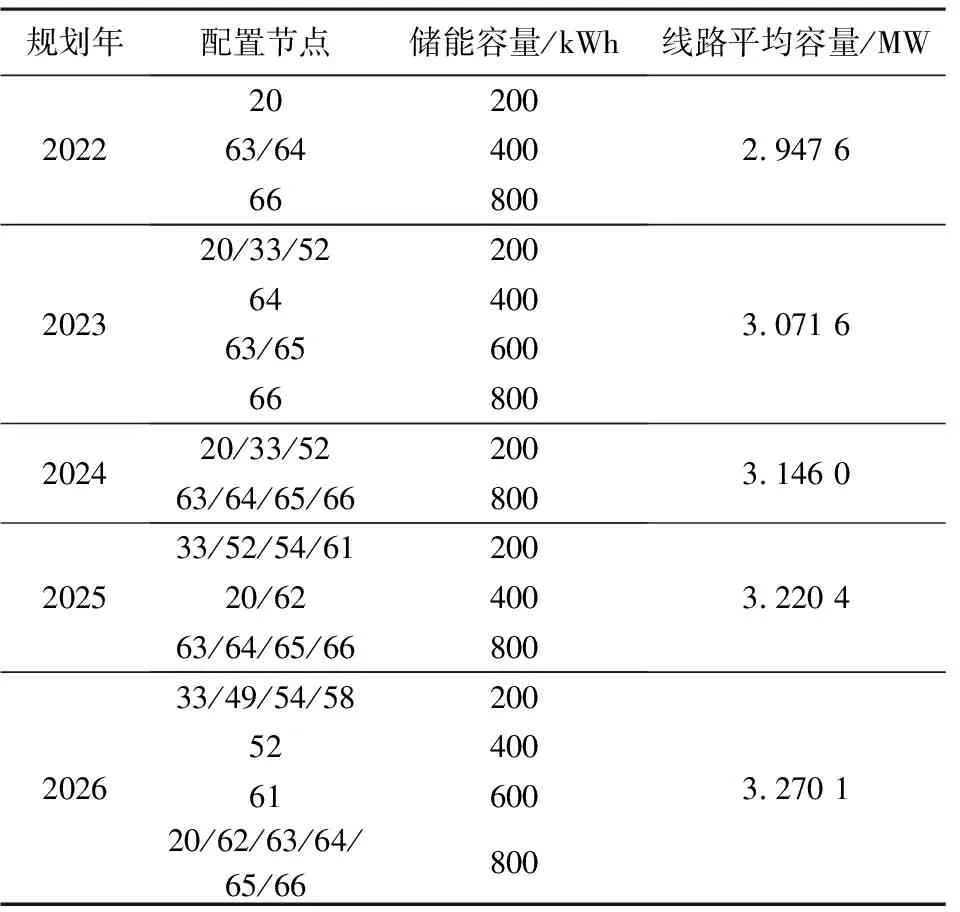
表5 各阶段的储能优化配置和线路平均容量规划结果

(28)

各阶段的线路扩容方案如图4所示。

图4 各阶段的线路扩容方案

从规划结果可以看出:随着规划年限的增长,需要配置储能的节点越多,相应地,储能配置容量也越大;与此同时,线路的平均容量也因部分线路的扩容在逐年提高。

4.3 联合规划效果验证

为了证明联合规划对配电网可靠性的提升作用,选用系统平均停电持续时间指标(system average interruption duration index,SAIDI)、系统平均停电频率指标(system average interruption frequency index,SAIFI)和系统平均供电可用率指标(average service availability index,ASAI)来评估系统的可靠性[20-21],并采用序贯蒙特卡洛法进行可靠性的计算。同时,以峰谷差率为指标,体现储能配置带来的削峰填谷效用,其计算公式为

(29)

式中:φfg为峰谷差率;Nbus为节点数。

将所提线路扩容与储能配置的联合规划方法和仅进行线路扩容的传统规划方法效果进行对比,结果如表6、表7所示。

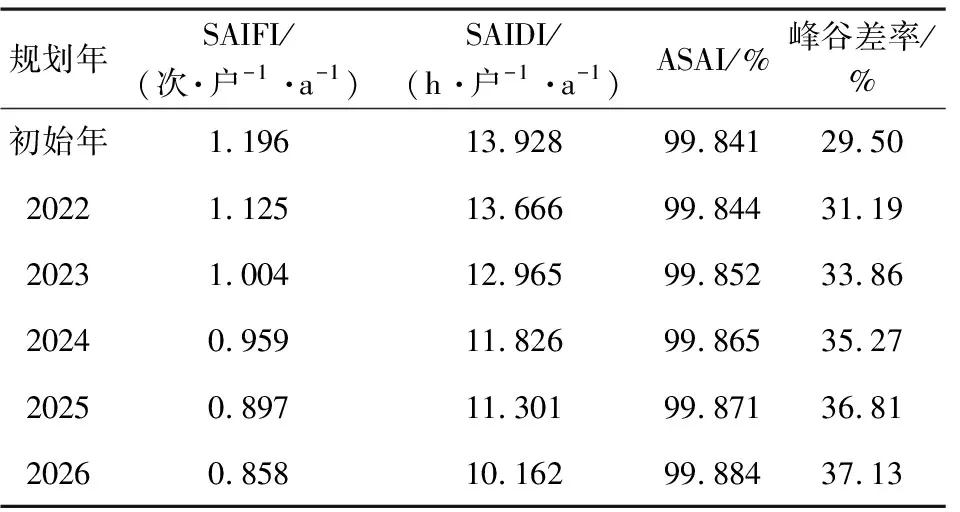
表6 传统规划后系统的可靠性与峰谷差率

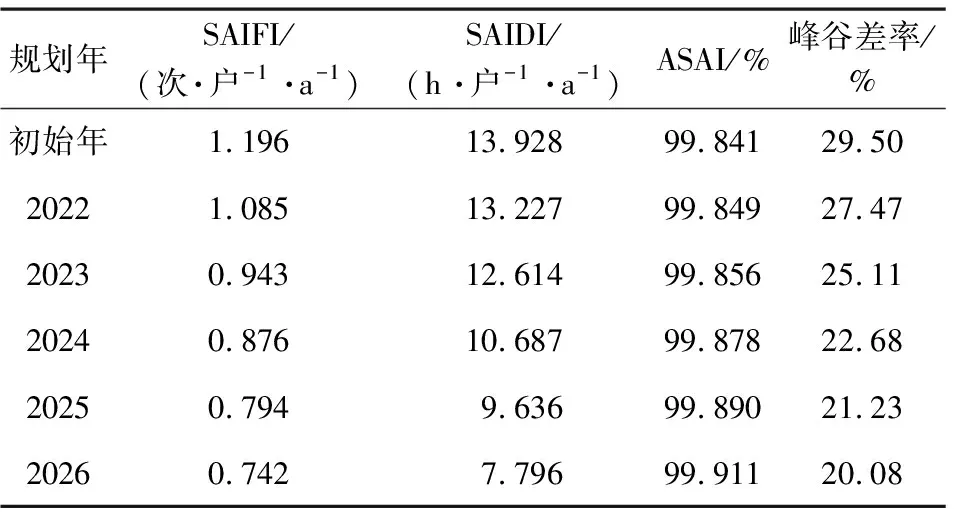
表7 联合规划后系统的可靠性与峰谷差率

由表6、表7可知,无论是进行传统规划还是联合规划后,配电网的SAIFI、SAIDI指标都随着线路的扩容和储能配置容量增大而不断下降,ASAI则不断提升,说明了系统的可靠性在不断提高。然而,仅进行线路扩容的传统规划的可靠性提升水平低于联合规划,且联合规划后系统的峰谷差率明显有所降低,峰谷差变小,而传统规划并不能保证这一点。

另外,考虑到所建模型将光伏消纳的环境收益耦合到了目标函数中,故对比了联合规划前后各个规划阶段下的光伏消纳率,计算方法如式(30)所示,计算结果如表8所示。

(30)

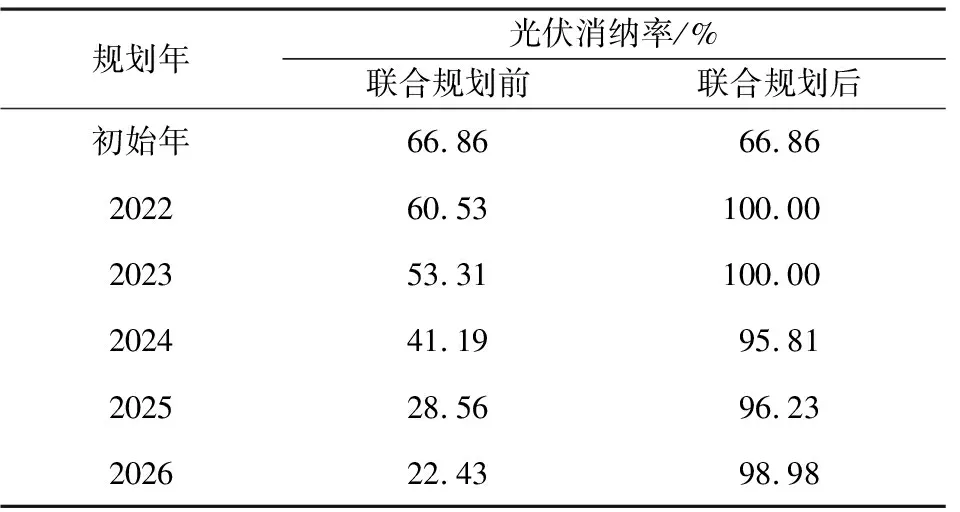
表8 联合规划前后系统的光伏消纳率对比

式中,ηPV为光伏渗透率。

显然,随着光伏的不断接入,未进行联合规划时配电网对光伏的消纳率将逐步下降;但经过线路的扩容和储能系统的优化配置,配电网的光伏消纳率不仅没有降低,反而有大幅提升,甚至能够保证超过95%,从而证明了所提联合规划在促进配电网对分布式光伏的消纳方面效果十分显著。

因此,在负荷的不断发展和光伏的陆续接入下,通过储能配置与线路扩容的联合规划,在部分节点配置一定容量的储能系统,并对部分线路进行扩容操作,有助于实现配电网的经济可靠运行。

5 结 论

上面综合考虑了光伏安装面积限制、配电网运行约束、多阶段规划连续性约束等,以规划成本最低为目标,建立含分布式光伏的配电网储能配置与线路扩容多阶段联合规划模型;同时通过相角松弛和二阶锥松弛凸化潮流约束,使用大M法凸化储能系统充放电功率约束,降低了原始非凸非线性动态规划模型的求解难度。实际算例表明,协同规划后,配电网运行指标如光伏消纳率和配电网可靠性都有显著提升,验证了所提分布式储能和线路容量联合规划方法的有效性。