小学数学“大概念”提炼及教学策略
2024-01-10高峰龄
高峰龄
【摘 要】大概念具有核心性、迁移性、生长性,指向素养目标,能够体现统领作用、知识体系建构和知识能力迁移。运用概括共通特征、发现本质属性、构建方法体系等策略能够提炼大概念。教师要基于大概念,设计大单元整体教学,更多指向学生的“学”,并制订进阶发展目标,设计单元内容,构建表现性评价体系,从而提升课堂教学效率,促进学生核心素养的发展。
【关键词】大概念 概念特征 概念提炼 教学策略 小学数学
提出“大概念”,旨在凸显其统领功能,体现迁移价值,提升学生的思维能力和学科素养,使其学会数学学习。
一、明晰大概念的特征
大概念不是一個具体概念或问题的表述,而是指向素养目标,体现统领作用、知识体系建构和知识能力迁移的核心观念,通常以概念、主题、论题、原理、方法等形式呈现,具有核心性、迁移性、生长性等本质属性。
核心性。位于某一知识体系整体结构的核心位置,能凝聚数学思想方法,统领该内容的学习。通过有限数量的大概念相互联结,形成知识内容、方法体系的立体结构,促进“四基”“四能”发展,提升学生的核心素养。大概念的核心性还体现在它是知识技能与核心素养的中介。在大概念统领下,学生立足结构化学习过程,能够更好地统整知识体系。新课标提出以“三会”构成数学课程,培养学生的核心素养,集中体现数学课程的育人价值。通过大概念将核心素养要求整体联系起来,体现其整体性、一致性和阶段性,显现出核心价值。
迁移性。大概念联结学校教育与现实生活,将对大概念的理解迁移到解决真实情境问题,能够培养学生在学习过程中的迁移能力,形成认知结构和核心素养。如学生经历长度测量的过程,理解制订标准单位以及统一单位的意义,从计量单位认知的角度提出大概念“长度单位及其个数的累加”,将其迁移到现实情境中,经历解决真实问题的过程,发挥大概念的迁移作用,选择或创造合适单位,运用估测的方法,对身边的事物进行测量,从而发展量感。
生长性。大概念之“大”,随着知识的丰富、认知的深入,会不断生长,进而提炼出统筹面更为广泛的核心概念,使其更具统领、迁移意义。如在“数与运算”主题中,教师可提炼大概念“计数单位的意义及个数累加”;在“图形认识与测量”主题中,提炼大概念“计量单位的意义及个数累加”,通过整合、生长,可形成更具统领价值的大概念“统一单位的意义及运用”。
二、提炼大概念的策略
大概念是抽象的,但又是具化的,其构建要经历“具体—抽象—具体”的过程。抽象大概念时需反思:提炼的大概念是否能统领知识体系,即所提炼的大概念能不能解释这一类现象,还能不能找到更上位的大概念,提炼的大概念能不能迁移解决真实情境问题等。
(一)把握知识结构脉络,概括共通特征,提炼大概念
大概念统领知识形成、发展、应用过程。在揭示知识结构脉络中的相通之处时,教师就可以提炼出大概念。以大概念指导教学实践,可以培养学生主动运用大概念迁移解决新问题的能力。
例如,在整数学习中,从十以内数的认识开始,逐步学习百以内数、千以内数、万以内数以及更大的数,对计数单位的理解是整个知识脉络的核心。教学从一个一个数走向十个一是一个十,十个十是一个百……学生以对计数单位的理解发展位值观念,相同的数字在不同的数位表示不同的意义,经历计数单位累加的过程。
又如,小数的认识,把1平均分成10份,形成计数单位“十分之一”,再不断地分,就有了百分之一、千分之一的计算单位。让学生经历计数单位细分的过程,明晰小数意义。
再如,整数、小数在分与合的思想下,形成整体,进而迁移计数单位概念。在度量不是整个数的物体时,学生可以用分数单位进行度量,累加相同的分数单位得到不同的分数。
从“数的认识”开始,教师把握整数、小数、分数意义的共通之处,提炼大概念“计数单位的意义”统领学习,在一致性结构框架下,迁移“计数单位的意义”,概括与数的运算本质相通的关键因素,围绕大概念“计数单位及个数的运算”进行数运算的教学。
(二)理解问题解决本源,发现本质属性,提炼大概念
运用知识的本质解决问题,把本质属性抽象为大概念。如“图形的测量”,从用非标准单位测量开始,体验统一度量单位的意义。学生运用测量工具进行度量一维图形长度、二维图形面积、三维图形体积时,均可将其转化为度量单位累加。由此,教师通过发现本质,提炼出大概念“度量单位意义及个数累加”。
(三)指向素养表现培育,构建方法体系,提炼大概念
学生在真实情境中运用数学眼光、数学思维、数学语言,离不开学习方法和习得路径,由此可以提炼出大概念。
如通过“观察—猜想—验证—结论—运用”的方法进行规律探索或新知学习,学生经历多次类似的探究过程,积累活动经验,形成初步模型意识,并能在以后的探究活动中主动运用,促进探究方法的迁移。由此,教师可以把这样的数学学习方法提炼为大概念。
三、基于大概念的教学
基于大概念的教学,可以理解为“以大单元为单位的整体结构型教学”。大单元之“大”体现在大概念视角下建构内容体系,初始阶段可以依托大概念设计由少量课时构建的“大单元”,进而随着大概念的聚合,大单元内容也随之丰富,逐步显现数学知识结构体系,还可以打破单一学科的壁垒,在不同学科之间提炼相通的大概念,并以此构建跨学科大单元。大单元并不一定限于集中讲授的课时教学,更多体现在不同学段在相通大概念统领下的内容结构。
大单元教学更多的指向学生的“学”,通过大概念、大问题、大任务组织单元教学,以“学”的实际情况展开学习活动,提升学生素养。
大单元教学的特点,其一是在单元知识结构体系中,体现联系与发展;其二是在习得过程中,注重迁移,在真实情境中,运用思想方法建构方法体系,建立学校教育与现实生活的桥梁,发展学生的关键能力,提升其素养。
从大概念视角梳理小学阶段的教学内容,找到关联,理解相通本质,形成结构化知识体系,构建大单元。大单元教学实施首先在分析课标、教材、学情的基础上,提炼大概念,设计单元进阶发展目标,制订单元学业质量标准,再创设真实情境,进行课时规划,运用大概念迁移,设计课时教学。
对于一线教师而言,重新打破现有教材编排体系构建新的大单元,有一定困难。我们可以在大概念统领下,基于内容体系结构特点,以现有教材自然单元为基础,整合、分解、调整相关内容形成大单元。
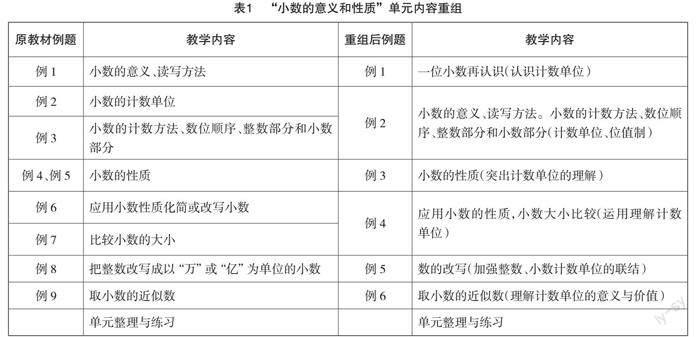
以下以苏教版数学五年级上册“小数的意义和性质”自然单元为例,谈大概念教学策略。
(一)厘清自然单元的内容结构
学生已学过“多位数的认识”“分数和小数的初步认识”,后续将学习“小数运算”“分数的意义和性质”等知识。本单元教材有9个例题,共教学8课时。例题1用多种形式表示长度,建立分数和小数的关联,初步教学百分之几的分数可以写成两位小数,千分之几的分数可以写成三位小数,以及两、三位小数的写法和读法。例题2学习计数单位、数位顺序、位值制。例题4与例题5通过具体量的比较发现小数性质,运用推理思想帮助学生理解小数性质,在比较归纳中发现性质,形成规律性语言。例题7通过计数单位理解大小比较和数的改写及取近似数的内容。
(二)大概念引领的单元目标及内容再构
在“数与运算”主题下,计数单位和位值制是学习的大概念。本单元的目标是在真实情境中,在大概念引领下,运用知识、学习方法的迁移,理解小数的意义和性质,并能够加以运用。
在此基础上,我们对教材自然单元进行重组。(见表1)学生在三年级学习时已有初步认识小数的经验,认识了一位小数,感悟到十分之几与一位小数的关系,并能在正方形图和数轴上正确找到相应的一位小数。本单元从一位小数的再认识入手,发现把计数单位“1”再平均分成10份,可以得到新的计数单位,也就是十分之一(0.1),以大概念“计数单位和位值制”为核心,联系真实情境进一步理解一位小数的意义。例题2运用类比的方法,将一位小数学习的方法迁移到多位小数的认识中,构建整数、小数数位顺序。从例题3开始,教师抓住计数单位,结合真实情境,引导学生学习小数性质、大小比较以及数的改写等内容,缩短单元内容教学课时,增加主题学习内容,如小数在生活中的运用,拓展到货币、度量等。经过重新设计,单元大概念更加明晰。学习过程中,为发挥知识与方法的迁移作用,减少教学课时数,教师由此开展实践活动。
(三)基于大概念的学习评价设计
大单元设计,还需有相应的评价方案。如“小数的意义和性质”教学内容经过重组后,教师要制订大概念统领下的评价设计。如“一位小数再认识”,设计三个层次的表现性评价。一星:会读写一位小数,了解计数单位“十分之一”;二星:能在生活情境中说清一位小数的意义,理解计数单位;三星:理解十进制整数、小数的关系,能用计数单位解释现实生活情境。
大概念教学,旨在建立结构关联,培育统整性思维并能运用解决问题,在真实情境中发挥知识、方法的迁移作用,学会数学的学习,发展能力、提升素养。
注:本文系江蘇省中小学教学研究第十四期重点自筹课题“基于扬州古运河文化的小学生项目化学习的研究”(课题编号:2021JY14-ZB51)的阶段性研究成果之一。
