多策略融合的多目标萤火虫算法

黄建平, 陈 谣,邢文来, 康 平, 赵 嘉

(南昌工程学院信息工程学院, 330099,南昌)

0 引言

近年来,人工智能技术得到了研究者们越来越多的关注,并取得了一系列重要突破。人工智能技术的发展正在慢慢改变着我们生活。深度学习技术可通过构建神经网络实现对复杂数据的分析和计算,从而实现高效的数据预测和决策。程鹏宇等[1]提出一种双向多尺度跳跃的短时温度预测模型应用于天气预测。群智能算法则是一种在自然界生物群体所表现出来的智能现象启发下提出的智能方法,具有自组织、自学习、自适应和内在并行性等特征,实现更加高效的信息处理和优化。张曦等[2]提出一种随机学习萤火虫算法优化的模糊软子空间聚类算法,使群智能技术和数据挖掘技术相结合,提高了聚类算法的性能。由此可见,人工智能已经成为当今科技领域最为热门的话题之一。随着计算机性能、存储容量和数据可用性的提高,人工智能可以处理和分析比以往任何时候都要大得多的数据集。其中,多目标优化问题(Multi-objective Optimization Problem, MOP)[3]出现在生活中的方方面面,而多目标问题的解决对于多种领域和应用非常重要和关键,例如在工业制造、环境保护、资源配置、城市规划等方面均存在大量的多目标问题。

多目标问题是指需要在多个目标之间进行权衡和选择的一类优化问题,即存在多个可能的解决方案,对其中一个子目标进行优化,可能会引起其他目标性能的降低,因此只能对多个目标进行折中处理,得到一组由非支配解组成的Pareto最优解[4]。传统的数学优化方法常常因为无法构造精确的数学公式而难以求解此类问题[5]。为了解决该问题,一种受生物启发求解MOP问题的算法——多目标进化算法(Multi-objective Evolutionary Algorithms,MOEAs)[6]应运而生,该类方法被认为是解决MOP问题的有效方法,并在各个领域获得广泛应用。

Yang[7]受自然界中萤火虫发光传递信息行为的启发,提出了萤火虫算法(Fireflyalgorithm,FA),该算法具有操作简单、参数少、收敛速度快及性能出色等特点,但也有易陷入局部最优、过早收敛等缺陷。为了提升FA的算法性能,诸多学者基于标准的FA做出改进。赵嘉等[8]提出一种深度学习萤火虫算法(Firefly Algorithm with Deep Learning,DLFA),该算法将最优萤火虫引入深度学习策略,采用随机吸引模型代替全吸引模型以防止萤火虫在移动过程中出现震荡,兼顾探索和开采平衡。赵嘉等[9]提出一种自主学习萤火虫算法(firefly algorithm based on self-learning, SLFA),该算法将粒子种群按适应度划分为自主学习粒子和普通粒子,在面临多峰优化问题时可有效地提升算法的寻优精度和多极值空间的探索能力。贺朝等[10]提出一种多策略集成萤火虫算法,该算法引入基于注意力机制的惯性权重结合邻域搜索策略修改了萤火虫的移动公式,优化了萤火虫在前期的勘探能力和后期的局部探索能力。鉴于FA的特性和优势,Yang[11]对标准FA进行了拓展,提出了多目标萤火虫算法(Multi-Objective Firefly Algorithm, MOFA)。MOFA算法中,笔者对萤火虫的移动公式进行了改进,萤火虫的移动依赖当前的Pareto最优解,使得算法的搜寻范围小,容易陷入局部最优,且算法在收敛性和分布性上效果均有所欠缺。针对此缺陷,LV等[12]提出了一种基于补偿因子与精英学习的多目标萤火虫算法(multi-objective firefly algorithm based on compensation factor and elite learning, CFMOFA),该算法引入补偿因子改进萤火虫的学习公式提高萤火虫全局寻优能力,采用精英个体学习扩大萤火虫的探索范围,提高了Pareto最优解集的多样性和准确性。赵嘉等[13]提出一种基于最大最小策略和非均匀变异的萤火虫算法(heterogeneous variation firefly algorithm with-maximinstrategy,HVFA-M),该算法引入Maximin策略添加改进学习策略提高算法的勘探能力和结合非均匀变异算子提高算法的寻优精度。

上述提到的算法虽然在一定程度上提升算法的性能,但是在收敛到真实的Pareto最优解的能力和解集覆盖域等方面仍存在不足。鉴于此,本文提出了多策略融合的多目标萤火虫算法(Multi-objective firefly algorithm based on multi-strategy fusion,MOFA-MSF)。MOFA-MSF具有如下特点:1)引入随机化与均匀化相结合的方法初始化种群,以此生成均匀分布的初始种群;2)设置外部档案,在外部档案中选择精英解来引导萤火虫移动,并在搜索过程中,根据当前外部档案中解的数量采用不同的方式选择精英解;3)引入变异算子和莱维飞行,使算法能够以较快的速度收敛的同时避免陷入局部最优;4)使用拥挤距离机制筛选精英解,以获得均匀分布的Pareto前沿。以上多种策略作用在算法的不同阶段,提升了MOFA各方面的性能。

1 多目标萤火虫算法

萤火虫算法是Yang根据萤火虫利用发光来传递信息的生物特性,提出的一种新的多目标优化算法。其核心思想是:亮度低的萤火虫受亮度强的萤火虫吸引,并向其靠近完成位置迭代,而亮度高的萤火虫不受任何萤火虫吸引,进行随机移动。

萤火虫i对萤火虫j的吸引力定义为:

(1)

式中,β0表示萤火虫的最大吸引力,通常取β0=1;γ表示光吸收系数,一般取γ∈[0.01,100];rij为萤火虫i到萤火虫j的欧氏距离,计算公式为:

(2)

若萤火虫j的亮度低于萤火虫i的亮度,萤火虫j会向着萤火虫i移动,其位置更新公式为:

xj(t+1)=xj(t)+βij(rij)(xi(t)-xj(t))+αε

(3)

式中,t是算法当前的迭代次数,xi为萤火虫i在搜索空间中的位置,α是步长系数,一般取α∈[0,1]。ε是服从正态分布、均匀分布或者其他分布的随机数向量。

若不存在亮度高于萤火虫j的个体,即萤火虫j不被任何萤火虫吸引,其位置更新公式为:

xj(t+1)=g*+αε

(4)

式中,g*是以随机加权和的方式将多目标函数转换为单目标函数得到的当前最优解。对于求解最小值问题,若不存在萤火虫u使得ψ(xu)<ψ(xv),则当前的最优解g*即为萤火虫v。ψ(xv)定义为:

(5)

式中,E表示目标函数的个数,we为(0,1)之间的随机数。

2 MOFA-MSF算法

2.1 种群初始化策略

大部分多目标萤火虫算法采用随机初始化的方式生成初始种群,随机初始化方式的缺点在于仅考虑了生成种群的随机性而没有考虑初始种群在决策空间中的分布问题。针对这一问题,引入均匀化与随机化相结合的初始化方法[14]产生初始种群。该方法有如下优势:1)保持了选取子区间和在区间中生成位置的随机性;2)使初始种群均匀分布在决策空间中。以这种方式获得均匀的分布的初始种群,为MOFA-MSF算法的全局搜索奠定了良好的开端。该初始化方法的流程为:

输入:种群数量N,决策向量的维数D,每个决策变量xd(d∈[1:D])的范围[ad,bd]。

输出:初始化种群。

步骤1:d= 1,j= 1。d和j分别表示当前遍历的维度和萤火虫。

步骤2:当d<=D时,重复步骤3～步骤9。

步骤3:对决策变量xd的范围区间[ad,bd]进行划分,计算ωd=(bd-ad)/N。

步骤4:得到θd={[ad,ad+ωd],[ad+ωd,ad+2ωd],…,[ad+(N-1)ωd,bd]}。

步骤5:当j<=N时,重复步骤6～步骤8。

步骤7:从集合θd中删除步骤6所选中的区间。

步骤8:j=j+1。

步骤9:d=d+1。

步骤10:输出初始种群{x1,x2,…,xN-1,xN}。

2.2 随机扰动策略

多目标萤火虫算法的步长依赖于步长系数α,且α会随着迭代次数的增加而减小,这使得萤火虫之间的步长差别越来越小。这种情况不利于多目标萤火虫算法求解具有复杂Pareto前沿的MOP问题。因此,本文引入Lévy flight随机扰动代替原有的随机步长,以平衡算法的局部搜索和全局勘探能力,提升算法求解复杂MOP问题的能力。

莱维飞行(Lévy flight)[15]是法国数学家Lévy提出的一类非高斯随机过程,是一种具有概率分布步长的随机游走,是随机游走模型中最好的策略之一。

莱维飞行的随机步长s的计算公式为:

(6)

式中,v和μ均为服从正态分布的随机数,它们的定义为:

(7)

上式中,σv和σμ的计算公式为:

(8)

式中,通常取φ(1,3),本文取φ=1.5;Γ为标准的Gamma函数。

2.3 变异算子

萤火虫之间的个体差异会随着算法的进行和种群的不断更新变得越来越小,这可能会使萤火虫之间出现严重的聚集现象。为了避免种群陷入局部最优,本文引入变异算子[16],萤火虫k在每次进行位置更新之后,按照变异概率pm随机对萤火虫k的一个分量进行扰动,pm的计算方式为:

(9)

式中,t是当前迭代的次数,maxT为最大迭代次数。

若随机选中的是第j维度分量,萤火虫k的变异公式为:

(10)

式中,xk(j)为萤火虫k第j维度的值,lj和uj分别代表萤火虫k在第j维度上的下限和上限,pm表示变异的概率,rand(1)表示0到1之间的随机数。下限lj和上限uj的计算方式为:

(11)

式中,u和l分别表示萤火虫在解空间内的上界和下界。

算法前期,萤火虫的变异概率和扰动幅度较大,算子能够充分发挥算法的全局搜索能力,使种群具有更好的分布性。算法后期,萤火虫变异的概率变小且扰动的幅度也随之减少,算子更加注重局部搜索,使得产生后的解有着更大的概率靠近真实的Pareto前沿,维护了种群的收敛性。

2.4 档案精英解引导萤火虫移动

MOFA-MSF算法迭代过程中,外部档案始终不为空集,所以,当萤火虫i与j因互相吸引而更新位置时,算法将从档案中选取一个精英解A*引导萤火虫进行移动。区别于MOFA算法,萤火虫i和萤火虫j之间相互移动存在2种情况:

1)当萤火虫i和萤火虫j互不吸引,彼此非劣时,i和j都将在精英解A*的引导下进行位置更新,移动公式[11]为:

(12)

2)若萤火虫i和萤火虫j之间存在吸引关系,假设萤火虫i吸引j,那么萤火虫j将同时向着精英解A*和萤火虫i移动,移动公式为:

(13)

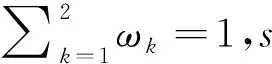
区别于随机选取,本文在选取精英解A*时,根据外部档案中解的数量采取不同的选择方式。大致思想为:1)若外部档案未满,则从外部档案中随机选取解作为精英解;2)若外部档案已满,优先选取外部档案中拥挤度大的解作为精英解,例如,对外部档案中的解由拥挤度从大到小排序,从档案的前50%的个体中选取精英解。在上述选取的精英解引导下,本文算法会优先搜索拥挤距离大的区域,能够在一定程度上使得获得的解集分布更加均匀且加快种群的收敛速度。

2.5 拥挤距离策略维护外部档案

多目标萤火虫算法通常采用容量有限的外部档案来存储迭代过程中获得的非劣解,当非劣解数量超出档案规模时,要对档案进行裁剪来维持档案中解的多样性。为了获得均匀分布的Pareto前沿,提高MOFA-MSF算法的性能,本文引入拥挤距离策略。

拥挤距离策略[17]是多目标优化算法中常用的一种选择压制性策略,其主要思想是在选择解的过程中不但要考虑目标值函数,还要考虑解的拥挤度,从而保证选择的解具有良好的多样性和分布性。拥挤距离策略的优势在于,其实现简单,易与各种优化算法相结合。

以最小化问题为例,对于萤火虫j,其拥挤距离distj的计算公式为:

(14)

拥挤距离大的解,周围的解越稀疏,拥挤距离小的解,周围的解越密集。在外部档案超出规模时,通过拥挤距离对非支配解排序,保留拥挤距离大的解,以此来获得均匀分布的Pareto解集。

2.6 算法流程

结合上述多种策略,给出MOFA-MSF算法的流程:

输入:种群规模N,外部档案Arc的规模ArcNum,最大迭代次数maxT,萤火虫的最大吸引力β0,光吸收系数γ,步长系数α。

输出:Pareto最优解集。

步骤1:利用随机化均匀化初始化策略生成规模为N的初始种群,迭代次数t=0。

步骤2:计算每只萤火虫的适应度值。

步骤3:对初始种群进行快速非支配排序,筛选得到初始非支配解集并将前ArcNum个个体存储在外部档案Arc中。

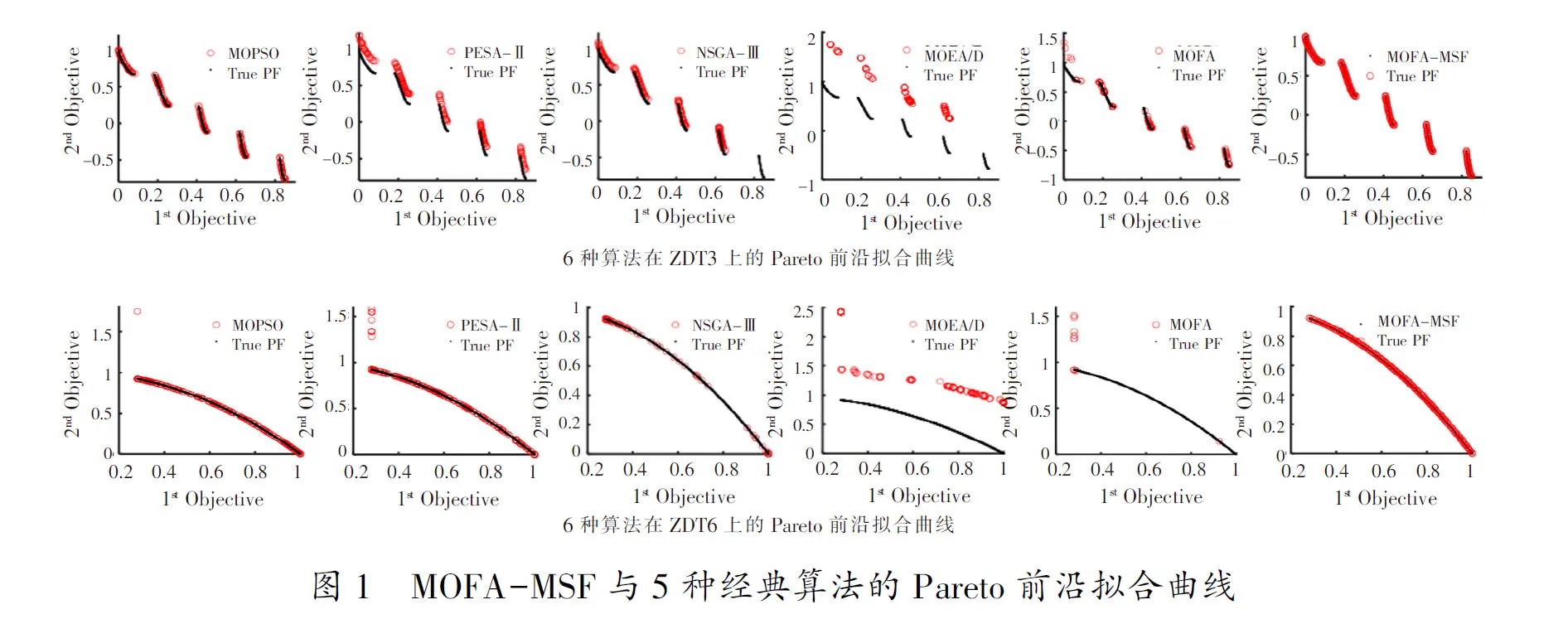
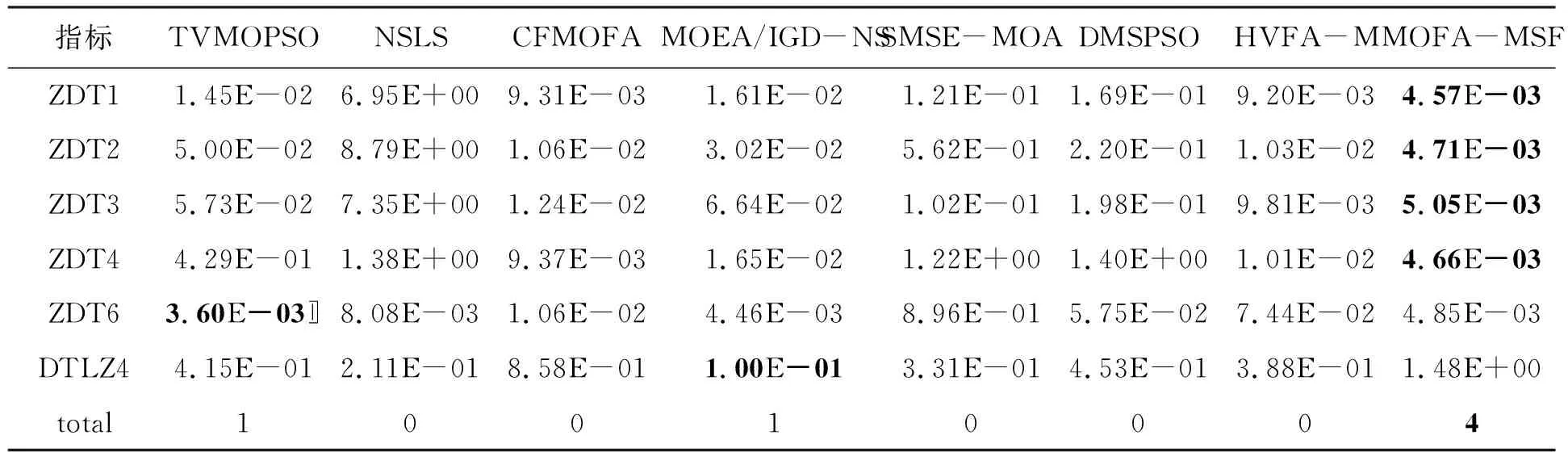
步骤4:当t

步骤5:遍历萤火虫,重复步骤6～步骤8。

步骤6:根据档案中解的数量用不同的方式从外部档案中挑选出精英解A*。

步骤7:判断萤火虫i和萤火虫j之间是否存在吸引关系。若是,被吸引萤火虫按照公式(13)更新位置,否则,2只萤火虫均按照公式(12)更新位置。

步骤8:采用变异算子对更新后的萤火虫进行变异,若变异后的位置优于变异前,则进行位置更新,否则,不进行任何操作。

步骤9:更新种群的适应度值。

步骤10:更新外部档案Arc,若外部档案中解的数量超出规模,利用拥挤距离策略删除多余解。

步骤11:t=t+1。

步骤12:输出Pareto最优解集。

3 实验与结果

为验证MOFA-MSF的性能,整个实验包括2个部分:1)MOFA-MSF与经典多目标优化算法对比;2)MOFA-MSF与新近多目标优化算法对比。

3.1 与经典多目标优化算法对比

本节将MOFA-MSF与5种不同的经典多目标优化算法:MOPSO[18],PESA-I[19],MOEA/D[20],NSGA-III[21]和MOFA[11]在7个测试函数上进行对比。MOPSO、NSGA-III、MOFA、MOEA/D和PESA-II的实验结果均取自文献[13]。本文采用反转世代距离(Inverted GenerationalDistance,IGD)[22]评判算法的优劣。为确保算法比较的公平性,MOFA-MSF和这5种经典算法的参数设置如表1所示,和其他算法的参数一样,本文设置最大迭代次数maxT为300,种群大小为N为50,外部档案大小ArcNum设置为200。为克服随机因素的干扰,每个算法在每个函数上均独立运行30次,取算法独立运行30次的平均值作为评价指标。

表1 各经典算法的参数设置

表2列出了MOFA-MSF与其他5种经典算法在7个测试函数上的IGD的标准差(std)和均值(mean)及每个算法在所有测试函数上获得的最优值的总数(total),表2中加黑的数据代表这6种算法在同一个测试函数上的最优值。从表2可知,MOFA-MSF算法在实验中,除Vinnent1之外的其他测试函数均取得最优值,说明MOFA-MSF的收敛性和勘探能力相较于这些经典优化算法有了较大提升。在测试函数Viennet1下,PESA-II算法在IGD的均值上优于其他几种算法,但MOFA-MSF在数量级上与其相同且系数差别很小,与此同时MOFA-MSF具有更小的IGD标准差,说明在这个测试函数上二者相差很小。综上所述,相较于这几种经典优化算法,MOFA-MSF算法在收敛性和多样性方面体现了较强的优势。

表2 MOFA-MSF与经典优化算法在IGD上的对比结果

表3给出了在IGD上基于Friedman校验的各多目标优化算法结果的秩平均值和平均排名,可以看出MOFA-MSF排名第1,随后分别是MOFA、PESA-II、NSGA-III、MOPSO,其中NSGA-III和MOPSO拥有相同的秩,排名并列第4,最差的是MOEA/D。表3的结果表明,MOFA-MSF相较于其他5种经典算法,求解精度更高,收敛性更好,综合性能更强。

表3 各个算法在IGD上基于Friedman校验的平均排名

为了更加直观地体现MOFA-MSF的优势,图1列出了MOFA-MSF在2个测试函数上与5种经典算法上的Pareto前沿图,其中黑色实线表示真实Pareto前沿,红色圆圈表示算法所求得的Pareto前沿。可以看出MOFA-MSF相较于经典算法在均匀性分布性上均有较强的优势。

3.2 与新近多目标优化算法对比

为了进一步验证MOFA-MSF的性能表现,本节将MOFA-MSF与7种新近的多目标优化算法:HVFA-M[13]、TVMOPSO[23]、NSLS[24]、CFMOFA[12]、MOEA/IGD-NS[25]、SMSE-MOA[26]和DMSPSO[27]进行对比。表4给出了MOFA-MSF与这7种新近算法的相关参数。

表4 MOFA-MSF与7种新近算法的参数设置

为确保实验的公平性,除TVMOPSO、SMSE-MOA和DMSPSO的迭代次数保留原有的设置外,其余算法在2目标问题上迭代次数均设置为250,3目标问题设置为500。外部档案大小ArcNum均设置为100。本算法的其余参数设置与3.2节相同。为克服随机因素的干扰,每个算法在每个函数上均独立运行30次,取IGD平均值(Mean IGD)作为评价指标。

表5列出了MOFA-MSF与这7种算法的对比结果,表中最后一行的total表示各个算法获得最优值的次数,加黑的数据代表这8种算法在同一个测试函数上的最优值。从表5知,MOFA-MSF算法在6个测试函数上共取得4次最优。TVMOPSO和MOEA/IGD-NS分别在ZDT6和DTLZ4测试函数上各取得一次最优,其余算法未取得最优。表6是MOFA-MSF与这7种新近算法基于Friedman校验的结果的秩平均值和平均排名,可以看出MOFA-MSF排名第一,随后依次是HVFA-M、MOEA/IGD-NS、CFMOFA、TVMOPSO、SMSE-MOA、NSLS,最差的是DMSPSO。综上所述,MOFA-MSF算法相较于这些新近多目标优化算法,依旧表现出较强的性能,且在收敛性和多样性仍具有较强的优势。

表5 MOFA-MSF与7种新近多目标优化算法在IGD上的对比结果

表6 各个算法在IGD上基于Friedman校验的平均排名

经过两轮的对比实验可知,MOFA-MSF是一种有效且可行的多目标优化算法,在收敛性、分布性和勘探能力方面均表现出较强的优势。原因在于,MOFA-MSF针对MOFA算法的缺陷,使用随机化均匀化相结合的方法初始种群,再根据档案中解的数量采用不同方式选取精英解并利用该精英解引导萤火虫移动,引入变异算子提升算法的局部探索能力,在萤火虫移动公式中加入莱维飞行随机扰动代替原有随机步长,采用拥挤距离策略维护外部档案,以上多种策略融合在一定程度上优化了MOFA的收敛性差、分布性差和勘探能力弱等特点。

4 结论

针对MOFA所表现的问题,本文提出了多策略融合的多目标萤火虫算法。首先,利用均匀化与随机化相结合的初始化方法产生均匀分布的初始种群,为全局探索奠定了基础;采用档案精英配合莱维飞行随机扰动引导萤火虫的移动,在选择档案精英时,根据档案中解的数量,采用不同的方式选择精英解;引入变异算子,对进行过移动的萤火虫的分量进行一个扰动,提升了种群的局部探索能力;最后,采用拥挤距离机制对外部档案进行更新维护,以获得最接近真实Pareto前沿的均匀分布的最优解集。本文使用MOFA-MSF在7个测试函数上与5种经典优化算法进行对比、在6个测试函数上与7种新近算法进行对比。实验表明,MOFA-MSF在各个测试函数上均具有较为出色的性能。通过与这些经典算法和新近算法的对比,证实了本文多策略融合的有效性,提升了MOFA算法的性能。