环形天线结构点头模态的T-S 型模糊控制
2024-01-10马国亮马小飞徐明龙杜虎兵蒋丽丽
马国亮,马小飞,徐明龙,杜虎兵,蒋丽丽
(1.西安工业大学机电工程学院,陕西 西安 710021;2.中国空间技术研究院西安分院,陕西 西安 710100;3.西安交通大学复杂服役环境重大装备结构强度与寿命全国重点实验室,陕西 西安 710049;4.上海宇航系统工程研究所,上海 201109)
引言
环形天线是当今空间大口径卫星天线的主流形式,环形天线的口径从几米到上百米,美国诸多电子侦察卫星上的天线均采用了这种结构形式,中国也正在研究此类大口径天线。星载大型环形天线由于尺寸大和刚度小,呈现明显的低频振动特性,且因阻尼小而衰减缓慢,从而影响天线的工作品质[1]。在卫星地面振动控制试验时,消除重力的影响尤为重要[2]。因为在卫星发射前的地面试验中,重力作用使环形天线结构产生严重的静态变形,增加力学试验的难度,影响振动控制的准确性[3]。面对无法避免的重力因素,通过绳索悬吊航天器进行动力学试验具有结构简单可靠、附加刚度小的优点,若绳索的长度足够长,恒力稳定,可以实现航天器低重力甚至零重力模拟[4]。Fischer 等[5]设计的可折叠太阳翼展开机构采用被动式跟随方法进行低重力实验,恒力吊索的长度几乎不变,悬挂点不存在竖直方向的运动。杨巧龙等[6]为某航天器的太阳能帆板设计了一种悬吊装置,在重力卸载后具有运动跟随功能,完成了帆板的全部展开。对卫星环形天线结构悬吊后的振动特性研究表明,环形天线结构前两阶固有模态为“点头”模态和“摇头”模态。Luo 等[7]开发了一种单根吊索悬吊装置,吊起了与天线近似的环形柔性结构,实测得到了水平方向的“摇头”模态。郑宜生等[8]提出了一种多点负刚度磁弹簧悬吊装置,能够平衡环形柔性结构的重力,且在水平方向上,对结构只有很小的附加约束,使悬吊后的“摇头”频率接近无重力时的频率。然而,现有悬吊装置在振动特性方面还存在一些问题。比如单点悬吊装置的悬吊绳够长,但未实现环形结构竖直方向的“点头”模态;三点悬吊装置实现了双模态,但“点头”模态受到悬吊装置的干扰。现有文献也很少涉及深入研究环形结构模态解耦的问题[9]。
在环形天线结构悬吊后进行振动控制时,应用算法对反馈信号进行运算产生控制信号,驱动作动器完成作动,所以,控制算法是振动控制的核心。常用的控 制算法 有PD(Proportional Differential)控制、模糊控制、LMS(Least Mean Square)自适应控制,LQR(Linear Quadratic Regulator)控制、H∞鲁棒控制算法等[10-12]。PD 控制包含比例和微分控制环节,只有比例控制时,系统输出存在稳态误差,增加微分项,避免了被控量的超调现象。模糊控制一般采用二维Mamdani 型模糊逻辑规则库,包含模糊化与清晰化过程,鲁棒性和适应性较好。LMS 自适应控制即最小均方自适应滤波控制,具有与起始条件无关、计算复杂度低、均值无偏差收敛到Wiener 解等优点,适合建立复杂振动控制系统。但是对于环形天线结构,振动模态复杂,可能存在非线性,要求控制系统精确、可靠。而T-S 型模糊控制适合将非线性问题转化为分段线性问题,与Mamdani 型控制相比,不需要经过复杂的清晰化过程,直接输出状态量的线性函数,设计控制器[13]。T-S 型模糊控制的关键在于结构辨识和参数辨识,建立T-S 型模糊推理。
综上所述,环形天线结构频率低、形变大。当悬吊绳的长度有限时,结构能够实现小摆角振动,且结构的模态解耦,才能进行地面振动主动控制试验。本文以悬吊后环形天线结构的缩比模型为控制对象,以振动参数建立状态空间方程,确定T-S 型模糊控制规则,并研究T-S 型模糊振动控制的效果。
1 悬吊解耦及模态分析
由于实物环形天线的尺寸和质量太大,以一个缩比模型进行分析。缩比模型应遵循“频率与振型等效原则”,即固有频率和振型与实物接近[14]。为了降低装置的干扰作用,根据环形天线结构的构型和前两阶模态,独立设计“点头”方向悬吊装置,即环面侧放。在环面顶部节点处,绳索悬吊于外部结构,“点头”模态的振动方向与重力和悬吊的方向垂直,如图1 所示为两根绳索的悬吊装置。同时,根据主动控制原理,在柔性伸展臂根部设置MFC(Macro Fiber Composite)作动器,结合传感器和控制器构成主动控制系统。

图1 悬吊及控制示意图Fig.1 Suspension and control diagram
缩比模型的参数如表1 所示,环的质量为M2=0.35 kg,伸展臂的质量为M1=0.125 kg,节点处配重质量mi=0.070 kg,悬吊绳材质为凯夫拉纤维,与其他结构相比,悬吊绳的质量可忽略。
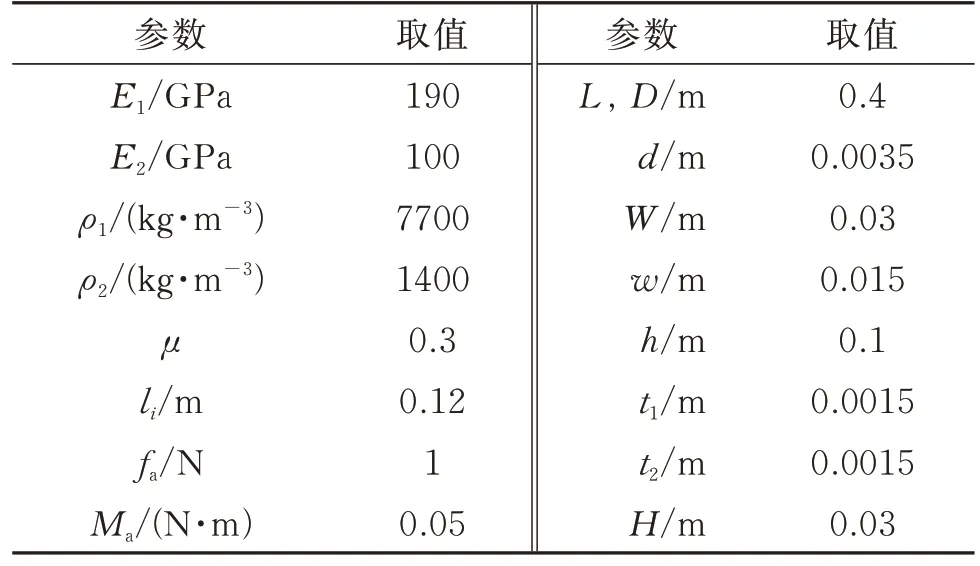
表1 缩比模型参数Tab.1 Scaled model parameters
采用有限元方法分析了缩比模型的固有频率和模态。应用MSC Patran 建立了包含30 个节点,8 个集中质量单元CONM2 和38 个杆单元CBAR 的三维模型,伸展臂的根部固定,应用Lanczos 方法求解振动特性,得到悬吊前后的前两阶固有模态和频率如图2 所示。

图2 前两阶模态Fig.2 The first two order modes
第一阶模态为环面的上下摆动,称之为“点头”模态,第二阶模态为环面的左右摆动,称之为“摇头”模态,“点头”模态和“摇头”模态的振动方向垂直,与卫星环形天线的前两阶模态近似,其他更复杂的高阶模态暂不考虑。当悬吊绳长为0.12 m 时,悬吊前后前两阶固有频率分别为1.44,1.74 Hz 和1.48,5.18 Hz,由于1.44 Hz≈1.48 Hz,1.74 Hz≠5.18 Hz,因此,环面侧向放置方式解决了“点头”模态解耦的问题,“摇头”模态不采用环面侧向的方式更好。
2 T-S 型振动控制分析
环形天线结构为多自由度系统,应用振动主动控制方法,多自由度系统的振动控制方程为:
式中Mn,Kn和Cn分别为质量、刚度和阻尼矩阵;xn为节点位移;Fe为外部激励力向量;Fa为控制力向量。当应用模糊控制算法对反馈信号进行模糊逻辑运算得到控制信号S时,控制力为:
式中fa为单位力;Fu表示模糊控制算法;x为反馈信号;ke,kec和ku为模糊控制参数。控制信号可以是电压或电流,具体由作动器的类型决定。一般情况下,模糊控制算法采用二维Mamdani 型规则对信号进行模糊化和清晰化运算,计算复杂度高,但对于线性控制系统,T-S 型模糊规则直接输出线性函数,极大地降低复杂度,便于分析和运算。
设结构低阶振动在一定范围内为线性微振动,线性时不变系统的状态空间模型为:
式中x(t)为系统的状态变量;u(t)为输入量;y(t)为输出量;e(t)为误差;A为系统矩阵;B为输入矩阵;C为输出矩阵;D为直接转移矩阵;K为增益矩阵。
对于缩比模型,当x为某测点的振动位移,并作为振动控制系统的反馈,状态变量为:
以此建立T-S 模糊控制,输出函数f(x1,x2)采用一阶T-S 模糊规 则:ifx1isA1andx2isA2,then(fx1,x2)=px1+qx2+r。其中,A1,A2为位移和速度的范围,p,q,r为待定系数,需要大量的输入-输出测试数据经过辨识得到。如果x1和x2的隶属度为ZR,则得到:
当输入量u(t)为反馈信号输入控制器时,只要状态空间模型的参数确定,T-S 模糊控制的规则为状态变量x('t):
然后,通过矩阵运算得到一阶T-S 模糊规则:
3 模型辨识和振动控制
3.1 系统辨识
根据上述分析,先建立无控制状态的振动测试,对输入-输出数据进行辨识,得到状态空间模型,以此确定T-S 型模糊规则。图3 为应用有限元分析的模态数据建立的正弦激励程序,稳态激励信号为0.03sin(ω1t),作用在环端部节点水平方向上,得到测点18 的稳态响应。
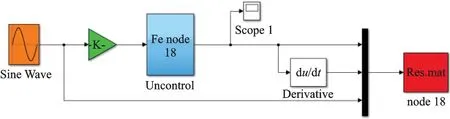
图3 振动测试Fig.3 Vibration test
测试后提取正弦激励,得到输出位移,瞬时速度信号,如图4 所示。由图4 可见振动位移和速度的取值范围 分别为[-0.0068,0.0068] m,[-0.062,0.062] m/s。然后,对输入输出数据进行系统辨识,分析状态空间模型。
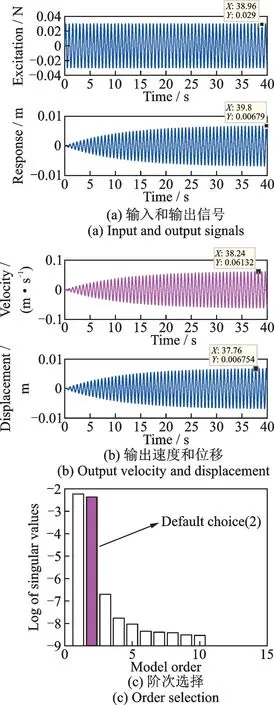
图4 振动响应和模型阶次Fig.4 Vibration response and model order
在状态空间阶次选择中,二阶是最优辨识结果,模拟输出数据相似度达到了95.66%,通过结构辨识得到二阶状态空间方程各个矩阵分别为:
因程序中未引入误差信号,因此误差e=0,得到下式:
代入式(8)数据后得到式(5)和(7)表示的T-S型模糊规则分别为:
然后根据上述T-S 型模糊规则分别建立模糊控制规则库,其中位移和速度的隶属度ZR 分别为[-0.007,0.007] m,[ -0.07,0.07] m/s。在选择隶属度函数曲线时,可以选择高斯型和三角型,如图5所示。模糊规则u对应的输出面为图5(a)和(b),可见模糊规则u对应的高斯型函数输出面为连续线性曲面,三角型函数输出面为分段的曲面,模糊规则y对应的输出面均为图5(c)所示线性曲面。
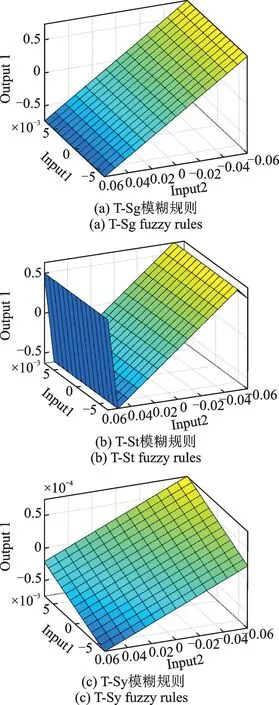
图5 T-S 模糊控制的规则Fig.5 T-S rules of fuzzy control
3.2 T-S 模糊控制
根据振动控制原理,应用MATLAB/Simulink对悬吊后的模型进行了控制仿真。仍以有限元模态分析的结果构造了质量、刚度和瑞利阻尼矩阵,根据状态空间方程建立振动控制程序如图6 框图所示,稳态激励信号为0.03sin(ω1t),作用在环端部节点水平方向上,非控制模块Uncontrol 输出响应,测得节点18 的位移,同时测量模块Measure 输出节点18 的位移,作为反馈信号输入到模糊控制算法。然后模糊控制算法经过运算产生控制信号输入到Actuator 模块,即控制模块将控制信号转换为力信号抑制振动。其中MFC 作动器在节点处的力和弯矩分别为fa=1V(t)和Ma=0.05V(t),V(t)为电压。图7 为三种T-S 模糊规则建立模糊控制后的位移响应抑制结果。
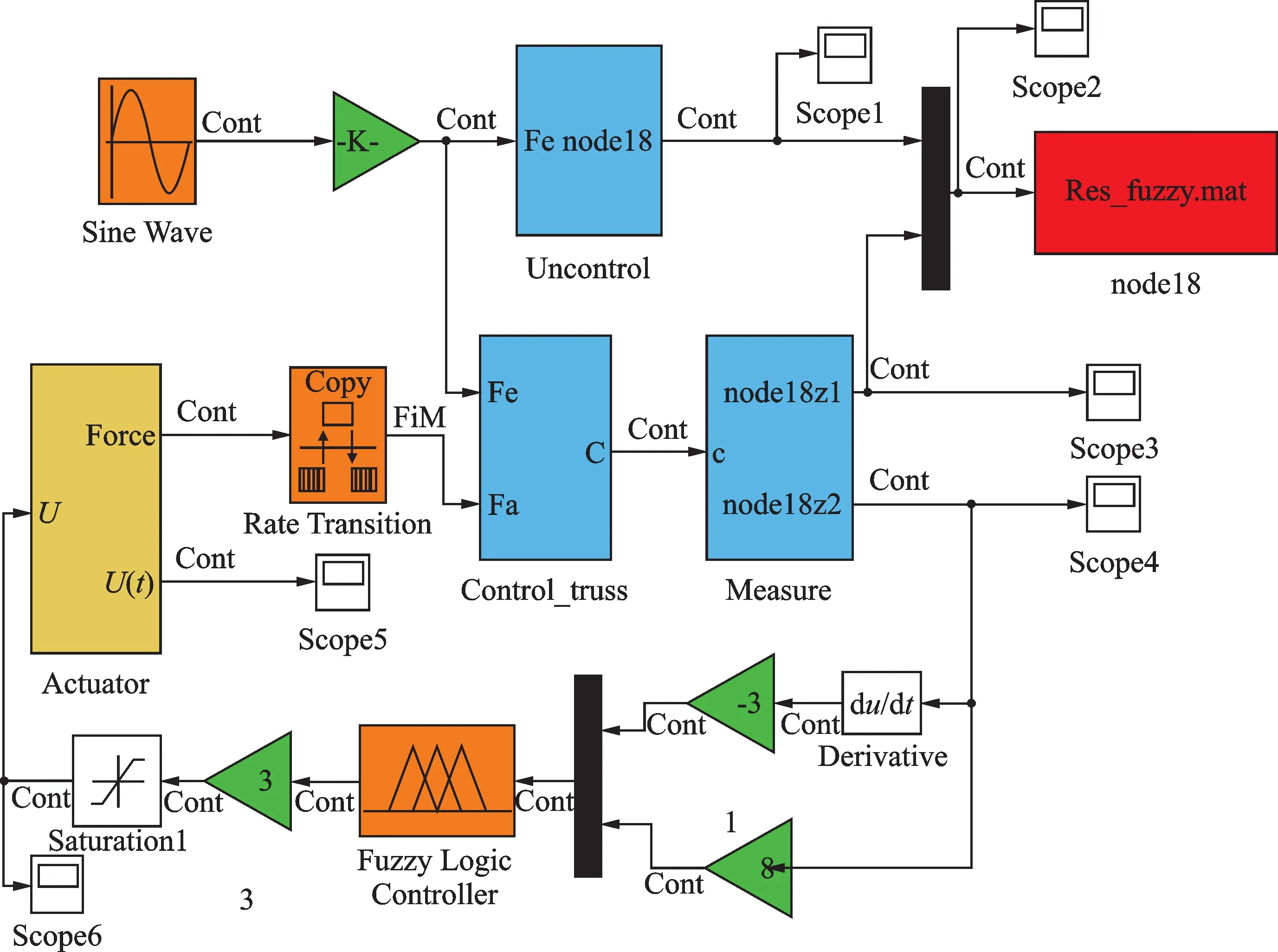
图6 振动控制程序Fig.6 Vibration control procedure

图7 振动控制结果Fig.7 Vibration control results
图7 和表2 为模糊控制的结果和参数,结果表明采用模糊规则u和gaussmf 型隶属度函数后,稳态振幅抑制率达到85% 以上,瞬态振动衰减率60% 以上。例如,控制前的位移为0.67×10-2m,但控制后的位移为0.085×10-2m,振幅抑制率为87.3%,其他模糊控制效果一般。

表2 振动控制结果Tab.2 Vibration control results
4 结论
本文通过悬吊解耦得到了环形天线结构一个缩比模型的“点头”模态,并研究了如何确定T-S 模糊控制的规则,最后进行了T-S 模糊振动控制,主要得到以下结论:
(1)悬吊解耦可以实现模态解耦,悬吊前后固有频率接近,且“点头”模态受到的影响较小。
(2)通过系统辨识得到状态空间模型,并确定T-S 型模糊控制的规则,通过仿真模拟,发现采用gaussmf 型隶属度函数可得到连续线性的输出面。
(3)建立模糊控制程序,对结构施加不同的激励,发现采用模糊规则u和gaussmf 型隶属度函数后,振动抑制效果显著,为后续环形天线实物的试验验证提供了技术支撑。
