浮式螺旋型垂直轴风机动力响应计算研究
2024-01-10邓万如刘利琴张立昌
邓万如,刘利琴,李 焱,张立昌
(天津大学水利工程仿真与安全国家重点实验室,天津 300350)
引言
随着海上风机逐渐向深海发展,浮式风机逐渐成为一个更经济的选择。基于旋转轴的方向,浮式风机可以分为水平轴风机与垂直轴风机两类。目前来看,水平轴风机具有较高的风能利用率和比较成熟的技术;垂直轴风机的主要优势在于受风多向性,安装维修成本较低,易于大型化等[1]。
螺旋型垂直轴风机可以看作基于直叶片垂直轴风机的变异优化,优点是可以提高风机的自启动性能并且降低转矩波动。Wang 等[2]基于CFD 方法分析了螺旋型风机的气动特性,并与传统的H 型风机进行对比,结果表明采用螺旋变异设计的风机可以减小气动力的波动。张珊珊[3]建立了螺旋型风机参数化三维模型,通过采用合理的设计参数,降低了叶片转矩波动并提高了平均动转矩水平。刘利琴等[4]分析了螺旋扭曲角、叶尖速比、弦长和桨距角等参数对螺旋型风机气动特性的影响,并给出了优化后的结构参数组合。
在复杂海洋环境下工作的兆瓦级浮式风机系统,会受到包括气动载荷、波浪载荷、重力载荷、惯性载荷等多种载荷的作用,这些载荷会对风机的动力响应特性以及疲劳特性产生影响,进而会威胁到风机的使用寿命。因此,研究浮式风机系统的动力响应对保障风机安全运行有着重要作用。目前,FAST,Bladed,HAWC2 等商业软件已被广泛应用于浮式风机动力响应数值计算。国内外学者也对浮式风机的动力响应开展了大量研究工作。刘格梁等[5]研究了浮式水平轴风机基础运动对风轮气动特性的影响,从入流角度方面分析了气动载荷变化的原因。肖昌水[6]基于若丹速度变分原理和一次近似建模理论推导了浮式水平轴风机刚-柔耦合多体动力学方程,并以OC4-DeepCWind 海上浮式风机系统为例计算分析了浮式基础、塔柱以及叶片的动力响应特性。Alkarem 等[7]研究了不同波浪谱形状参数以及多种波浪方向下水平轴浮式风机的动力响应。Cheng 等[8]选取随机波和湍流风工况,研究了叶片数量对浮式直叶片垂直轴风机动力响应的影响。
总体而言,虽然已有许多研究对浮式水平轴风机以及传统直叶片垂直轴风机的动力响应进行了分析,但目前对于螺旋型风机的研究主要集中于气动性能,并且研究对象主要为陆上螺旋型风机,对大型浮式螺旋型风机系统动力响应的计算研究非常少见。基于以上原因,本文对一种螺旋扭曲角为120°的三叶片5 MW 浮式螺旋型垂直轴风机进行研究,基于一种松耦合方法建立整机计算模型。编写数值求解程序,计算风浪联合作用下的风机动力响应。与直叶片风机进行对比,研究了螺旋扭曲角对气动转矩、浮式基础运动、塔柱变形以及叶片变形产生的影响。
1 风机模型
本文研究的浮式螺旋型风机系统如图1 所示。上部的风机结构参数主要参考了FloVAWT[9]风机模型,撑杆分别位于叶片的顶部、中部和底部,螺旋扭曲角设置为120°。其中螺旋扭曲角是在保证风轮高度、叶片弦长不变的情况下,将叶片沿着逆时针方向螺旋扭曲一定的角度,如图2 所示。风机的主要参数如表1 所示。下部结构包括浮式基础以及系泊系统,本研究选用OC4 半潜型浮式基础[10],三根系泊缆间隔120°均匀布置,浮式基础以及系泊系统的主要参数如表2 所示。
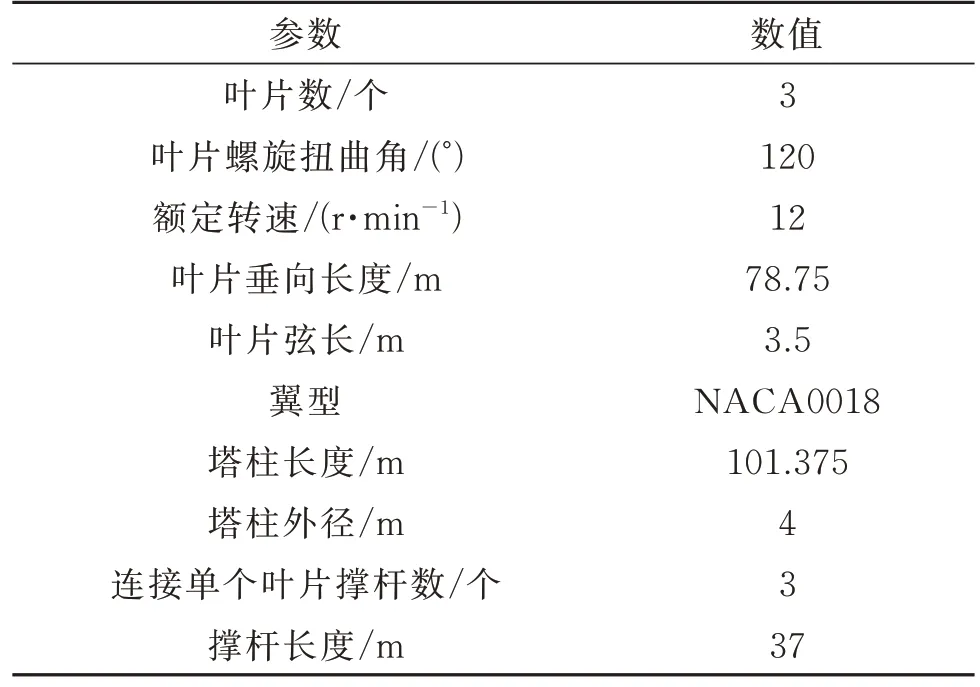
表1 螺旋型风机参数Tab.1 Parameters of the helical type wind turbine
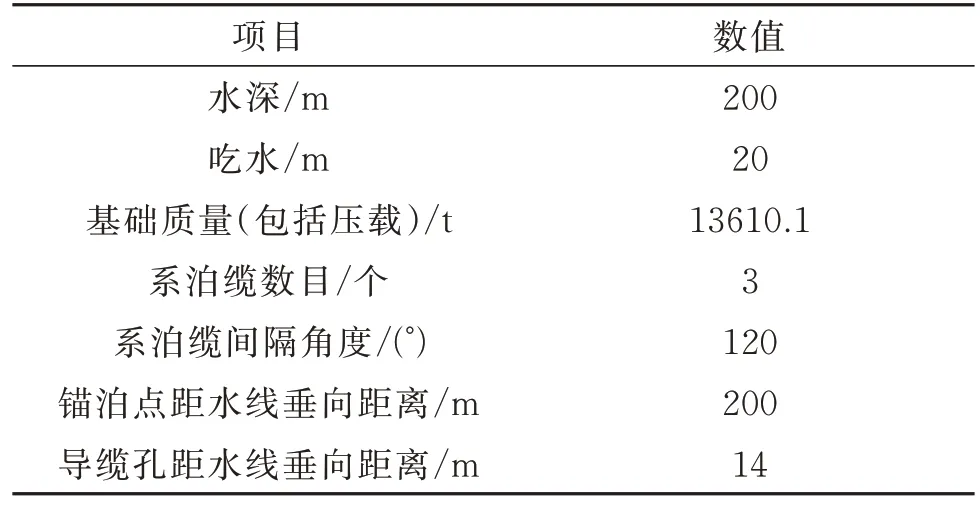
表2 浮式基础及系泊系统参数Tab.2 Parameters of the floating foundation and mooring system

图1 浮式螺旋型垂直轴风机示意图Fig.1 Schematic diagram of the helical type floating vertical axis wind turbine
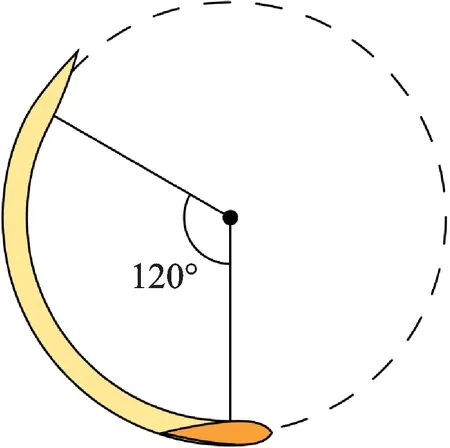
图2 120°螺旋扭曲角情况下风机叶片俯视图Fig.2 Top view of the blade with 120° helical twist angle
2 浮式风机建模方法
2.1 坐标系统
为了描述风机结构的动力响应,建立一系列坐标系如图1 所示,包括惯性坐标系,浮式基础浮动坐标系,塔柱浮动坐标系,以及叶片浮动坐标系。坐标系统的坐标轴分别用Xi,Yi,Zi(i=0,1,2,3)描述。惯性坐标系的X0轴与风浪同向,Z0轴方向垂直向上;浮式基础浮动坐标系用于描述基础的六自由度运动,其原点位于浮式基础的重心处,X1轴沿着基础运动纵荡方向,Z1轴沿着基础运动垂荡方向;塔柱浮动坐标系用于描述塔柱的变形,其原点位于塔柱根部,X2轴与浮式基础浮动坐标系的X1轴平行,Z2轴沿着塔柱高度方向;叶片浮动坐标系用于描述叶片的变形,其原点位于叶片底部,X3轴垂直于撑杆方向,Z3轴沿着叶片高度方向垂直向上。坐标系间通过卡尔丹角进行相互转换。通过浮动坐标系的定义,可以实现塔柱和叶片的大范围运动和自身变形的耦合。
2.2 柔性塔柱与叶片建模方法
浮式螺旋型风机在运行过程中,由于浮式基础运动、风轮转动等因素的影响,塔柱和叶片在自身产生变形的同时会发生大范围运动。下文以叶片为例说明柔性体建模方法。
将螺旋叶片处理为可大范围运动且考虑扭转变形的曲梁模型,如图3 所示。基于有限元方法,将弯曲叶片离散为若干直梁单元。每个叶片单元节点考虑六自由度变形,包括沿横向(x,y向)的弯曲变形和弯曲角度,沿轴向(z向)的拉伸变形,以及绕轴向的扭转角度。图3 中为惯性 坐标系,为叶片 浮动坐标系,叶片变形前任一点P0变形后表示为P。则P点相对于惯性坐标系原点O0的矢径r可以表示为:
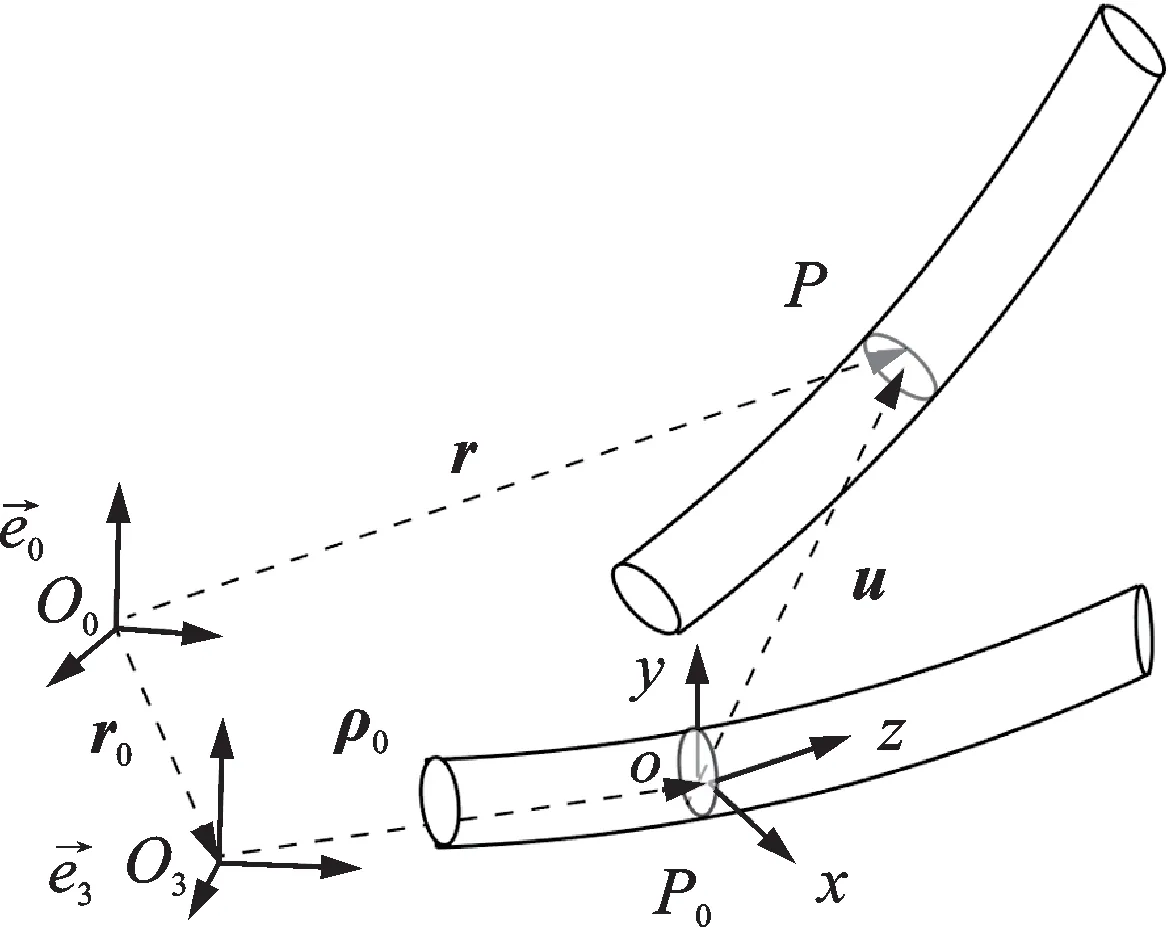
图3 大范围运动的柔性曲梁模型Fig.3 Flexible curve beam model with large overall motion
式中r0为叶片浮动坐标系相对惯性坐标系的矢径,ρ0为P0点相对 于的矢径,u为P0点的变 形位移。
为了描述变形位移u,将叶片划分为若干直梁单元,并在每个单元上建立单元坐标系。基于连续介质力学,u可以表示为:
式中Ni(i=1,2,3)表示单元形函数,耦合项H可由Ni表示[11],p为基于叶片浮动坐标系的变形位移列阵。
得到变形位移u之后代入到式(1)中可以描述矢径r,由此建立叶片大范围运动与自身变形的耦合关系。之后基于若丹速度变分原理可以建立叶片柔性体动力学方程:
式中 δWb为广义外力虚功率,δTb和δPb分别为惯性力虚功率以及弹性力虚功率。
塔柱的建模方法与叶片类似,区别在于建模过程中需要将梁模型的弯曲角度设置为0°。
2.3 松耦合建模方法
本文采用松耦合方法建立浮式风机系统数值计算模型,基本的建模思路如图4 所示。
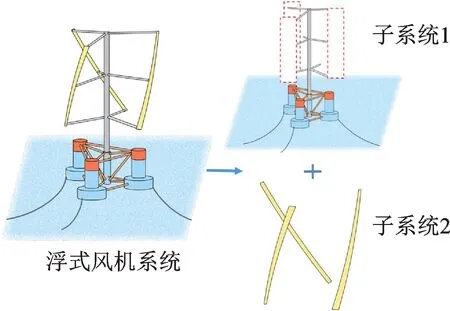
图4 松耦合建模方法示意图Fig.4 Schematic diagram of the slack coupled modeling method
首先,将整个风机系统分为两个子系统,子系统1 中包含风机的所有结构,其中将浮式基础处理为刚体,考虑纵荡、横荡、垂荡、橫摇、纵摇以及艏摇六自由度运动;将柔性塔柱处理成弹性体,将叶片处理为等效质量点,考虑其质量及转动惯量。此后基于若丹速度变分原理建立子系统1 的动力学方程。考虑约束条件后,最终得到的拉格朗日方程如下式所示:
式中M为质量矩阵;Q为广义外力矩阵;Φq,λ和γ分别为约束方程的雅克比矩阵、拉格朗日乘子和加速度约束方程右项。q为子系统1 全体自由度广义坐标,包括浮式基础运动、塔柱变形以及叶片质量点的运动。
子系统2 中包括柔性叶片。将子系统1 计算得到的叶片质量点运动代入到子系统2 中,基于若丹速度变分原理可以计算得到叶片弹性变形;可以由式(3)计算得到叶片弹性变形。
2.4 环境载荷计算
浮式风机处于复杂的海洋环境中,本文考虑的海上浮式风机外载荷包括风轮气动载荷、塔柱风压载荷、波浪载荷以及系泊载荷。风轮气动载荷采用双制动盘多流管理论进行模拟[12];塔柱风压载荷运用经验公式进行计算[13];采用悬链线理论[14]建立系泊系统模型,可以得到系泊恢复力;对于波浪载荷,采用SESAM/Wadam 模块进行水动力参数的计算,包括波浪力传递函数、附连水质量、静水恢复刚度和势流阻尼,之后将水动力参数导入到数值程序中计算得到波浪载荷。
2.5 数值程序计算流程
基于上述风机系统建模方法及环境载荷计算方法,编制浮式螺旋型垂直轴风机动力响应计算程序。计算流程如图5 所示。

图5 数值计算程序流程图Fig.5 Procedure of the numerical calculation
如图5 所示,在每一时间步中,首先计算风机外载荷,包括水动力载荷、系泊载荷以及气动载荷等。之后将这些外载荷导入到子系统1 中作为式(4)中的广义外力项,其中波浪载荷以及系泊载荷施加到浮式基础上,风压载荷以均布力的形式施加到塔柱上,气动载荷作用于风轮盘面。可以计算得到该时刻叶片大范围运动、塔柱变形以及浮式基础运动。此后,将浮式基础运动重新导入到外载荷计算模块中,可以得到下一时间步的风机系统外载荷,由此实现外载荷与结构动力响应的耦合。此外,同时将叶片的大范围运动以及气动载荷导入到子系统2 中,气动载荷作为式(3)中的广义外力虚功率项,数值求解可以得到叶片弹性变形。
2.6 数值程序验证
目前浮式垂直轴风机商用计算软件较少,已发表的大型浮式螺旋型风机的动力响应计算结果几乎没有。Liu 等[15]开发了浮式垂直轴风机单刚体计算程序,并采用模型试验方法对计算结果进行了验证。因此,选用上述刚体程序与本文提出的松耦合计算程序进行对比,验证螺旋型风机浮式基础运动计算结果的准确性。
选取定常风与规则波作用下的额定工况,风速为15 m/s,波高和周期分别为3.62 m 和10.29 s,分别用两种程序计算得到螺旋型风机浮式基础运动,结果如图6 所示。两种程序得到的运动时程曲线吻合较好,说明本文的松耦合计算程序可以准确计算螺旋型风机浮式基础的运动。

图6 浮式基础运动对比Fig.6 Comparison of the motions of floating foundation
为了验证叶片建模的正确性,在有限元软件ANSYS 中建立相同参数的叶片模型,通过模态计算得到直叶片和120°螺旋叶片的固有频率,并与本文的数值程序计算得到的结果进行对比,如表3所示。

表3 叶片固有频率对比(单位:rad·s-1)Tab.3 Comparison of the natural frequencies of blades(Unit:rad·s-1)
表3 中所示为直叶片和120°螺旋叶片前三阶固有频率的对比结果。120°螺旋叶片的数值程序的一阶和二阶固有频率与ANSYS 相比结果差异较为明显,这可能是因为数值程序使用了欧拉-伯努利梁模型,相比于ANSYS 建模中使用的铁木辛柯梁模型,不能有效考虑剪切变形的影响。但整体而言,数值程序和ANSYS 计算结果差异较小,说明本文建立的模型可以较为准确地模拟风机叶片的动力响应特性。
3 计算结果分析
本节计算风浪联合作用下浮式螺旋型风机的动力响应,并与直叶片风机进行对比,主要研究螺旋扭曲角对气动转矩、浮式基础运动以及叶片变形产生的影响。首先根据网格收敛性分析,将塔柱划分为6 个单元,单根叶片划分为12 个单元。之后定义计算工况,本研究选择风机运行额定工况,选取同向的随机波与湍流风。其中随机波选用Jonswap 谱进行模拟,湍流风选用Kaimal 风谱进行模拟。计算工况的相关参数如表4 所示。

表4 额定工况参数Tab.4 Parameters of the rated cases
3.1 气动转矩
计算风机动力响应后,将气动转矩的时域结果进行统计,得到平均值与标准差的对比结果,如表5所示。在额定工况下,相比于直叶片,螺旋扭曲角为120°的风轮气动转矩的平均值不发生变化,但标准差明显减小。因此可以得到初步结论:对于直叶片浮式垂直轴风机来说,设计合适的叶片螺旋扭曲变异可以显著减小转矩波动,这有助于减小风机功率输出的不稳定性并减轻叶片在风机运行过程中的疲劳。

表5 气动转矩统计结果(单位:N·m)Tab.5 Statistical results of aerodynamic torque(Unit:N·m)
为了进一步分析影响气动转矩的因素,对气动转矩时域曲线进行傅里叶变换得到幅值谱。图7 所示为气动转矩的幅值谱对比。对于直叶片情况,气动转矩频率成分较为复杂,主要包括湍流风频率,3P 和6P 频率。1P 频率代表着风轮旋转频率,在风机运行过程中,三根叶片旋转会产生3P 频率。此外,可以看到湍流风在低频范围内对气动转矩产生了较大的影响。
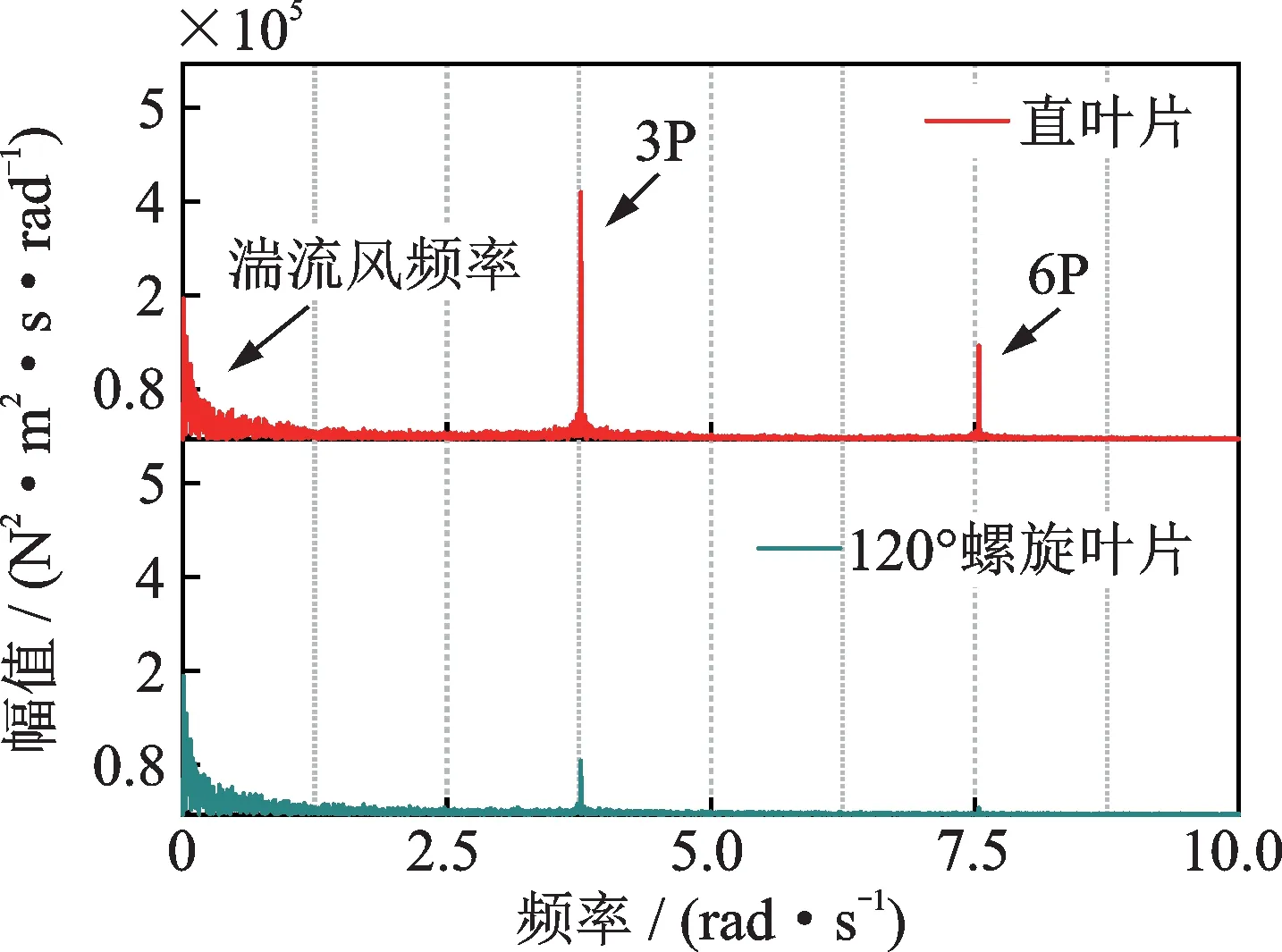
图7 气动转矩幅值谱Fig.7 Amplitude spectra of aerodynamic torque
相比于直叶片情况,120°螺旋型风机的转矩波动显著减小,表现出和统计结果相同的规律。其中主要的频率成分包括湍流风频率以及3P 频率。相比于直叶片情况,湍流风频率的幅值基本没有变化,而3P 频率成分的幅值明显降低。
3.2 浮式基础运动
本节研究浮式垂直轴风机叶片螺旋扭曲设计对浮式基础运动的影响,分析基础运动与气动载荷之间的关系。由于风浪沿着基础纵荡方向(见图1),因此给出浮式基础的纵荡、垂荡以及纵摇三个主要方向的运动统计结果,如表6 所示。

表6 浮式基础运动统计结果Tab.6 Statistical results of motions of floating foundation
在直叶片风机和120°螺旋型风机两种情况下,基础运动的平均值和标准差都相差不大,这表明螺旋扭曲变异设计对基础运动的影响很小。这是因为波浪载荷主要影响基础运动的幅值而气动载荷主要影响基础运动的平衡位置[16]。两种情况下环境载荷的设置相同,因此波浪载荷与湍流风载荷对基础运动的影响没有差别。螺旋扭曲角的设计主要影响气动转矩的波动,而对气动转矩的平衡位置几乎没有影响(见表5)。气动力的波动相比于波浪载荷来说非常小,所以对基础运动的影响也很小。因此,可以说明叶片螺旋扭曲变异设计对基础运动几乎没有影响。
图8 为浮式基础运动幅值谱的对比。直叶片风机和120°螺旋型风机两种情况的频率成分相同,主要包括波浪频率成分以及低频的湍流风频率成分。湍流风对纵荡运动产生了较大影响,这可能是由于在低频范围内,湍流风激发了纵荡方向的固有频率。湍流风对纵摇运动影响较小,而在垂荡方向几乎没有影响。此外,值得注意的是由于垂荡和纵摇的固有频率与波浪频率较为接近,因此在这两个方向上,波浪频率激发了它们的固有频率,在实际工程中需要对这一现象加以考虑。
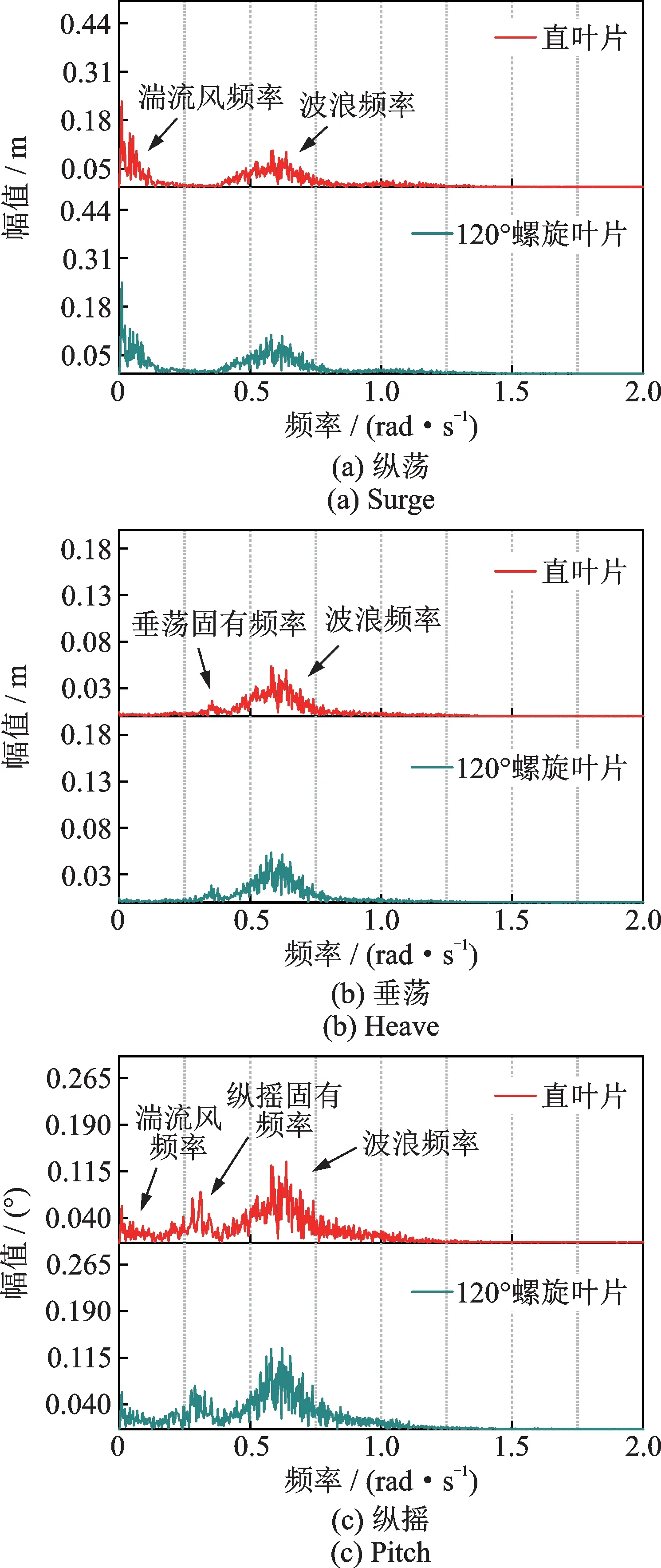
图8 浮式基础运动幅值谱Fig.8 Amplitude spectra of motions of floating foundation
3.3 塔柱变形
作为连接浮式基础与叶片的中间结构,塔柱的动力响应对于风机运行安全十分重要。本节选取塔柱顶端节点为研究对象,比较直叶片风机和120°螺旋型风机两种情况下塔顶X2向和Y2向的变形,统计结果如表7 所示。
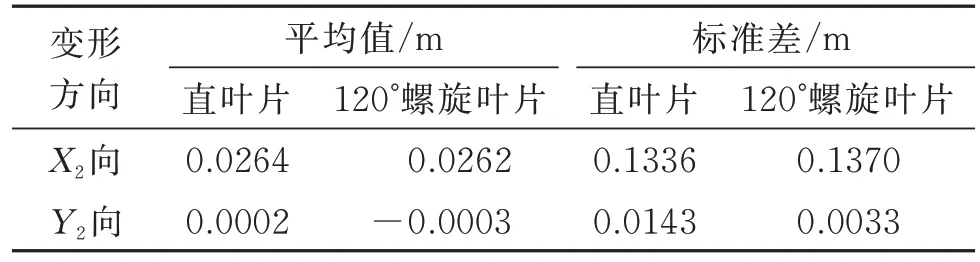
表7 塔顶变形统计结果Tab.7 Statistical results of tower top deformation
整体来看,在风浪载荷作用下,塔柱X2向变形远大于Y2向。对于X2向,两种风机塔顶变形的平均值与标准差几乎相等。而对于Y2向,120°螺旋型风机的塔顶变形远小于直叶片风机,这有利于降低塔柱在风机运行过程中产生的结构疲劳。
进一步对比分析塔顶变形的影响因素,对两个方向的塔顶变形时程曲线进行傅里叶变换,得到幅值谱如图9 所示。
如图9 所示,塔顶X2向变形频率成分比较复杂,主要包括波浪频率,3P 频率和塔柱固有频率成分,其中塔柱固有频率可能由湍流风作用而激发。塔顶Y2向变形主要为风轮3P 频率,此外,也出现了较小的塔柱固有频率成分。总体来看,因为120°螺旋叶片设计可以减小气动转矩的3P 频率,因此塔柱变形的3P 频率成分相应减小。而直叶片风机塔柱Y2向变形主要受到3P 频率的影响,因此在叶片螺旋扭曲变异设计后,Y2向变形大幅降低。
3.4 叶片变形
叶片单元节点的变形可以分解为沿着Z3轴的垂向变形与在X3-Y3平面内的横向变形。如2.1 节所述,叶片浮动坐标系的Z3轴沿着叶片高度方向垂直向上,由于叶片细长的结构,其节点的垂向变形相比于横向变形来说很小,因此本文对叶片单元节点的横向变形进行研究。图10 以叶片中间点为例说明螺旋叶片变形分解方向。因为本文研究的叶片螺旋扭曲角为120°,所以叶片中间点对应的螺旋扭曲角为60°。叶片节点横向变形可以分解为法向变形和切向变形,其中法向变形垂直于叶片翼型方向,切向变形沿着叶片翼型方向。
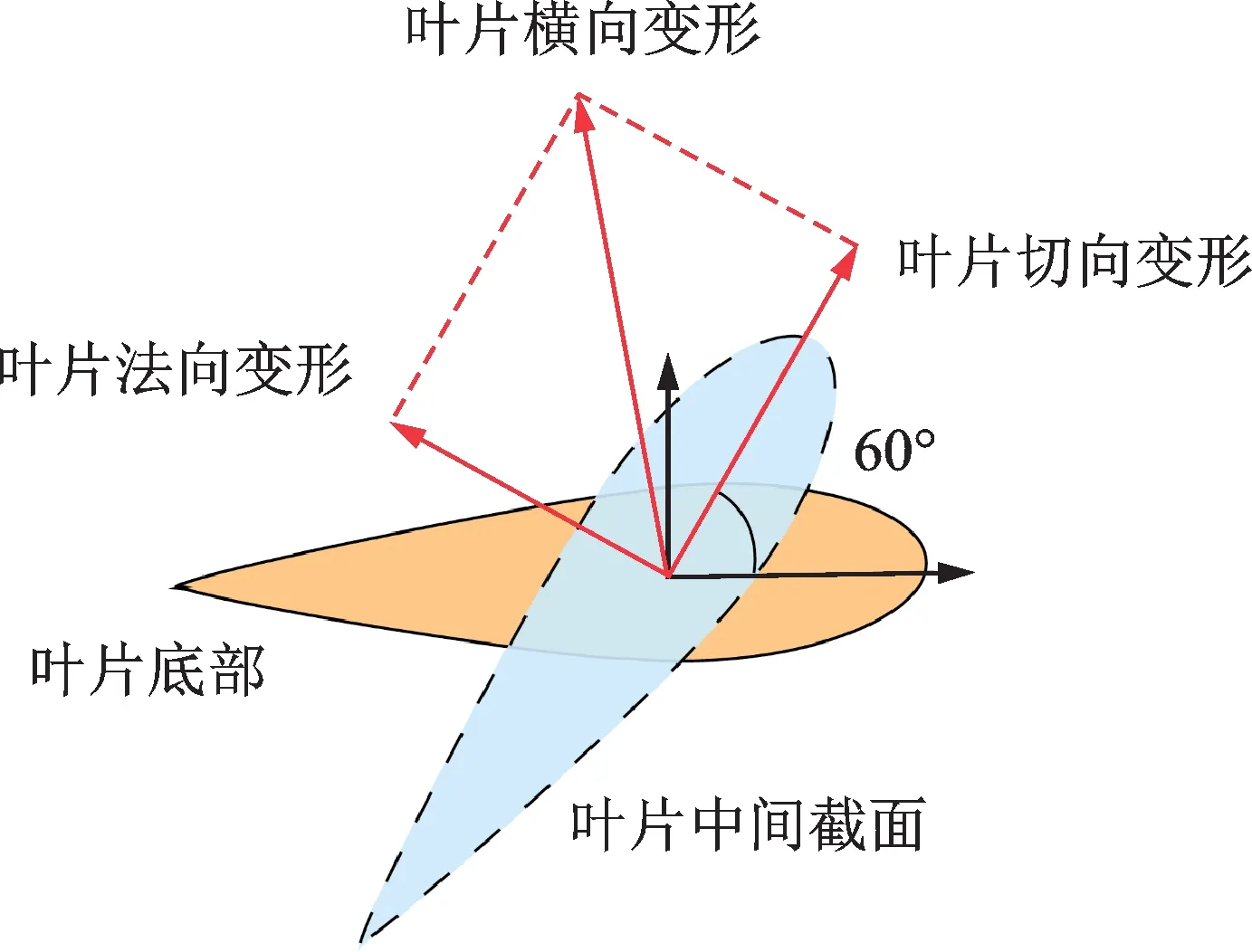
图10 叶片中间节点变形分解Fig.10 Resolution of deformation on middle node of the blade
如前所述,单根叶片划分为了12 个单元,因此共有11 个中间节点。取叶片第9 节点为例研究螺旋型风机叶片的动力响应特性,计算得到的切向及法向节点变形统计结果如表8 所示。

表8 叶片第9 节点变形统计结果Tab.8 Statistical results of blade deformation on node 9
对于直叶片风机,叶片法向变形远大于切向变形。这是因为沿着整根叶片,法向变形垂直于叶片翼型方向(见图10),法向刚度相对于切向刚度来说很小,在外载荷作用下,叶片变形主要表现为法向变形。相比于直叶片,120°螺旋叶片的法向变形波动显著减小,变形平衡位置也降低到0 附近。而切向变形有所增大。整体来看,在风浪联合作用下,120°螺旋叶片变形远小于直叶片,这说明浮式垂直轴风机螺旋变异设计可以减小风机运行过程中叶片的变形。这有助于提高叶片可靠性,增加风机使用寿命。
为了进一步研究叶片动力特性,对叶片变形时程曲线进行傅里叶变换,得到叶片第9 节点法向变形与切向变形幅值谱,如图11 所示。
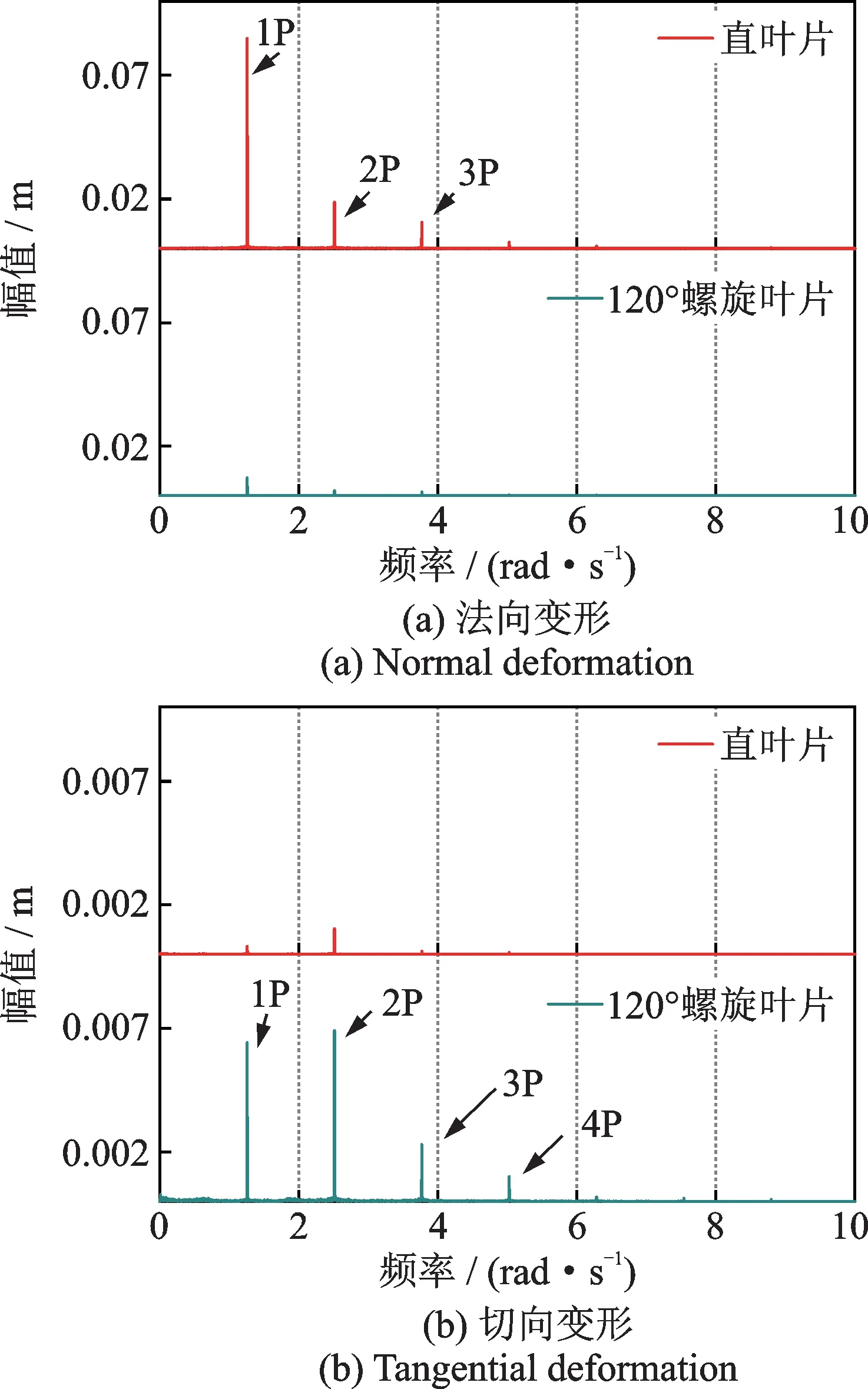
图11 叶片第9 节点法向变形与切向变形幅值谱Fig.11 Amplitude spectra of normal deformation and tangential deformation on node 9 of the blade
如图11 所示,叶片第9 节点切向变形与法向变形幅值谱表现出与叶片统计结果相同的规律。叶片法向变形主要包括1P,2P,3P 频率成分,其中1P 为主要频率成分。相对于直叶片风机,120°螺旋叶片的法向变形减小。叶片切向变形主要包括1P~4P频率成分,相对于直叶片风机,120°螺旋叶片的切向变形相对增大。在浮式螺旋型风机设计制造过程中,为避免结构共振,需要对叶片进行合理设计,使得叶片自身固有频率远离1P 频率及其倍频。
4 结论
本文基于一种松耦合方法建立三叶片5 MW 浮式螺旋型垂直轴风机计算模型。编写数值求解程序,计算风浪联合作用下的风机动力响应,并与直叶片风机进行了对比。主要结论如下:
(1)相较于直叶片风机,合理的螺旋扭曲变异设计可以显著减小气动转矩的波动,气动转矩频率成分较为复杂,主要包括湍流风频率以及3P 频率。其中,湍流风在低频范围内对气动转矩产生了较大的影响。因此,对于浮式螺旋型风机来说,如果想进一步减小气动转矩波动,提高功率输出稳定性,可以对控制系统进行设计优化,从而减小湍流风对气动转矩的影响。
(2)叶片螺旋扭曲变异设计对基础运动影响很小。在直叶片风机和螺旋型风机两种情况下,基础运动几乎不发生变化。基础运动主要包括波浪频率成分以及低频的湍流风频率成分。此外,由于垂荡和纵摇的固有频率与波浪频率较为接近,因此在这两个方向上,波浪频率激发了它们的固有频率,在实际工程中需要对这一现象加以考虑。
(3)对于螺旋型风机来说,其塔顶X2向变形与直叶片风机大体相等,而塔顶Y2向变形远小于直叶片风机,这有利于降低塔柱在风机运行过程中产生的结构疲劳。直叶片风机塔顶X2向变形频率成分主要包括波浪频率、3P 频率和塔柱固有频率成分,塔顶Y2向变形主要为风轮3P 频率。螺旋型叶片设计可以显著减小塔柱变形的3P 频率成分。此外,湍流风可能会激发塔柱的固有频率,在对风机塔柱进行设计时,需要注意这一现象。
(4)螺旋型风机叶片振动明显小于直叶片风机,浮式垂直轴风机螺旋变异设计可以减小风机运行过程中叶片的变形。这在一定程度上有助于提高叶片的可靠性,增加叶片的疲劳寿命。对于直叶片风机,叶片法向变形远大于切向变形。对于120°螺旋型风机,叶片的法向变形波动显著减小,而切向变形有所增大。螺旋叶片变形频率成分主要包括1P 频率成分及其倍频。在浮式螺旋型风机叶片设计过程中,需要使叶片自身固有频率远离上述频率,以避免结构共振。
