遗忘因子递推最小二乘法辨识锂离子电池参数
2024-01-10曹以龙杜君莉史书怀
赵 转,曹以龙,杜君莉,史书怀*
(1. 郑州电力高等专科学校电力工程学院,河南 郑州 450000; 2. 上海电力大学电子与信息工程学院,上海 200438; 3. 国网河南省电力公司电力科学研究院,河南 郑州 450000)
在锂离子电池的测试和实际使用中,需要对荷电状态(SOC)进行准确估计[1]。 锂离子电池的等效电路模型是大多数SOC 估计算法的重要基础,如扩展卡尔曼滤波、自适应扩展卡尔曼滤波等。
目前,电池等效电路模型主要包括内阻(Rint)模型[2]、新一代汽车合作伙伴计划(PNGV)模型[3]、Thevenin 模型[4]和n阶RC 等效电路模型[5]。 Rint 模型是由直流电源和内阻组成的内阻模型,结构简单、不考虑电池的内部状态,属于一种理想的模型,一般只用于简单的电路仿真。 考虑电容特性的PNGV 模型可准确反映放电过程,但对充电过程的反映不佳。n阶RC 电路等效模型能反映电池内部参数与动态参数之间的关系,但模型的复杂度随着阶数的增加而增加,不利于实时在线计算。 等效电路模型通常选择二阶RC 模型,不仅精度和动态仿真特性良好,而且复杂度较低。
锂离子电池内部有复杂的化学反应和物理结构,实际使用时,内部状态会受到环境温度、操作条件和电池老化程度等因素的影响[6]。 一些参数在电池等效模型中会随着工作条件的变化而变化,因此,实时且准确地辨识电池等效参数模型中的参数很有必要。 递推最小二乘(RLS)法[7]是常用的系统参数在线辨识方法,具有简单稳定的特点,但随着递推过程中数据的增加,新数据的生成会受到旧数据的影响,导致较大的误差。 为此,本文作者提出遗忘因子递推最小二乘(FFRLS)法,RLS 中引入遗忘因子,来调整新旧数据的比例,使算法能更快地收敛到实际值。 建立二阶RC 等效电路模型,应用FFRLS 在线辨识等效电路模型参数,通过动态应力测试实验验证FFRLS 算法的实时性和准确性。
1 锂离子电池建模
1.1 等效电路模型
锂离子电池的二阶RC 等效电路模型如图1 所示。
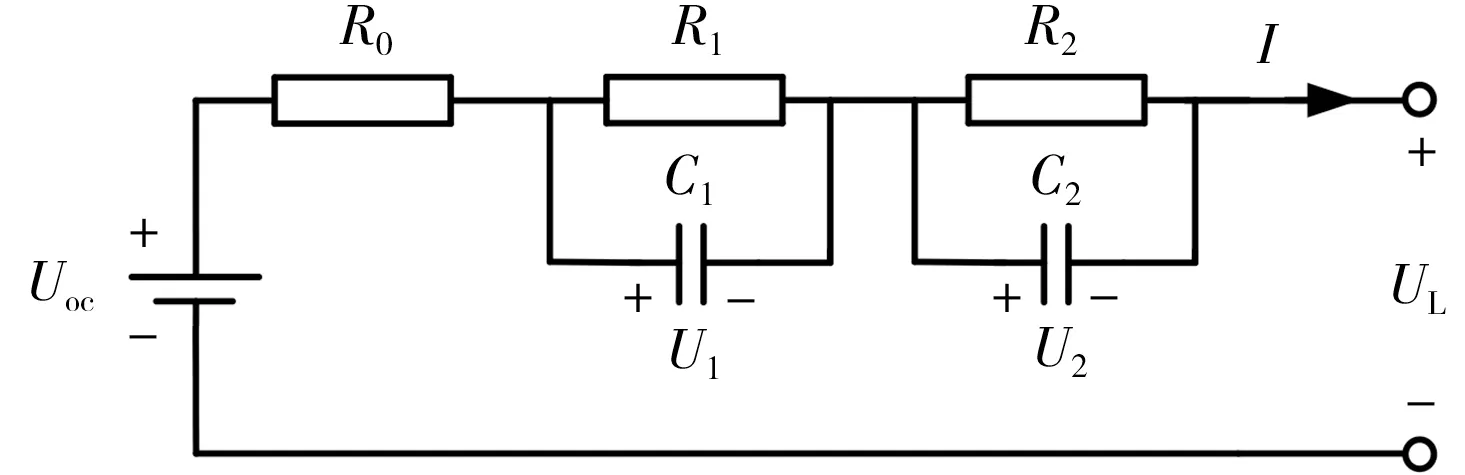
图1 二阶RC 等效电路模型Fig.1 Second-order RC equivalent circuit model
该模型由理想电压源Uoc、欧姆电阻R0和两个RC 并联电路组成。Uoc表示电池的开路电压;R0为电池内阻;R1和C1为电池电化学极化内阻和电容;R2和C2为浓度极化效应内阻和电容;UL为电池端电压;I为输入电流。
1.2 等效电路状态方程
根据图1 以及电路原理,该模型时域下的电气特性方程见式(1)。
式(1)中:Uoc(SOC(t))表示开路电压Uoc是SOC 的函数;t为时间。
式(1)写成频域下表达式,即式(2)。
式(2)中:E(s)表示端电压与开路电压的差值;s为复频域下的变量。
将式(2)写成传函形式,如式(3)所示。
式(3)可整理为式(4)。
双线性变换公式见式(5)。
式(5)中:T为采样时间;z表示离散域。
令τ1=R1C1、τ2=R2C2,将式(5)代入式(4)中,得到式(6)。
式(6)中:k为变量;k1~k5为系数,如式(7)所示。
定义参数a、b、c、d、e,如式(8)所示。
将式(8)代入式(7)中,简化为式(9)。
电池内阻和电容参数整理为式(10)。
2 电池参数辨识方法
2.1 递推最小二乘(RLS)法
RLS 法是常用的系统参数辨识方法,以离散函数的平方准则为理论基础,获取辨识的参数。 基本原理见式(11)。
式(11)中:φ(t)为观测数据矩阵;θ为参数矩阵。
RLS 算法的参数辨识如式(13)所示。
式(14)中:P(k)为协方差矩阵;K(k)为增益矩阵;e(k)为误差;y为输出变量;I为单位矩阵。
2.2 遗忘因子递推最小二乘(FFRLS)法
FFRLS 算法是在RLS 算法的基础上,在观测数据矩阵和系统输出向量中加入遗忘因子λ作为系数,如式(14)所示。当每个观测值获得新数据时,通过指数加权调整新旧数据的比例,然后进行加权平均,修正最终获得的识别参数。 因此,当输入变量发生变化时,随着系统观测数据的增加,FFRLS算法能够更快速响应并获得较好的辨识参数。
当λ=1 时,FFRLS 算法退化为RLS 算法,由于λ是常数,当在线辨识参数误差很小时,引入λ反而会增大在线辨识参数误差。 当在线辨识参数误差很大时,则可以通过优化λ来加快在线辨识的收敛速度,从而减小误差。 选择合适的λ,不仅可以提高收敛速度,还可以减小误差。
3 实验验证和分析
实验用电池测试设备为BTS-60V100A 测试系统(深圳产)。 该设备可设定电压电流的大小,以满足不同充放电工况,为验证实验提供相关数据。 以IFP36130155-36Ah 型磷酸铁锂锂离子电池(山东产)为研究对象,参数见表1。
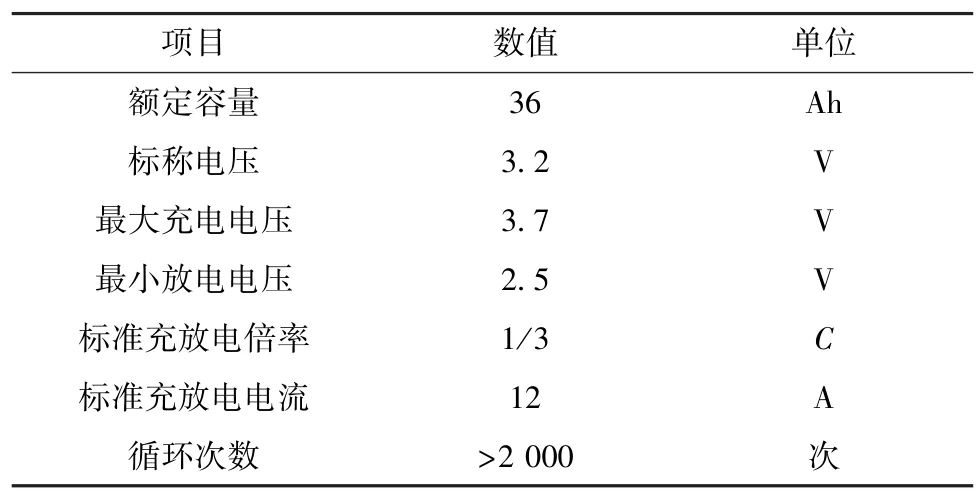
表1 磷酸铁锂锂离子电池参数Table 1 Parameters of lithium iron phosphate Li-ion battery
3.1 开路电压(OCV)-SOC 曲线
OCV-SOC 曲线是锂离子电池建模过程中的一个重要组成部分。 由于存在极化和迟滞效应,仅在电池充分静置条件下,OCV 才与端电压近似相等,因此OCV 为静态参数。
根据间歇恒流充电和放电实验数据,提取每次静置结束时刻的SOC(SOC)和对应的OCV,对充放电OCV 平均值进行拟合,得到OCV-SOC 拟合结果,如式(15)所示。
为了减小迟滞特性产生的误差,对充放电实验中OCV平均值进行8 次多项式拟合,拟合曲线如图2 所示。

图2 OCV-SOC 拟合曲线Fig.2 Fitting curves of open circuit voltage (OCV)-state of charge(SOC)
3.2 动态工况测试
动态工况实验(DST)可模拟电池在实际道路工况下的随机充放电工况,该工况是以美国联邦城市道路工况为基础简化而来的。 实验以SOC=100%为开始,在一个周期内,以不同电流(-12 A、-9 A、0 A、9 A、12 A 和18 A 等)对电池进行充放电,循环若干个周期,以SOC=0 为结束,模拟电池电量被耗尽的整个周期。 电压电流的曲线如图3 所示,其中,电流大于0,定义为电池放电,电流小于0,定义为给电池充电。
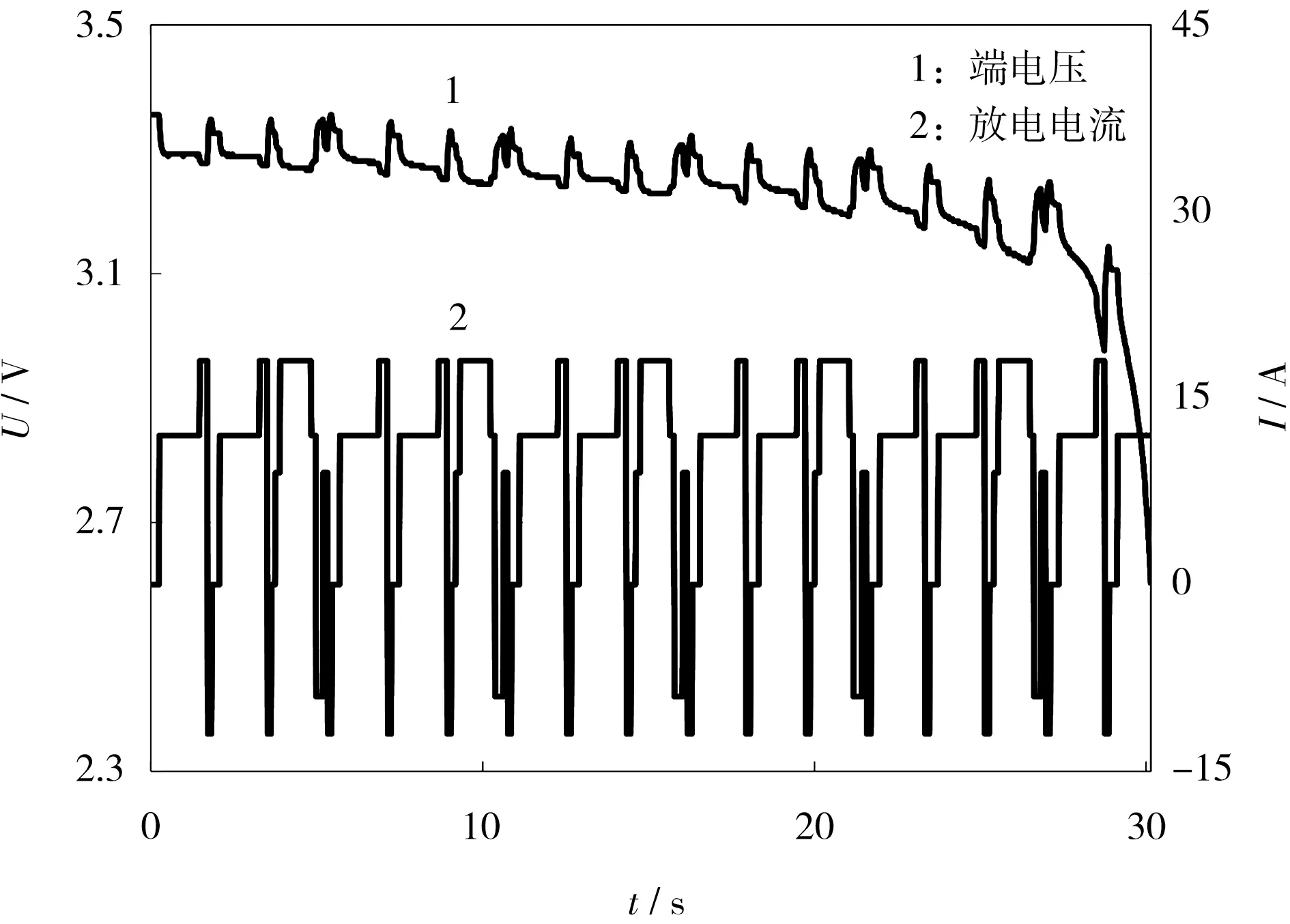
图3 DST 实验时的输入电流与端电压测量曲线Fig.3 Measurement curves of input current and terminal voltage under dynamic stress test (DST) experiment
从图3 可知,大约存在6 个周期可放空电量。
3.3 电池参数辨识结果
为了验证所提参数辨识方法的有效性,首先在离线状态下对电池参数结果进行辨识,以此为基准,与在线辨识方法进行比较,检验在线辨识方法的准确性。 离线参数辨识的结果如图4 所示。 所采用的离线辨识方法为传统的电路微分求解方法,通过分段拟合的形式获得不同SOC 值对应的电池参数。

图4 离线参数辨识结果 Fig.4 Offline parameter identification results
从图4 可知,电池内阻R0的值约为1 mΩ,电化学极化电阻R1和电容C1的值分别约为3 mΩ 和1 000 F,浓差极化电阻R2和电容C2的值分别约为2 mΩ 和50 000 F。 离线辨识的参数结果为在线实时辨识方法提供了比较基准。
RLS 算法和FFRLS 算法在DST 条件下识别的参数曲线分别见图5 和图6。

图5 RLS 算法辨识结果 Fig.5 Identification results of recursive least square (RLS) algorithm
图5 和图6 的结果均在离线参数值附近波动,体现了在线参数辨识算法的准确性。 对比图5 和图6 可知,RLS 算法识别的参数相对稳定,但对动态参数变化的识别能力不足。而FFRLS 算法识别的参数具有明显的波动性,更准确地反映了动态工况下电流切换时电池内部发生复杂变化的特性。
为了更好地研究FFRLS 算法特性以及λ对端电压均方根误差的影响,λ取0.80~1.00,精度为0.02,记录各个λ对应的端电压均方根误差,确定最优的λ取值范围。 当λ=1.00 时,FFRLS 算法等效为RLS 算法。 不同λ下的端电压均方根误差见表2。

表2 不同λ 下的端电压均方根误差Table 2 Root mean square error of terminal voltage with different forgetting factors(λ)
从表2 可知,与RLS 算法相比,采用FFRLS 算法的端电压均方根误差较小。 随着λ的加入,当λ从1.00 逐渐减小时,端电压均方根误差也随之减小,直至λ=0.84 时,端电压均方根误差反而增大,表明λ在一定区间范围内具有正向优势,符合理论说法,λ的值不能过大或过小。 根据表2 的数值可知,当λ=0.86~0.94 时,电池模型精度达到最佳范围。
4 结论
本文作者分析了锂离子电池的二阶RC 等效电路模型,研究了基于RLS 算法和FFRLS 算法的等效电路模型参数在线识别算法。 通过DST 实验验证了充放电情况下等效电路模型参数识别的正确性,并对不同λ下模型参数得到的预测端电压与实际端电压进行了比较,选择合适的λ。 实验结果表明,与RLS 算法相比,FFRLS 算法具有更精确的参数识别能力。 此外,通过对比不同λ下的端电压均方根误差可知,λ=0.86~0.94 为最佳范围。
