地铁列车荷载下类矩形隧道结构动力响应分析

杜明芳，杨晓晨，王 倩，张 鹏

（河南工业大学土木工程学院，河南 郑州 450001）

近年来，随着地铁等地下工程的不断发展，地下结构类型不断增多。类矩形隧道作为单洞双线隧道的一种结构类型，相较于传统单洞双线隧道，具有结构断面尺寸小、能够充分利用地下空间资源等优点，可以最大程度地降低对周边环境的影响［1］。因此，准确评估类矩形隧道在地铁行车荷载作用下的稳定性尤为重要。

在隧道结构动力响应的相关研究中，许多学者利用试验及数值模拟等手段，取得了一系列有重要意义的成果。王国才等［2］使用数值模拟的方法分析不同时速下隧道结构和周围土体的动力响应，得到了地铁列车荷载下隧道结构和软土的动力响应和沉降特性；周捡平等［3］通过试验与模拟对比分析的方法研究地铁列车荷载作用下软土地基的动力响应和累计塑性变形；刘志强等［4］通过试验和数值模拟的方法进行对比，研究地铁列车循环荷载作用下隧道下卧土层中加速度峰值和沉降变形等的变化规律；王涛等［5］基于南京地铁2号线沉降监测数据，采用2.5维数值模拟与分层总和法，探究了粉细砂地层在地铁行车荷载作用下的动力响应与变形规律；胡豹等［6］采用有限元模型分析的方法，研究了单洞双线隧道在地铁列车交会情况下的动力响应规律；张啟乐等［7］以宁波地铁3号线类矩形隧道为背景，分别对类矩形盾构隧道与圆形盾构隧道等两种隧道模型进行模态分析和振动特性对比，研究二者振动特性的不同。现阶段对于隧道结构动力响应问题的研究大多基于常见单洞隧道结构或者大断面单洞双线隧道结构，对于类矩形隧道结构的研究较少。

本文以郑州地铁隧道为背景，建立地铁车辆－隧道－土体相互作用的三维有限元模型，分析类矩形隧道在地铁列车荷载作用下的动力响应。

1 工程概况

郑州市地铁8号线起于西部新城荥阳组团的荥华路站，止于东部新城中牟组团的中牟北站。线路全长51.482 km，均为地下线，设车站29座，其中换乘站11座。郑州东站前后段（畅和街站—郑州东站—圃田西站区间）共有两段类矩形盾构段，如图1所示。本文以畅和街站至郑州东站类矩形盾构段为研究对象。此段工程地形较为平坦，地面高程约84.97～89.45 m，地貌单元属黄河冲洪积平原。隧道中心埋深约为22.5 m，类矩形盾构段长度为83 m，类矩形隧道管片尺寸为11.5 m×6.937 m，衬砌为450 mm厚的C50混凝土，中间有350 mm厚后浇中隔墙（见图2）。

图2 类矩形隧道断面示意图（单位：mm）

2 三维模型建立

2.1 参数选取

场地勘察报告显示，地下61 m深度范围内的土层主要由粉质黏土、粉土与粉细砂构成。土体各层物理力学参数与结构计算参数见表1。

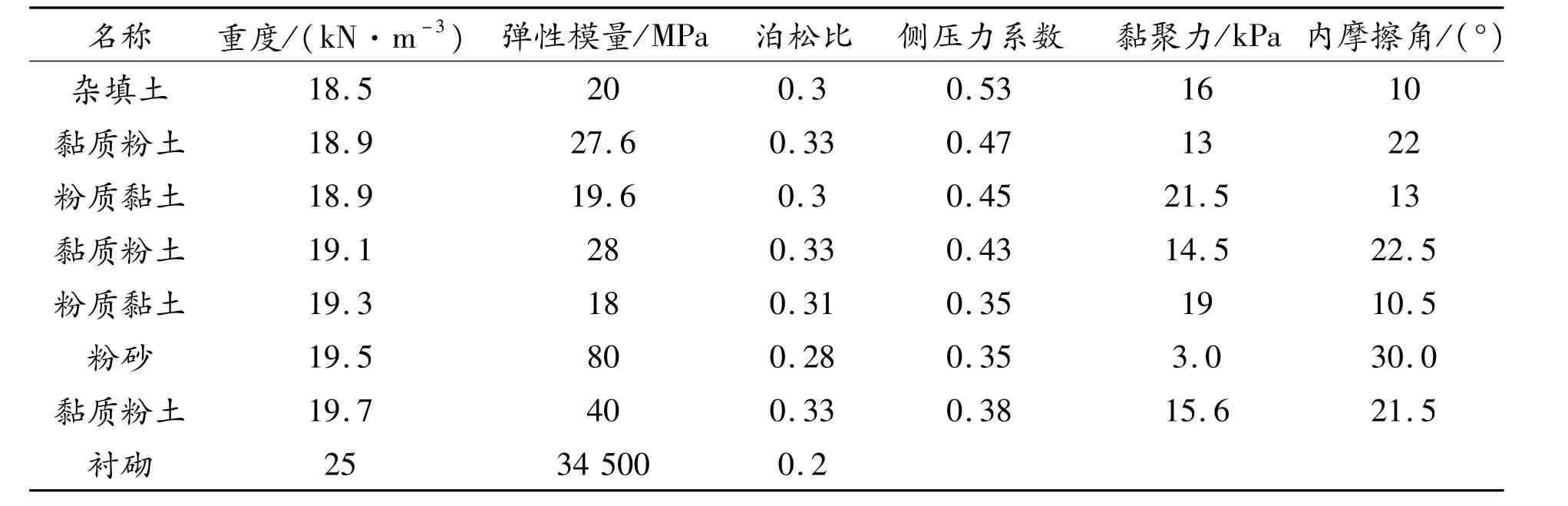
表1 土体各层物理力学与结构计算参数

2.2 有限元模型的建立

本文采用MIDAS／GTSNX有限元软件作为分析手段，建立地铁车辆－隧道－土体相互作用的三维有限元分析数值模型，并分析单车运行与双车交会两种工况下的隧道结构的动力响应［8］。建立的土体几何模型尺寸［9］为宽130 m、高60 m、长83 m。土体分层情况如图3所示。类矩形隧道结构处于粉砂层。模型土体采用摩尔库伦本构模型进行模拟。为保证计算结果的精确度，动力分析时施加黏性边界，并固定底部条件［10－11］。根据模型尺寸、特征值及地层力学参数设置相应的刚度与阻尼，模型分析时阻尼采用动力分析中常用的瑞利阻尼［12］。

2.3 列车荷载模拟

根据郑州地铁8号线情况，地铁车辆为A型车，列车采用4动2拖6辆编组，列车最大时速为100 km／h。为方便计算，设计行车速度为72 km／h（20 m／s），列车轴重为16 t，车轮静荷载为80 kN。本文采用24组轴荷载（160 kN）模拟郑州地铁8号线A型车车轮荷载。地铁列车运营速度为72 km／h的时程荷载曲线如图4所示［13］。

图4 列车荷载时程曲线

3 有限元模型分析

本文双车交会工况由两辆列车以72 km／h的速度分别从畅和街站和郑州东站相向而行并会车；单车运行工况由一辆车以72 km／h的速度从畅和街站往郑州东站方向行驶。根据隧道在空间分布中的结构特点，选择3个控制断面进行分析（见图5），其中断面2处于两车交会处。

图5 控制断面分布示意图

为了更好地分析类矩形隧道在地铁行车荷载下的影响，选取隧道断面衬砌外表面相应的点位进行分析［14］（见图2）。其中，节点A与节点C均在衬砌两侧中间位置，节点B在各断面中衬砌最底部位置，节点D与节点E均位于行驶列车正下方对应位置。

3.1 位移响应分析

图6为双车运行时类矩形隧道结构的竖向位移云图，其中图6（a）、图6（b）、图6（c）分别对应于两车驶入隧道、两车相遇、两车驶离等3种情况。由图6（b）可知，当t＝6.2 s时，两车相遇，此时最大竖向位移发生在隧道结构中部节点A与节点C的位置，为1.11 mm；由图6（c）可知，当t＝12.7 s时，两车驶离，此时最大竖向位移发生在隧道结构中段顶部位置，为0.000 5 mm。

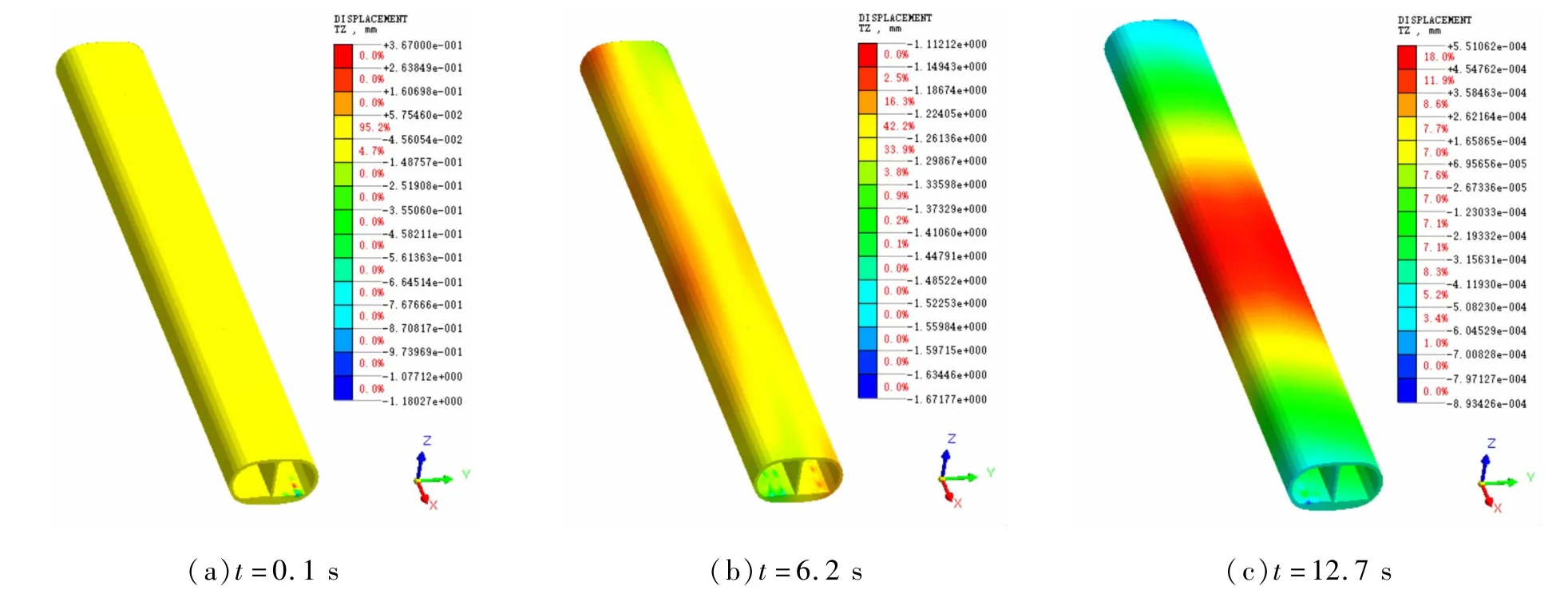
图6 双车运行时竖向位移云图

图7为断面1处与断面2处衬砌各点竖向位移时程曲线。单车运行与双车运行两种工况下，类矩形隧道衬砌随时间的位移变化规律基本一致，不同时间点的位移相差不大。

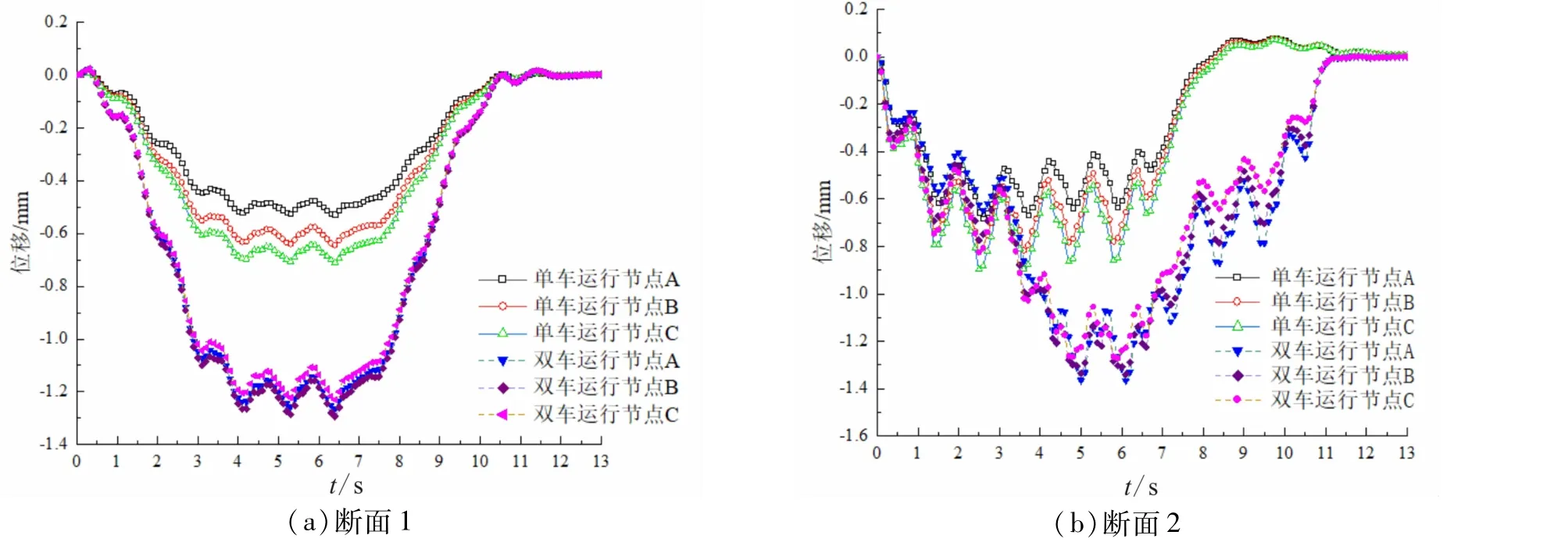
图7 断面处衬砌位移时程曲线

由图7（a）可知，在双车运行时，衬砌C点处的位移在3.9 s之前大于其余两个点位，而在3.9～4.8 s，衬砌底部B点处的位移值最大，在4.8 s之后，衬砌A点处的位移最大。由图7（b）可知，单车运行引起的位移最大值和最小值分别约为0.71 mm和0.52 mm；在列车交会时引起的位移最大值和最小值分别约为1.28 mm和1.22 mm，位移最大值在衬砌底部B点处。综上所述，地铁交会时会产生位移的瞬时局部变化，但是由此产生的位移小于两车单独引起的位移峰值的简单叠加。

3.2 隧道衬砌应力响应分析

图8与图9分别为双车运行时类矩形隧道结构竖向应力云图与轴向应力云图，由图9（c）可以看出，当t＝12.7 s时，两车驶离，类矩形隧道结构最大轴向应力发生在结构顶部，最大轴向应力为0.249 kPa。

图8 双车运行时竖向应力云图

图10和图11分别为断面2处衬砌的竖向与轴向的应力时程曲线。由图10（a）和图11（a）可知，在地铁单车行驶过程中，衬砌节点E处发生了应力振荡，竖向应力振荡幅值最大为2.5 kPa，轴向应力振荡幅值为49.6 kPa。同时，衬砌节点D处也发生了应力振荡，最大值为3.2 kPa，节点D处的应力变化曲线与E处的应力变化曲线相反，这是由于载荷的偏置导致的。在此期间，衬砌节点D处的轴向应力振荡幅度小于竖向应力振荡幅度，随着列车的行驶，振荡幅值缓慢减小。由图10（b）可知，双车交会运行时，衬砌节点D处在2.9 s时竖向应力幅值最大，为5.2 kPa。衬砌节点E处在7.8 s时竖向应力幅值最大，为4.1 kPa。节点D处的最大竖向应力值相较于节点E处增加了1.1 kPa，增幅约26.8%。由图11（b）可知，衬砌节点D与节点E处的轴向应力幅值差别很小并同步变化，最大值为62 kPa。分析图11可以看出，单车运营时节点E处轴向应力变化曲线与双车运行时节点E处轴向应力变化曲线变化幅度基本相同。综上所述，在双车交会运行与单车运行时对类矩形隧道结构两侧的影响并不相同。

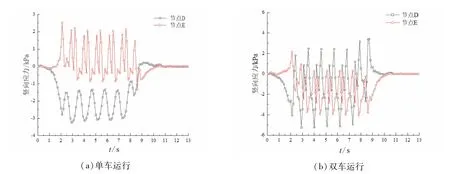
图10 断面2处衬砌竖向应力时程曲线

图11 断面2处衬砌轴向应力时程曲线

4 结论

以郑州地铁8号线畅和街站至郑州东站类矩形隧道段为背景，采用理论分析和数值模拟的研究方法，建立地铁列车荷载作用下类矩形隧道三维有限元分析数值模型，研究其在地铁列车荷载作用下的动力响应规律。主要结论如下：

（1）在列车双车相向运行时，所产生的隧道衬砌位移大于单车运行时所产生的位移，但不能通过单车运行时产生的位移进行简单叠加。地铁列车交会时最大位移发生在衬砌底部，为1.28 mm；单车运行时，最大位移发生在衬砌行车侧右边，不在衬砌底部，约为0.89 mm。

（2）在列车单车运行时，行驶车辆侧的竖向应力时程曲线与另一侧的竖向应力时程曲线相反，是由于载荷的偏置导致的。在双车相向行驶时，隧道衬砌左侧的竖向应力响应大于隧道衬砌右侧的竖向应力响应，增幅约为26.8%。隧道结构两侧的轴向应力同步变化，差别较小。在运营期，应主要关注隧道结构左侧行车线下方的竖向应力响应情况，以避免在此处发生结构安全问题。