基于第一着枝角度的罗田垂枝杉树冠表面积预估模型研究

莫 嬃，易 烜，边更战，陈书杭

(1.中南林业科技大学，湖南 长沙 410004；2.湖南省青羊湖国有林场，湖南 长沙 410600；3.中部林业产权交易服务中心，湖南 长沙 410007；4.咸宁市林业科学院，湖北 咸宁 437000)

树冠是树木的重要组成部分，是树木生长与生理过程的主要部位[1]。树冠的大小能够体现树木的生长潜力以及竞争能力，也是预估树木生长量的基本依据之一[2]。树冠三维空间的大小通常用树冠表面积和树冠体积表示[3-7]。树冠表面积、体积等复合指标不仅与林木生长和健康有着密切的关系，而且能用其构建生长空间竞争指数和生长空间指数[8-10]，因此，研究树冠表面积对进一步分析和优化调整林分的空间结构具有重要意义。目前，对于树冠表面积量化方面的研究仍然存在许多挑战[11]。传统的树冠表面积测量方法通常需要大量的人工测量和复杂的数据处理，需要消耗大量的人力、物力和财力[12]。几何体法是常用的树冠表面积计算方法，即将树冠近似看作圆锥体进行计算[13]。早在1969年，Hamilton[14]对西特喀云杉(Stikaspruce)进行了研究，在计算时将树冠看成圆锥体很容易得出树冠的表面积。近年来，涂宏涛等[15]、吴明钦等[16]在构建树冠表面积模型时，为使得到的数据更加精确，常常将几何体法与平均断面求积法结合起来，也称其为“分层切割法”。由于树冠结构的复杂性，很难对树冠表面积进行准确的测算[17]，因此，在需要使用新方法测算树冠表面积时，常常用“分层切割法”计算的值作为对照，以评判新方法的准确性和可信度[18]。值得一提的是，不论是几何体法还是分层切割法，其本质都是将树冠看作与其相近的几何体，再进行拆解、估算。而在这两种树冠表面积测算法中，对于树冠下层侧枝的着枝状态都未曾引起重视。我们以罗田垂枝杉(Cunninghamialanceolatavar.luotian)为研究对象[19-21]，建立适用于该树种的树冠表面积预估模型，为其经营管理提供参考。

1 研究区概况

罗田垂枝杉试验林于2016年初造林，其造林密度为1.5m×1.5m，位于湖北省咸宁市东南部的贺胜桥镇。该镇地处114°16′—114°29′E，29°57′ — 30°02′N，其东西长31.5km，南北宽10.1km，最高山脉海拔264m，东部为丘陵岗地，西部为平原湖区，地形东高西低，由东南向西北呈现为高丘、丘岗、平湖。研究区气候属典型的亚热带季风气候，冬冷夏凉，四季分明，光照充足，雨量充沛。冬季盛行偏北风，偏冷干燥；夏季盛行偏南风，高温多雨。年平均气温16.8℃，极端最高气温41.4℃，极端最低气温-15.4℃。年平均降水量1577.4mm，年平均日照时数1754.5h，年平均无霜期245～258d[22]。

2 研究方法

2.1 数据采集

2023年4—5月，在湖北省咸宁市贺胜桥镇的垂枝杉试验林随机设置30块15m×20m的标准地，并对标准地内的林木进行每木检尺，调查记录胸径(D)、树高(H)、活枝下高(HCB)、冠幅(CW)、冠长(CL)等测树因子，然后根据林分平均胸径在每块标准地内选取2～3株平均木作为标准木，共选取71株标准木。将标准木伐倒后，采用分层切割法将树冠按1 m的长度分层，每层内选取3～5个标准枝作为样枝测量枝长及其着枝角度。标准木主要测树因子调查数据统计结果见表1。

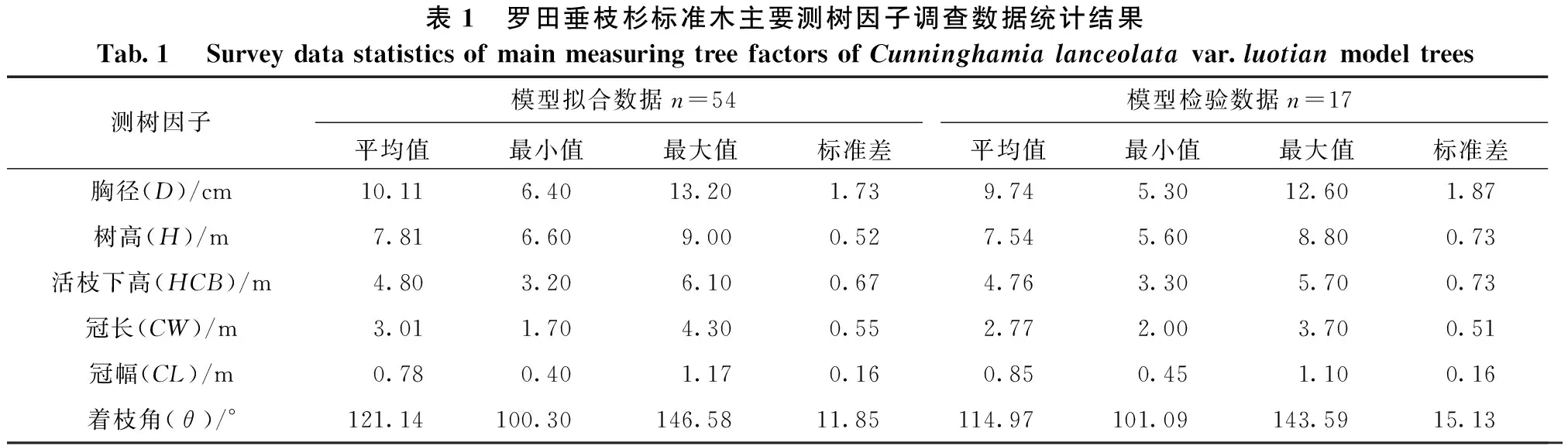
表1 罗田垂枝杉标准木主要测树因子调查数据统计结果Tab.1Survey data statistics of main measuring tree factors of Cunninghamia lanceolata var.luotian model trees测树因子模型拟合数据n=54模型检验数据n=17平均值最小值最大值标准差平均值最小值最大值标准差胸径(D)/cm10.116.4013.201.739.745.3012.601.87树高(H)/m7.816.609.000.527.545.608.800.73活枝下高(HCB)/m4.803.206.100.674.763.305.700.73冠长(CW)/m3.011.704.300.552.772.003.700.51冠幅(CL)/m0.780.401.170.160.850.451.100.16着枝角(θ)/°121.14100.30146.5811.85114.97101.09143.5915.13

2.2 树冠表面积计算

采用分层切割法计算树冠表面积[14]，即将罗田垂枝杉的树冠按1 m长度分成若干层，将其树冠底部至中部每层视为圆台体，将最顶层视为圆锥体；分别计算每个冠层的平均枝长，再根据枝长(L)与着枝角度(B)之间的三角函数关系计算每个冠层的顶部和底部半径(C)。

C=BLsinθ

(1)

用圆台体、圆锥体表面积计算公式计算树冠各层表面积，累加树冠各层表面积得到全树冠表面积。

(2)

(3)

式中：h为冠层长度；CR为冠层底部半径；Cr为冠层顶部半径。

2.3 树冠表面积预估模型建立

2.3.1 模型结构设计

根据实测所得的71株标准木调查数据，建模数据与模型检验数据按约3∶1的比例随机抽取，抽取其中54株标准木的解析数据作为建模数据，剩余17株标准木的解析数据作为模型检验数据。相关研究表明，异速生长方程(式4)能够很好地拟合树冠表面积模型[23]。并运用R 4.3.1软件进行回归分析，建立预估方程。

(4)

式中：y为树冠表面积；x1、x2、xi均为林木测树因子变量；a、b、c、d均为待估参数。

2.3.2 模型变量筛选

根据实测数据，将测树因子变量与树冠表面积进行 Pearson 相关性分析[24]，结果见表2。由表2可知：胸径、树高、冠长、冠幅与树冠表面积的相关性均达显著或极显著，其中树冠表面积与冠幅的相关系数最大；活枝下高与树冠表面积的相关系数最小。

表2 树冠表面积与标准木测树因子变量的Pearson相关性分析结果Tab.2 Pearson relation analysis between main measuring tree dendrometry factor variables and crown surface area变量胸径树高冠长冠幅活枝下高树冠表面积0.779**0.377**0.756**0.839**-2.81* 注:*表示相关显著(P<0.05); **表示相关极显著(P<0.01)。

2.3.3 模型评价与检验

对建模样本进行检验，计算检验指标，评价模型优度。使用确定系数(R2)、精度(EA)、剩余标准差(S)、平均相对误差(E)和平均相对误差绝对值(e)[15]对备选模型进行检验，选取最优模型。其中，R2、EA越接近1越好；S、E、e越接近0越好。

(5)

(6)

(7)

(8)

(9)

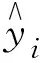
3 结果与分析

3.1 基于第一着枝角度的单木树冠表面积计算

3.1.1 传统几何体法

几何体法是计算树冠表面积的传统方法，即将树冠近似看作圆锥体进行估算，其计算公式为式(10)。通常我们在使用几何体法计算树冠表面积时，对于冠长(圆锥体的高)的定义为树冠顶部到第一活枝着枝点的垂直长度，即树高与枝下高之差(CL=H-HCB)。其树冠结构示意图见图1。

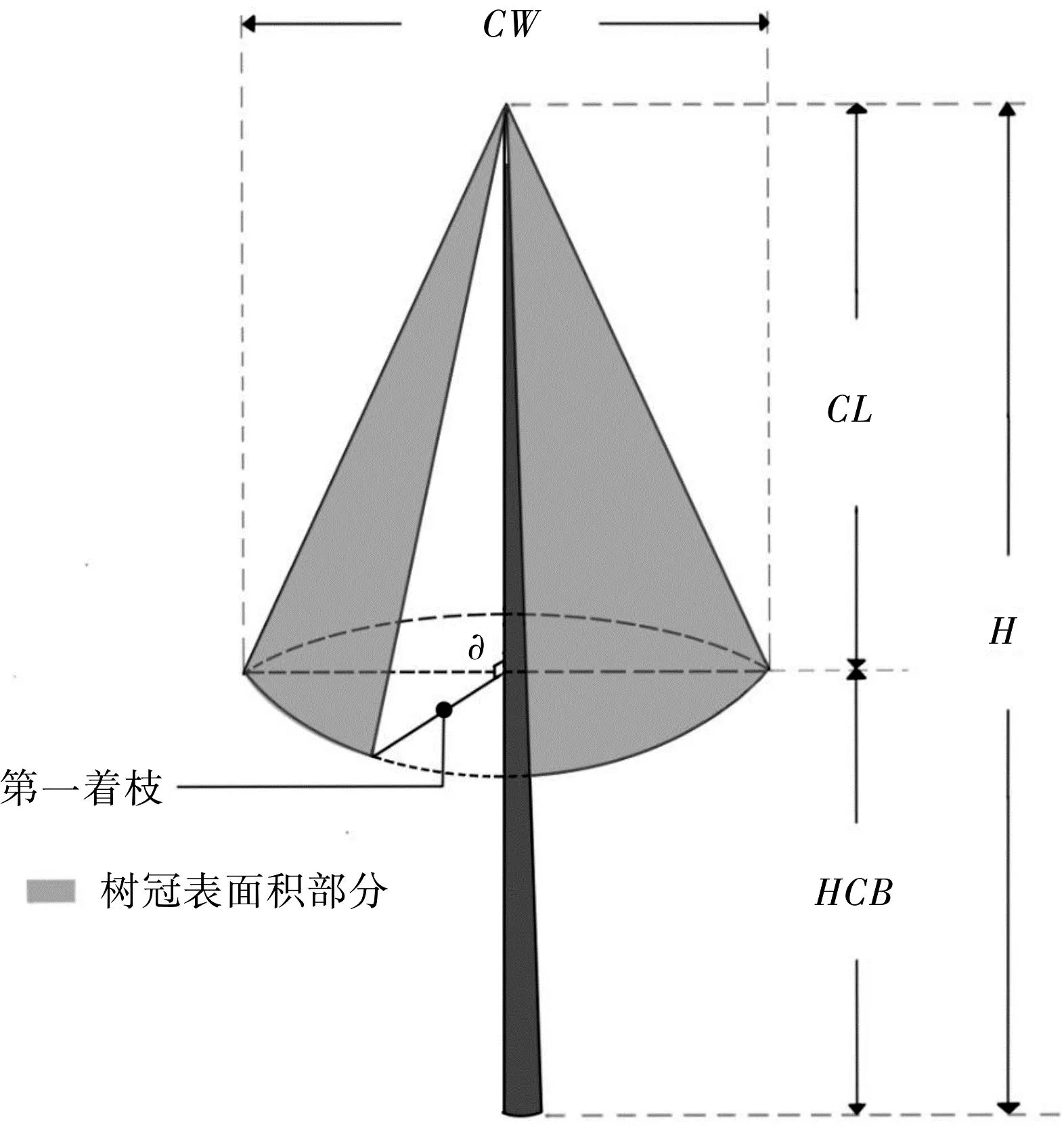
图1 几何体法树冠结构示意图Fig.1 Schematicdiagram of tree crown structure using geometric method

当∂=90°时，树冠表面积传统几何体法的计算公式为：

(10)

(11)

式中：CSAi为第i株木的树冠表面积；CWi为第i株木的冠幅；CLi为第i株木的冠长；CWewi、CWsni分别为第i株木的东西、南北冠幅。冠长(CLi)为树高与枝下高之差。

3.1.2 基于第一着枝角度的几何体法

罗田垂枝杉与普通杉木相比有着十分显著的形态差异，其侧枝自然下垂，树冠下层侧枝着生角度达150°左右。因此，其冠长若仍以树高与枝下高之差值来定义，在使用传统几何体法计算时得到的表面积将与实际表面积存在误差，其误差如图2所示。

图2 几何体法计算得到的罗田垂枝杉树冠表面积与其实际表面积的误差示意图Fig.2 Schematic diagram of the error betweenthe surface area of Cunninghamia lanceolata var.luotian tree crown calculated by the geometric method and its actual surface area

由图2可知，在第一着枝角度∂的影响下，垂枝杉冠底与着枝点在垂直方向上存在差值Δcl，与着枝角度∂的关系为：

(12)

因此，垂枝杉实际冠长为传统冠长与ΔCL之和，即CL+ΔCL。由此可推算出适用于在∂>90°时罗田垂枝杉树冠表面积的几何体法计算公式为：

(13)

式中：CSAj为第j株木的树冠表面积；CWj为第j株木的冠幅；CLj为第j株木的冠长；冠长(CLj)为树高与枝下高之差。

3.2 第一着枝角度对树冠表面积预估精度的影响

3.2.1 树冠表面积不同计算方法的精度比较

利用实测得到的71株垂枝杉标准木调查数据，分别使用传统几何体法、基于第一着枝角度的几何体法以及分层切割法计算垂枝杉树冠的表面积，结果见表3。由表3可知，树冠表面积的平均值、最大值、最小值和标准差都是分层切割法的>基于第一着枝角度的几何体法的>传统几何体法的。

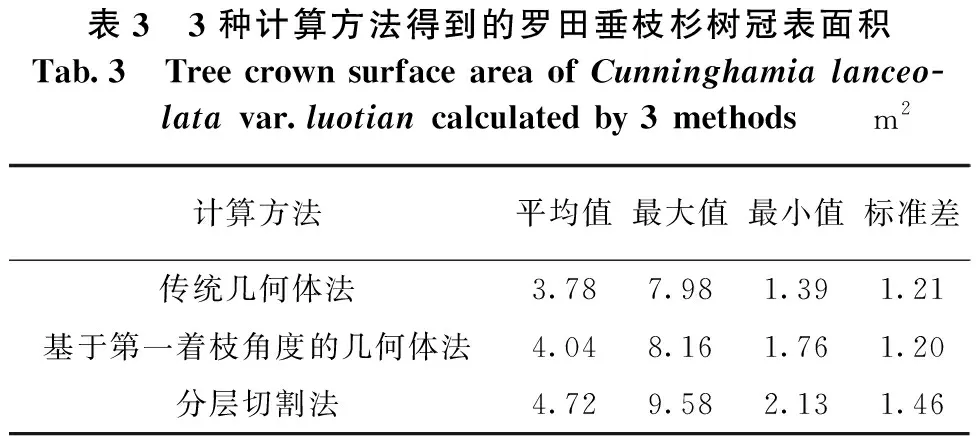
表3 3种计算方法得到的罗田垂枝杉树冠表面积Tab.3Tree crown surface area of Cunninghamia lanceo-lata var.luotian calculated by 3 methodsm2计算方法平均值最大值最小值标准差传统几何体法3.787.981.391.21基于第一着枝角度的几何体法4.048.161.761.20分层切割法4.729.582.131.46

由于垂枝杉树冠形态的不规则性以及实际操作的困难性，目前无法获取其树冠的实际表面积。为比较传统几何体法与基于第一着枝角度的几何体法的计算精度，以分层切割法得出的表面积作为参照，将分层切割法、传统几何体法与基于第一着枝角度的几何体法计算得出的树冠表面积绘制成图3。图3结果表明，分层切割法得出的表面积最大，基于第一着枝角度的几何体法得出的次之，传统几何体法得出的最小。可见，基于第一着枝角度的几何体法得出的树冠表面积较传统几何体法得出的更加接近分层切割法得出的，说明对于垂枝杉而言，基于第一着枝角度的几何体法得出的树冠表面积较传统几何体法得出的更加准确。

图3 3种方法计算得出的树冠表面积(小提琴图与箱线图)Fig.3 Crown surface area calculated by three methodes(violin chart and box chart)

3.2.2 树冠表面积与第一着枝角度的相关性

树冠第一着枝角度是树冠表面积大小的决定性因素之一。将第一着枝角度大于90°的部分，即第一着枝角与垂直角的差值，和与其对应带来的表面积差值绘制成散点图(图4)。由图4可知，第一着枝角度差与树冠表面积差没有明显的线性关系。在树冠表面积的相关测树因子一致的前提下，继续绘制角度差与表面积差的散点图。

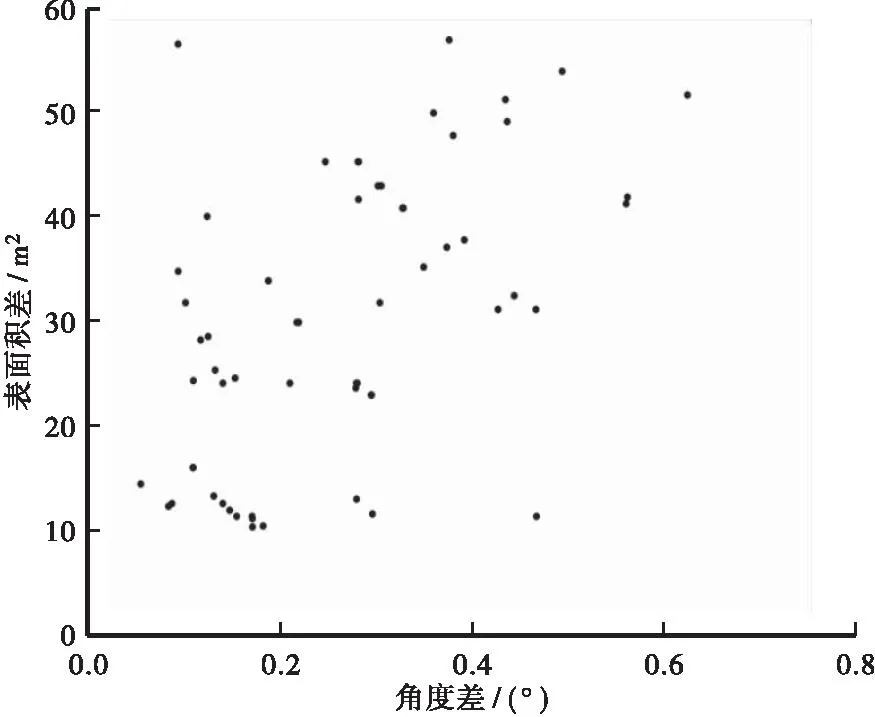
图4 角度差与表面积差的散点图Fig.4 Scatter plot of angle difference versus surface area difference

先考虑冠幅一致时第一着枝角度与树冠表面积的关系。选取冠幅为0.7 m的9株标准木，绘制第一着枝角度差与树冠表面积差的散点图(图5a)。由图5a可知，在冠幅相同的情况下，角度差越大表面积差也越大，即第一着枝角度的大小与树冠表面积的大小呈正相关。

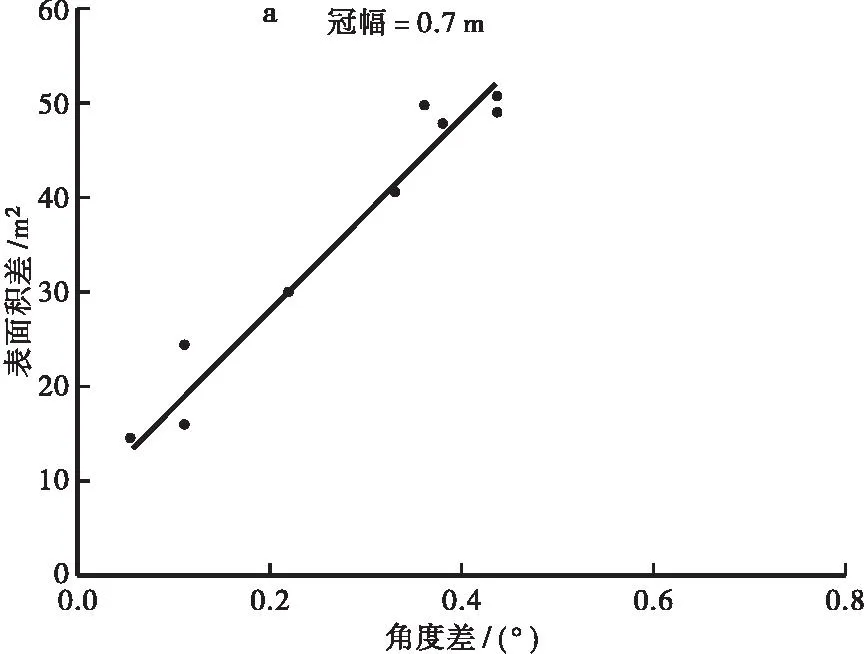
再考虑冠长相同时第一着枝角度与树冠表面积的关系。选取冠长为3.1 m的9株标准木，绘制第一着枝角度差与树冠表面积差的散点图(图5b)。由图5b可知，在冠长相同的情况下，角度差越大表面积差也越大，说明第一着枝角度大小与树冠表面积的大小也呈正相关。

3.3 罗田垂枝杉树冠表面积预估模型构建

以建模数据拟合树冠表面积预估模型。先引入单变量胸径(D)拟合为一元变量模型，再分别引入冠幅(CW)、冠长(CL)拟合为二元变量模型，然后用3个变量拟合成三元变量模型，最后分别选取3种拟合模型中R2(拟合优度或判断系数)、EA精度(精度)最大的模型，并计算参数估计值、评价指标值。拟合结果见表4。由表4可知：随着模型变量的增加，模型方程的R2(拟合优度或判断系数)不断增大，EA也一直呈增加趋势，说明模型的精度不断提高。其中一元变量模型的拟合优度和精度均最低，分别为0.62和81.99%；三元变量模型的均最大，分别为0.98、96.89%；在二元变量模型中，模型3的R2和EA均较大。考虑到实际调查中数据获取的难易程度，选取模型3和模型4为备选模型。

表4 罗田垂枝杉树冠表面积模型拟合结果Tab.4 Fitting results of crown surface area model for Cunninghamia lanceolata var.luotian模型编号变量参数估计评价指标abcdR2EA/%1D0.191.410.6281.992D、CW1.390.630.870.7786.093D、CL1.010.810.830.8187.144D、CW、CL1.970.070.940.870.9896.89

模型3、4的表达式如下。

模型3：CSA=1.01D0.81CL0.83

(14)

模型4：CSA=1.97D0.07CW0.94CL0.87

(15)

以模型检验数据对模型3、4进行检验，检验结果如表5所示。表5结果显示：在2个树冠表面积备选模型中，以模型4为优，其预估精度EA达96.95%，平均相对误差E仅为0.01；模型3的预估精度EA也达到了80%以上，且平均相对误差E为0.56，因此，2个备选模型都能较好的预估罗田垂枝杉的树冠表面积。

表5 罗田垂枝杉树冠表面积模型检验结果Tab.5Test results of crown surface area model for Cun-ninghamia lanceolata var.luotian模型编号方程变量评价指标R2EA/%SeE3D,CL0.7484.622.200.680.564D,CW,CL0.9896.950.620.130.01

4 结论与讨论

(1)3种计算方法得到的罗田垂枝杉树冠表面积的大小为分层切割法的>基于第一着枝角度的几何体法的>传统几何体法的，表明以分层切割法作为参照时，基于第一着枝角度的几何体法计算树冠表面积的精度高于传统几何体法的，也进一步验证了第一着枝角度是树冠表面积的决定性因素之一。

(2)罗田垂枝杉树冠表面积与胸径、冠长、冠幅等均呈显著正相关，其中与冠幅的相关系数最高；异速生长方程能很好地拟合树冠表面积模型，测树因子变量的增加能适当地提高模型拟合的精度。其中以胸径、冠长以及冠幅为变量的三元变量模型来拟合树冠表面积的模型为最优模型，模型的判断系数R2达0.98，模型的精度EA也达到了96.95%，说明所建立的模型具有较高的估测精度，其模型为CSA=1.97D0.07CW0.94CL0.87。

(3)在针对树冠体积、表面积估测模型的研究中[25]，林木的胸径、冠幅等测树因子都还需要通过实测手段来获取数据，并寻求与树冠形态相近的表面积、体积公式进行计算，这种计算方式无疑过于粗放。随着科学技术的发展，林业资源调查已不仅仅局限于传统方式。如利用地面三维激光扫描技术对建模样木进行不同方向的扫描来拟合获得整株林木的完整点云数据，再通过数据处理生成树冠的三维点云模型[26]；还有通过无人机倾斜摄影测量，对树木的模型进行三维重建，从而得到树冠表面积与体积[27]。显然，因为新科技产生了新方法，使计算出的树冠表面积、体积都更加精确，且大大节省了人力、物力。

(4)本文在计算树冠表面积时考虑了树冠第一着枝角度，其表面积的计算更具灵活性。罗田垂枝杉的树冠第一着枝角度大于90°，而在自然界中不乏枝条与地面反向生长的树种，即树冠第一着枝角度小于90°，对于此类型树种树冠表面积与第一着枝角度的关系，也有待进一步研究。