一种低电压应力和电感电流纹波的准Z源逆变器调制策略

易文静，罗超逵，罗朝旭，程谆

(1．湖南工业大学电气与信息工程学院，湖南 株洲 412007；2.贵州电网有限责任公司凯里供电局，贵州 凯里 556099；3.湖南铁道职业技术学院，湖南 株洲 412001)

0 引言

传统电压源逆变器为降压型变换器，在输入电压较低或宽变化范围的场合下，需要在前级加升压变换器，这种两级功率变换器通常会导致系统结构更复杂、成本更高且效率变低[1-4]。Z源逆变器可以克服上述不足，与传统的电压源相比，Z源逆变器通过在输入端和逆变桥中加入Z源阻抗网络，实现单级升降压逆变器功能，使得系统结构简单且成本更低[5-6]。但Z源逆变器仍存在输入电流不连续、功率器件电压应力高，以及输入电源与负载之间没有公共接地等缺点[7-8]。因此，在Z源逆变器基础上提出了两种准Z源逆变器，这两种准Z源逆变器都有着公共接地的优点，区别在于是否有连续的输入电流[9-10]。

尽管输入电流连续的准Z源逆变器有很多优势，但其功率器件和准Z源网络中电容的电压应力仍然很高，同时准Z源网络电感电流纹波较高。很多研究通过在准Z源逆变器选用高速开关器件来降低电感电流纹波，例如SiC-MOSFET、GaN-HENT和SJ-MOSFET[11-13]。然而，这种方法必须在增加器件开关损耗和降低电感电流纹波之间进行权衡。此外，这种方法的有效性很大程度上取决于电路结构[14]和器件的开关性能[15]。同时，改变调制策略减少电感器电流纹波也十分有效，并且不受电路结构和器件的开关性能的约束。正弦脉冲宽度调制(sinusoidal pulse width modulation，SPWM)[16]策略和空间矢量脉冲宽度调制(space vector pulse width modulation，SVPWM)[17]策略是三相准Z源逆变器实现上下桥臂直通最常用的两大类调制策略。SPWM策略中最常见的有简单升压调制(simple boost control，SBC)[18]策略、最大升压调制(maximum boost control，MBC)[19]策略和最大恒定升压调制(constant boost control，CBC)[20]策略。简单升压调制策略作为最常用的调制策略实现简单，计算量小，但存在高电感电流纹波和功率器件承受电压应力高的缺陷；为了降低SBC策略中的高电压应力，MBC策略被提出，但这种方法给电感电流带来了低频脉动。而CBC策略在降低电感电流纹波的同时不引入低频脉动，但较窄的调制度范围使其仍有较高的开关电压应力。SVPWM策略与SPWM策略相比，增大了调制度的变化范围，在一定程度上减少了功率器件的电压应力，但实现起来系统结构更为复杂，计算量变大，系统运行时间明显变长[21]。文献[22]提出了一种优化直通时间的SVPWM策略，在一定程度上降低了电感电流纹波，但是计算变得更加复杂，且并未优化系统的电压应力。

本文基于简单升压控制提出一种注入均值信号的调制策略，均值信号为三相正弦调制波最大值和最小值的均值。通过将均值信号注入三相正弦调制波中从而得到新的调制波，再用新的调制波对准Z源逆变器进行控制完成升压逆变的功能。与简单升压控制相比，新的调制策略在减小功率器件和电容电压应力的同时，有效降低电感电流纹波脉动，有着更优良的综合性能。

1 三相准Z源逆变器工作原理和简 单升压调制策略

三相准Z源逆变器拓扑如图1所示，准Z源阻抗网络由电感L1、L2、电容C1、C2和二极管D构成。分析准Z源逆变器工作原理时准Z源阻抗网络对称，即L1=L2，C1=C2。准Z源逆变器在一个开关周期中有两种工作模式，分别为直通模式和非直通模式。这两种工作模式的等效电路分别如图2(a)、(b)所示。

图1 三相准Z源逆变器拓扑

(a)直通状态

(b)非直通状态

准Z源逆变器直通时，电感充电，电容放电，有：

vL1=VC2+Vin

(1)

vL2=VC1

(2)

处于非直通状态时：

Vin=vL1+VC1

(3)

vL2=-VC2

(4)

综合式(1)—(4)和电感电压的伏秒平衡原理可得电容电压VC、直流链峰值电压Vpn分别为：

(5)

(6)

式中：T是一个开关周期的时间；T0为一个开关周期内直通零矢量持续的时间；D0为直通占空比；B定义为升压因子。式中直流侧电压仅表示电路工作在非直通状态时的值。

准Z源逆变器的工作状态不同于传统电压型逆变器的工作状态，准Z源逆变器需要在传统8个基本工作状态中添加直通零矢量工作状态，添加直通零矢量之后传统的调制策略可适用于准Z源逆变器。简单升压调制策略是常用SPWM策略中最简单的一种，参考信号和逆变桥开关信号如图3所示。

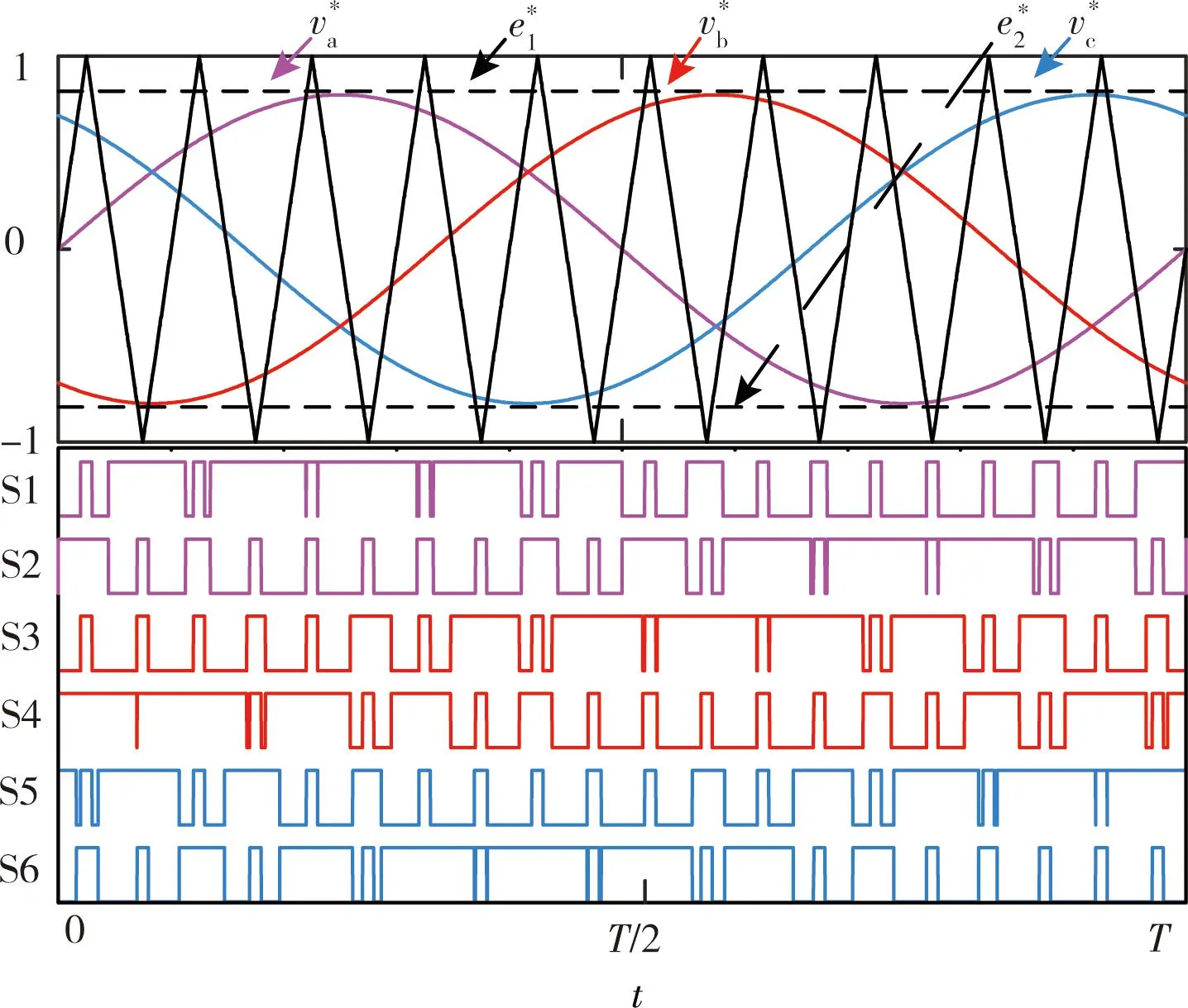
图3 一个周期的简单升压调制示意图

为了更直观地展示调制过程，载波比设置为10。定义调制因数m为三相正弦调制波峰值Vts与三角载波峰值Vtc之比，则m被限制在0≤m≤1。设简单升压控制下的三相正弦调制信号为：

(7)

(8)

简单升压控制下的升压因子B、电压增益G和输出相电压峰值vp分别为：

(9)

(10)

(11)

2 注入均值信号调制策略

本文提出的注入均值信号调制策略的实现不同于简单升压调制策略，不需要额外的参考信号，通过向三相正弦调制信号注入均值信号就能实现逆变桥的直通，同时获得低电压应力和电感电流纹波的特性，图4为控制示意图。

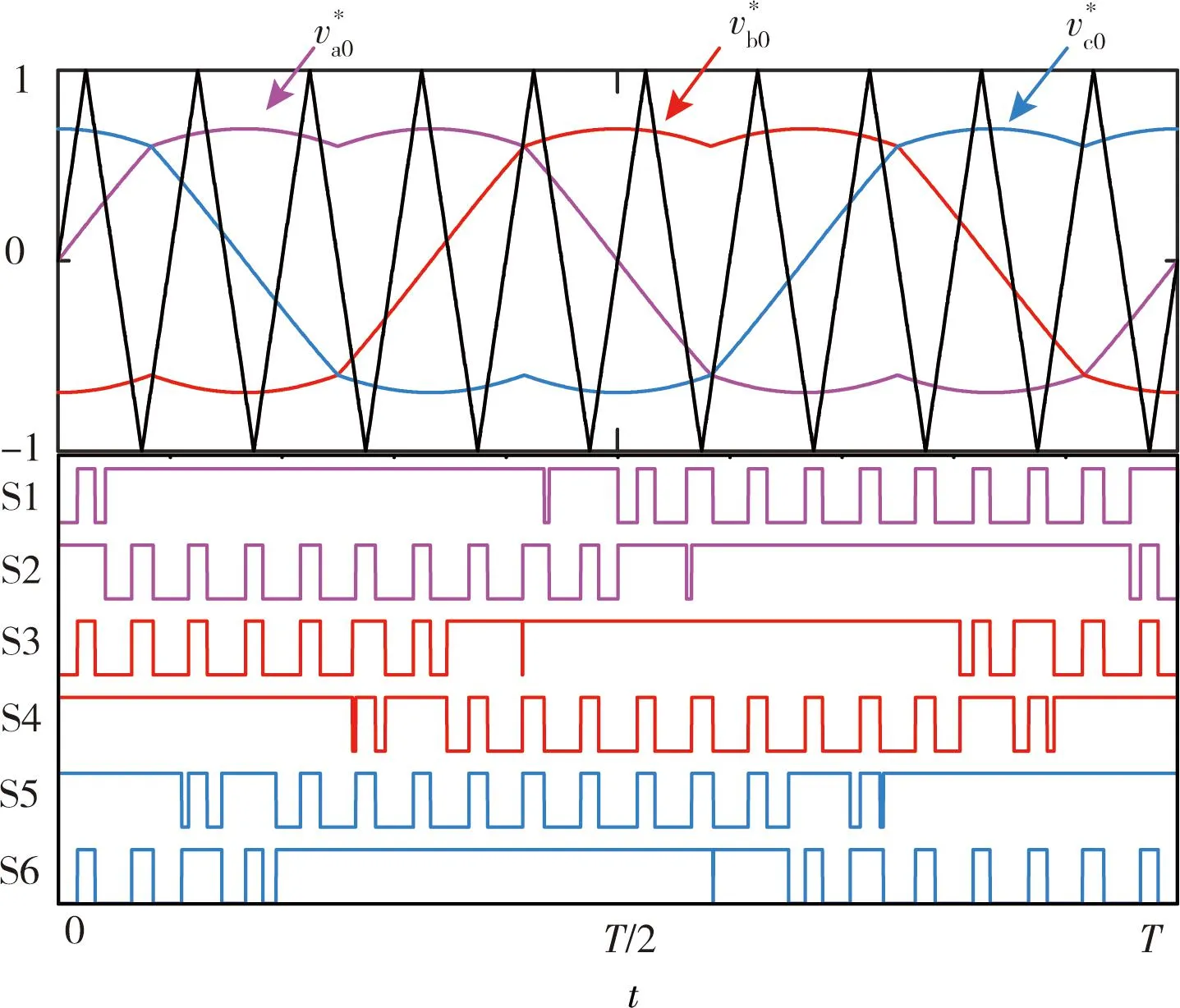
图4 一个周期的注入均值信号调制策略示意图

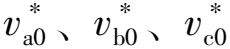
(12)

则均值信号v0定义为：

(13)

(14)

对于提出的注入均值信号调制策略，直通占空比D0以π/6为周期变化，用t0(θ)表示直通零矢量总的时间，直通占空比在(0，π/6)内可以表达为：

(15)

(16)

于是升压因子B为：

(17)

直流链电压Vpn可表示为：

(18)

电压增益G可由下式计算得到：

(19)

则输出相电压峰值vp为：

(20)

图5为简单升压控制和均值注入调制策略下电压增益G和调制度m的关系示意图。从图可知，注入均值分量后，调制度的范围更宽，同时在同一调制因数下，逆变器能获得更大的电压增益。

图5 调制因数与电压增益的关系

3 两种调制策略比较分析

3.1 电压应力比较分析

简单升压控制和均值注入控制策略下的逆变桥功率器件电压应力Vs、电容电压和电压增益G的关系如下。

1)简单升压控制：

Vs=(2G-1)Vin

(21)

VC1=GVin

(22)

VC2=(G-1)Vin

(23)

2)均值注入调制策略：

(24)

(25)

(26)

故，在相同电压增益G和输入电压Vin情况下，选取均值注入调制策略时，逆变桥开关器件的电压应力减少为：

(27)

与此同时，电容电压减小了：

(28)

图6和图7分别是两种调制策略下电压增益G与升压因子B和电容电压系数VC/Vin的关系示意图。由图可知，在同一电压增益G下，注入均值信号之后可使准Z源逆变器逆变桥功率器件和电容的电压应力均降低。

图6 升压因子B与电压增益G的关系

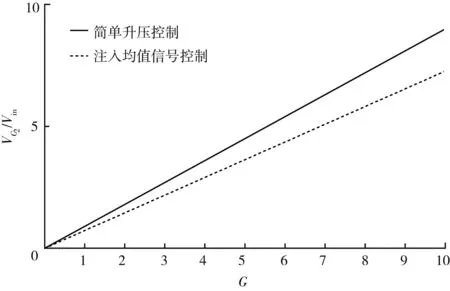
(b)电容C2的电容电压系数

3.2 电感电流脉动比较分析

准Z源逆变器工作在直通状态时，电感电流可由下式计算：

(29)

工作在非直通状态下电感电流为：

(30)

由式(29)和(30)可知，电感L1和L2取值相同时两个电感电流相同，故取L1=L2，此时准Z源逆变器的电感电流脉动为：

(31)

在给定电压增益G时，准Z源逆变器采用简单升压控制策略下的电感电流纹波为：

(32)

而采用均值分量注入后的电感电流纹波为：

(33)

(34)

式中：k1、k2分别为两种调制策略下的电感电流纹波系数。

图8为准Z源逆变器在同一输入电压时k1、k2与电压增益G的关系曲线，从图可以看出，在电压增益相同时，注入均值分量后的控制策略对应的电感电流纹波系数小于简单升压控制策略的电感电流纹波系数，且随着电压增益的增大，系数的差值变得越大。

图8 输入电压一定时电感电流纹波系数与电压增益G的关系曲线

当准Z源逆变器负载端相电压峰值vp一定时，由式(31)可知简单升压控制的电感电流纹波为：

(35)

采用均值注入调制策略的电感电流纹波可表示为：

(36)

其中，k3、k4的表达式为：

(37)

k3、k4和电压增益G的关系如图9所示，由图可知，当输出电压一定时，相同电压增益条件下，简单升压调制策略给准Z源网络电感带来的电感电流纹波更大，而注入均值分量之后系统电感电流纹波更小。

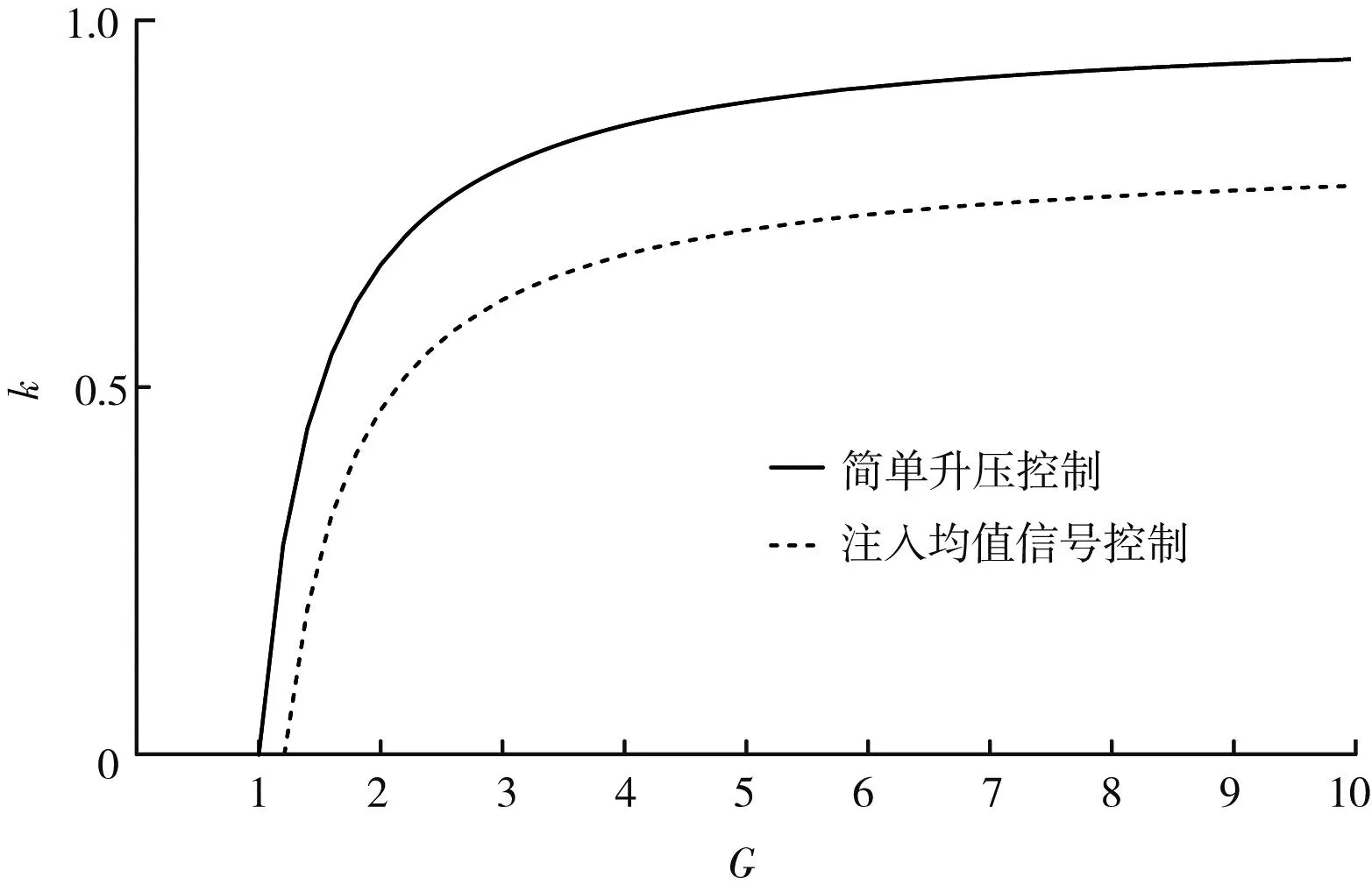
图9 同输出电压下电感电流纹波系数与电压增益G的关系曲线

3.3 直流链电压利用率比较分析

直流链电压利用率定义为线电压基波幅值与直流链电压之比。

简单升压控制策略下逆变器输出A、B相相电压可以表示为：

(38)

则输出线电压基波幅UAB为：

(39)

由此可知调制度为1时，采用简单升压控制策略下直流链电压利用率为0.866。

均值注入调制策略下逆变器输出A、B相相电压可以表示为：

(40)

则输出线电压基波幅UAB为：

(41)

由上述分析可知，相较于简单升压控制，注入均值信号控制可以得到更宽范围的调制因数m和更高的直流链电压利用率，开关器件电压应力更小，两个电容承受的电压更小；在相同的开关频率下，准Z源逆变器的电感电流纹波会减小，这有利于减少电感值从而减小逆变器体积。

4 仿真分析

为了验证前述分析，通过MATLAB/Simulink对准Z源逆变器在简单升压调制策略和注入均值信号调制策略这两种调制策略下进行仿真对比。设置仿真参数：令输入电压Vin=500 V，准Z源网络电感L1=L2=5 mH，电容C1=C2=1 000 μF，载波频率fs=10 kHz，负载R=15 Ω。图10为准Z源逆变器分别采用两种调制策略下的直流链电压Vpn，电容电压VC1、VC2，电感电流iL和输出相电压Vp的波形。

由图10可知，在同输入功率和同输出电压的情况下，两种调制策略下的平均电感电流相同，为25.5 A。与此同时，简单升压控制下的准Z源逆变器直流链电压约为1 030 V，采用注入均值分量后的调制策略直流链电压降低到765.5 V，直流链电压减少了约25.67%。与此同时，注入均值分量后电容电压VC1、VC2分别为632.3 V和132.2 V，而简单升压控制下的对应的两个电容电压分别为762 V和264 V，注入均值分量后电容承受的电压应力更低，可以有效减少电容体积和整个系统的重量。

两种调制策略下对应逆变桥功率器件电压应力Vsw和电感电流iL的局部放大图如图11所示。由图可知，逆变桥功率器件承受的电压应力数值与直流链电压值相同，则与简单升压调制策略相比，注入均值分量后逆变器功率器件电压应力减少了25.67%。此外，简单升压控制策略下的最大电感电流纹波为1.973 A，而注入均值分量之后准Z源网络的最大电感电流纹波减少到1.030 A，降低了约47.8%。由此可以看出，注入均值分量控制策略在达到相同效果下可以降低准Z源系统的最大电感电流纹波，有效减小电感成本。

(a)简单升压控制策略

(b)均值信号注入后的控制策略

(a)简单升压控制策略

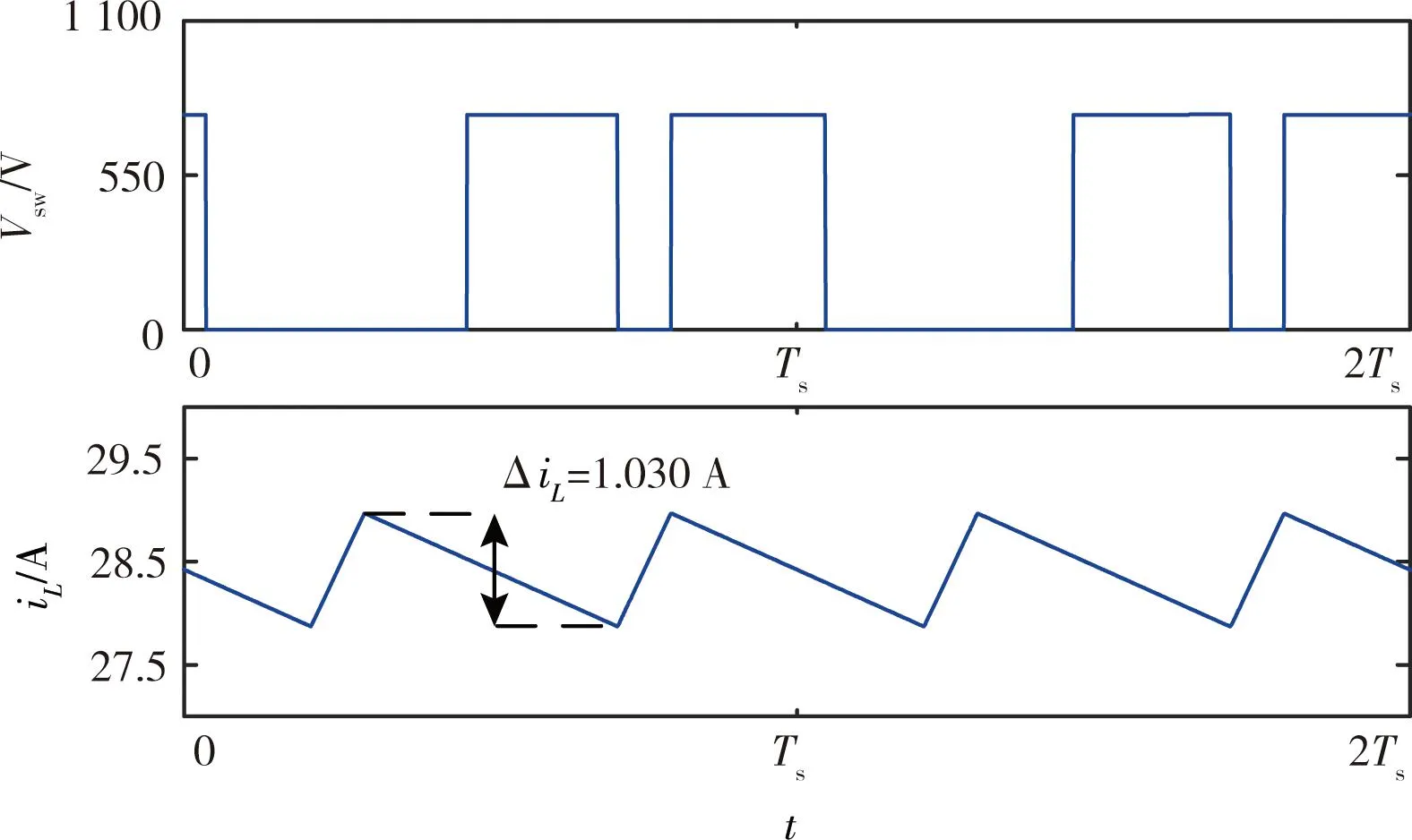
(b)均值信号注入后的控制策略

5 实验结果

使用RT-LAB实验平台进一步验证所提调制策略带来的低电压应力和电感电流纹波效果，DSP控制器选用TMS320F2812型号，三相准Z源逆变器系统由RT-LAB(OP5600)构建，系统参数与仿真参数保持一致。

图12为传统简单升压调制策略和所提出的均值信号注入调制策略方法的输出电压Vp和准Z源网络电感电流iL波形。由此可知，同输入功率和同输入电压情况下，两种调制策略对负载作用效果一致。

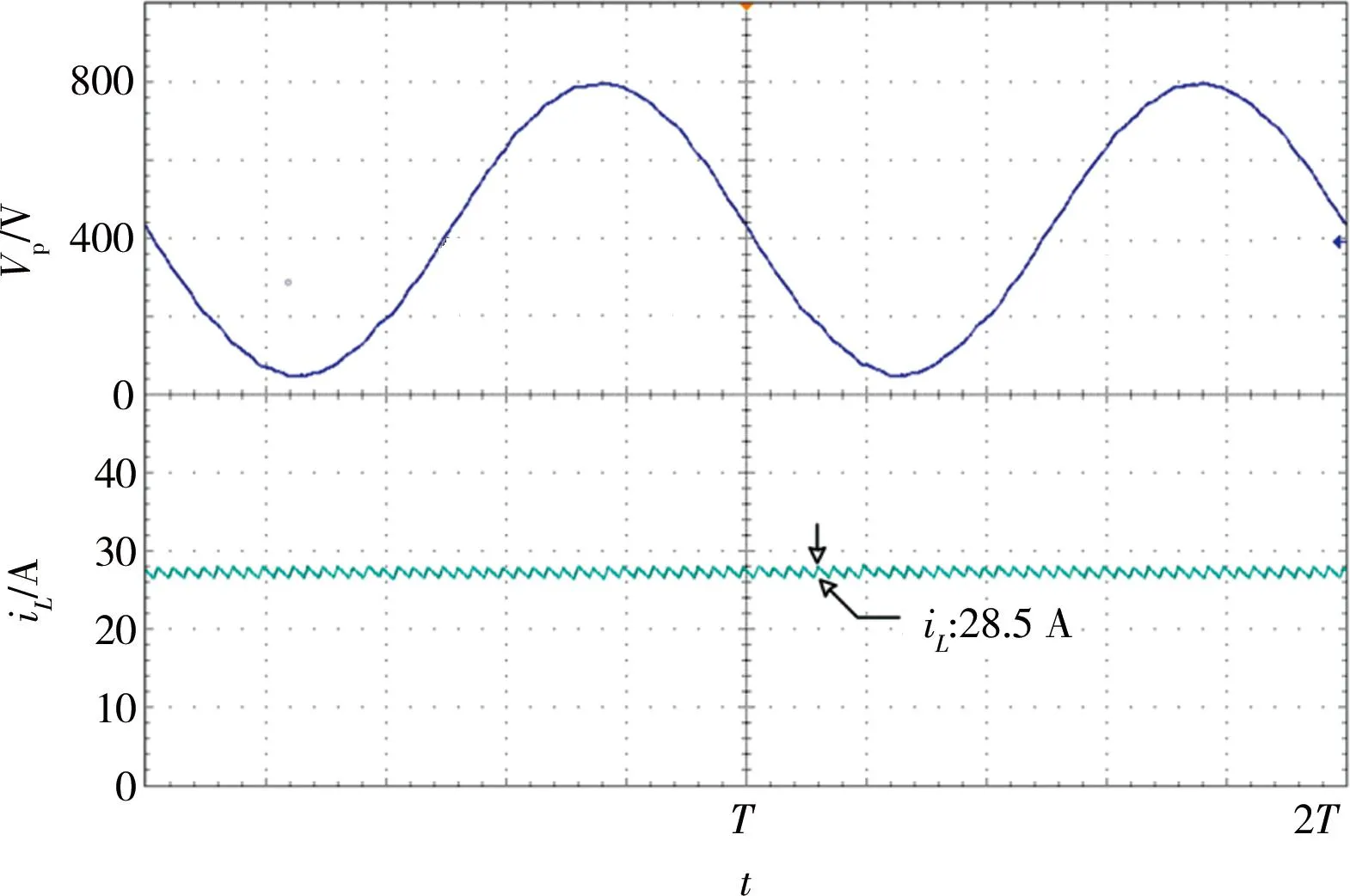
(a)简单升压控制策略

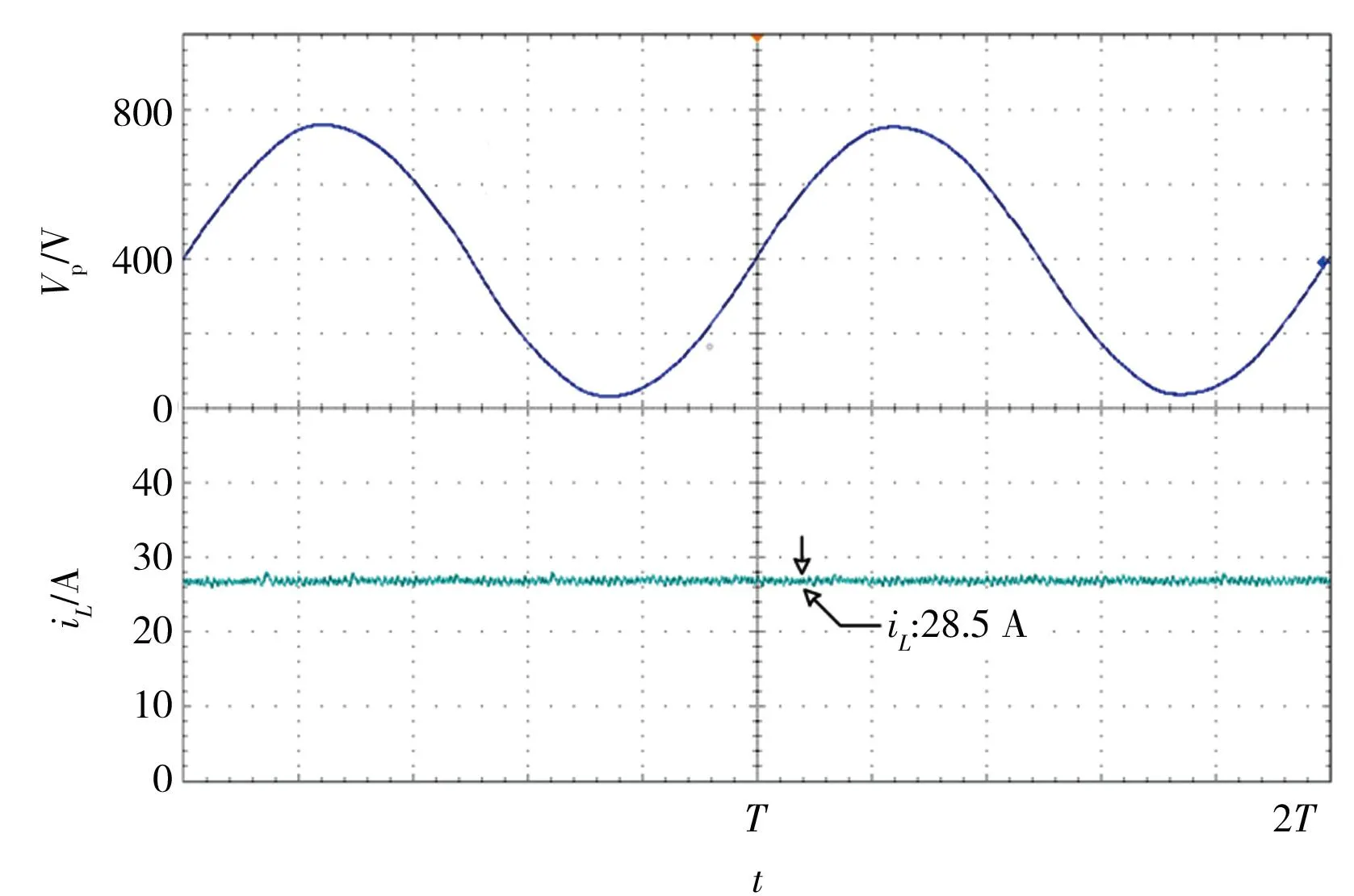
(b)均值信号注入后的控制策略

图13显示了当Vin=500 V时准Z源逆变器直流链电压和电容电压的实验波形。从实验波形可知，注入均值信号后准Z源逆变器的直流链电压和电容电压相较于简单升压控制策略下的均显著降低，和仿真结果保持一致。因此采用注入均值信号分量后的调制策略可使逆变桥功率器件和准Z源网络的两个电容承受更低的电压应力。

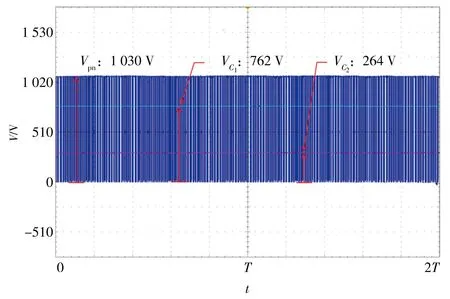
(a)简单升压控制策略

(b)均值信号注入后的控制策略

逆变器桥的开关管电压Vsw和电感电流iL实验波形的局部放大图如图14所示。由图可知，改进的调制策略电感电流脉动明显减少，最大电感电流纹波显著降低。与此同时，从Vsw波形可知，逆变桥开关管承受的电压应力也更小。上述结果表明采用注入均值信号后的调制策略，准Z源逆变器系统有着更低的电压应力和电感电流纹波。

(a)简单升压控制策略

(b)均值信号注入后的控制策略

实验波形

6 结论

本文针对准Z源逆变器采用简单升压控制策略所存在的电压应力大和最大电感电流纹波高的问题，提出一种注入均值分量的控制策略。这种控制策略可以减小准Z源网络最大电感电流纹波，同时有效降低准Z源网络两个电容的电容电压和功率器件的电压应力。通过仿真和实验验证，对注入均值信号控制策略和简单升压控制策略下的性能进行对比，可以得到：

1)采用注入均值信号控制策略下的电压应力相较于采用简单升压控制策略下的显著减小，逆变桥功率器件减少约25.67%，电容电压VC1减少约17.02%，电容电压VC2降低了49.92%。

2)提出的调制策略所带来的电感电流纹波性能更优越，在同输入功率、同输出电压情况下电感电流脉动减小，最大电感电流纹波较简单升压控制策略下降低了47.8%。