功能梯度材料三角形截面梁组合扭转理论研究
2024-01-09张文福沙彦文
张文福,沙彦文
(1.南京工程学院建筑工程学院,江苏南京 211167;2.南京工程学院机械工程学院,江苏南京 211167)
目前,在机械工程领域,薄壁结构的应用十分广泛。但是,薄壁结构也有一定的缺点,由于截面较薄,在承受外力时容易发生变形。功能梯度材料(Functionally Gradient Materials,FGM)是由两种或多种材料复合且成分和结构呈连续梯度变化的一种新型复合材料,其概念最早在1984 年由日本科学家平井敏雄等提出[1]。近年来薄壁构件逐渐受到重视,在材料制备中可采用功能梯度材料,通过将陶瓷、塑料、金属等巧妙组合,充分发挥各类材料的优势。
在薄壁结构中,相比于开口截面,闭口截面具有更好的抗扭和抗剪性能,但目前针对闭口截面薄壁构件的研究多集中在箱型截面,对其他类型的闭口截面如三角形截面的研究较少,且多集中在三角形桁架梁或桁架拱结构。在静力研究方面:文颖等人[2]提出了混合截面的约束扭转有限元模型;何海玉等人[3]提出了倒三角形截面的钢圆弧拱在全跨均布载荷作用下的极限承载力公式;杨则英等人[4]提出了计算平面曲线梁温度变形的简单算法。在动力研究方面:Dikaros等人[5]提出了任意单连接或多连接闭口截面梁的非均匀翘曲动力学分析的一般公式;Wang 等人[6]确定了弯曲箱梁的7个基本位移,在曲线坐标系下建立了一个三节点曲梁有限元,用于曲箱梁的振动特性和动力响应分析;Carrera 等人[7]采用改进的梁理论,对叠层复合材料箱形结构的自由振动进行了讨论,采用Carrera统一公式建立了高阶模型;Jiang等人[8]建立了薄壁箱梁的改进单元刚度和质量矩阵。
近年来,功能梯度材料的国内外研究成果逐渐增多。在静力研究方面:Avhad等人[9]采用Navier解法得到了功能梯度组合梁在高度上弯曲的应力和挠度;Sayyad等人[10]对功能梯度多孔圆形梁的静态变形和振动频率进行了分析,获得了静态和振动问题的Navier型封闭解;Sayyad等人[11]则提出了一种多项式型五阶弯曲梁理论。在动力研究方面:江希等人[12]利用Pei 研究的针对功能梯度材料梁的新型高阶梁理论,将其由静力学领域拓展到梁的模态分析,并通过构造新型高阶单元,采用有限元方法研究功能梯度梁的前三阶自由振动;Sayyad等人[13]提出了一种新的针对功能梯度曲梁自由振动分析的高阶剪切法向变形理论;Sharma等人[14]研究了轴向锥形功能梯度(AFG)梁的固有频率。
然而,作为一种新型的复合材料,功能梯度材料现有的研究多集中在材料性质、寿命及制造方面,由其制造的薄壁构件的力学性能还需进一步探讨。本文基于板-梁理论,按材料性质沿板件厚度梯度变化情形,对三角形截面悬臂梁的组合扭转进行研究;利用有限元软件ANSYS 建立了相应模型,并对研究结果进行了验证。
1 FGM 三角形截面梁组合扭转理论
1.1 基本假设
1.1.1 刚周边假设
板件的横截面在其面内的刚度是无限大的,因此在构件发生扭转时,横截面在其轴向投影的形状保持不变。
1.1.2 变形假设
将板件的变形分解为平面内变形和平面外变形两部分,这样可以简化分析。
1.1.3 板-梁假设
板件的平面内、平面外纵向位移和应变能分别由Timoshenko梁理论和Kirchhoff板理论确定。
1.2 计算简图
如图1所示等腰三角形中:bf为上翼缘宽度,tf为上翼缘厚度,bw为腹板宽度,tw为腹板厚度,C 为截面的形心,S 为截面的剪心,梁长为L。o-xyz 为截面整体坐标系,原点位于形心,x 轴与翼缘平行,y 轴为截面的对称轴。o-nsz 为各块板的局部坐标系,均符合右手螺旋法则。hs1为上翼缘自身形心到剪心的距离,hs2为腹板底部到剪心的距离,ef1为上翼缘自身形心到整个截面形心的距离,ew为腹板形心到整个截面形心的距离,β为等腰三角形对称轴与腹板的夹角。

图1 三角形截面尺寸图
如图2 所示,为三角形截面扭转变形前后对比图。
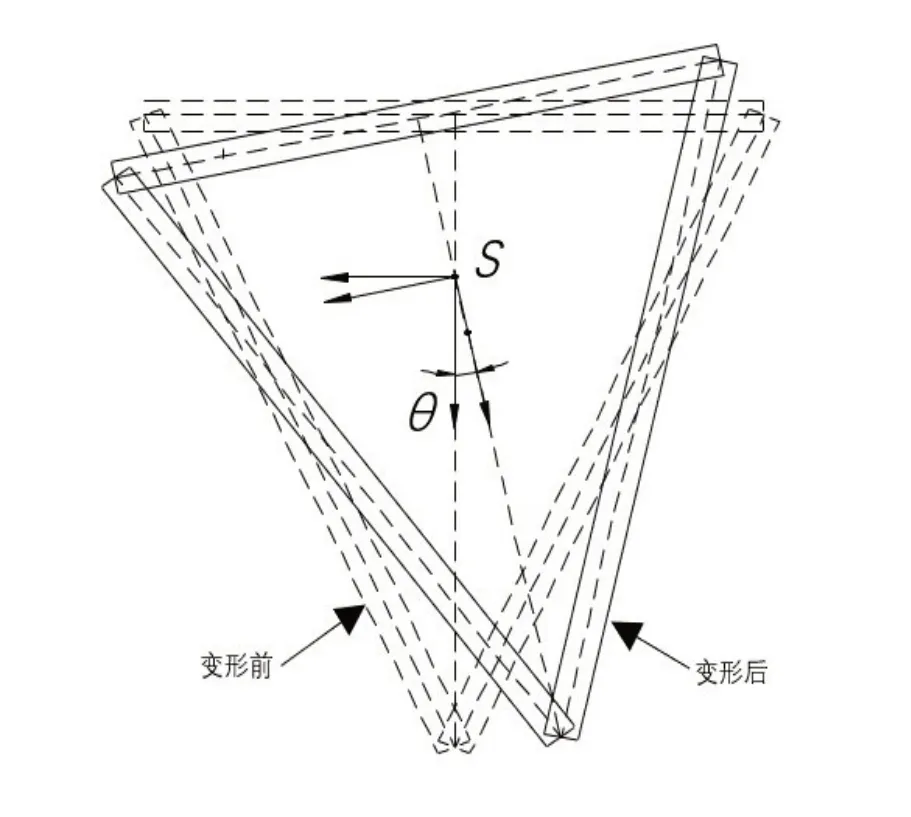
图2 三角形截面扭转变形图
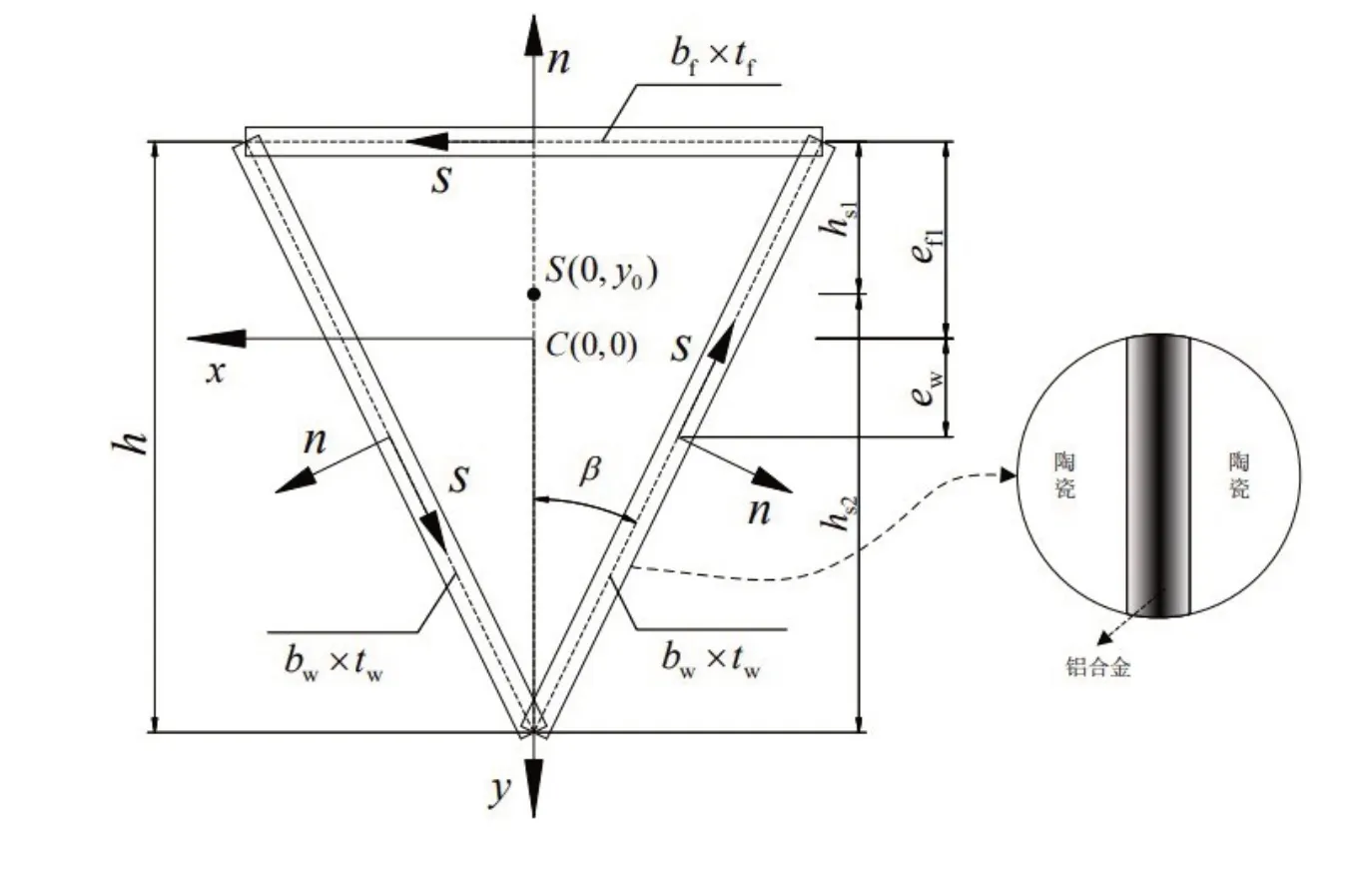
图3 材料性质沿板件厚度方向变化示意图
1.3 截面的形心与剪心
根据文献[15],得到公式(1)和公式(2)。(1)截面的形心
其中,Aw和Af为三角形截面腹板和上翼缘的面积。
(2)截面的剪心
其中,Iy,w和Iy,f为三角形截面腹板和翼缘的惯性矩。
1.4 材料性质沿厚度变化的组合扭转理论
1.4.1 左腹板截面任意点位移
根据变形分解原理,可将左腹板任一点位移写为:
其中:等号后第1 项为左腹板平面内的横向位移;第2项为左腹板平面外的横向位移。
1.4.2 左腹板平面内弯曲应变能
应变能公式为:
其中,E(n)和G(n)分别为功能梯度材料的弹性模量和剪切模量,两者关系为:
式中μ为泊松比,且弹性模量的变化模式为:
式中:pw=1,2,3…,为腹板功能梯度材料的梯度指数;Emw为腹板厚度方向中部的弹性模量;Eow为腹板厚度方向外边缘的弹性模量;mw=EowEmw=GowGmw为腹板外边缘与中部的模量比。
由平面内位移的表达式(3)可得左腹板内某一点的位移为:
沿着左腹板n 轴的位移
沿着左腹板s轴的位移
纵向位移根据Timoshenko梁理论可以表示为
其中:ψw1是闭口截面构件中因剪切变形导致的截面转角,后面需要用截面扭转角θ 加以确定;b1是因左腹板的形心不在截面主轴上而引起的纵向位移。
线性应变为:
根据应变能公式(4)及线性应变公式(5)(6)(7),则左腹板平面内应变能为:
式中χ3是考虑功能梯度材料模量变化影响的修正系数,其表达式为:
1.4.3 左腹板平面外弯曲应变能
同上方法,则左腹板平面外应变能为:
式中χ4是考虑功能梯度材料模量变化影响的修正系数,其表达式为:
综上,左腹板扭转应变能为:
由对称性,左右腹板的扭转应变能相同,即Uw1=Uw2。同上方法也可得到上翼缘的应变能为:
式中χ1、χ2是考虑功能梯度材料模量变化影响的修正系数,其表达式为:
1.4.4 截面扭转角与横截面转角的关系
在上述三角形截面的应变能计算中,根据文献[15],截面扭转角θ 与截面转角ψf、ψw1、ψw2的关系如下:
1.4.5 截面总应变能及总势能
三角形截面总应变能为:
当翼缘和腹板的材料性质变化一致,即Emf=Emw=Em时,应变能表达式简化为:
式中:
为截面的翘曲惯性矩;
为截面的自由扭转常数;
为考虑功能梯度材料模量变化影响的修正系数。
若在自由端施加集中扭矩Mt,则外力势能为:
截面的总势能为:
1.4.6 能量微分方程模型
依据能量变分原理,由δΠ=0可得:
采用分部积分法最终得到:
可得如下微分方程:
1.4.7 悬臂梁扭转角的精确解析解
对式(13)微分方程模型求解,并结合边界条件可得扭转角表达式为:
所以,最大扭转角即自由端的扭转角为:
其中,K 为薄壁构件的扭转刚度参数(无量纲),是反映自由扭转扭矩和翘曲扭转在总扭矩中所占比例的重要系数。
2 FGM 三角形截面梁组合扭转有限元验证
以图4 所示的材料性质沿板件厚度变化三角形截面悬臂梁扭转角为例,进行有限元验证。
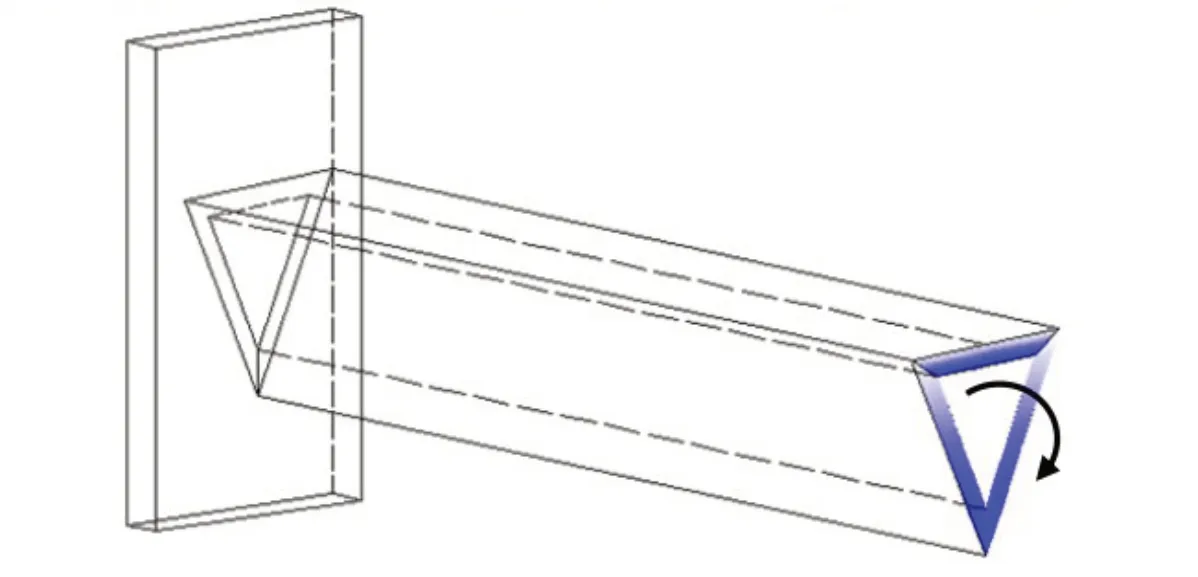
图4 悬臂梁在自由端作用集中扭矩
2.1 有限元模型的建立
2.1.1 基本假定
构件的变形是微小的,即小变形;材料始终处于弹性阶段;构件发生扭转时可以翘曲,但横截面轴向投影的形状不发生变化。
2.1.2 边界条件
因为本文研究的是悬臂梁的组合扭转,所以约束条件为:在固定端约束所有自由度;在自由端施加集中扭矩;在每个截面处使用CERIG 命令建立刚性域,保证截面上所有节点的扭转位移一致。
2.1.3 单元选择
在ANSYS中模拟功能梯度材料可以通过分层来解决,赋予每层不同的材料性质,包括弹性模量E 和剪切模量G。ANSYS 中的SHELL99 可以模拟平板和曲壳一类结构,也适用于模拟薄壁结构,一个单元最多可以分成250层,从而能够较为精确地模拟功能梯度材料。
2.1.4 建模及求解过程
在SHELL99 中使用分层技术且每层等厚来模拟功能梯度材料。将第2 个关键选项(KEYOPT)设定为0,然后通过改变实常数(RMODIF)和循环命令(DO-ENDDO),赋予每层单元不同的性质。
在建模时,翼缘和腹板选用同样类型的功能梯度材料:铝合金-陶瓷-铝合金型。铝合金弹性模量为Em=70 GPa,陶瓷弹性模量为Eo=380 GPa,泊松比μ=0.3,梯度指数为2。弹性模量变化形式为二次函数形式:即板件的厚度方向中心为铝合金,而最外部的两侧为陶瓷。
在对每层赋予材料性质后,进行几何建模,施加集中扭矩1 N·m,最后求解。为保证薄壁结构刚周边特性,使用刚域(CERIG)命令,可以保证截面在扭转时形状不变。此外,当悬臂梁在自由端施加扭矩进行组合扭转验证时,为避免自由端发生异常的过度变形,可以使用接触单元(TARGE170和CONTA175)来保证模拟的正确性。
2.2 有限元验证
如图5 所示,根据公式(17)计算了6 组不同尺寸的悬臂梁自由端扭转角,并建立了相应的有限元模型。如表1 所示,为理论值和有限元值的对比数据。

表1 材料性质沿厚度变化的三角形截面悬臂梁扭转角对比数据
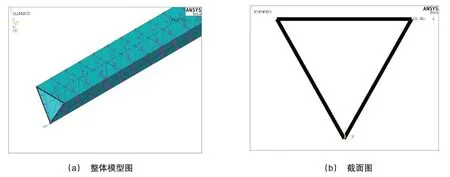
图5 三角形悬臂梁组合扭转有限元模拟图
3 结论
(1)基于板-梁理论,将材料性质按照沿板件厚度变化的情况,推导了三角形截面悬臂梁组合扭转的总势能。建立能量变分模型和能量微分模型,求解得到三角形截面悬臂梁在端部扭矩作用下最大扭转角的表达式。
(2)利用有限元软件ANSYS 对公式进行了验证,结果表明:转角误差在2.77%~4.29%。故公式推导具有一定的合理性,可为工程设计提供参考。
