基于麻雀搜索优化SVR模型的房地产价格研究

兰瑞杰,孟维高,耿进强

(河北地质大学 城市地质与工程学院,河北 石家庄 050031)

近年来房地产价格处于居高不下的状态,房价走势问题成为了社会各界关注的热点话题,而基于房价收入比、房地产产值在国民经济中所占比重等传统指标由于时效性较差,使房地产价格的波动趋势较难预测,因此寻求一种时效性强的房价预测方法显得尤为重要。在大数据时代,互联网的快速发展、互联网用户偏好、媒体信息以及媒体效应对房地产供求市场具有较大影响,网络搜索逐渐成为民众获取信息的主流渠道。因此通过分析影响房地产的相关词条搜索痕迹建立房地产价格预测模型,从而探求房地产价格的变化关系成为一种较新颖的预测方法。

1 文献综述

关于房地产价格波动,由于购房者的视野较大程度上被互联网的媒体信息所主导,研究人员开始研究媒体效应对房地产市场价格的影响。研究人员将媒体效应指标量化为购房者的网络搜索行为[1-3],从数据中发现网络搜索数据对房地产价格市场具有较高的相关性。将网络搜索数据加入房地产价格的回归预测模型中,结果表明网络搜索数据可以提高预测模型精度。这说明了网络搜索数据可以表征用户的信息需求、行为偏好,也说明了网络搜索数据具有较好的数据时效性,可以提高预测结果的准确性。

在对房地产价格进行预测时,研究人员从传统计量模型到机器学习模型进行了大量研究。文献[4]采用灰色系统GM(1,1)模型对包头市房地产每年的价格数据进行房价预测,结果显示模型精度高拟合效果较好,预测结果也表明未来几年包头市房地产价格趋于稳定。传统的灰色模型未考虑各影响因素对房地产价格的影响存在滞后性等缺点,文献[5]通过构建对房地产价格的向量自回归(Vector Auto Regression,VAR)模型,将时间序列滞后特点引入模型,拟合效果较好。但VAR模型的预测能力较差,且灰色系统在进行非线性数据预测时并不能表现出较好的适应性。机器学习例如BP神经网络(Back Propagation Neural Network)与宽容的支持向量机(Support Vector Machine,SVM)能更好地适应线性数据与非线性数据。文献[6]采用了GM(1,1)与BP的组合神经网络模型,结果表明其对有波动性的数据类型有较好的预测精度,并增强了模型的自适应性。文献[7]将VAR-GM(1,1)-SVR这3种模型相结合建立综合预测模型,将计量经济学的VAR模型和灰色预测模型作为模型输入,结果表明该结合式的全新模型具有更好的预测精度。文献[8]以百度指数为数据基础,采用多种传统算法例如线性回归、回归树以及随机森林等对房地产价格指数进行预测。该组合式的模型虽然对预测精度具有较大提升,但是这类机器学习模型在参数选取上有较大的不确定性,模型的泛化能力和稳定性有待提升。文献[9]和文献[10]分别采用蝙蝠算法和粒子群算法对SVR的相关参数进行优化,提高了房价模型的预测精度。

通过梳理文献可知,目前关于房地产价格的传统研究数据主要来源于历年统计年鉴和国家统计局,其数据的时效性较低,影响了预测结果的准确性。运用网络搜索数据建立与房地产价格市场的关系能够减小数据本身对预测结果的影响,具有较好的可靠性和时效性。此外,在房价预测模型方面,研究人员大多采用计量经济模型(二维云预测模型[11]、VAR模型[12]、灰色系统GM和机器学习神经网络[13]以及SVR[14])进行房地产价格预测,但SVR模型在参数选取上仍存在一定的优化空间。因此本文采用时效性较高的网络搜索数据研究房地产价格,根据文献[3、11、15]确定房地产价格网络搜索的关键词库,采用麻雀搜索算法优化的SVR作为房地产价格的预测模型,在选取房地产价格的解释变量数据与算法模型选取方面均具有一定的创新性。

2 算法与模型

2.1 算法流程与模型设计

随着深度学习、人工智能的快速发展,人工智能算法理论也在不断更新。智能算法与神经网络和SVR结合可以优化模型参数,从而提高模型的预测精度和收敛速度。常见的模型优化算法有粒子群算法[16]、遗传算法[17]、鲸鱼算法[18]以及网格算法[19]等。但是这些智能算法在寻优性、全局最优搜索能力和收敛能力方面均有一定的优化空间。基于此,本文采用一种启发于麻雀觅食和反捕食的麻雀搜索算法。该算法比较新颖,具有寻优能力强、收敛速度快以及可寻找全局最优的特点。利用麻雀搜索算法优化调节SVR模型的惩罚参数C和参数g,但该方法在模型应用上具有一定的创新性。

在觅食过程中,麻雀种群分为探索个体和跟随个体。探索者负责寻找食物并确定食物位置和觅食方向,跟随者通过获取探索者共享的信息来进行觅食。麻雀的觅食行为分为探索策略和跟随策略。麻雀种群中的每只麻雀都可以获得其他麻雀所采取的策略和行为。种群中的个体监控种群中其他个体的行为,种群中的攻击者与高摄入量的同伴竞争食物资源以提高捕食率。同时,麻雀也有预警机制,当危险来临时,麻雀会转移到安全区域。高适应度的探索者在种群搜索食物过程中处于高优先级地位,即优先获取食物。探索者为整个麻雀种群提供食物,并且决定跟随者的觅食方向,所以探索者的位置更新范围大于追随者的位置搜索范围。

探索者的觅食位置更新计算式如下所示

(1)

式中,t为种群的迭代次数t∈1,2,…,itermax;j是优化问题的维数j∈1,2,…,d;Q和a是随机产生的随机数且Q服从正态分布;L是1×d的全1矩阵;R2属于0～1表示麻雀种群位置的预警值;ST属于0.5～1.0,表示麻雀种群位置的安全值。当预警值小于安全值时,代表种群处于安全搜索区域,捕食范围较大;当预警值大于或等于安全值时,代表种群接近危险区,整个种群需转移到其他区域觅食。

追随者的位置更新计算式如下所示

(2)

式中,XP表示当前探索者寻找到的最佳位置;Xworst是当前种群觅食的最差位置;A是1×d的矩阵,其值为1或-1;i>n/2表明适应度值较低的第i个跟随者未获得食物,处于紧急状态,此时追随者需要去其他位置觅食。

当危险来临时,种群的危险预警机制更新计算式如下所示

(3)

式中,fi表示当前麻雀适应度值;fg表示全局最佳适应度值;fw表示全局最差适应度值;K是麻雀的移动方向,是控制移动步长的参数。当fi=fg时表示种群发现了危险,需要靠近其他麻雀以减少被捕食风险。当fi>fg时,表示麻雀处于种群边缘,容易被捕食。

2.2 支持向量机

支持向量机(SVM)是一种机器学习的建模方法,其理论基础源自统计学,SVM通过寻找结构风险最小值来提高模型的泛化能力,使经验风险和置信区间最小化,从而达到使用较少的统计样本获得良好的统计规则的目的。

SVR模型是由SVM的分类问题演化而来,分类器模型输出离散值,而回归模型输出连续值。SVM分类模型在引入不敏感参数ε后,得到支持向量的回归模型即SVR。SVR模型具有良好的非线性预测能力,适合小样本数据学习。SVR是预测模型的研究热点,尤其在机器学习、智能算法的推进下,SVR模型得到了不断优化[20]。基本原理如下:

给定样本容量为N的n维训练数据集,当输入变量与输出变量呈非线性关系时,函数形式如下所示

f(x)=ωTφ(x)+a

(4)

式中,a是回归函数的截距项;ω为回归系数;φ(x)是一种非线性的核函数。该函数能够将低维非线性的数据直接映射到一个高维空间,可以将非线性运算转换为线性运算。支持的向量回归实质就是通过寻找回归函数f(x),使全部的训练数据相应函数值和目标偏差都不能超过不敏感参数ε,其目标函数和约束计算式如下所示。

(5)

(6)

(7)

(8)

将式(8)一阶偏导为0求出的结果带入式(6),并引入符合Mercer条件的有效核函数K得到目标函数的对偶问题形式,如下所示

(9)

(10)

得到回归模型的计算式如下所示。

(11)

核函数可以通过非线性变换将原空间内积映射到高维特征空间。在本文模型中,核函数选用RBF核函数即高斯径向核函数

(12)

其中,xi为核函数中心;σ为函数的宽度参数,控制函数的径向作用范围。

2.3 麻雀搜索算法优化的SVR模型

通过麻雀搜索算法对SVR的参数C和g进行优化,建立天津市新房价格指数预测模型。SSA-SVR天津市房价预测模型如下:

步骤1对输入数据和输出数据进行归一化化处理。将房价指数关键词的搜索指数作为模型的输入变量,在筛选影响因素时与房地产价格进行简单的皮尔逊相关系数检验,选取与房地产价格指数相关系数大于0.7的关键词,最终确定房地产价格预测模型的输入变量,有利于提升预测精度。归一化计算式如下所示。

(13)

步骤2设置相关参数。初始化麻雀搜索的种群个数、进化代数、K折交叉,根据种群中探索者和跟随者的比例数量对SVR参数C、g的范围进行设置。

步骤3生成新的个体。按照式(2)～式(4)对探索者、跟随者以及预警机制下麻雀进行位置更新,不断迭代生成新的解,并记录当前探索者位置最优解以及全局最优解。

步骤4评估适应度函数,得到适应度最佳的个体。SSA应采取适当措施以确保最佳的参数设置,从而提高模型的预测精度。在SSA算法优化模型参数时,采用K折交叉验证(K-CV)方法,K折交叉验证可有效解决模型泛化能力差过度拟合的情况,选取预测模型的均方误差作为适应度函数。K折交叉验证利用了无重复采样的优势:每个个体在每次迭代中只有一次机会被包含在训练或测试集中。结合本文样本容量大小,取k= 5。模型评价指标均方误差(Mean Square Error,MSE)如式(14)所示。

(14)

步骤5停止循环标准。有两个停止标准,一个是迭代次数达到设定标准,另一个是模型误差达到预期水平。当迭代满足停止条件时输出预测结果,否则重复步骤3和步骤4,直到迭代次数达到预设值。通过循环迭代得到最佳的适应度函数值,获取最佳的模型参数。再将麻雀搜索算法得到的最佳模型参数C和g运用到SVR模型中,将数据分为训练集和测试集进而得到房价指数预测模型。

麻雀搜索算法优化的SVR房价预测模型算法流程如图1所示。

图1 麻雀搜索算法优化SVR流程Figure 1. Sparrow search algorithm optimization SVR flow

3 网络搜索数据选取

3.1 数据来源

百度指数是以百度搜索为基础的用户行为为基础的数据分析平台,是目前的主要数据分析平台之一。以通过分析影响房地产的相关词条搜索痕迹为解释变量建立房地产价格预测模型,数据来源为百度指数网上影响房地产价格的关键词。采用Python工具选取与关键词相关指标数据2011年1月～2021年3月近20万条日数据,并汇总为月数据作为解释变量。

房地产价格选取天津市新房价格指数作为被解释变量,数据来源中国指数研究院数据库,范围为2011年1月～2021年3月的月数据,样本来源天津市所有包括商业用房、写字楼以及居民住宅在售商品新房项目。在进行训练集划分时,为了避免模型出现过拟合现象,对2011年1月～2021年3月共计123个月的样本数据进行随机取样预处理,随机选取其中36个月作为测试样本,其余样本作为模型的训练样本。

3.2 搜索数据筛选

房地产价格相关网络搜索数据可以反映购房者潜在的相关需求,但并不是所有网络搜索数据都与房价具有显著关系。通过文献和百度推荐得到的与天津市房地产有关搜索关键词需要进行一定的数据分析处理,才可作为天津房地产价格的被解释变量。初始关键词要尽可能覆盖所有与房地产价格有关的关键词,对关键词与天津房价指数进行相关性分析,剔除无效关键词,得到与房价指数相关的关键词,可以提高模型的预测能力。本文对网络搜索数据确定和选取步骤如下:

步骤1首先确定网络搜索数据的初始关键词库。本文采取百度相关推荐与文献查阅方式,分别从供给、需求、替代、政策、金融以及财政等方面选取与天津市房价市场有关的55个初始关键词,如表1所示。

表1 初始关键词库

步骤2采用R语言作为数据分析工具,对所有解释变量与被解释变量进行相关性分析,选取相关性大于0.7的解释变量,剔除不显著相关的解释变量,提高预测模型的准确度。剔除后解释变量与被解释变量的相关系数如图2所示。

图2 相关系数热力矩阵Figure 2. Correlation coefficient thermal matrix

y为被解释变量天津房地产价格指数,x1～x9分别为:安居客、存款基准利率、存款利率、房地产营业税、房天下、链家、人才引进、物价税、天津房价指数滞后观测量。

4 实证分析

4.1 基于SSA-SVR的天津房价指数预测

因为单一误差指标并不能完全体现预测模型的可靠性,为验证和比较SSA-SVR模型与其他基准模型的预测性能,本文采用相关系数r、均方根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)和平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)等指标对预测模型进行评价。评价指标的计算式如下所示。

(15)

(16)

(17)

(18)

(19)

图3展示了在麻雀搜索算法过程中所有麻雀适应度的平均值变化以及最佳适应度变化曲线,适应度曲线可以看出算法的收敛速度寻优能力较好。且经过麻雀搜索算法寻优得到最佳参数C为348.59,g为0.24,即麻雀搜索算法训练所得的SVR最佳参数。

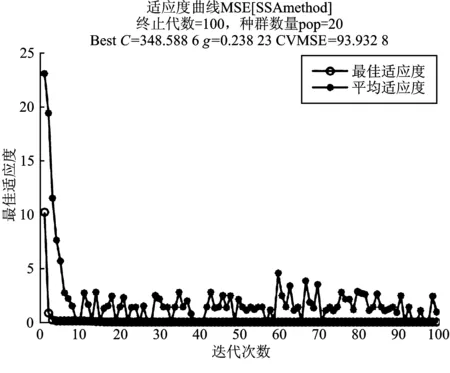
图3 麻雀搜索算法适应度迭代Figure 3. Fitness iteration graph of SSA

为进一步研究本文模型的预测性能,将天津市新房价格指数作为被预测变量,随机抽取36个样本作为测试样本,其余样本作为测试样本。模型所得测试样本的预测结果如表2,测试集训练集与测试集误差对比如图4和图5所示。

表2 SSA-SVR模型测试样本预测结果

图4 训练样本真实值与预测值对比Figure 4. Comparison of actual and predicted values of training samples

图5 测试样本真实值与预测值对比Figure 5. Comparison between the actual value and the predicted value of the test sample

由表2可知,真实值与预测值误差在5以内的样本有21个,误差在3以内的样本有15个,误差在1以内的样本有8个,误差整体偏小,表明模型具有较好的预测性能。由图4可以看出,两个样本的真实值和预测值几乎都在同一个点上,说明该预测模型预测精确度较好。同时对比训练样本和测试样本两个误差分析,并未出现训练误差远小于测试样本误差情况,说明模型的泛化能力较好,未出现过拟合现象。

4.2 预测模型评价

图5反映了SSA-SVR模型在基于网络搜索数据为输入的房价预测数据样本区间具有较好的拟合效果,预测与实际值的误差较小,说明麻雀搜索算法优化SVR混合模型具有较好的预测性能。由图5可以看出,模型在训练样本和测试样本均具有较好的拟合效果,平均绝对百分比误差(MAPE)在训练样本为0.25%,在测试样本为0.33%,进一步说明该模型具有较强的泛化能力。

为进一步研究麻雀搜索算法是否优化了模型的预测精度,将SSA-SVR与PSO-SVR、GA-SVR、WOA-SVR、GS-SVR和基准SVR进行模型对比。评价标准为相关系数r、均方根误差(RMSE)、平均绝对误差(MAE)、均方误差(MSE)以及平均绝对误差比(MAPE)。对比结果如表3所示。

表3 模型误差分析

通过模型对比可以看出,利用智能算法对参数优化对SVR模型的预测精度具有较大提升。通过不同智能算法之间的对比可以看出,麻雀搜索算法具有更好的全局寻优能力,麻雀搜索优化算法可以提高模型的预测准确度,提升模型的预测能力。

5 结束语

机器学习模型在进行房价预测时,若采用传统经济指标作为房价的影响因素数据,数据滞后性问题会使预测精度降低。此外,模型参数的设定对预测模型的精度同样具有较大影响。因此本文采用一种新型的智能算法麻雀搜索算法SSA优化SVR模型相关参数,并选取近20万条网络搜索数据,将筛选得到的数据作为解释变量进行验证。对比基准模型与不同智能算法优化模型的预测性能指标例如均方误差和平均百分比误差的结果表明麻雀搜索算法优化的SVR模型在房价预测精度与泛化能力上均具有较好的提升。