基于近场声全息的故障诊断技术研究综述
2024-01-09张宏宇吴晓阳
张宏宇, 吴晓阳, 栾 鑫
(武警海警学院 机电管理系, 浙江 宁波 315801)
机械设备在运行过程中往往会产生一定的振动噪声,这些振动或噪声信号能够反映出设备运行的某些状态信息,如轴承磨损、螺栓松动等[1-2],但对于振动探头不便布置等情况,传统振动检测方法难以监测,且非专业人员也很难从振动数据中分析出设备产生故障的位置。在工厂或船舶机舱等封闭环境中,设备产生的噪声会对人员的身心健康造成损害,通常需要准确找到噪声源位置,并采取对应的减振降噪的方法[3]。因此基于声学信号对设备进行非接触式状态监测具有广泛的应用价值。
早期的声学检测技术是基于声学频谱分析,利用单个或两个传声器来记录噪声频谱成分的变化,实现对设备的实时监测[4]。这种监测只能在时频域中分析噪声辐射,并不能给出声源的位置信息,而且受环境噪声干扰较大,监测效果并不理想。随着声学传感器性能的提升,以及数字信号分析技术和阵列信号处理技术的应用,基于声传感器阵列的监测技术发展迅速,特别是以近场声全息(near-field acoustic holography,NAH)理论为基础的声成像技术,通过采集声场空间中不同位置点的声学参数信息,重建声场状态,分析得到声源的位置信息并将其转化为直观的图像[5],方便人员掌握噪声源位置,进行故障检测。
几十年来,国内外众多学者围绕近场声全息技术重建声场进行了大量研究,广泛采用多种数据处理方法改进重建算法,并利用近场声全息计算得到的声学参数特征作为故障诊断基础[6-7],通过不同的诊断策略进行故障检测,不断提高近场声全息技术的实际应用效果。现从近场声全息技术的基本理论出发,系统地介绍几种近场声全息的声场重建算法,分析不同算法的特点,并对近场声全息算法的发展趋势进行展望。
1 近场声全息理论
声全息技术起源于19世纪80年代,学者们借鉴光全息技术,基于声波的波动性提出声全息概念,希望通过一定手段的测量获得整个声场的信息。但这种声全息方法受全息理论限制,重建声场的分辨率不超过声源的辐射波长,也就无法得到小于波长的声源细节,而光波的波长很小,这对光学全息的影响并不大,但在声学中有很多声源体的尺寸比声波波长小得多,严重限制了基于声全息技术的振动结构特征分析。
之后人们发现,声场的传播中存在着传播波和倏逝波两种类型的波,传播波辐射良好,能将能量传递到远场,而倏逝波的辐射很差,呈指数衰减,永远不会离开声源的近场范围。1985年,Maynard等[8]提出通过在声源近场的共形面上测量声压,采集声源的倏逝波成分,并基于声场传播规律,利用空间卷积和傅里叶变换方法计算声源表面声压、声矢量强度等参数的空间分布,从而获得重建表面的亚波长分辨率,明确提出了近场声全息的基本理论,为近场声全息的研究奠定了基础。
该理论的基本原理是基于声辐射在声场中传播遵循波动方程的规律,将声全息问题看作是利用空间表面参数求解任意位置参数的过程。如图1所示,在声源体D的声场环境中,封闭曲面S所包裹空间为自由声场环境,封闭曲面S由半径无穷大的半球面S1和平面S2组成,r和rS为位置矢量,表示空间位置,曲面S内任意位置点的复声压满足Helmholtz方程,即
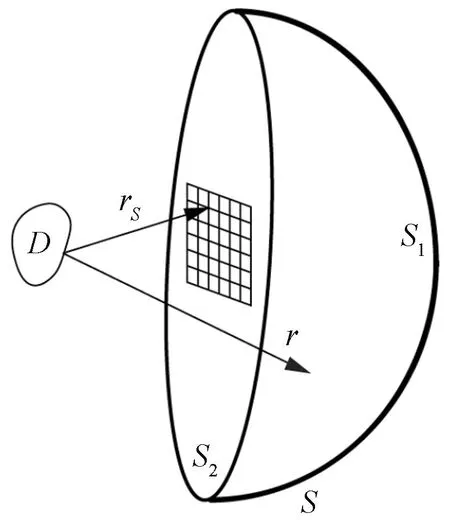
图1 近场声全息原理图
∇2p(r;ω)-k2p(r;ω)=0
(1)
式中:p(r)为曲面S内任意位置r处的复声压;ω为声波频率;k=ω/c0为声波的波数,c0为介质中的声速。
采用格林函数法求解方程(1),可得
(2)
式中:p(rS)为曲面S上的复声压值,通常由传感器阵列测量得到;G(r,rS)为曲面上的格林函数,不同边界条件下的格林函数不同,通常有Dirichlet边界条件、Neumann边界条件和混合边界条件。其中Dirichlet边界条件中的测量面参数为声压值,Neumann边界条件中的测量面参数为法向上声压的导数值,混合边界条件则是两者皆有。
在Dirichlet边界条件下,G(r,rS)一般表示为G(r,rS)=rd(1-ikr)eikr/2πr3,其中r=|r-rS|,rd为测量面与全息面的距离。通过传感器测量得到边界面上的声压信息后,利用式(2)即可求解得到空间内任意位置点的声压,实现声场的重建。
该理论提出了通过传感器阵列采集声源近场数据来构建声场全息图像的模式,并给出了声场重建的基本理论和求解算法,由此可以为运行中的机械设备建立声场全息图,借鉴设备振动监测的原理,分析机械设备不同故障下的声像图特点,进而通过声学监测实现对设备故障的诊断。
采用近场声全息方法进行设备故障诊断时,准确获得设备运行状态下的声像图是至关重要的。但在实际应用中近场声全息方法还存在许多限制。例如,只适用于球状、柱状等规则形状的声源,要求测量阵面与声源共形;受环境影响较大,只能适用于自由声场环境,声场的重建效果很容易受到反射噪声干扰;传感器阵列在采集声场信息时,受采样定理限制,需要采集大量数据确保准确采样,同时为了获取较高分辨率声场信息需要大量的传感器,并且要求传感器间隔也要适当小,导致测量阵列的成本增高,算法的数据处理量也会增加,严重影响近场声全息的实时重建速度,这些问题都与声场重建算法有密切关系。
为此,众多学者基于近场声全息的基本理论,为得到识别精度高、计算速度快和应用环境广的声全息算法,围绕声场重建算法进行了广泛研究,主要形成了两类方法:一是利用卷积定理求解重建方程的解析解,通过傅里叶变换将其转换到频域,在频域中转换为简单的乘除运算,再通过傅里叶逆变换得到重建面声压,也称为傅里叶变换法;二是将方程离散后,通过计算机算法运算得到其数值解,根据求解思路不同有多种算法,如边界元法、等效源法。
目前主流的近场声全息算法有基于快速傅里叶变换算法(fast fourier transformation, FFT)、基于边界元方法(boundary element method,BEM)、基于等效源法(equivalent source method,ESM)、基于Helmholz方程最小二乘法(helmholz equation least squares method,HELS)等。
2 近场声全息算法
2.1 快速傅里叶变换算法
基于FFT算法是最早被提出的一种近场声全息算法。Maynard等[8]在提出近场声全息的基本理论时,将声全息重建过程看作是声场中传感器测量的边界值与格林函数的卷积,采用傅里叶变换的方法来求解声场重建方程(2),并基于该算法对矩形板表面声强进行了重建,验证了近场声全息方法具有较高的分辨率,同时分析了在声场测量中测量区域的有限性。如图1中曲面S2上的测量阵列,由于无法完整测量整个曲面上的复声压值,在重建声场参数时存在不可避免的卷积误差。
多年来,在实际应用过程中发现,测量阵列尺寸至少是声场重建区域的两倍时,也就是在每个方向上额外测量50%的声场数据,可以保证全息重建的准确性,因此近场声全息技术多用于声源体的局部声场重建。近些年来一些学者采用数据插值的方法来扩展测量阵列数据,形成了Patch近场声全息方法。Harris等[9]基于声压梯度的埃尔米特插值方法得到扩展阵面的数据,提高了阵面测量数据的丰富度,一定程度上降低了算法的重建误差;Gu和Zhang[10]通过对测量数据补零扩大数据阵列,并利用重建算法迭代求解扩展阵列面的声场参数,在有限传感器阵列下有效提高了算法的分辨率;He等[11]基于测量声压矩阵和传递格林函数得到等效源密度,并通过埃尔米特插值方法得到扩展数据,一定程度上降低了算法的重建误差;扈宇等[12]提出稀疏贝叶斯方法来对测量阵面的数据进行插值和外推,增加了测量孔径以及阵列数据密度,全息成像的分辨率和准确性有了较好的提高。
为了充分发挥测量传感器的作用,采用少量传感器获得较好的测量效果,通过一定方法来实现实际采集数据的插值和扩展,从而达到大尺寸、高密度传感器阵列测量声场的效果。目前数据的插值和外推方法主要有两类:一是直接对需要补充的位置点补零,并通过近场声全息算法迭代获得扩展的测量面数据阵列;二是采用一定的数学插值方法来扩展测量阵列数据,并通过全息算法或声场辐射规律来修正阵列数据。这些方法一定程度扩大了近场声全息的测量孔径,降低了声场的重建误差,但扩展数据的准确性并不够,还需要重复迭代修正,导致计算运算量较大,影响声场的实时重建,应当寻找合适的数据插值外推方法。
为了解决不同形状声源的声场重建问题,Williams和Dardy[13]基于共形面采集数据方法提出柱状声源重建的广义近场声全息方法,通过二维傅里叶变换方法得到圆柱声源面上的声压分布规律,并分析了声源分辨率和k-space的滤波问题,提出了一种声源重建的算法,对有限的圆柱形声源进行声场重建实验,展现了共形采集数据处理的重建优势。之后一些学者借鉴应用到不同形状声源的声场重建中。Cheng等[14]提出了一种基于变半径圆柱波函数和非保形面测量的锥形声源体的方法,将近场声全息方法拓展到了圆锥曲面,显著提高了大型锥体声场重构的鲁棒性和精度。但这些方法本质上都是基于FFT算法对不同声源形状的应用,但存在明显的局限性,无法适用于其他复杂形状的声源体。
此外,利用计算机求解重建方程时,离散形式重建方程中的格林函数有放大作用,会将测量的环境噪声和误差直接放大,导致重建声场的信噪比大为下降,从而影响了成像的分辨率和重建结果的不适定。因此,在运用FFT方法的过程中,为了提高算法的有效性和抗干扰能力,需要加入滤波函数对测量数据进行滤波处理。Fleische和Axelrad[15]首先提出运用维纳滤波来解决这一问题,该方法有效改进了声场重建的稳定性,但对于高波数域的误差并没有很好地解决。近年来部分学者从声全息传播函数的构建进行研究,设计合理的滤波方法。Ramapriya等[16]基于相关函数与声波相位空间分布的关系,利用量子力学中维格纳函数指示波场信息的特点,通过维格纳变换方法作为相关函数建立的依据,较好地滤除了高波数域的干扰;Zhang等[17]用稀疏正则化方法,分解重建面上的粒子速度来进行声场的重建,有效抑制了高波数域分量。这些方法在一定程度上改进了算法的抗干扰性,使FFT算法能够运用于实际设备的检测。
多年来,该方法在设备故障检测和噪声定位中进行了广泛应用,为设备故障的检测提供了经验。Hou等[18]提出了一种基于近场声全息技术的齿轮箱故障诊断方法,并通过分析声场分布信息进行故障诊断,基于声场纹理特征来对比识别不同故障下的齿轮箱,但存在模式特征不够明显、诊断时间较长的问题;Guo等[19]针对旋转机械的噪声定位问题,利用包络调制技术提取的包络信息重构声场,提出了一种将包络声场信息与近场声全息方法相结合的旋转机械识别噪声源的方法,在保证定位精度的同时加快了定位速度,距离故障诊断还有一定的差距;Wang等[20]针对近场声全息方法测量采样率低的问题,基于深度学习中截断填充方法提出一种圆柱坐标系下的改进算法,在较低的采样频率下保证了足够的声场重建精度,但该方法还是限制在柱状声源的重建,具有一定局限性。这些方法通过结合不同采样技术和算法来提高设备故障噪声的定位准确度,为建立故障检测分析模型奠定基础。
分析可知,该方法算法程序简单、工程应用简洁,但在求解过程中,为得到方程的解析解,一般基于直角坐标系、柱坐标系或球坐标系下进行分离变量求解,导致该方法只适用于平面、柱面和球面等规则声源的全息测量。而且为了便于方程求解,需要在声源共形面上测量声压数据,对于不规则的声源面,一般需要计算声源面附近的规则面来拟合实际声源面,因此并不能准确地重建声场声压分布情况。通过计算假设的规则源面来替代实际声源面的声压,这在一定程度上限制了其定位的精度和提供的信息量,也限制了其应用的范围。
2.2 边界元算法
为将近场声全息应用于任意形状声源的声场重建,研究人员联想到有限元计算方法,结合声场辐射的传播规律,提出了边界元算法。Veronesi和Maynard[21]结合常数边界法,建立了声源体表面与声场点之间的传递函数,将声场重建转化为矩阵方程的求解过程,建立了边界元算法的基本思路,但该方法的重建精度低,无法实际应用。之后Bai[22]采用形函数方法进一步改进完善了边界元算法,并通过奇异值截断来解决矩阵方程的不适定问题,使得边界元算法有较好的声场重建效果。
边界元算法是基于Helmhotlz积分方程,建立声场点声压与声源结构表面声压之间的关系,将声源表面网格化处理,积分方程离散化为如下声场传递方程:
(3)
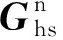
经过矩阵变换运算得到
Ph=KhsPs
(4)
式中:Khs为测量面和声源面之间的传感矩阵。通过对方程(4)进行逆运算得到声源表面的声压分布,从而实现声场重建。
分析边界元算法的求解过程可知,边界元划分的选择对于声场重建的精度有直接的影响。类似有限元的分析方法,边界元算法首先要对声源表面进行网格划分,划分的形状、大小、形函数的选择都对算法重建声场的效果以及算法运行的速度有很大影响,常见的有采用常数、一次和二次边界元。近几年来等几何边界元法发展迅速。Simpson等[23]通过T样条离散化划分边界元,得到较好的重建精度。总体而言,边界元的划分与算法运算量之间存在着需要平衡的考虑,合理地选择边界元划分方法有利于边界元算法的声场重建;Lu和Chen[24]将细分网格中的控制点设置为设计变量,选择观测点处声压最小化作为设计目标,提出了一种将等几何细分面与边界元法相结合的声学形状优化方法,消除了声场重建中产生的锯齿几何形状,并且不需要烦琐的网格划分过程和体积参数化,有效地改进了边界元算法过程;Bruno和Antonella[25]考虑等几何边界元法来进行求解,采用参数化组合的张量积B样条(B-spline)基函数来进行拟合,并通过阈值选择对正则积分和奇异积分的情况进行分别处理,在少量均匀分布的正交节点下实现了足够的数值解精度。
边界元方法是基于Helmholtz积分方程的进行的离散化求解,但在声源的特征频率处,该算法得到的解并不唯一,并且会出现超奇异积分问题,导致计算过程很复杂,虽然有组合亥姆霍兹积分方程公式(combined helmholtz integral equation formulation,CHIEF)法和Burton-Miller法能解决该算法的非唯一性问题,但在计算中往往会增加选取的边界元内点,导致计算量的增加。Valdivia和Williams[26]指出了在边界元离散化中使用高阶形状函数对求解方程不利的问题,提出采用新的隐式求解方法来求解重建算法中的积分方程,相比传统算法计算量相对减少。同时,该方法在求解过程中,由于传递函数Khs常常是病态的,为了确保求解结果的稳定性和准确性,需要通过合适的正则化处理来进行求解。正则化处理的思路就是通过用一个适定方程的解来近似得到原方程的解。Valdivia[27]针对时域边界元法中合成矩阵的结构和稀疏性,通过Krylov子空间迭代的方法来求解声场重建矩阵方程的数值解,进行正则化处理,有效缓解了对任意形状声源声场求解过程中的不适定情况;Zhang和Xiao[28]基于边界元法研究了阵列数据外推插值问题,并通过修正的吉洪诺夫正则化来解决扩展数据求解的不定性问题,得到了较好的重建效果。目前这些正则化方法多是基于L2范数的求解,该方法需要选择合适的正则化参数,而且得到的解也趋向于平滑模糊,符合最小能量分布的状态,并不符合大部分声源稀疏的情况,是针对特定情况下的正则化方法改进,能够解决特定情况的不适定求解问题,对于合适的正则化方法选择还有待于研究。
边界元算法可以用于不同形状声源的声场重建,以及其有限元分析问题的思路,很适合工程实践中应用。例如,Williams等[29]采用55通道传感器阵列对贝奇1900D(UE1)飞机的高空飞行中的机舱进行了声场重建,揭示了从发动机到内部空间的结构机舱声音传播路径,求解过程中的正则化处理较为经验化,得到的声场全息图存在一定的误差;Wu等[30]在嘈杂的环境中,基于边界元方法引入双层声压测量来重建声源的自由场,并将求解方程转化为舒尔补方程与Tikhonov正则化方法结合使用来获得较好的重建效果,通过对钢制立方箱体进行了实验,验证了嘈杂环境下进行声场重建的准确性和有效性;Luo等[31]基于边界元法提出一种在噪声混合场中恢复任意形状声源辐射的自由场方法,并采用三维扫描测量方法高效地获取全息数据,对分离的散射场进行了研究,有利于提高声场重建的抗干扰性。
整体来看,边界元算法可以用于不同形状声源的声场重建,其有限元分析问题的思路,很适合工程实际应用。但该方法在边界元划分、奇异积分求解以及正则化问题中存在一些问题,特别是对于大型设备的表面声场重建时,大量的边界元划分导致运算量激增,导致算法运算量增大。
2.3 等效源算法
对于复杂形状声源体的声场重建而言,为了避免边界元算法因划分大量单元格导致的巨大运算量以及复杂运算,等效源算法提供了一种相对简洁的方法,其主要运用等效的思想,在声场辐射源的内部,用若干简单源激发的声场叠加来等效拟合原本的声场[32],将声场重建问题转化为求解等效源强度,并通过传递矩阵来重建空间声场。Jeon和Ih[33]通过分析声场等效的原理,严格推导声场等效重建的公式,得到了基于等效源方法的近场声全息算法,将ESM与边界元方法对比,重建结果表明ESM在传感器数量上明显少于逆边界元法,且运算过程简单便于工程化。其基本原理如图2所示。
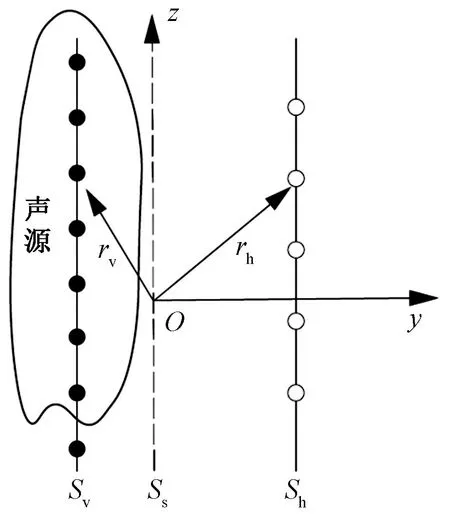
O为直角坐标系坐标原点;rv和rh均为位置矢量,表示空间位置;Sv为等效声源面;Ss为声源面;Sh为全息测量面图2 等效源方法原理图
假设传感器阵列有M个阵元传感器,声源内设置N个等效源。测量面上的声压Ph可以表示为
Ph=GhvQv
(5)
式中:Qv为等效源强度向量;Ghv为等效源与测量面的自由场传感矩阵,矩阵Ghv中元素Ghv(m,n)表示第n个等效源与第m个阵元之间的传递函数。通过求解式(5),得到等效源强度,就可通过到场内任意平面的传递矩阵推导出整个声场的声压分布。声场中任意平面的声压Pr可以表示为
Pr=GrvQv
(6)
式中:Grv为虚拟声源面到声场任意平面的传感矩阵。实际情况中,等效源数目N一般多于阵列的阵元数M,即N>M,此时方程(5)是一个欠定方程,没有特解。
从等效源方法的求解过程中可以看出,该方法的关键是对于等效源强度的求解,也就是对于欠定方程的求解,同边界元方法类似,需要采取合适的正则化处理。传统的等效源方法是采用Tikhonov正则化,但该方法存在过度平滑问题,并不适合等效源强度的求解。考虑到等效源解的形式大多是稀疏的,基于这种稀疏性,Chardon等[34]结合压缩感知技术方法,提出了一种L0范数正则化,提高了等效源强度求解的稳定性;陈汉涛等[35]结合压缩感知技术对低信噪比条件下的声场进行重建,对等效源方法在低信噪比环境中的应用进行了探索;Bi等[36]基于压缩感知原理,采用冗余稀疏基构建等效源,并利用一阶范数最小化约束求解,实现了较好的声场分离效果;Chaitanya等[37]将等效源算法与神经网络算法相结合,采用机器学习模型构建等效源权重系数与测量声压之间的关系,提高了声场重建速度。这些改进方法在实验室环境下取得了不错效果,为提高重建声场分辨率和稳定性提供了新思路。
等效源法所用到的检测传感器相对较少,适合于设备故障的检测。例如,Geng等[38]将插值时域等效源方法运用于重建振动结构的瞬时表面法向速度,为振动体表面速度测量提供了新的方法,不过该方法以半圆形板为对象进行测试,形状相对简单,重建的声像图分辨率也相对较低;Wang等[39]基于等效源方法的声全息建立故障轴承特征频率下的声像图,并采用卷积神经网络的方法对声像图进行特征学习和故障分类,可以对运行中的轴承进行在线故障诊断,但需要较长的计算时间,并需要大量数据训练建立故障判断模型;Wang等[40]利用等效源重建声场的稀疏性,采用广义凹面极值作为惩罚项对等效源强度的求解进行正则化处理,提高了算法在重建过程中的声场重建精度,并提出一种交替方向乘子法的计算方法,优化了算法计算步骤;Yu等[41]将近场声全息方法应用于变压器放电故障的定位,基于等效源原理先通过贝叶斯规则估计,利用期望最大化算法进行优化避免背景噪声的干扰,对变压器放电故障进行可视化,取得了不错的故障诊断效果。这些研究探索性地将等效源算法应用于工程实际,能够实现对噪声源的识别,并基于声像图对设备状态进行分析,但由于成像算法的不足,对于实际设备的故障诊断还有待改进。
2.4 Helmholz方程最小二乘法
HELS算法并不寻求解出方程(1)的精确解析解,而是利用一组适当的基函数组合来近似求解方程,并通过最小二乘法得到最小误差意义下的权重系数[42],再利用近似解的形式来推算声场其他位置的声压,实现声场的重建,将近场声全息问题转化为求解基函数系数的问题。该算法计算过程的复杂度相对降低,有利于工程实践应用,但对于基函数以及展开项数的选择有一定的要求。
HELS算法的基本原理是,将方程(1)的解表示为如下线性组合的形式,即
(7)
式中:ρ、c分别为声场中介质密度和声速;Cj为权重系数;Ψj(r)为基函数;J为基函数展开项数。基函数需要满足方程(1)并且有界,一般是选择该方程的特解,同时为了便于求解,可以根据实际声源形状选择不同的坐标系进行求解,特别是Isakov和Wu[43]为HELS方法在任意表面上重建声场提供了一个严格的数学证明,表明Helmholtz方程的任何辐射解都可以用一组特殊解来近似,为该方法对任意形状声源的声场重建奠定了理论基础。
对于权重系数的求解,可通过矩阵方程(8)得到
(8)
之后便可通过计算声场重建面上的基函数矩阵Ψr,以及得到的权重系数,利用方程(7)得到声场重建面上的声压。
HELS算法从理论基础上就是一种为解决实际工程需要而研究的方法,求解过程中选择一组合适的基函数是至关重要的,到目前为止还没有一组通用的基函数可以用于各种不同形状声源的声场重建,通常需要一定的先验知识,根据声源形状特点选择合适的基函数。通常选择平面波、柱面波和球面波的基函数。由于该方法是通过线性叠加来近似实际声场,对于声源形状长宽比例较大的声场,该方法的重建效果不太理想,计算中的收敛性较差。
在声场重建过程中,基函数的展开项数直接影响声场重建的工程精度。理论上,基函数的展开项数越多,方程的计算越准确,近似解的精度越高。但为了保证方程(8)求解的正定性,会增加更多的传感器测量声场声压,这会导致运算量的增加;同时实际测量中难免会存在误差,这些输入误差也会随着基函数项数的增加,使重建声压的准确度越来越低,通常采用迭代对比的方法获得最优展开项数[44],但迭代法求解过程需要多次重复求解,算法的重建效果并不是很好。
对于HELS算法来说,声场重建中的传递矩阵就是由不同测量点上的基函数展开项构成的,实际上对于最佳项数的选择就是一种正则化求解的过程。Natarajan和Wu[45]采用奇异值分解方法(singular value decomposition,SVD)分解截断奇异值求解,并结合Tikhonov方法提出采用一种混合正则化的方法求解最优展开项数,改进了高模态声场重建的准确性,但这种方法在求解过程中仍需要通过最小二乘法反复迭代,计算过程比较复杂;Cheng等[46]提出一种截断奇异值分解与吉洪诺夫正则化相结合的正则化方法,保留截断奇异值分解(truncated singular value decomposition,TSVD)截断点前的大奇异值,其余小奇异值的高频噪声通过Tikhonov正则化进行修正,改进了算法的重建效果。
HELS方法通过等效近似的方法来解决实际工程中大量数据运算的问题,具有测量传感器少的优点,在实际故障检测中应用较多。Chen和Wu[47]通过将声源部分表面法向振速和近场声压数据作为输入量,按照HELS方法原理重建声源结构表面振速,能够有效提高重建声源表面振速的精度,并用钢板振动进行了测试验证,质点振速的采集相较复声压而言,不受传感器间距影响,低频特性优越;Xu等[48]针对无人机、直升机等旋翼产生的气动噪声进行研究,声场再现方法与最优统计方法在声模态空间中的一致性,将两者结合提出一种全局主动噪声控制方法,对全局噪声控制有较好的效果,给出了优化阵列传感器配置的思路;Mathews等[49]基于最小二乘法的近场声全息方法,重建了美国空军的波音/萨博T-7A红鹰喷气式教练机上F404-GE-103涡扇发动机喷管后缘的声场,研究发现在不同推力工况下显示出不同的声场特性,分析不同噪点极值的产生原因,为大型机械设备的声学检测提供了借鉴。
HELS方法的优点是公式简单、计算效率高、应用灵活,而且HELS方法直接求解亥姆霍兹方程,避免了积分运算,不存在边界奇异积分的问题,而且它不受基于边界元的Helmholtz积分公式固有的非唯一性问题的影响,但在基函数的选择和最优展开项数的选择上仍需要不断改进。
3 结论与展望
通过近场声全息获得准确可靠的声场图像是声学故障诊断的基础,而近场声全息技术的发展一方面在于高性能的传感器阵列对声场信息的有效采集,另一方面就是准确、稳定、高分辨率的算法,这两者是相互关联、相互影响的。例如,传感器阵列的设计要基于算法的特点,为算法提供有利于声像重建的数据,并且尽可能采用少量的传感器采集声场信息。在本文中主要介绍了4种相对完善的近场声全息算法,分析了它们的特点和不足,以及工程应用的现状。
目前看来,各类近场声全息算法并不完善,还存在故障声源定位误差较大、声场重建频率有限、重建声场分辨率受限、复杂形状声源重建困难等方面的问题,对于广泛的实际工程应用还存在一定差距。不过,随着数据信息处理技术的快速发展,以及先进的传感器采样和处理技术,近场声全息技术的研究方向有以下几个方面。
1)深入研究声场空间中传感器的排布方式以及信号采样方式,高效采集声场信息。从本质上来讲,近场声全息技术就是希望能尽可能利用较少的传感器准确采集声场信息,并通过一定方式的数据处理,实现较高分辨率的声场重建。对于传统测量中采用大量传感器的整齐排布往往会带来大量的冗余数据,也就导致算法的处理数据量的增加,严重影响了算法的运算效率。应当结合信号处理技术中的稀疏采样技术,研究不同声场环境的时空采样方式,合理设计传感器的声场排布方式,减少声场采样数据。
2)探究实际声场中的传递函数,提高算法的抗干扰能力。对于不同近场声全息算法而言,主要区别在于对声场传播的理解不同。BEM是将Helmholtz积分公式离散化处理,转化为矩阵方程求解;ESM是将声场看作多个单极子声场的叠加;HELS是将空间声场中的声压是基函数的线性组合。这些方法都将声场的重建过程转化为矩阵方程的求解,只是构建传递矩阵的方式互不相同。目前传递矩阵的构建都是基于自由场建立的,应当从实际声场环境出发,考虑环境混响等影响,探索构建符合实际的传递函数,增强算法可靠性。以及研究利用神经网络等机器学习算法,计算测量声压或振速与权重系数的关系,通过训练数据建立合适的机器模型,直接获得算法的传递函数。
3)在近场声全息重建过程中,由于方程的欠定性,很容易受到输入数据的误差影响,需要一定的正则化处理方法。但传统的正则化方法会损失高频信号,影响重建分辨率,为了能够使高频信号成分重建,还需要较多的传感器采集数据来弥补,反而增加了运算成本。从声源传播的稀疏性出发,考虑结合稀疏采样原理以及贝叶斯原理等方法,探索适合重建算法的正则化方法。
4)当前基于近场声全息的故障模式识别研究相对较少,对于实际设备的故障诊断应用不多,应当借鉴模态特征诊断的方法,探寻近场声全息图谱的特征模态,找出不同故障情景下的特征图谱或特征矩阵,并结合机器学习等方法提升故障诊断效率,逐步应用于分析设备复杂声场的故障诊断。
