基于MATLAB 的大地测量计算实验系统设计与实现

刘 军，王 鹤

（1.防灾科技学院 生态环境学院，河北 燕郊 065201；2.防灾科技学院 地球科学学院，河北 燕郊 065201）

目前已有的大地测量计算实验系统一方面偏重实验仪器模拟操作，大地测量数据处理功能不够突出，另一方面源程序不开放，导致学生难以再利用，进而难以开展创新性实验[1]。

鉴于上述原因，在充分考虑人机交互的友好性和可扩展性的基础上，采用实验系统开发中常用的MATLAB软件[2-5]，通过系统功能模块的划分、用户界面的设计、算法公式的梳理及程序代码的实现等步骤，设计开发了一套大地测量计算实验系统。该系统可用于大地测量计算内容的课堂教学演示，提高授课效率，激发学生的学习兴趣，为学生提高动手能力和创新能力提供平台基础，达到提升教学质量的目的。

1 系统总体设计

1.1 系统设计思路

根据大地测量学课程理论教学的重点并结合工程实践的需要，大地测量中基本计算内容应涵盖参考椭球与测量计算、高斯投影及其计算、大地测量坐标系统的转换等3 个方面。这些内容间既相互关联又彼此独立。基于上述思考，基于MATLAB 的大地测量计算实验系统集成了3 个经典功能模块，每个模块中均含有不同的子模块，如图1所示。

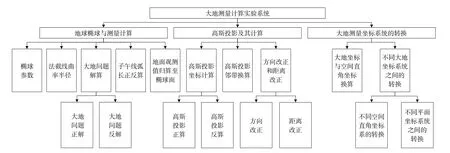
图1 大地测量计算实验系统功能模块

1.2 开发平台与主界面设计

实验系统选择功能强大的MATLAB R2015b 作为开发平台。MATLAB 是由美国MathWorks 公司开发的科学与工程计算软件，具有功能强、效率高、简单易学等特点，尤其是矩阵计算，省时直观，适用于理论教学过程中展示计算实例，辅助理解理论公式的计算过程，可以改善理论课程的教学效果，使学生更容易掌握抽象概念和复杂运算。

MATLAB 的GUI 设计可通过2 种方法实现。一种是编写M文件创建GUI，另一种是通过GUIDE工具设计界面。本系统采用GUIDE 创建界面，新建的MATLAB GUI保存成包含交互控件和菜单属性的二进制fig文件和用来存储回调函数的M文件。通过编写界面中各个交互组件和菜单的回调函数，实现界面设计效果和程序功能。

用户界面设计，力求简洁、清晰地体现系统的主要功能和特征[3]。系统的主界面包括地球椭球与测量计算、高斯投影及其计算、大地测量坐标系统的转换等3 个功能模块，点击主菜单可弹出对应的二级菜单。通过点击子菜单或工具栏进入各功能子模块对应的界面。

2 系统功能模块实现

2.1 参考椭球与测量计算模块

大地测量学中研究的地球形状主要是指大地水准面的形状，它是一个封闭的不规则重力等位面[6]，是野外测量作业的基准面。为了解决测量计算问题，需要一个可以代表地球形状和大小的规则数学曲面，这就是具有几何特征的参考椭球面，通过建立地面与椭球面上点的一一对应关系，从而开展以椭球面为基准面的一系列大地测量计算研究。参考椭球与测量计算模块包括5 个子模块：椭球参数、法截线曲率半径计算、子午线弧长正反算、地面观测距离归算至椭球面和大地问题解算。

椭球参数是描述参考椭球形状和大小的几何参数，包括长半轴a、短半轴b、扁率f、第一偏心率e和第二偏心率e′等。地球曲率半径是大地测量和地球科学计算中常用的基本参数，主要包括主曲率半径（子午圈、卯酉圈方向）和平均曲率半径。子午线弧长是大地测量学中的一个基本量，主要用于研究地图投影中的高斯投影计算和推算地球形状大小的弧度测量计算。地面观测距离归算至椭球面，即斜距归算，是指将野外实测的电磁波测距边长在经过气象改正（温度、气压、湿度）、仪器常数改正（加常数、乘常数）、周期误差改正等系统误差后得到的仪器中心至反射镜中心的空间直线距离D归算到参考椭球面上2点间的大地线长度S。大地问题解算分为大地问题正解和大地问题反解。随着现代空间技术和航空航天、船舶导航、导弹制导等方面科学技术的发展，大地问题解算（尤其是反算）有其重要作用。鉴于各种用途和大地问题解算的复杂性，大地问题解算的方法和公式多达几十种。这些算法中，比较典型的有高斯平均引数公式、贝塞尔（Bessel）公式和韦森特（Vincenty）[7]公式。其中，高斯平均引数公式是解决短距离（<200 km）大地问题解算的一种经典方法，大地坐标计算精度为0.000 1″，方位角计算精度为0.001″，大地线边长精度为0.001 m。贝塞尔公式展开为椭球偏心率平方e2（或e’2）的幂级数，解算精度与距离无关，适用于中长距离（400~20 000 km）的大地问题解算[8]。韦森特公式适用于大地线长从1 cm 到近20 000 km 的大地问题解算，大地方位角的精度为0.000 1″，大地线长的计算精度为毫米级。该实验系统只提供了高斯平均引数公式和贝塞尔公式的计算，学生可参考相关文献实现韦森特公式的编程，扩展系统内容，从而锻炼动手能力。

以子午线弧长正反算模块为例，包括输入参数、执行按钮和计算结果3 部分。该模块能够实现子午线弧长正算，即根据纬度B计算子午线弧长X，也可以根据子午线弧长反求大地纬度B，即子午线弧长反算。用户选择坐标系统（如CGCS2000），输入大地纬度B（DD.MM.SSSSS 格式），点击“正算”按钮，计算子午线弧长X。输入子午线弧长X，点击“反算”按钮，计算大地纬度B，与给定大地纬度B对比，验证反算程序的正确性。如果需要计算的子午线弧长X或大地纬度B较多，可采用文件批量转换方式，在选择坐标系统后，点击“文件形式”按钮，即可完成批量计算，以文件形式保存计算结果。用户点击“数学模型”按钮，可以查看子午线弧长正反解公式，分别为式（1）、（2）。

大地纬度B处的子午线弧长计算公式：

式中，B为大地纬度（单位：弧度）；为第一偏心率；a为长半轴；b为短半轴。

子午线弧长反求大地纬度B的迭代计算公式：

2.2 高斯投影及其计算模块

由于椭球面上的大地坐标不能直接控制大比例尺测图，也不能直接作为工程测量的控制。此外，在椭球面上的大地问题计算非常复杂和繁琐。因此，为了满足控制地形测图及控制网计算简便的需要，须利用高斯投影的方法进一步把椭球面上由大地线构成的三角网归算成高斯平面上由直线段连接而成的平面三角网[9]。高斯投影及其计算模块包括5个子模块：高斯投影正算、高斯投影反算、高斯投影邻带换算、方向改正与距离改正。

高斯投影（又名等角横切椭圆柱投影）是高斯-克吕格投影的简称，是地球椭球面到平面上正形投影的一种，是我国采用的投影方法。高斯投影坐标计算包括高斯投影正算和高斯投影反算。高斯投影正（反）算的推证方法有待定系数法和复变函数理论方法[10]。其中，待定系数法是利用该投影的3 个条件，将其展开为经差（横坐标）实数型幂级数形式，具有容易理解和直观的优点，但公式冗长复杂；利用复变函数理论推导的高斯投影公式具有形式紧凑、公式简单、计算效率高等优点[11]。工程中为限制高斯投影的长度变形，必须将椭球面依中央子午线按照经差3°带或6°带进行分带投影，形成了各带独立的高斯平面直角坐标系。为解决生产实践中不同投影带之间测量成果的转换和联系，需要将一个投影带的高斯坐标换算到相邻带的高斯坐标，称为高斯投影邻带换算，其基本思想是把椭球面上的大地坐标作为过渡坐标，利用高斯投影正、反算公式进行换带计算。方向改正，又称曲率改正，是椭球面上的两点间的大地线方向归算至平面上相应投影点间的弦线方向所加的改正。本实验系统实现了适用于三、四等三角测量的近似公式及二等三角测量的较精密公式的计算。距离改正是将椭球面上的大地线长S改化为平面上投影曲线两端点的弦长D所加的改正，根据高斯投影长度变形公式可知，离开中央子午线越远，长度变形越多，距离改正也就越大。

以高斯投影正算模块为例，点选列表框坐标系统（如1980 西安坐标系）后，按度分秒格式分别输入大地经度L和大地纬度B，然后选择投影带类型（如6°带），点击“计算”按钮，即可获得高斯平面坐标、点位所处带号和子午线收敛角。点击“数学模型”按钮，可以查看高斯投影正算的理论模型[16]。

式中，X为子午线弧长；为卯酉圈曲率半径；l=L-L0（单位：弧度）为经差；L为大地经度；L0为中央子午线经度；t=tanB；为第二偏心率；B为大地纬度；为第一偏心率；a为长半轴；b为短半轴。

2.3 大地测量坐标系统的转换模块

我国常用的大地坐标系统包括1954 北京坐标系、1980 西安坐标系和2000 国家大地坐标系（缩写为CGCS2000）[19]，在工程测量实践中通常需要将不同大地坐标系统之间进行转换。大地测量坐标系统的转换模块包括3 个子模块：大地坐标与空间直角坐标换算、不同空间直角坐标系的转换和不同平面坐标系统之间的转换。

同一参考椭球下地面或空间一点P 可以表示为大地坐标（B，L，H）和空间直角坐标（X，Y，Z），它们是同一大地坐标系统下2 种不同的坐标表达形式，二者可通过大地坐标与空间直角坐标换算公式实现换算。不同参考椭球下定义的不同大地空间直角坐标系统之间可采用布尔莎七参数模型实现坐标转换。不同大地坐标系统下高斯平面直角坐标之间可通过相似变换模型（赫尔默特法）和多项式回归模型实现坐标转换。

以大地坐标与空间直角坐标互换模块为例，该模块可以实现单点和文件形式的大地坐标和空间直角坐标之间的相互换算。点选列表框坐标系统（如1954北京坐标系）后，分别点击“大地转空间坐标”和“空间转大地坐标”按钮可实现大地坐标（B，L，H）和空间直角坐标（X，Y，Z）之间的互换。点击“数学模型”按钮，可以查看大地坐标与空间直角坐标互换模型[13]，即：

式中，L为大地经度；B为大地纬度；h为大地高；为卯酉圈曲率半径；为第一偏心率；a为长半轴；b为短半轴。

3 实验系统特点与应用

该实验系统具有以下特点：①界面友好，操作简便。系统模块化设计，各模块功能的划分具有条理化，界面层次分明；②良好的交互性。通过设置不同参数（如坐标系统、算法模型、投影带号）观察实验计算结果的不同，减少重复编程的时间。能够通过“数学模型”按钮查阅计算程序应用的理论公式，人机交互友好；③可扩展性强。由于算法源代码开放，方便具有大地测量学知识与MTALAB编程基础的学生对程序进行修改完善，优化扩充功能模块，锻炼学生使用理论知识与计算机解决实际问题的能力，提高个人素质。

该实验系统已经应用在我校测绘工程专业基础课大地测量学的辅助性教学中。在课堂教学中，教师在理论讲授和公式推导后，结合工程算例，从应用出发，把理论内容和实际应用密切结合，利用实验系统直观演示计算过程，强化公式中各符号（如椭球参数、不同曲率半径、各种纬度等）的含义，使学生加深对基本原理的深刻理解，提高了学习兴趣；学生利用该实验系统开展课后自主学习，对理论知识进一步消化与吸收，提高了学习效率，充分调动了学习的积极主动性。鼓励编程能力较强的学生通过查阅文献开拓视野，研究改进算法，开展创新性实验，扩充功能模块，激发和培养了学生的实践创新能力。此外，在大地测量学课程设计和生产实习中，使用本系统的“高斯投影坐标计算”、“高斯投影邻带换算”和“不同大地坐标系统之间的转换”等模块功能开展测量数据的分析、处理和计算工作。

4 结 语

本文从测绘工程专业应用型创新人才培养和《大地测量学》课程教学需求出发，注重理论内容与实际应用密切结合，基于MATLAB设计开发了大地测量计算实验系统，实现了参考椭球与测量计算、高斯投影及其计算、大地测量坐标系统的转换等大地测量学基础计算功能，软件界面友好，操作简便，可扩展性强。实践证明，该实验系统可全面辅助大地测量学课程的教与学，提高了大地测量学的授课效率，充分调动了学生自主学习的积极性，改善了课程教学效果，对激发和培养学生的工程实践创新能力有较大帮助。