基于滑动窗口和置信度的无线传感器网络异常检测算法*
2024-01-09车丽娜任秀丽
车丽娜,任秀丽
(辽宁大学信息学院,辽宁 沈阳 110036)
无线传感器网络(Wireless Sensor Network,WSN)由大量小型的传感器节点组成,具有数据感知、数据收集、数据处理和无线通信的功能[1]。传感器节点通常较小且造价低廉,可密集分布在完全随机化的地理区域中,在环境监测、农业生产、工业制造和军事探测等领域有着广泛的应用[2-3]。由于传感器节点随机分布在户外环境中,可能会受环境波动、入侵攻击或硬件故障的影响,使传感器节点读取到异常数据,其产生原因通常很复杂,不及时处理可能会引起信息误报,产生额外开销。因此,做好无线传感器网络的数据异常检测,及时诊断异常值的来源,对于管理者进行控制决策尤为重要[4]。
异常值的检测方式大致可分为集中式检测和分布式检测,主要的数据异常类型有两种:事件异常和错误异常[5]。针对这两种数据异常类型,目前有大量文献做了深度研究。文献[6]通过计算待测节点与可靠邻居节点的相似性进行异常数据检测,通信开销较大。文献[7]通过比较待测节点中异常值数量与滑动窗口的大小关系进行事件检测,检测周期过长致检测效率低下。文献[8-10]提出节点信息可靠度,选出可靠节点,利用贝叶斯模型对检测结果综合决策,节点间通信开销较大。文献[11]根据节点收集数据量的大小在本地自适应地进行异常检测,但未明确其参数的取值范围。文献[12-13]基于特征分类检测时间序列中的异常数据,难以详细地描述原始序列的局部动态,致检测精度较低。文献[14-15]通过建立异常预测模型,计算预测值与测量值之间的差值是否超过预定义的异常阈值,通信开销小,但检测误差指数并没有显著降低。文献[16]提出了基于预测机制的事件检测容错算法(K-Nearest Neighbor-Particle Swarm Optimization-Extreme Learning Machine,KNNPSOELM),通过收集不同时刻待测节点的节点状态,利用时空相关性对异常数据类型协同判断,能耗低但在空间相关性检测中仅考虑了节点间的距离因素,导致检测精度降低。文献[17]提出了一种基于邻域的离群值检测算法(Outlierness Factor Based on Neighbourhood to Detect and Analyse the Outliers in Sensor Network,OFN),采用邻居的异常因子值,联合节点间的通信概率完成自身检测,算法太过于依赖邻居节点的数据信息,处理全部邻节点所收集的数据将造成较大的计算开销,致节点能耗较大、网络寿命缩短。
以上提到的异常检测算法均未考虑到监测区域内环境因素对检测结果判定带来的不确定性影响,导致算法容错性能较差、检测精度较低。本文提出的基于滑动窗口和置信度的无线传感器网络异常检测算法(Anomaly Detection Algorithm Based on Sliding Windows and Confidence,ADABSWC),综合考虑环境因素及检测结果的差异性,利用环境因子量化监测环境中的不确定性,得到环境因子的置信区间。参照其区间取值建立异常数据干扰区间,用于识别滑动窗口数据序列中的异常数据。根据所提出的数据异常度的计算方法,预判异常数据的类型;然后,利用相对熵计算节点信息置信度。根据置信度得到不同的决策信息,对节点事件异常类型做出最终判定。该算法检测精度高、误报率低且减少了节点间的通信次数,降低了节点的能量损耗。
1 网络模型
假设N个传感器节点被随机地部署在待监测区域内,节点间自组织形成网络,且网络中的节点满足以下条件:①各个节点负责数据的收集与处理,且具有相同的处理能力;②各个节点具有唯一标识,通过定位设备反馈自己的位置信息;③节点的最大通信半径R、广播半径r均相同,且时钟是同步的;④相同采样周期内,正常节点收集到的数据服从正态分布[18]。
时间序列是无线传感器节点采集数据的重要形式,可以表明环境的变化特征。传感器节点在连续一段时间内,检测到的数据显著偏离于正常数据,便认为有异常发生[19]。异常值的来源主要包括:①事件异常:传感器节点所在区域发生了特定事件;②错误异常:传感器节点由于自身的软硬件故障或能耗问题而无法正常工作。
2 基于滑动窗口和置信度的异常检测算法
本文提出的无线传感器网络异常检测算法主要分为两个阶段:第一阶段是基于滑动窗口模型得到数据差值序列均值的区间估计,建立异常数据干扰区间,通过计算数据异常度预判节点异常类型;第二阶段利用相对熵计算节点信息置信度,协同可靠的邻节点确定节点数据异常源自事件。
2.1 预判节点的数据异常类型
传感器节点收集的环境数据具有连续性,而节点本身的存储能力有限,无法满足数据序列的无限增长性,故本文采用滑动窗口模型(Sliding Window Model)处理数据,节点仅保存最新的k个数据。滑动窗口中的数据遵循先进先出的规则,假设当前窗口数据集为{r(t1),r(t2),…,r(tk)},其中r(t1),r(t2),…,r(tk)分别为t1,t2,…,tk采样时间下采集到的数据。当新数据r(tk+1)到来时,窗口向前滑动,窗口中的数据集更改为{r(t2),r(t3),…,r(tk+1)},以此类推。
传感器节点对同一监测区域内多个设备引起的干扰现象非常敏感,据此提出环境干扰因子η来衡量监测环境的不确定性。假设在某一个采样周期T内,传感器节点j采集的数据集为Dj(ti)={dj(t1),dj(t2),…,dj(tk)},其中数据量为k,对数据集中的数据进行如下预处理:
每两个连续采样值之间的差值用Δdv表示,其数据序列为,数据量个数n=k-1,利用式(3)、式(4)计算差值序列的样本均值和样本方差。
设Δdv的总体服从正态分布N(μ,σ2),由于总体的方差σ2未知,因此使用差值序列样本方差S2来估计总体差值样本均值的置信区间,可得到:
得到T关于总体均值μ的枢轴量:
得到置信度为1-α的总体差值序列均值μ的区间估计:
因此,得到环境干扰因子η的取值区间来衡量监测环境的不确定性。令区间的下限为环境干扰因子η的最小值ηmin,区间的上限为环境干扰因子η的最大值ηmax,其中α和k的取值将在实验中给出。
由于传感器节点部署于不同的环境中,节点分布的规模不尽相同,其射频干扰、电磁干扰的程度也会不同,测量值会出现上下波动的现象。在有些环境中,即使数据波动较大,数据也是正常的;而有些环境中数据波动较小,数据却是异常的。因此,异常检测中将事件阈值设置为一个固定值是不可靠的,利用传统的阈值函数进行判断时容易产生漏报或误报。考虑到异常检测方法的差异性,为更好地提高算法的容错性能,在事件阈值函数的基础上,结合环境干扰因子η,建立异常数据干扰区间[LL,UL],如式(9)所示。可对环境中的不确定性因素所引起的数据波动进行容错,提高识别异常值的能力,从而减少误报、漏报的次数。
式中:k为样本规模;δ为样本标准差。Rth(t)表示事件阈值函数[20];Ee(t)表示正常工作的传感器在事件区域内测量值的数学期望;En(t)表示正常区域中测量值的数学期望。
为了进一步判断数据异常类型,本文引入以下两个概念,给出定义如下:
定义1数据异常度θ:对于数据样本点dj(ti),其数据异常度θ表示采样数据dj(ti)与事件阈值Rth(t)之间的差值偏离于异常数据干扰区间的程度。公式如下:
式中:dj(ti)为传感器节点在ti时刻的读数;UL(Upper Limit)为干扰区间的上限;LL(Lower Limit)为干扰区间的下限;AD(Abnormal Data)为异常数据;ND(Normal Data)为正常数据。θ越大说明传感器节点监测的测量值离正常样本数据越远,dj(ti)为异常值的可能性越大。
由此得到一个采样周期内,数据异常度θ的平均值μ(θ):
定义2事件异常指标φ:依据异常数据干扰区间,得到判断是否发生事件异常的重要指标。公式如下:
实际中,异常值的情况可分为高于正常值的异常(AD>ND)或低于正常值的异常(AD<ND)。若异常值大于正常值时,则将异常数据干扰区间的上限作为识别异常数据的标准。数据异常度θ以及事件异常指标φ分别采用式(11)和式(13)中AD>ND条件下的计算方法;同理,若异常值低于正常值时,将异常数据干扰区间的下限作为识别异常数据的标准。数据异常度θ及事件异常指标φ分别采用式(11)和式(13)中AD<ND 条件下的计算方法。
因预判节点数据异常类型时,以上两种情况的判别流程均相同,仅数据异常度θ及事件异常指标φ所采取的计算方法不同。本文对算法的流程及流程图进行相关描述和绘制时,仅考虑异常值大于正常值(AD>ND)的情况。当测量值dj(ti)>Rth(t)+或dj(ti)=dj(ti-1)时,说明节点出现了异常。为判断异常数据的类型,需计算数据异常度θ和事件异常指标φ,在一个采样周期内,计算采样周期内数据异常度的均值μ(θ)。若μ(θ)>φ且dj(ti)≠dj(ti-1),则认为该节点异常源自事件。若μ(θ)<φ或dj(ti)=dj(ti-1),则认为该节点异常源自错误,并将判断结果发送给基站。
在本文提出的基于滑动窗口和置信度的异常检测算法中,其预判节点异常类型的流程,如图1 所示。本算法利用滑动窗口模型,考虑到监测环境中的不确定性,提出环境因子建立异常数据干扰区间,可以避免在异常数据识别过程中因测量误差、通信干扰带来的误报,提高了识别异常数据的能力及节点异常类型的检测精度。虽然依靠滑动窗口模型可以检测到事件异常的发生,但凭借单个节点的检测结果并不可靠。考虑到同一监测区域内的传感器节点具有空间相关性,物理位置相近的节点在同一采样周期内采集到的数据具有相似性。因此,利用相对熵来计算节点信息置信度,通过引入多通信半径划分可靠邻域,利用可靠邻居节点的信息对本节预判出的事件异常类型做进一步的检测。
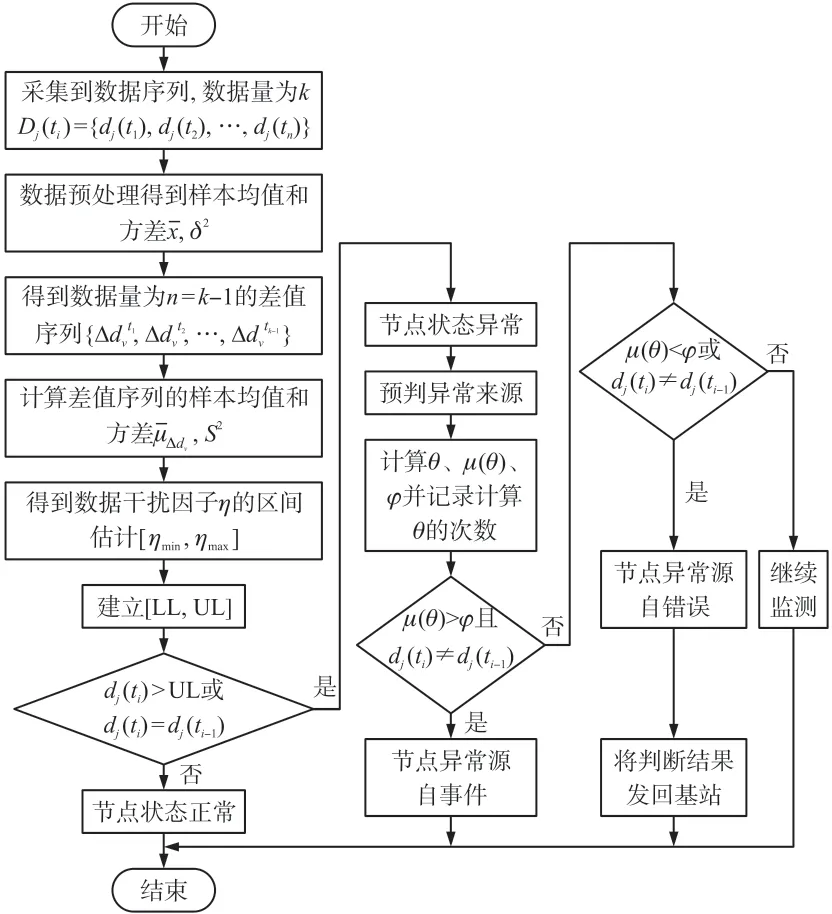
图1 预判节点异常来源算法流程图
2.2 事件异常的确定
传感器节点间的判定原理,源自于传感器节点在物理位置上的分布情况,在相邻区域内测得的数据具有连续性和相似性。在空间关系中,节点间的空间相似性不仅与物理距离有关,还与节点间采集信息的相似程度有关。为了反应异常节点与其邻居节点间的关联程度,本文引入相对熵[21]计算两组数据随机变量分布间的相关性,用于计算节点信息置信度,以此进一步确定事件异常的发生。
2.2.1 节点信息置信度
在2.1 节中已经被预判为事件异常的传感器节点j,其通信半径R内所有邻居节点的集合,即Neighbor(j)={S(i)|dist(i,j)≤R},节点的个数记为Nj。利用邻居节点i∈Neighbor(j)间的距离参数反映对事件异常节点决策的贡献度wij:
所有邻居节点的加权和为1。
假设异常节点j和其所有邻居节点在同一采样周期T内,收集到数据量为k的数据序列分别为:
式中:Rj(t)表述异常节点j收集的数据序列;(t)表示异常节点j的邻居第i个邻居节点收集的数据序列。
对式(15)中所采集到的数据序列分别进行归一化处理:
设P(xj)、Q(xi)分别为异常节点j与邻居节点i进行归一化处理后的概率分布函数,利用相对熵计算公式:
由于相对熵具有非负性、非对称性,熵的大小和两个变量的数据大小没有关系,只与数据变量的分布有关,因此可利用相对熵表示节点间信息相似度τij:
节点间信息越相似,相似程度越高,熵值越小,反之,熵值越大,故对τij取倒数对节点信息置信度进行优化,得到式(20):
式中:λj为节点信息置信度;Neighbor'(j)是与节点j状态相同的邻节点集合;Ni为j的邻居节点;N'(j)是Neighbor'(j)的个数。
当节点j的异常类型被预判为事件异常时,接下来将与其邻居节点协作计算节点信息置信度,进行协同判断。根据节点信息置信度的大小,得到不同的决策信息,从而确定2.1 节中预判的节点异常源自事件异常,使检测结果更加准确。
2.2.2 多通信半径
为减少节点间的通信开销、降低节点能量损耗,本算法引入多通信半径划分最佳邻域,如图2 所示。将节点j的最大通信半径R分成,R,分别对应A、B、C、D,4 个区域。若A区域内节点数量充足,通过式(20)计算得到该区域内邻节点对j节点的置信支持度。若置信度较高,根据距离越近、相似度越高的原则,则2.1 节中节点j检测到事件异常发生的支持率越高,便可确定节点j的异常源自事件。便不再计算其他三个区域的内邻节点对j节点的置信度,并将检测结果发回基站;若A 区域内节点数量较少,可进一步计算B 或C 区域内邻节点对j节点的信息置信度。若区域内节点信息置信度依旧较低,则2.1 节中节点j预判的异常源自事件的支持率越低。故对异常来源判断有误,将进行下一步处理。因此,根据划分的最佳邻域,选择性地计算邻节点信息置信度λj,可减少节点j与其邻居节点间的通信次数,从而降低节点能量损耗,提高检测精度的同时减少了通信开销。
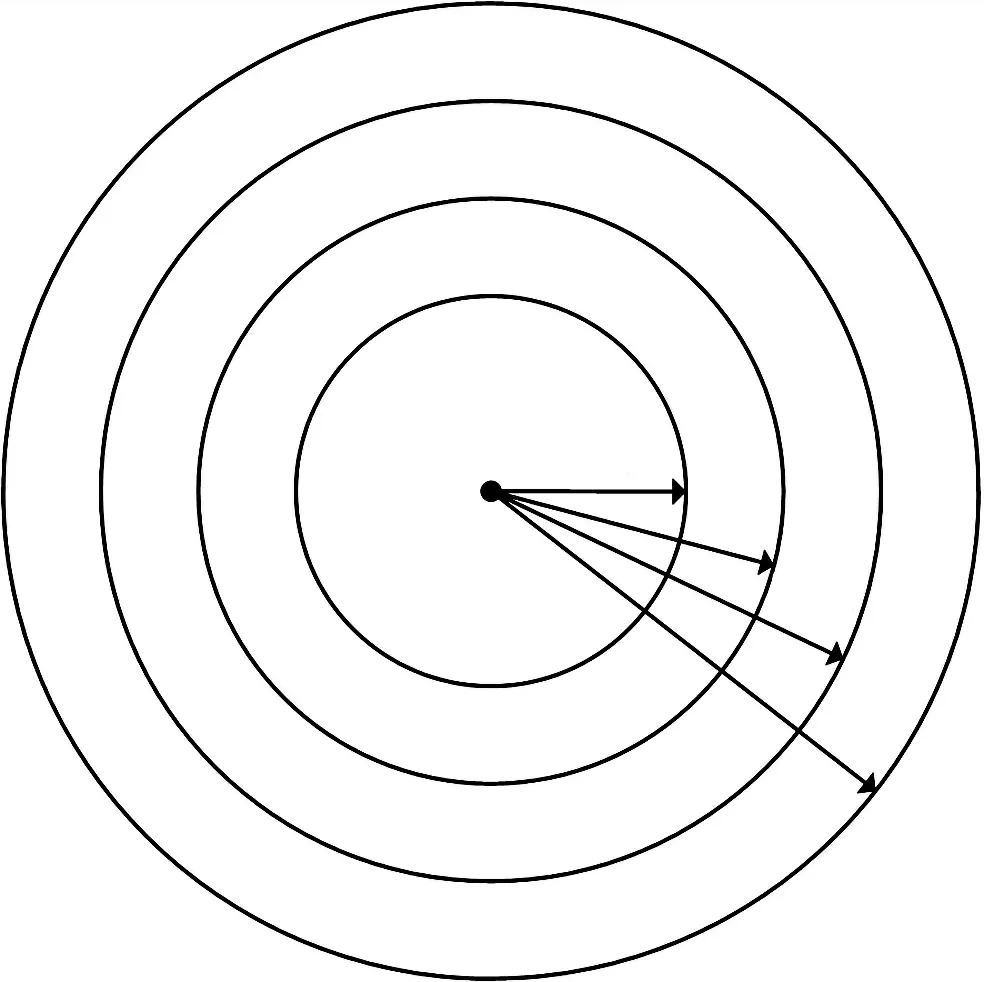
图2 多通信半径示意图
3 仿真实验分析
3.1 实验参数设置
本文使用OMNeT++仿真环境,N∈[200,1 000]个传感器节点随机分布在400 m×400 m 的区域中,节点初始能量均为2 J,通信半径R=20 m。实验假设事件异常集合{r(t)}错误异常随机过程{r'(t)}分别满足r(t)~N(μ',σ'2)和r'(t)~U(En(t),Ee(t)),显著性水平α[22]取5%。
3.2 性能分析
为验证本文算法性能,分别从检测率(Time Positive Rate)和误报率(False Positive Rate)两方面进行分析[23]。
定义2事件节点检测率ETP(C):
定义3事件节点误报率EFP(C):
定义4错误节点检测率FTP(C):
定义5错误节点误报率FFP(C):
式中:E为实际事件节点集合;F为实际错误节点集合;S为监测区域内所有节点集合。
3.3 实验结果及分析
3.3.1 滑动窗口数据量k的取值
滑动窗口数据量k的取值对算法的效率和检测精度会产生较大影响。如果k取值过大,会造成资源浪费影响整体性能;如果k取值过小,会影响检测结果降低检测精度。实验选取无线传感器网络中的光照强度、温度、湿度数据各5 000 组,分别用不同的滑动窗口长度计算方差。滑动窗口长度与数据组方差的关系,见图3。图中数据的方差随着窗口长度的增加逐渐稳定,分析可得k的大小在25 至35 之间较为合适,因此本文k值选取30 用于下文的实验中。
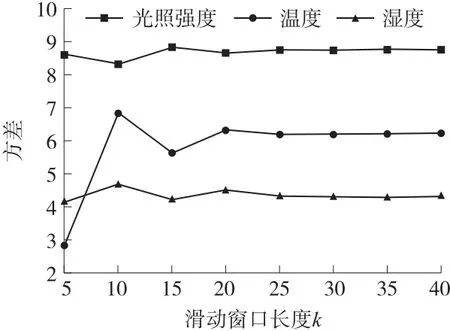
图3 滑动窗口长度与数据组方差的关系
3.3.2 算法的对比实验
现将分布于不同规模下的传感器节点,在错误节点占比(5%)相同的情况下,应用ADABSWC 算法与KNN-PSOELM、OFN 算法进行各种性能的比较。图4所示为事件节点检测率(ETP(C))的变化情况。
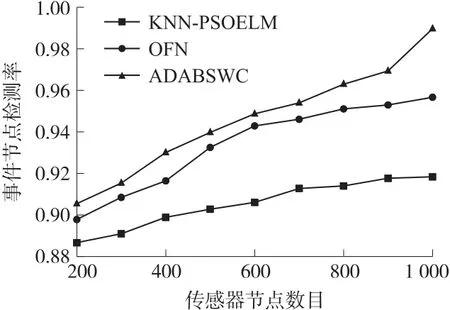
图4 事件节点检测率与节点规模的关系
从图4 可以看出,随着传感器节点数目的增加,KNN-PSOELM、OFN 与ADABSWC 算法的检测精度均有所增加,但ADABSWC 算法事件节点的检测率明显高于其他两种算法,体现出较好的性能。原因在于,ADABSWC 算法在不同的节点规模下,利用环境干扰因子η建立的异常数据干扰区间可对瞬时故障引起的异常数据以及因外部环境波动引起的测量误差进行容错,具有较强的抗干扰能力,提高了算法的容错性能。其次,引入多通信半径划分最佳邻域,减少了传感器节点间的通信开销,降低节点能耗使网络寿命延长,提高了节点处理信息的能力,从而可在不同节点规模下达到较高的检测精度。KNNPSOELM 算法仅考虑了单一阈值,随着节点数目的增加,难以准确判断位于不同地理位置的节点所反应的不同异常类型,容易产生误判,致检测精度较低。OFN 算法虽利用了分布式检测算法的优势,但其异常检测太过于依赖邻节点信息,没有考虑到邻节点信息的可靠性,在传感器节点数目较少的环境下,数据样本较少,表现出较好的性能,而在节点数量较大的环境下,节点所要处理的数据样本增多,计算产生的误差也随之增多,导致检测精度下降。当传感器节点数目达到1 000 个时,ADABSWC 算法的事件节点检测率可达到98.95%,相对于KNNPSOELM 和OFN 算法分别高出7.13%、3.38%。
图5 所示为事件节点误报率(EFP(C))的变化情况。从图5 可以看出,随着传感器节点数目的增加,参与协同判断的邻节点数目增多,三种算法的误报率均有所下降。KNN-PSOELM 算法当节点数据测量值大于阈值Rth(t)时,空间相关性得到提高,虽减少了因瞬时测量值异常引起的误报率,但与OFN算法存在相同问题,即与邻居协作过程中没有排除自身存在错误的节点,导致误报率均高于ADABSWC 算法。ADABSWC 算法对异常节点的状态进行两阶段判断,既考虑到事件的发生与具体时刻无关,而是与事件发生时刻之后的一段时间有关,又考虑到与最佳邻节点进行协作时距离因素及节点间信息相似度对判断结果造成的影响,利用相对熵τij与邻节点贡献度wij对节点信息置信度λj进行修正,有效解决了以往靠单一阈值和无差别邻节点协作对异常来源产生误判的问题,从而大幅降低了节点的误报率。当传感器节点数目达到1 000 个时,ADABSWC 算法的事件节点误报率为1.3%,较KNN-PSOELM、OFN 算法分别降低18.53%、9.8%。
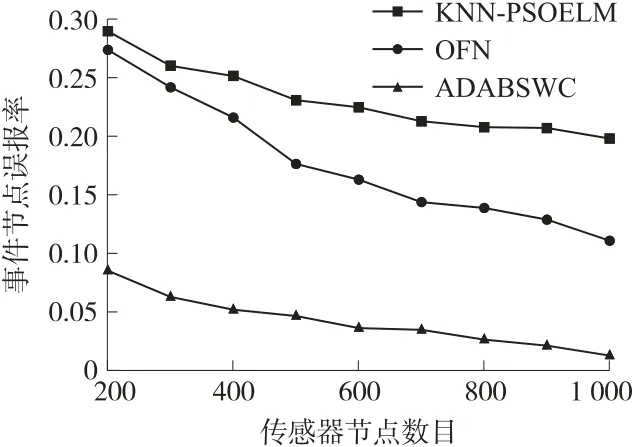
图5 事件节点误报率与节点规模的关系
图6 和图7 所示分别为错误节点检测率(FTP(C))与错误节点误报率(FFP(C))的变化情况。
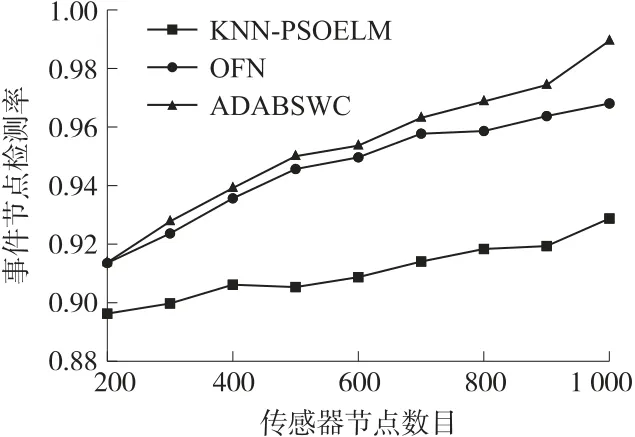
图6 错误节点检测率与节点规模的关系
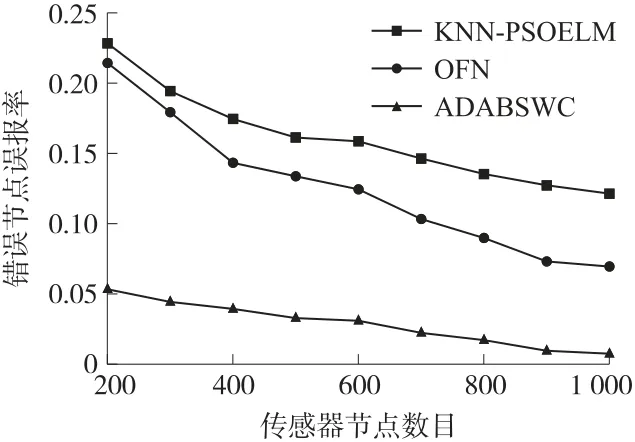
图7 错误节点误报率与节点规模的关系
从图6 可看出,当传感器节点数目小于700 时,OFN 算法与ADABSWC 算法均保持较高的错误节点检测率;当传感器节点数目大于700 时,OFN 算法的错误节点检测率显著低于ADABSWC 算法,原因在于OFN算法根据邻居节点的数据得到离群因子,随着节点规模的增加,待测节点所要处理的邻节点数据量过多,导致待测节点自身能耗过大,致检测精度降低。图6、图7实验表明,随着传感器节点数目的增加,ADABSWC 算法仍保持较高的检测率,较低的误报率,这主要归因于本文算法采用滑动窗口中一段时间的数据,减少了空间错误节点引起误判的情况。当传感器节点数目达到1 000 个时,ADABSWC 算法的错误节点检测率和误报率可分别达到98.96%、0.71%。ADABSWC 算法数据异常来源判断经过两个阶段,对于固定故障或瞬时故障产生的错误异常,具有较好的容错性能,提高了节点异常类型分类的效率及准确性,从而使ADABSWC 算法在不同规模的传感器网络下,均拥有较高的检测精度。
4 结束语
本文提出了一种基于滑动窗口和置信度的无线传感器网络异常检测算法。首先通过滑动窗口模型采集到的数据序列得到差值序列,计算环境因子的取值区间,从而建立异常数据干扰区间识别异常数据。根据提出的数据异常度的计算方法预判节点异常数据的来源;其次利用节点间的空间属性,引入多通信半径划分最佳邻域,选择性地收集邻节点信息,利用熵技术计算节点信息置信度,进行协同判断,最终确定节点异常数据的类型。
