基于改进精细复合多尺度归一化散布熵的生物组织变性识别*
2024-01-09蔡剑华杨江河彭梓齐
刘 备,蔡剑华,杨江河,彭梓齐
(湖南文理学院数理学院,湖南 常德 415000)
现如今,高强度聚焦超声(High Intensity Focused Ultrasound,HIFU)已经被广泛应用于肿瘤治疗[1-3]。相比于传统的肿瘤治疗方法(手术切除、化疗以及放疗),HIFU 治疗具有无创性和安全性等优点。HIFU 治疗是将高强度超声聚焦于肿瘤靶区,使靶区温度迅速上升,当靶区温度超过63 ℃时,靶区位置病变组织的蛋白质出现变性,同时又不破坏靶区之外的正常组织和细胞,实现破坏癌细胞的目的[4-5]。因此在HIFU 治疗过程中,精确检测靶区位置的生物组织是否已经发生变性,是确保HIFU 治疗过程安全高效的关键[6-7]。
迄今为止,HIFU 研究者们尝试从非线性的角度分析HIFU 治疗区域生物组织超声回波信号,发现HIFU 治疗会使组织中超声回波信号的熵值发生变化[8-10]。比如在文献[11]中,多尺度排列熵(Multi-Scale Permutation Entropy,MPE)作为超声散射回波信号的特征被用来区分HIFU 治疗过程中的未变性生物组织与变性生物组织。虽然MPE 具有抗噪能力强,鲁棒性强的优点,但是MPE 方法在分析时域信号复杂度时没有考虑相同排列模式的幅值变化,忽略了时域信号的幅值信息。为了克服上述问题,Azami 等[12]提出了多尺度散布熵(Multi-Scale Dispersion Entropy,MDE)的非线性分析方法。MDE 不仅具有抗噪能力和鲁棒性强的优点,而且在分析时间序列复杂度时包含了信号的幅值信息。在文献[13-14]中,MDE 及其变体被用于HIFU 治疗区域生物组织变性识别,取得了一定的识别效果。但MDE 传统的粗粒化过程是对时间序列进行分段平均值计算,会产生信息丢失的问题;此外随着尺度因子的增加,粗粒化序列的长度越来越短,导致熵值计算结果不稳定且准确性差[15],将影响生物组织变性识别的精度。
针对上述问题,本文对MDE 方法进行了改进,提出了基于改进精细复合多尺度归一化散布熵(Improved Refined Composite Multiscale Normalized Dispersion Entropy,IRCMNDE)的生物组织变性识别方法。IRCMNDE 在MDE 的基础上,引入精细复合多尺度粗粒化算法,然后将粗粒化过程中的平均值计算替换成最大值计算,最后对熵值进行归一化处理,形成IRCMNDE 方法。IRCMNDE 不仅能有效克服MDE 在粗粒化过程中出现信息丢失的不足,提高熵值的稳定性,还能减弱不同参数选择导致的熵值波动。
考虑到IRCMNDE 方法的稳定性和可靠性,结合概率神经网络(Probabilistic Neural Network,PNN)训练速度快,适合实时处理数据的优点[16],本文将HIFU 回波信号的IRCMNDE 值作为生物组织变性特征,然后采用PNN 实现HIFU 治疗过程中生物组织的变性识别。最后与MPE、MDE 以及RCMDE 方法进行比较,说明本文方法的优势。
1 原理与方法
1.1 多尺度散布熵
对于时间序列xn,n=1,2,3,…N,使用正态累积分布函数将时间序列映射为yn,如式(1)所示。
在式(1)中,σ和μ分别为时间序列幅值的标准差和平均值。yn可以通过式(2)映射为从1 到c的集合,c表示类别数目。
在式(2)中,round 为四舍五入的取整函数。然后,如式(3)所示重构嵌入向量。
在式(4)中,Number(πv1,v2,…,vm-1)为πv1,v2,…,vm-1的映射数目,根据式(5),计算散布熵(DE)。
图1 所示为粗粒化过程,根据式(6)得到粗粒化时间序列。
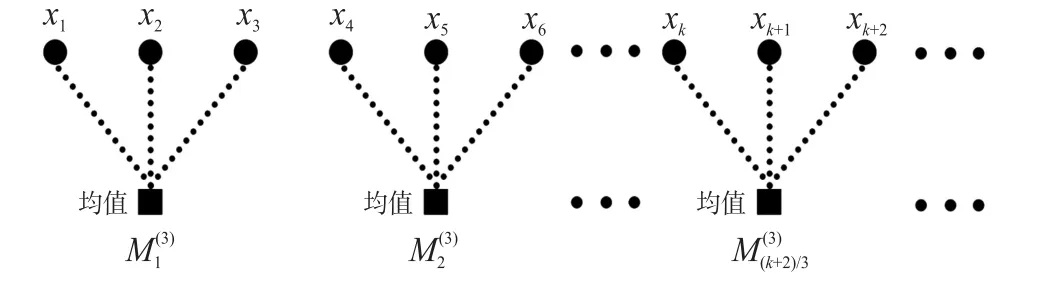
图1 尺度因子τ=3 时的MDE 粗粒化过程
根据式(5)与式(6),多尺度散布熵(MDE)可被定义如下:
1.2 改进精细复合多尺度归一化散布熵
然而,MDE 的粗粒化处理过程是对粗粒化序列进行平均值计算,这容易导致信息丢失的问题。此外,随着尺度因子的增加,粗粒化序列的长度越来越短,导致熵值计算结果不稳定且准确性差。因此,本文在MDE 的基础上引入精细复合多尺度散布熵(RCMDE)。首先对DE 进行精细复合处理,得到RCDE,如式(8)所示。
图2 所示为IRCMNDE 粗粒化过程,将粗粒化过程中的平均值计算替换为最大值计算,以突出信号特征;通过图2 中的粗粒化过程,可得到τ组粗粒化时间序列,避免了粗粒化时间序列中的元素出现丢失的情况,提高了熵值的稳定性,如式(10)所示:
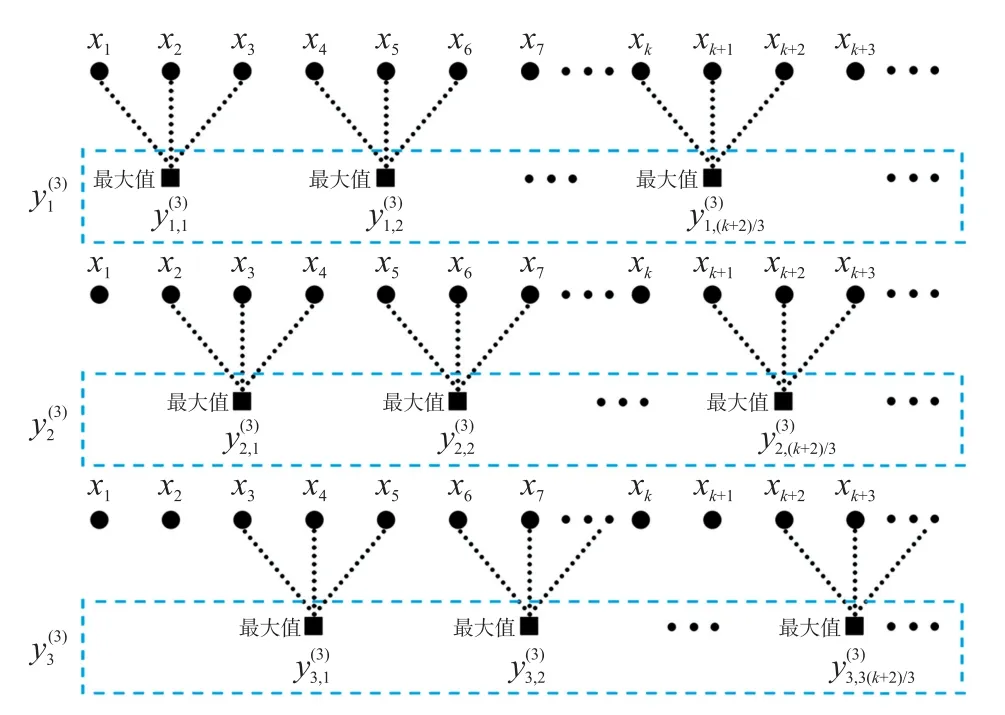
图2 尺度因子τ=3 时的IRCMNDE 粗粒化过程
式中:abs 为绝对值函数。然后计算粗粒化时间序列熵值,并进行归一化,得到IRCMNDE,如式(11)所示:
1.3 概率神经网络
概率神经网络(PNN)算法是一种监督型机器学习模式识别算法。其原理主要基于贝叶斯最小风险决策理论和人工神经网络模型,能实现任意的非线性逼近,并收敛到贝叶斯分类的最优解,利用Parzen 窗口估计方法计算样本总体分布的概率密度,以达到模式分类的目的。
具体的学习步骤如下:
①将归一化后的样本数据输入概率神经网络的模态层,假设样本个数为p,每个样本的特征向量维数为m,则输入样本矩阵大小为p×m,计算归一化后的样本数据与训练样本数据之间的欧氏距离,如式(12)所示:
②选择径向基函数(RBF)作为激活函数,对输入的样本数据和待识别的样本数据进行处理,如式(13)所示,得到初始概率矩阵P:
③根据式(13)计算模式层的输出值,然后计算待识别样本是属于未变性组织还是变性组织的初始概率和,如式(14)所示,最终实现组织变性识别:
2 实验分析
2.1 实验系统
HIFU 辐照实验系统如图3 所示。在辐照实验之前,在水箱中加入聚维酮去除水中的气泡,以防影响实验结果。采用中心频率为1.39 MHz 的HIFU换能器辐照固定在橡胶板上的新鲜离体猪肌肉组织(组织厚度为40 mm),辐照功率为210 W~300 W,辐照周期为0.1 ms~0.2ms。通过PC 机操作HIFU控制系统调整HIFU 换能器的辐照位置。采用光纤水听器(FOPH2000,德国)采集HIFU 回波信号,通过示波器(MDO3032,美国)保存到PC 机端。在本文中,从15 例猪肌肉组织中总共获取124 个HIFU回波信号(包括62 个未变性状态与62 个变性状态)。此外,HIFU 辐照靶区位置的温度计被用于测量辐照区域的温度,并通过组织切片获取生物组织变性状态。图4 为未变性组织与变性组织切片图。
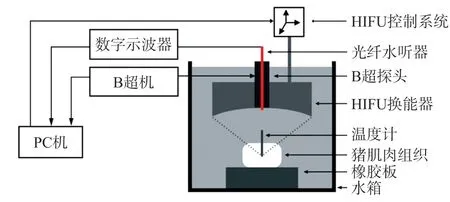
图3 HIFU 辐照实验系统
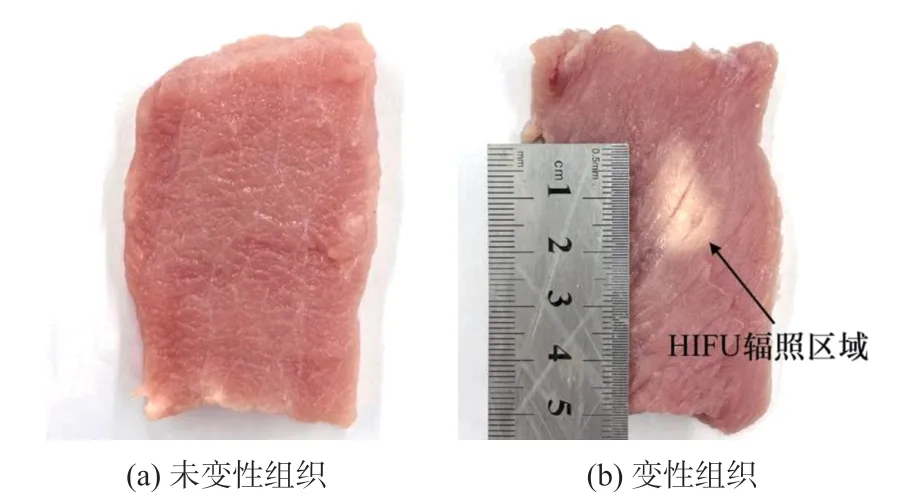
图4 未变性组织与变性组织切片图
2.2 模拟信号分析
为了证明所提IRCMNDE 方法的优越性,根据相关文献[17-18],将30 组数据长度为3 000 的1/f噪声作为模拟信号用于分析MDE、RCMDE 以及IRCMNDE 在不同参数下的熵值分布。我们选择嵌入维度参数m=2、3,类别数量c=3、6、9,延迟时间d=1。图5 所示为尺度因子1-20 的1/f噪声不同参数下的熵值均值标准差图(每个数据点为该尺度下的熵值均值,竖直方向标记长度为熵值标准差)。从图5 可以明显看出,随着尺度因子的增大,1/f噪声的MDE 和RCMDE 值的下降趋势尚不明显,表明MDE 和RCMDE 对1/f噪声的多尺度分析优势不能得到有效的展现,出现了信息丢失的问题。而1/f噪声的IRCMNDE 值随着尺度因子的增大均呈现一个明显的下降趋势,且下降速度比MDE 和RCMDE更快,这意味着IRCMNDE 有效克服了粗粒化过程导致的信息丢失问题,能有效提取1/f噪声的熵值特征。此外,随着嵌入维度m和类别数量c的增大,MDE 和RCMDE 值受m和c 参数变化的影响较大,IRCMNDE 值受m和c参数变化的影响较小,这意味着对熵值的归一化处理能减弱不同参数选择导致的熵值波动。
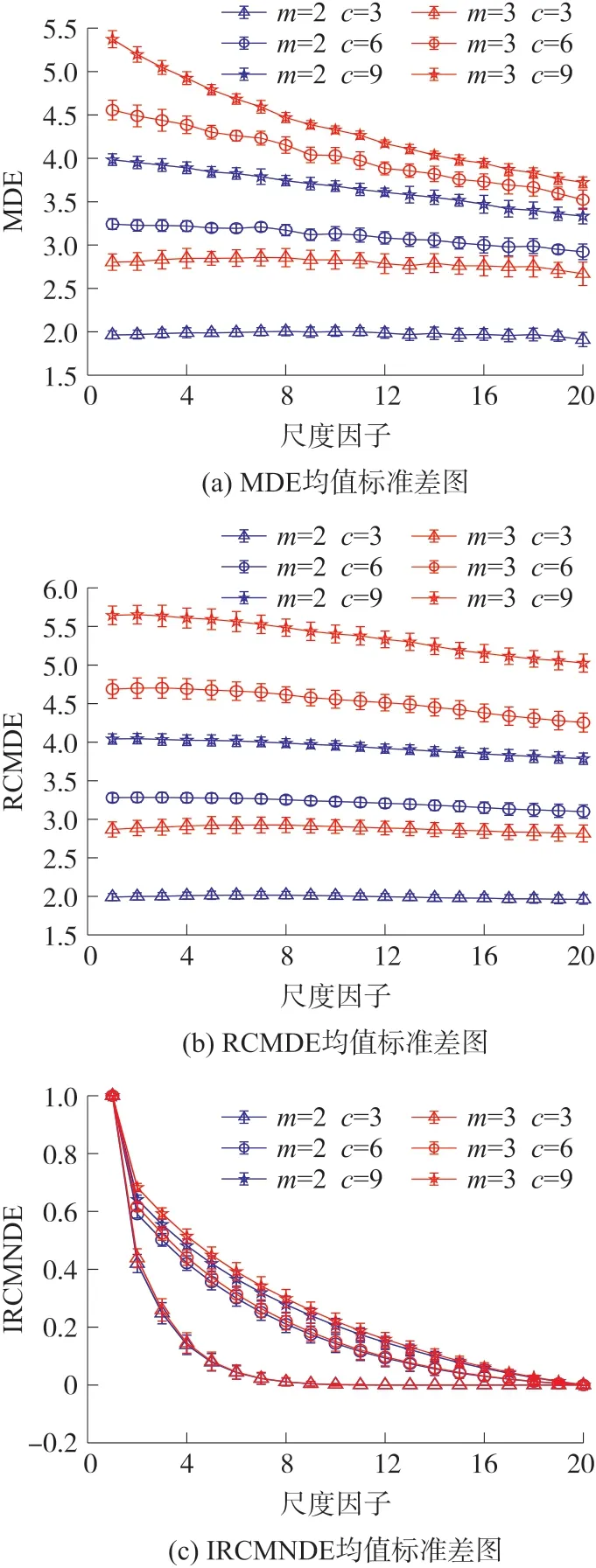
图5 不同参数下的1/f 噪声MDE、RCMDE和IRCMNDE 均值标准差图
2.3 HIFU 回波信号分析
图6 所示分别为未变性组织与变性组织的HIFU 回波信号时域图。选择嵌入维度m=3,类别数量c=3,延迟时间d=1,分别提取124 个HIFU 回波信号(包括62 未变性状态与62 变性状态)的MDE、RCMDE 以及IRCMNDE 熵值特征,如图7 所示。可以发现,MDE、RCMDE 以及IRCMNDE 熵值随着尺度因子的增加均呈现下降的趋势;未变性组织与变性组织HIFU 回波信号的MDE 熵值曲线在所有尺度下均存在大量重叠,难以精确区分未变性组织与变性组织。RCMDE 熵值曲线与MDE 基本一致,相较于MDE,RCMDE 的标准差更小,但仍然存在大量重叠部分,给生物组织变性识别带来很大难度。而IRCMNDE 在尺度因子为2、3、4、5 时,通过熵值曲线能清晰地区分未变性组织与变性组织,均值标准差曲线没有重叠。这是因为MDE 与RCMDE 在粗粒化过程中采用平均值计算,容易中和HIFU 回波信号突变信息,出现了信息丢失。而IRCMNDE 在粗粒化过程中采用最大值计算,利用最大值计算得到的新粗粒化序列近似于原始信号的包络线,保证了HIFU 回波信号信息的正确性,避免了信息丢失的不足,能较好地突出生物组织变性特征,为后续生物组织变性识别提供区分度更高的特征参数。此外,HIFU 回波信号IRCMNDE 的标准差明显小于MDE、RCMDE,这意味着相较于MDE 与RCMDE,本文所提IRCMNDE 方法在分析HIFU 回波信号时具有更高的鲁棒性。

图7 HIFU 回波信号的MDE、RCMDE 以及IRCMNDE 均值标准差图
另外,为验证归一化处理可减弱不同参数选择导致的HIFU 回波信号熵值波动,分别计算m=3,c=3,d=1 和m=2,c=3,d=1 参数下MDE、RCMDE以及IRCMNDE 的熵值差,结果如图8 所示。纵坐标为不同参数下的熵值差,可以看出相较于MDE 和RCMDE,IRCMNDE 的熵值差较小,熵值更稳定,说明熵值归一化处理可减弱不同参数选择导致的熵值波动,IRCMNDE 能更有效地提取HIFU 治疗过程中生物组织的变性特征。

图8 不同参数下MDE、RCMDE 以及IRCMNDE 的熵值差
2.4 变性识别
利用概率神经网络(PNN)分别对提取的HIFU回波信号MDE、RCMDE 和IRCMNDE 特征进行分类识别。随机选择62 个HIFU 回波信号(包括31 个未变性状态与31 个变性状态)作为训练集,其余62 个HIFU 回波信号作为测试集,PNN 平滑因子参数设定为1.5,图9 所示为MDE-PNN、RCMDE-PNN 和IRCMNDE-PNN 的变性识别效果图。横坐标为HIFU 回波信号样本编号,纵坐标1 代表未变性组织状态,纵坐标2 代表变性组织状态,可发现MDE-PNN 有6 个误识别样本,RCMDE-PNN 有5 个误识别样本,IRCMNDE-PNN 的误识别样本只有2 个,低于MDE-PNN和RCMDE-PNN。另外将本文方法与文献[11]中MPE 方法进行比较,分别计算MPE-PNN、MDE-PNN、RCMDE-PNN 和IRCMNDE-PNN 的变性识别率和运行时间,结果如表1 所示。相较于MPE-PNN、MDEPNN 以及RCMDE-PNN,IRCMNDE-PNN 方法能正确识别更多的未变性组织与变性组织样本,基于IRCMNDE 的变性识别方法识别率最高,达到96.77%。上述结果再次验证了IRCMNDE 方法在表征生物组织HIFU 回波信号变性特征上的有效性和优势。
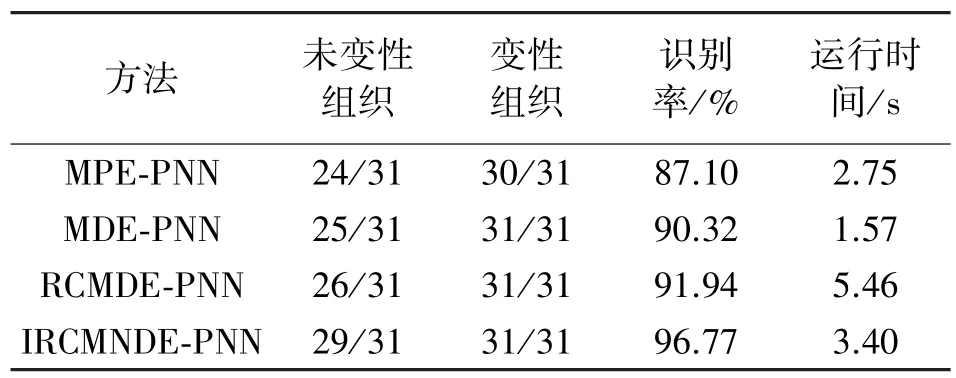
表1 特征参数对识别效果的影响

图9 基于不同特征参数的PNN 变性识别效果图
此外,对比不同算法的运行时间,发现MDE 方法运行时间低于MPE,IRCMNDE 和RCMDE 运行时间多于MDE 方法,这是因为精细复合多尺度熵在提高熵值稳定性的同时,降低了运算效率。而IRCMNDE 运行时间低于RCMDE 是因粗粒化过程中的平均值计算被替换为最大值计算,这在一定程度上减少了算法的计算量。
3 结论
本文针对传统多尺度散布熵(MDE)方法的缺点,提出了一种改进精细复合多尺度归一化散布熵(IRCMNDE)作为生物组织HIFU 回波信号的变性特征。模拟实验结果表明,相较于MDE 和RCMDE,IRCMNDE 方法在分析信号复杂度时有效克服了粗粒化过程导致信息丢失的不足,避免了熵值不稳定的问题。此外,IRCMNDE 中的归一化处理可减弱不同参数选择导致的熵值波动。将所提方法应用于实际HIFU 回波信号,结果表明,相较于多尺度排列熵(MPE)、MDE 以及RCMDE,IRCMNDE 能更稳定地表征生物组织HIFU 回波信号的变性特征,通过PNN 进行变性识别,基于IRCMNDE 特征的误识别样本更少,变性识别率更高,达到96.77%。综上,基于IRCMNDE 的生物组织变性识别方法能更好地识别HIFU 治疗过程中生物组织是否发生变性,对指导医生进行准确的HIFU 疗效评价提供技术支持,具有一定的理论意义和临床实用价值。虽然本文所提生物组织变性识别新方法正确高效,但IRCMNDE方法还未在其他领域证明其有效性,尚需进一步研究与实践检验。
