机械陀螺仪式双足机器人机械设计及优化分析*

吴海青，何满塘，张小强

（太原工业学院机械工程系，太原 030008）

0 引言

随着移动机器人应用场景从单一、结构化的环境逐渐拓展到复杂、非结构化的环境，传统的足式和轮式移动机器人难以胜任复杂环境和复杂任务的需求[1]。轮腿式机器人兼顾了轮式机器人在平整路面上的快速平稳移动和腿式机器人在崎岖路面上的高越障性等特点[2]，是一种自适应能力强，适合于在复杂环境中作业的机器人，在许多未知危险的场合中可以协助甚至代替人类完成作业[3]，具有广泛的应用前景。为提高机器人的地形适应性，并吸取轮式与足式机器人的优点，国内外相关学者开展了特殊结构移动机器人关键技术方面的研究[4]。而双足轮腿式机器人拥有机动性高、场地适应性强、能耗低以及运动噪声小等优点，更受到了各行各业的青睐。国外典型的双足轮腿混合结构式机器人主要有美国波士顿公司研制的Handle机器人[5-7]和苏黎世联邦理工学院研制的Ascento 机器人[8-9]等。国内典型代表有：2019 年哈尔滨工业大学深圳校区研制的SR600 轮腿机器人[10]；2020 年南方科技大学HuaChen 等[11]研制的能实现跳跃的机器人NeZha；2021 年腾讯AILab 及RoboticsX 实验室研制的Ollie 机器人，哈尔滨工业大学机器人技术与系统国家重点实验室研制的机器人WLR，本末科技研制的刑天-Diablo 机器人，以及在Robomaster 比赛中，部分参赛队伍设计的平衡步兵等。

本文提出一种新型轮腿混合式双足机器人构型，通过加装机械陀螺仪可实现机器人的平衡以及抬腿动作，具有占用空间小、灵活性强以及可在复杂路况下行走等优点，能够应用于物流运输、外卖快递、军用地面探测以及医疗等领域。

1 轮腿式双足机器人总体方案设计

1.1 三维结构模型

所研究的轮腿式双足机器人三维模型如图1 所示。该机器人由身体、腿部结构以及控制系统等组成，腿部采用“鹤式”四杆机构，每条腿部机构由大腿、小腿、连杆、脚轮4 个部分组成，腿部舵机通过齿轮传动带动大腿运动，从而驱动整个腿部机构运动，足端电机驱动轮子转动。在身体最上面放置机器人的控制系统，在主控固定板上安装STM32 单片机、超声波模块、蓝牙模块、机械陀螺仪模块等部件。在身体之间的固定板上安装机械陀螺仪、电池、驱动器等部件。

图1 轮腿式双足机器人三维模型

所设计的机器人可实现在自身高度变化平衡后，身体保持在前后方向角度不变；控制2 个轮腿各自伸缩，可实现身体左右倾斜角度自由改变；利用机械陀螺仪的进动原理，可实现机器人的抬腿动作；在满足强度与刚度前提下，对大腿及大腿齿轮、小腿和身体机架进行轻量化设计，实现机器人整体质量的减轻。

1.2 腿部机构选型与尺寸设计

根据人体仿生学可知，人类腿部关节角度变化与连杆机构相似，而能实现端点近似直线运动的四连杆机构有曲柄滑块机构、2-4-5 连杆直线机构、鹤式起重机连杆机构等，从便于加工与设计方面考虑，鹤式起重机连杆机构更加符合人类的腿部结构。

通过计算机辅助图解法进行四连杆机构各杆件长度的设计，四连杆机构各杆件长度的优化是提高四连杆端点运动轨迹线性度的关键[12]。

采用Creo7.0辅助建模绘制出腿部机构极限位置的运动轨迹简图，如图2 所示。设轮轴与大腿转动轴在同一竖直方向上，为保证轮子电机有足够的运动空间，设身体在最矮时，轮子与地面的接触点到大腿转动轴轴线距离为60 mm，此时为确保拥有150 mm 的伸缩量，身体在最高处时，轮子与地面的接触点到大腿转动轴轴线的距离为210 mm。此时，设大小腿长相等且采用连杆与小腿共线。为确保腿的传力性能，设身体在最高和最矮时的传动角均为50°，控制对应杆长度相同。根据模拟发现，机构出现弱尺寸时，则推断轮子在运动过程中会与竖直轴线有a、b、c、d共4 个交点，将直线ac分成3 段，再次绘制出中间位置点（点d）的腿部机构运动轨迹简图如图3所示，并得到大腿的预期尺寸在132.69 mm左右。

图2 极限位置运动轨迹图解分析

图3 中间位置运动轨迹图解分析

令大腿长度为130 mm，并将直线ac等分3 段，设从动杆尺寸为40 mm，再次绘制腿部机构运动轨迹简图，得出腿部机构各构件的尺寸如图4 所示。绘制一个位置的简图进行尺寸阵列，如图5 所示，得出轮足端的运动轨迹近似为一条直线，进而确保机器人重心在轮轴线上方，实现机器人在自身高度变化平衡后，其身体保持在前后方向角度不变。

图4 腿部机构各构件尺寸

图5 某位置运动轨迹简图尺寸阵列

采用上述参数，解得身体在最矮和最高时，传动角γmin1=47.85°＞40°（符合许用传动角），γmin2=53.07°＞40°（符合许用传动角），故该设计合理。

根据所得数据，采用Creo7.0自顶向下设计，绘制出腿部机构的初始模型如图6所示。

图6 腿部机构建模

1.3 腿部减速机构设计

在电机选型过程中，选择转矩为2 N·m 的ZP20S 舵机为动力驱动腿部机构。考虑到大腿输入扭矩的需求，按1/4 减速比进行腿部减速机构设计。舵机齿轮采用标准化齿轮设计，齿数z1=17，模数m=1.5 mm。通过Creo7.0 测得舵机齿轮的齿根圆直径为21.75 mm，可与舵盘直接配合连接。

大小齿轮啮合如图7 所示。大腿齿轮采用不完全齿轮设计，其有效啮合角度为45°，两侧采用圆弧限位。齿轮重合度计算公式为：

图7 大小齿轮啮合

式中：z1为舵机齿轮齿数，取17；z2为大腿齿轮齿数，取68；α1为舵机齿轮齿顶圆压力角，取35.75°；α2为大腿齿轮齿顶圆压力角，取23.45°；α′为分度圆压力角，取20°。

将数据代入式（1）中，解得重合度ε≈1.72 ＜2，则两个齿轮在分度圆处啮合时只有一对齿接触，此时单对齿接触受力F满足：

式中：d1为舵机齿轮分度圆直径，取25.5 mm；T为舵机扭矩，取2 N·m。

1.4 优化设计

1.4.1 大腿齿轮优化

通过Creo7.0 对大腿齿轮的初始模型添加材料与载荷，材料选择FR4 玻纤板，最小屈服极限为298 MPa，玻纤材料密度为1.9 g/cm3，通过软件计算可得，大腿齿轮的初始模型质量约为16.98 g。

利用Creo7.0对大腿齿轮的初始模型进行应力应变求解，由于两对齿轮组的重合度小于2，故可以简化为对每个齿分别进行分析，即多工况分析，取每个工况载荷F=200 N，方向垂直齿面，固定约束一致。对比11 个载荷工况的分析结果，当载荷作用在第一个齿面上时，应力和应变均最大，最大形变为0.032 8 mm，应力值最大为77.49 MPa，小于屈服应力298 MPa，第一个齿面的应力和应变分析结果如图8所示。

图8 第一个齿面的应力应变分析结果

然后对初始模型进行创成式轻量化设计，采用刚度最大化设计，保留46.5%的材料，优化后大腿齿轮模型如图9 所示。然后进行几何重建，如图10 所示。分辨率选择高级分辨率，通过软件可以算出优化后大腿齿轮模型质量约为7.6 g。

图9 优化后大腿齿轮模型

图10 几何重建

通过ANSYS Workbench对重建模型进行应力应变验证分析，对比11个载荷工况的分析结果，当载荷作用在第一个齿面上时，应力和应变均最大，最大形变为0.040 mm，应力最大为83.12 MPa，小于屈服应力298 MPa，优化后第一个齿面的应力和应变分析结果如图11所示。

图11 优化后第一个齿面的应力应变分析结果

通过创成式轻量化设计，在保证强度和刚度的前提下，大腿齿轮模型的质量减少了53.5%。

1.4.2 大小腿与身体结构优化

采用Creo 创成式优化设计技术，对小腿、大腿与身体进行轻量化设计。以刚度最大化为设计目标，保留40%的材料进行优化，优化后再利用ANSYS 对强度和刚度进行验证分析。小腿、大腿与身体优化前后对比如图12 所示，在保证强度和刚度的前提下，小腿、大腿和身体的质量均减轻了60%，而且均采用增材制造技术进行加工，具有结构刚度大、质量轻、外形美观等优点。

图12 优化前后对比

1.5 机械陀螺仪结构设计

1.5.1 机械陀螺仪工作原理

陀螺仪进动如图13 所示。由角动量定理可得，高速旋转的陀螺仪一端架在支点上可以实现陀螺绕支点旋转而不会掉下来，这个过程称之为“进动”过程[13]。

图13 陀螺仪进动示意

机械陀螺仪在高速旋转时可以通过一个支点“悬空”，利用这个原理可以使轮足机器人实现抬腿动作。同时当机器人在走直线路径时，机械陀螺仪可以更好地限制自身做转动运动，从而保证身体稳定，利用这一点可以给机器人装载一些运动执行机构，如机械臂、无人作战器械等，以提高执行机构运动的稳定性与可靠性。

此外，机械陀螺仪的另一个作用是当陀螺仪惯性飞轮在低速旋转时，可以产生一个惯性扭矩，当机器人产生一定倾角时，惯性飞轮会加速转动产生与倾倒方向相反的力矩，该力矩会抵消机器人受重力或扰动影响而产生的力矩，从而将机器人“扶正”，使其能够快速回到平衡位置[14-16]。

1.5.2 机械陀螺仪设计

机械陀螺仪三维模型如图14 所示。将惯性飞轮设计在电机正中间，尽可能使得其体积小、质量轻、惯量大，且回转重心靠近几何中心。惯性飞轮采用45 钢金属材质，利用联轴器将其塑料固定座固定到电机轴上。电机固定座采用夹持方式固定在装有电池的重心调节板上，使得电机可以轴向窜动，进而能更好地调节机械陀螺仪的重心位置，使其尽可能在几何中心。

图14 机械陀螺仪三维模型

将机械陀螺仪与电池固定在一起，作为机器人的配重模块，通过重心调节板水平方向的微调整，进而控制机器人重心的位置尽可能控制在轮子中心的上方。

1.5.3 带有机械陀螺仪的足式机构动力学仿真

综上所述，通过分析乘法分配律与小数乘法的关联性，找到学习小数乘法意义的新方法：运用已经习得的乘法分配律的相关知识内容将小数乘法的表达式变形，以此理解小数乘法的多重含义.这样的教学思路不仅能够加深学生对于小数乘法意义的多种理解，同时也巩固了与运算律相关的知识内容，对乘法分配律的应用也更为灵活.因此，在教学中教师应注意对小数乘法意义的全面讲解，打破对其含义理解的单一模型，让学生学会运用已有知识经验解决新问题.

利用ADAMS 软件对机械陀螺仪基础模型进行建模，如图15所示。惯性轮通过转动轴连接于转轴上，转轴与底座通过球副连接，底座与大地连接。设置重力方向为y轴负向，设置旋转驱动到转轴与惯性轮的转动轴上，角动量方向为转轴轴向远离支点侧，函数为36 000 d（36 000°/s）。

图15 机械陀螺仪基础模型

运行仿真后，得到陀螺仪在俯视方向作逆时针旋转运动。以转轴质心为研究对象进行测量，原点坐标系为底座中心，采用笛卡尔形式显示质心xyz轴坐标的位置，如图16所示。由图可知，机械陀螺仪在水平方向做逆时针旋转运动，机械陀螺仪在重力（y）方向的位置保持在33～40 mm浮动，前1.5 s过程中，由于惯性轮带动转轴旋转，转轴加速提高了整体角动量，转轴质心会在y方向产生一定的波动，但在随后的时间里，由于转轴速度逐渐平稳，陀螺仪也保持在35 mm高度稳定下来，这个仿真结果与实际相符。

图16 转轴质心xyz轴坐标位置

设想机械陀螺仪可替换支点如图17 所示，惯性轮转动方向不变，当支撑端在左侧时，陀螺仪角动量L沿着转轴轴线背离转轴支点，重力与支点支撑力产生的力偶M垂直支撑杆轴线与转轴轴线平面指向里侧，此时由角动量定理，陀螺仪将在俯视方向做逆时针转动。同理，当机械支点切换至右侧时，此时陀螺仪角动量L沿着转轴轴线指向转轴支点，重力与支点支撑力产生的力偶M垂直支撑杆轴线与转轴轴线平面指向外侧，此时由角动量定理，陀螺仪将在俯视方向做顺时针转动。

图17 机械陀螺仪支点替换

通过这个原理，可以对一个简单行走机构进行模拟。首先对行走机构进行建模，如图18 所示。惯性轮通过转动轴连接于转轴上，转轴与左右的支撑柱通过球副连接，支撑柱与脚座通过滑块连接。

图18 简单行走机构模型

设置脚座与大地接触力，重力方向为y轴负向；设置旋转驱动到转轴与惯性轮的转动轴上，函数为36 000 d（36 000°/s）；设置直线驱动分别到左右脚座与左右支撑柱，左腿、右腿的驱动函数如下。

到左腿的函数为：

到右腿的函数为：

左、右腿直线驱动的作用效果为左右脚座依次升降，同时保证每时每刻左右支点的最高位置不变。

图19 简单行走机构转轴质心xyz轴坐标位置

2 轮腿式平衡机器人控制系统

轮腿式平衡机器人的控制系统可实现对机器人姿态、速度、方向等的监测，通过控制算法处理传感器信号后，控制执行机构如双轮足电机、机械陀螺仪电机、控制腿部伸缩的舵机等完成相应动作，从而实现机器人的行驶运动控制以及自主平衡控制。硬件系统结构如图20所示。

图20 硬件系统结构示意

机器人在行驶过程中会受到很多外界因素干扰，因此机器人的平衡控制系统需要具有良好的抗干扰能力。控制系统能否迅速高效地对机器人的平衡做出反应起到至关重要的作用，因此控制系统对主控芯片的性能要求较高，并且由于机器人的驱动模块较多，主控芯片需要具有较多的接口。根据以上要求，采用STM32 系列芯片，其中STM32F103C8T6 型号芯片拥有37 个I/O 接口、4 个16 bit 的定时器、64 KB 程序存储容量以及20 KB 的RAM 容量，且工作电压约为3 V，系统时钟最高能采用72 MHz 的频率，拥有成本低、性能高、功耗低等优点，满足所需要求。

控制腿部伸缩舵机即姿态关节调节电机，要求能够确定腿部机构位置且拥有足够大的扭矩。经过计算可知大腿输入转矩要大于6.4 N·m，ZP20S舵机扭矩为2 N·m、转角范围为180°，对其加4倍减速比，转角缩至45°，且转矩可增至8 N·m，大于6.4 N·m，安全系数达1.25，满足需求。

两个轮子的驱动电机要求能够进行速度检测，故采用编码电机，驱动器采用一个TB6612FNG 驱动模块即可驱动两个电机。

检测机器人姿态的传感器选用MPU6050 陀螺仪模块，当检测到机器人姿态为非平衡姿态时，机械陀螺仪充当动量轮，利用惯性飞轮低速旋转产生惯性扭矩，从而实现平衡控制。机械陀螺仪电机需要能够满足速度检测、转速较高的要求，故采用无减速器的编码电机作为驱动电机，采用L298驱动器驱动。

HC05蓝牙模块可实现上位机与机器人交互通信，实现对机器人运行状态监控，并以反馈控制的方式提高机器人的控制精度。

采用3节18650电池为机器人各个电机模块提供能源的电源模块供电；另外，还需要稳压模块以及开关导线若干。

3 优化后整机建模分析

对优化后的零件进行组装，并添加零件的材料属性，确定总装配体重心位置，通过调整配重改变重心位置，使得身体水平时重心落在轮子与地面接触点的正上方。

通过测量得到机器人蹲下时高度为190 mm，站立时高度为360 mm，从而可知机器人高度变化为170 mm，大于期望的150 mm 的高度变化目标。质量测量如图21所示。通过质量测量，测得机器人总质量约为2.215 kg，实现了整机轻量化设计。重心测量如图22所示，通过测量机器人不同姿态下的重心位置，发现重心始终在轮轴线正上方，满足腿部结构设计要求。

图21 质量测量

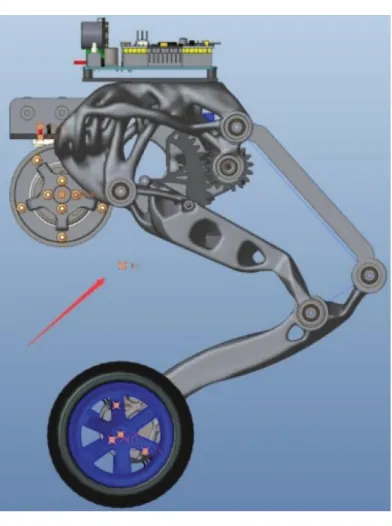
图22 重心测量

4 结束语

本文利用高速旋转的陀螺仪可通过一个支点“悬空”的原理，实现了轮腿式双足机器人的抬腿行走动作。此外，当姿态传感器MPU6050 检测到机器人姿态为非平衡状态时，陀螺仪的惯性飞轮会加速旋转产生与倾倒方向相反的力矩，从而使机器人快速回到平衡位置。为了验证上述理论，利用ADAMS软件对一个装了陀螺仪的简单行走机构进行了动力学仿真，设置直线驱动分别在左右脚座与左右支撑柱上。结果表明：陀螺仪在重力y方向上可在35 mm高度处保持稳定，验证了加装机械陀螺仪的双轮足机器人能够实现抬腿行走的动作，并保持平稳的状态。

通过轻量化设计，机器人的整体质量降低了55.7%，大大降低了制作的材料成本，同时保证了机器人的运动特性。采用Creo7.0创成式优化设计技术，大大缩短了开发周期。与传统的拓扑优化相比，该技术分析方便简单、求解速度快、模型修改方便，优化后达到了刚度更大、强度更高且外形更加美观的目的。