基于响应面模型涡轮叶片冷却性能的数值研究

2024-01-09高建民李云龙

燃气轮机技术 2023年4期

赵振,席雷,高建民,徐亮,李云龙

(西安交通大学机械制造系统工程国家重点实验室,西安 710049)

燃气轮机被广泛地应用于发电、机械驱动等能源和国防领域,代表着国家安全和整体经济发展的高端核心技术动力装备[1]。而国外严格阻碍着我国燃气轮机的发展,尤其是先进的燃气轮机高温涡轮叶片冷却技术,我国叶片的冷却技术面临着涡轮叶片冷却机理匮乏、基础数据缺失等难题。使用实验手段和数值模拟结合的方式对涡轮叶片冷却性能的研究对突破我国燃气轮机高温涡轮叶片的发展和自主设计尤为重要。

目前随着计算流体力学和计算机技术的发展,耦合传热数值分析方法已经能够满足大部分的传热研究。叶片实验面临着成本昂贵、测量精度难以保证等困难,因此,使用数值方法对叶片实验进行补充和冷却机理的探究将是未来涡轮叶片冷却技术发展的有效途径之一。许多国内外专家学者针对叶片的冷却性能开展了数值研究。罗磊等[2]为了降低叶片的表面温度和提高叶片的气动效率,采用气热耦合数值方法对叶片的叶型和冷却结构进行了优化。胡捷等[3]采用非耦合和气热耦合传热方法对Mark Ⅱ 叶片进行了数值研究,结果表明非耦合方法与气热耦合方法相比存在较大的计算偏差,采用气热耦合传热方法对叶片进行数值研究具有更高的准确性。董平等[4]采用气热耦合传热方法对Mark II叶片进行了数值模拟,研究表明叶片表面的流动比较复杂,使用转捩模型得到的数值结果与实验结果吻合得较好。Luo等[5]采用耦合传热方法对三种工况下NASA涡轮叶片的流动和传热特性进行了预测,结果表明耦合传热方法可以成为涡轮叶片传热分析和冷却结构设计的可行工具。John等[6]研究表明耦合传热分析的计算结果比非耦合传热的计算结果更加准确,这是因为耦合传热充分考虑了固体表面温度分布对流体热边界层的影响。Nowak等[7]的研究结果表明耦合传热数值方法对叶片温度场的预测效果很好。Zhu等[8]采用耦合传热方法分析了多种湍流模型具有热障涂层涡轮叶片表面的温度和流场分布,结果表明通过耦合传热数值方法获得的计算结果和实验结果较吻合。

现有的研究基本都是采用单因素分析法,即研究单参数发生变化对叶片冷却性能的影响,且主要研究的参数有叶片的入口雷诺数、冷气与主流温度比及流量比等无量纲参数。本文为了精细化研究,将叶片冷却系统看成一个复杂系统,通过改变主流入口温度、主流出口压力、主流进出口压比、冷气与主流温度比及流量比等参数可以精准的调节叶片冷却系统。因此,研究了上述参数对叶片冷却性能的影响,并对上述设计参数进行了试验设计。现有表征叶片冷却性能的经验公式一般采用幂函数形式拟合,其拟合精度相对较低,需要探究新的经验公式拟合。此外,现有研究在探究叶片的冷却性能时,采用的评价指标大多仅有冷却效率,而叶片冷却的主要目的是得到均匀且较低温度分布的叶片,对叶片的无量纲温度分布的研究也是十分有必要的。因此,本文基于试验设计和响应面模型相结合的方式,采用流-固耦合传热方法对某型高温涡轮叶片的无量纲温度分布进行了数值研究,对涡轮叶片的工况参数进行了试验设计,探究了主流入口温度、主流出口压力、主流进出口压比、冷气与主流温度比及流量比对涡轮叶片无量纲温度分布的影响规律,并采用响应面模型拟合得到有关涡轮叶片平均无量纲温度的经验公式。

1 研究对象

1.1 数值模型

采用商用软件CFX对某型涡轮叶片通道的冷却性能进行流-固耦合传热数值研究,研究过程中将数值研究的残差水平包括连续性方程、动量方程及能量方程等均设置为10-6。图1给出了某型涡轮叶片通道的数值模型。由图1可知,为了研究方便,仅提取了一个叶栅流道进行研究,因此将涡轮叶片的左、右流道设置为周期性边界条件。主流的入口设置为与实验相同的总温和总压边界条件,出口设置为平均静压。冷气入口设置为静温和静压边界条件,出口设置为质量流量。涡轮叶片与冷气和主流接触的壁面设置为流-固交界面,具有相同的热流密度分布和温度分布,其余的叶片壁面设置为绝热壁面。此外,为了保持与实验的一致性,在冷气通道的入口和出口分别添加了100 mm的稳流段。另外,由图1可知,本文研究的涡轮叶片具有五个直通的内冷通道,其叶型为某F级燃气轮机第一级静叶的中截面拉伸而成的直叶片,材质为304不锈钢。

图1 数值模型

1.2 数值验证

图2为涡轮叶片通道主流流体域的网格模型,流体域网格均采用ICEM软件进行结构化网格划分。其余网格均较简单,所以未给出。对近壁面的网格进行细分处理,第一层网格尺寸为0.001 mm,网格膨胀比为1.2。这样的设置可以保证网格的y+值小于等于1。本课题组前期对涡轮叶片冷却性能的数值研究表明SSTk-ω湍流可以有效地得到其流动与传热性能[9-10],因此本文也选择SSTk-ω湍流模型。

图2 网格模型

图3给出了涡轮叶片通道的网格无关性验证。其中,纵坐标ηave为涡轮叶片的平均无量纲温度,横坐标为网格数量。由图可知,共划分了总网格数分别为122万、183万、233万、290万、360万等5套网格。当网格数增大时,涡轮叶片的平均无量纲温度也会增大,而当总网格数增大到290万时,叶片的平均无量纲温度不再随网格数的增大而增大,即达到了网格无关性的要求。

图3 网格无关性验证

图4分别给出了涡轮叶片表面的无量纲温度的实验测量值和数值计算值。图中,纵坐标η为涡轮叶片表面无量纲温度。横坐标S/Smax为叶片的相对轴向弦长,S/Smax<0表示叶片的压力面,S/Smax>0表示叶片的吸力面。图4所示的实验工况为:主流入口温度为695 K,主流出口压力为140 kPa,主流进出口压比为1.4,冷气与主流温度比为0.65,流量比乘以100为5.5。由图4可知,实验测量和数值计算得到的涡轮叶片表面的无量纲温度分布曲线的趋势基本相同,最大偏差为4.8%。这说明SSTk-ω湍流模型和耦合传热可以较为准确地获取涡轮叶片表面的无量纲温度分布。

图4 数值验证

1.3 数据处理

SSTk-ω模型是由Menter等在k-ω模型的基础上提出的[11],它在近壁面使用k-ω模型,而在近壁面边界层周围及自由剪切层采用k-ε模型,这样可以提高预测流动分离现象的准确性。SSTk-ω模型的流动方程如下:

(1)

(2)

涡轮叶片表面的无量纲温度公式如下:

(3)

式中:Tw为涡轮叶片表面的当地温度。

涡轮叶片的平均无量纲温度公式如下:

(4)

式中:A为涡轮叶片表面面积。

1.4 响应面模型

响应面模型可以通过对设计参数进行试验设计,得到设计参数范围内设计变量与响应面之间的经验关联式,响应面模型的公式如下[12]:

Y=f(X)+ε=Xα+ε

(5)

式中:Y为响应;X为设计变量;f(X)为目标的近似函数;α为拟合系数;ε为预测误差。

近似函数f(x)选取常用的具有较高准确性的二阶多项式响应面模型,公式如下:

(6)

式中:系数α=[α0,…,αk,α11,…,αkk,α12,…,α(k-1)k]T;xi和xj是设计变量;k为设计变量的个数。

表1给出了叶片工况参数的设计表,采用中心符合设计对叶片工况参数进行试验设计。由表1可知,设计表主要包括序号、设计参数和响应,去除重复的设计点后共有43个样本点。设计参数中Tgi为主流入口温度、pgo为主流出口压力、pr为进出口压比、Tr为冷气与主流温度比、Mr为冷气与主流流量比乘以100,分布范围分别为680～710 K、120～140 kPa、1.3～1.5、0.6～0.7、5～8。

表1 工况参数设计表

2 结果分析与讨论

图5给出了当所有设计参数均处于中值时叶片表面的无量纲温度分布,而当研究其余设计参数的影响时,图5均作为中间图进行对比分析。图中,横坐标-1～1表示涡轮叶片的无量纲相对轴向弦长,-1～0表示叶片的压力面,0～1表示叶片的吸力面。由图5可知,当设计参数均为中值时涡轮叶片表面无量纲温度的分布处于0.79～0.94。其中,涡轮叶片叶根位置的无量纲温度要高于叶片的叶尖位置,这是因为冷气是从叶片的叶尖流入,从叶片的叶根流出,冷气对叶片叶尖位置的冷却要优于叶片的叶根位置。总体而言,涡轮叶片压力面的无量纲温度比吸力面低约1.5%。叶片叶尖中弦区的区域有最低的无量纲温度分布,其数值处于0.8左右。叶片尾缘叶根的位置存在最差的冷却效果,其无量纲温度可达最高的0.95左右。涡轮叶片前缘直接受到来流的高温冲击,因此有较差的冷却效果,其无量纲温度为0.91左右。此外,主流入口温度对叶片表面无量纲温度的分布基本不产生影响。

图5 设计参数均为中值时涡轮叶片无量纲温度分布

2.1 主流出口压力的影响

图6给出了主流出口压力对涡轮叶片表面无量纲温度分布的影响。由图6(a)和6(b)可知,当主流出口压力发生变化时,叶片表面无量纲温度的分布处于0.79～0.94。涡轮叶片叶根位置的无量纲温度要高于叶片的叶尖位置,叶片压力面的无量纲温度要低于吸力面,无量纲温度最低的区域处于叶片叶尖中弦区的位置,叶片尾缘叶根的位置存在最差的冷却效果,叶片前缘有较高的无量纲温度。当主流出口压力增大时,叶片中弦区的低无量纲温度区域的面积略微减小,而叶片前缘和尾缘的高无量纲温度区域的面积略微增大,这说明主流出口压力的增大会使涡轮叶片的无量纲温度略微增大。此外,主流出口压力的变化对涡轮叶片吸力面中弦区无量纲温度的影响相对于其他区域更大。经过计算可知,当主流出口压力从120 kPa增大到160 kPa时,涡轮叶片平均无量纲温度从0.873增大到了0.878,增大了0.57%。

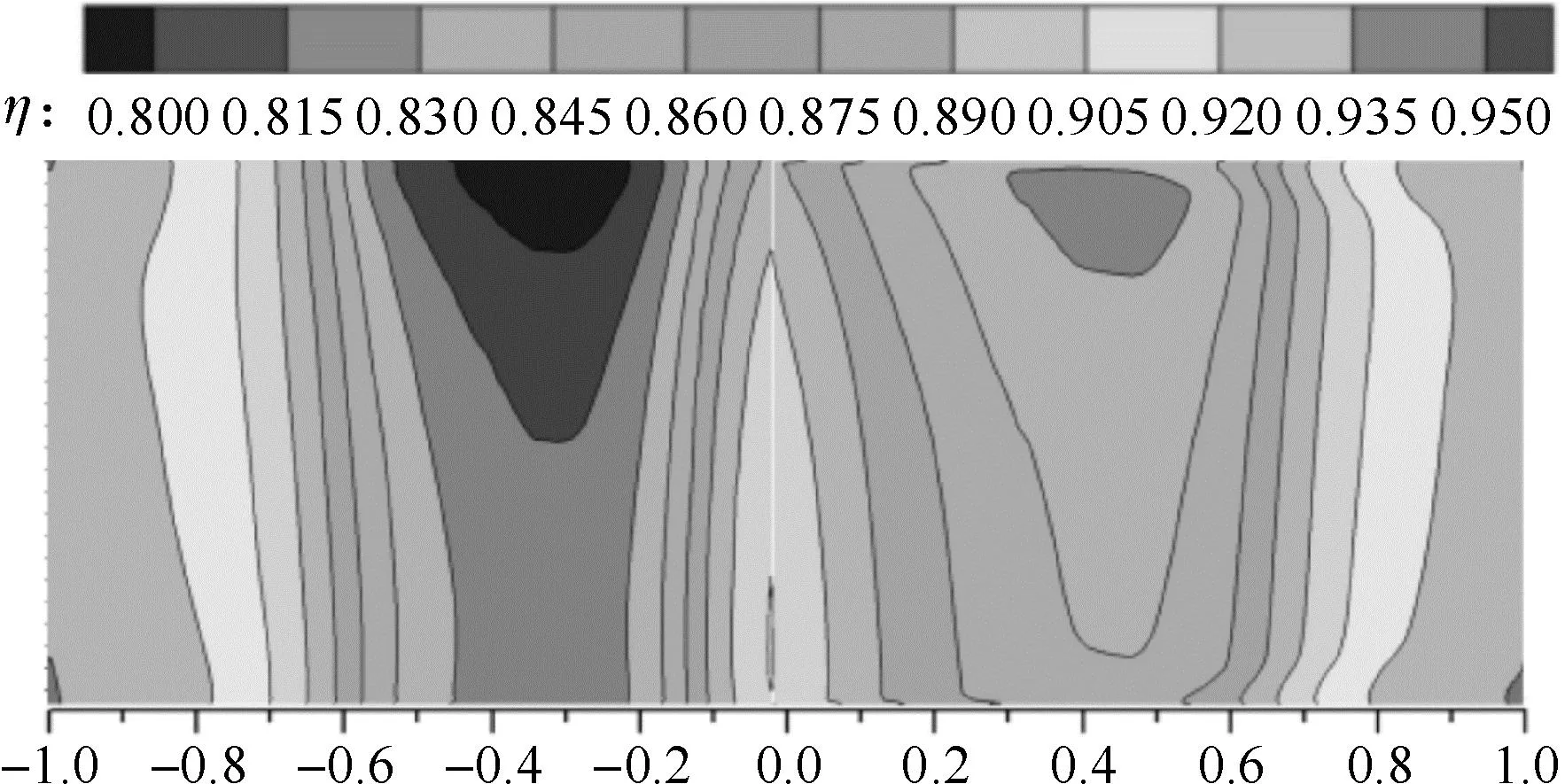
(a) pgo=120 kPa

2.2 主流进出口压比的影响

图7给出了主流进出口压比对涡轮叶片表面无量纲温度分布的影响,当主流进出口压比处于1.3～1.5时,涡轮叶片表面无量纲温度分布处于0.76～0.95。由图7(a)和图7(b)可知,当主流进出口压比增大时,涡轮叶片尾缘高无量纲温度区域的面积有所减小,叶片中弦区低无量纲温度区域的面积有所增大,而叶片前缘的无量纲温度分布变化的很小。当主流进出口压比增大时,在相对轴向弦长-0.2和0.9左右区域涡轮叶片无量纲温度分别降低约0.54%和1.53%,这说明主流进出口压比对叶片尾缘无量纲温度的影响大于叶片前缘和中弦区。经过计算可知,当主流进出口压比从1.3增大到1.5时,涡轮叶片平均无量纲温度从0.881降低到了0.871,降低了1.14%。

(a) pr=1.3

2.3 冷气与主流温度比的影响

图8给出了冷气与主流温度比对涡轮叶片表面无量纲温度分布的影响。当冷气与主流温度比Tr处于0.6～0.7时,叶片表面的无量纲温度分布处于0.76～0.94。由图8(a)和8(b)可知,当冷气与主流温度比增大时,涡轮叶片表面的无量纲温度均有所提高,具体表现在叶片中弦区的低无量纲温度区域的面积有所减小,而叶片前缘和尾缘的高无量纲温度区域的面积略微增大。这是由于在其余设计参数保持不变的情况下,增大冷气与主流温度比会提高冷却气流的温度,而冷气温度的增大虽然会提高叶片的冷却效率,但会使得叶片表面温度的降低更加困难。冷气与主流温度比对叶片中弦区无量纲温度的影响最大,随后是叶片的前缘和尾缘。当冷气与主流温度比增大时,在相对轴向弦长-0.3、0.5和0.9左右区域涡轮叶片表面无量纲温度分别增大了6%、4%和2%左右。经过计算可知,当冷气与主流温度比从0.6增大到0.7时,涡轮叶片的平均无量纲温度从0.864增长到了0.889,提高了2.81%。

(a) Tr=0.6

2.4 冷气与主流流量比的影响

图9给出了冷气与主流流量比乘以100即Mr对涡轮叶片表面无量纲温度分布的影响。由图9(a)和9(b)可知,当Mr为3时,涡轮叶片表面无量纲温度分布为0.82～0.95;当Mr为8时,涡轮叶片表面无量纲温度分布为0.77～0.94。这说明Mr的增大会极大地降低涡轮叶片表面的无量纲温度,当Mr增大时,涡轮叶片表面无量纲温度有所下降,具体表现在涡轮叶片表面低无量纲温度区域的面积有所增大,高无量纲温度区域的面积有所减小。Mr的增大对叶片中弦区无量纲温度的影响最大,随后是叶片的前缘和尾缘。当Mr从3增大到8时,在相对轴向弦长-0.1和0.6左右区域涡轮叶片表面无量纲温度分别降低了约5%和4%。经过计算可知,当Mr从3增大到8时,涡轮叶片平均无量纲温度从0.896降低到了0.863,降低了3.68%。

(a) Mr=3

2.5 响应面模型拟合公式

表2给出了二阶响应面模型的系数,具体响应面模型拟合公式详见1.4节公式(6)。经过计算可知,拟合得到的有关涡轮叶片平均无量纲温度响应面拟合公式的决定系数为0.99,均方根误差为0.000 37。图10给出了响应面拟合公式偏差,由图10可知,数值得到的涡轮叶片平均无量纲温度和采用响应面模型得到的涡轮叶片无量纲温度之间的标准化残差均小于4%,偏差绝对值的平均值为1.63%。这说明采用试验设计和响应面模型得到的经验公式具有较高的精度和较低的误差。此外,公式(6)的适用范围为:690 K≤Tgi≤710 K,120 kPa≤pgo≤140 kPa,1.3≤pr≤1.5,0.6≤Tr≤0.7,3≤Mr≤8。

表2 响应面模型的系数

图10 响应面拟合公式偏差

采用中心复合设计(CCD)-响应面法(RSM)获得了不同设计参数(Tgi、pgo、pr、Tr和Mr)下涡轮叶片平均无量纲温度ηave,并对设计参数的显著性进行了分析。图11给出了涡轮叶片平均无量纲温度的Pareto效应图和正态效应图。在Pareto效应图中,正效应分布在图中线条的右方,负效应分布在线条的左方。在正态效应图中,各因子的效应由小到大排成序列,并显示了各个设计参数的显著性。从图11可以看出,由灵敏度水平从高到低排列的涡轮叶片平均无量纲温度的有效项依次是Mr、pr、Tr、pr×Mr、pgo、Mr×Mr、Tr×Mr、pgo×Mr和pgo×pr。其中pr、pr×Mr、pgo、Mr×Mr、Tr×Mr和pgo×Mr对涡轮叶片平均无量纲温度有正效应,Mr、Tr和pgo×pr对涡轮叶片平均无量纲温度有负效应。在五个设计参数Tgi、pgo、pr、Tr和Mr中,Mr是影响涡轮叶片平均无量纲温度的最显著参数,其次是pr、Tr和pgo,而Tgi几乎没有影响。