基于“数学化”思想对统领课教学的多维度探究

包雯

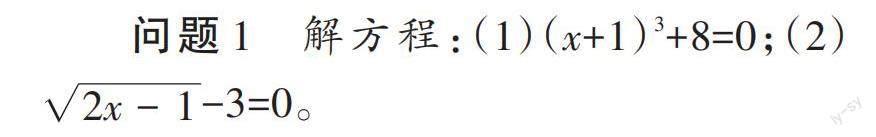
一、教學内容分析

统领课是一章内容正式授课的第一节课，对全章框架、内容、方法、思维等要素进行梳理，是承载整章教学内容的先导课，具有统摄作用，旨在让学生“先见森林，再见树木”。

一元二次方程知识量大，复杂程度高，是更深层次上对实际问题中含有未知数的等量关系的表达方式，也是继续学习一元二次不等式、二次函数及二次曲线的重要基础。教师要加强对单元统领课的重视和研究，从培养学生核心素养的角度让学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。

二、设计理念

弗赖登塔尔将“数学化”分为水平数学化和垂直数学化两种形式。水平数学化，是学生可以运用教学工具发现和解答生活情境中的问题；垂直数学化，是在数学系统内再组织的过程。简单来说，水平数学化是从现实世界走进符号世界，而垂直数学化是在符号世界中前进。教师对两种数学化重视程度有差异，会在教学实践中发生权重分配上的偏差。因此，两种不同维度的数学化如何合理地分配权重，也需要根据具体教学内容进行微调。就一元二次方程统领课而言，教师既要引导学生提炼实际问题中的数学成分，将实际问题向数学问题转化，让学生经历“分析→提炼→抽象”的过程，实现水平数学化的顺利过渡；也要引导学生对研究策略和路径进行迁移，建立垂直数学化的探究路径，培养学生的数学思维方式，渗透数学思想方法。

三、教学过程

1.水平数学化

（1）创设教学情境，让学生学会用数学眼光观察现实世界

情境 小明购买了16m的篱笆，计划围一个矩形花圃。看着12m的围墙，小明陷入了沉思……

【设计意图】设计的情境开放程度大，入口宽，学生极有可能“走”向二次函数。如何从函数一步步“走”进二次方程，对教师课堂应变能力是极大的考验。如此开放的设计，是希望最大限度引导学生用“数学眼光”观察现实世界，提出有“数学味道”的实际问题，将实际情境与数学表征进行转化。

（2）设计问题串，让学生学会用数学思维思考现实世界

师：怎样围才能使矩形花圃的面积最大？试一试。

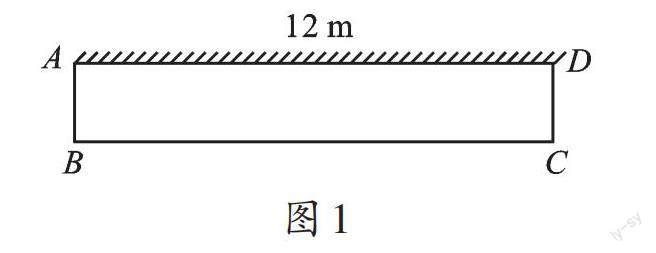
生1（预设）：从充分利用围墙的角度考虑，如图1，当AB=2时， S最大，S=24。

师：这时面积是最大的吗？

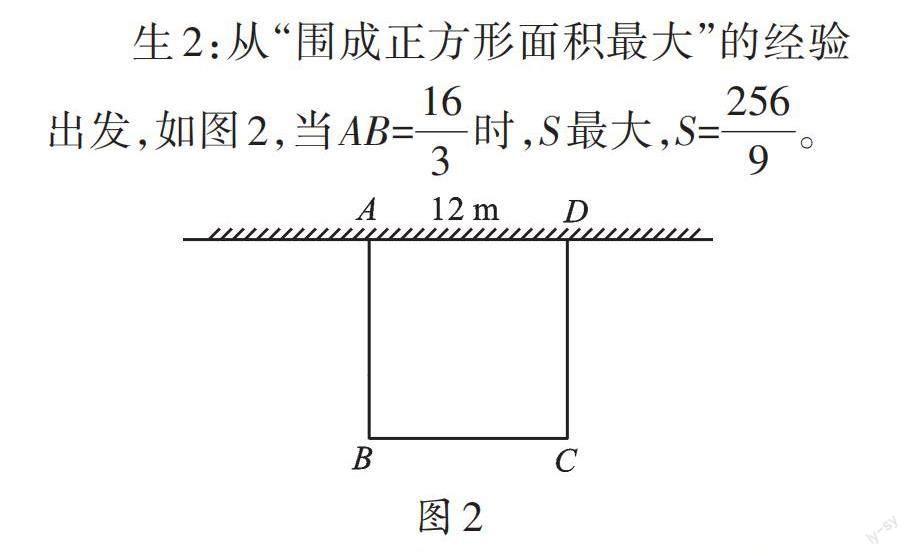
生2：从“围成正方形面积最大”的经验出发，如图2，当AB=[163]时，S最大，S=[2569]。

师：这是最大的面积吗？还能围成其他形式的矩形吗？有多少种可能？

师：你还能找出比图2面积更大的矩形吗？试一试。

【设计意图】如果仅停留在“最大化”的问题上，本题只能算是带有数学味道的“生活化”问题。教师应顺着学生的想法，沿着“最大化”这一优化路径，引导学生尝试、探究，在反复试错中找到解决问题的数学工具，促进学生深度思考。学生通过反复计算，在试图找出“最大化”方案的过程中，将生活化问题抽象成数学问题，在这个过程中，学生思维已经从“生活化”转向“数学化”。

（3）建立数学模型，让学生学会用数学语言表达现实世界

通过尝试，学生发现，无论是“充分利用墙的长度”，还是“围成正方形”，都不能使围成的矩形面积最大。

生3：根据运用方程解决问题的经验，我们可以设AB=xm，BC=（16-2x）m，面积为x（16-2x）=-2x2+16x=-2（x-4）2+32，当x=4时，面积最大，为32。

【设计意图】“围花圃”这一情境的创设，让学生经历从生活世界走向符号世界，经历将实际问题转化为数学问题的过程。从“用数学的眼光观察现实世界”，到“用数学的思维思考现实世界”，再到“用数学的语言表达现实世界”，学生结合已有经验形成功能更强、结构更复杂的新模型。

2.垂直数学化

（1）从数学概念到新数学概念的平行结构探究，完成“整式方程”体系的完整建构

师：这是我们学过的方程吗？我们学过哪些方程？你可以给这个方程下个定义吗？整式方程的命名通常遵循什么规则？

【设计意图】教师通过引导学生对一元二次方程概念内涵的类比研究，渗透类比思想，使学生对方程中涉及的“多元”“高次”有了进一步认知，同时完善整式方程和分式方程的概念体系，为更多类型方程的探究奠定了基础，也为探究一元二次方程提供了一致的探究路径，进而推广到对整式方程概念内涵的探索。

（2）探究路径的迁移

师：我们对一元二次方程可以进行哪些方面的研究？

【设计意图】教师引导学生将方程的研究策略和研究路径进行迁移，即：定义→解→解法→应用，确立“垂直数学化”这一预设目标，让学生建立一般化的研究策略、路径，对一元二次方程做进一步探究。

（3）在“消元”和“降次”两个方面统一化归思想

师：回顾其他方程的解法，你怎么求解一元二次方程？怎样降次？这些“降次”的方法适用其他一元二次方程吗？

【设计意图】结合“消元”“化整”的经验，学生顺理成章地将“化归”思想迁移，“降次”应运而生。

（4）对比研究，完善方程“解法系统”的完整性建构

问题1 解方程：（1）（x+1）3+8=0；（2）[2x-1]-3=0。

师：这些方程的解法有什么共同的数学思想吗？

【设计意图】从“一元”到“多元”、从“一次”到“高次”、从“有理”到“无理”，学生经历不同方程解法的对比分析过程，发现不同解法中蕴含着相同思想——“化归”思想，完善方程“解法系统”的完整性建构，实现数学思想的再度升华。

（5）建立方程与函数的联系，培养学生数学“区块链”意识

师：是否可以围成比32m2更大的矩形呢？随着x的变化，S也在变化，怎样才能围成最大矩形？

【设计意图】回归问题情境，让学生体会方程是用来刻画现实世界的模型，也是用于解决现实问题的数学工具。通过引导学生对数量关系中“变化而变化”的思考，学生主动挖掘新函数模型，建立方程和函数“区块链”的意识。

四、结合教学实践对统领课的再思考

1.一盏明灯破“暗处”

良好的统领课教学可以帮助学生建立知识框架，提高学习效率，厘清本章所涉及的基本数学问题、数学方法和数学思想。同时，学生可以站在一个更高的位置，纵观全局，无论对水平知识体系的横向迁移，还是对垂直知识体系的纵深推进，都能得心应手。统领课教学就是“先见林，再见树”；如一盏“明灯”，为后续学习指明方向，它照亮了数学学习之路，让学生更加明确做什么、怎样做以及为什么。

2.添砖加瓦筑“新巢”

当然，统领课只明确学习主线和方向远远不够，更应结合相互关联的“区块链”，引导学生主动对数学知识、数学模型及数学思想进行“链接”，对数学知识乃至整个数学系统溯本求源，在激发学生探究欲望的同时，也让学生感受数学思想方法的美妙之处。通过一步步、一层层的探索，对比，联结，数学知识系统变得更加完整，数学方法变得更加完善，学生逐渐养成独特的“数学眼光”、深度的“数学思维”和精准的“数学表达”，从而最终落实数学核心素养的养成。

（作者单位：江苏省南京一中明发滨江分校）