新型线驱动式微创手术器械结构设计与运动学分析
2024-01-08赵万博陈赛旋姜官武
赵万博,陈赛旋,姜官武,李 荣,章 宇
(1. 上海工程技术大学 机械与汽车工程学院,上海 201620; 2. 西南科技大学 信息工程学院,四川 绵阳 621002;3. 苏州融萃特种机器人有限公司,江苏 苏州 215011)
微创手术(minimally invasive surgery, MIS)的概念于20世纪80年代提出[1]。与传统的开放式手术相比,MIS 极大地减小了对病人健康组织的创伤,缩短了术后恢复时间,因而在全球范围内得到了广泛应用。如今,MIS已成为外科医疗的重要发展方向之一。与此同时,伴随着机器人技术的飞速发展,MIS机器人系统应运而生,有效弥补了传统MIS的不足。现阶段,世界各国的科研机构和医疗机构均开展了MIS机器人的相关研究,其中手术器械的结构是研究的重点方向之一。
目前,已研制成功的微创手术器械按驱动方式可大致分为刚性连杆式、柔性线驱动式和柔性连续体式三类。例如:全球最具影响力的手术机器人系统——Da Vinci手术机器人系统,其系列产品均采用柔性线驱动式手术器械,可实现自转、俯仰、偏摆和开合四自由度的灵活运动[2]。Hong等[3]将3条相同的P-S-R(移动副-球面副-转动副)串联运动链并联起来组成手术器械的腕部机构,由此设计了一种四自由度手术器械;Choi等[4-5]开发的手术机器人具有6个自由度,该机器人运动灵活且有效载荷高,可用于单切口腹腔镜手术;Piccigallo 等[6]开发了一种带有双末端夹持装置的手术器械,每个夹持装置均有6个自由度,可通过直径为30 mm的体表切口进入人体内开展手术作业;Shang等[7]通过结合钢丝绳与多关节构型,研制了一种连续体手术操作钳;Rosen等[8]提出了一种单孔连续体手术器械,可应用于头部微创手术。此外,天津大学、哈尔滨工业大学以及上海交通大学等高等院校[9-11]针对自主研发的手术机器人系统进行了深入研究,分别设计了相应的线驱动式多自由度手术器械,以满足不同的医疗需求,从而提高手术效率及其安全性。
刚性连杆式手术器械的结构设计相对复杂,为实现多自由度运动,需要数量较多的机械零件,且其工作空间不具有优势;柔性连续体式手术器械虽能显著减小尺寸,且功能多样[12],但存在有效载荷较小、难以实现运动学建模等缺点[13]。而钢丝绳具有轻巧、占用空间小、操作方便、柔韧性强和抗拉强度高等优点,能够满足微创手术器械的使用要求,因此柔性线驱动式手术器械在手术机器人系统中的应用最为广泛。
然而,柔性线驱动式手术器械的各运动关节之间存在运动耦合的问题,即驱动一个关节运动时会引起其他关节的运动。针对该问题,现有解决方法通常分为2类:软件解耦和机械解耦。软件解耦是指通过设计相应的控制算法来协调手术器械各关节的运动,当产生耦合运动时,对相应关节施加等值反向的运动来进行补偿,以消除运动耦合。例如:Da Vinci手术机器人系统通过改进控制算法来实现其末端手术器械各关节的运动解耦[14];Xue等[15]采用基于前馈补偿的位置控制算法,将腹腔镜手术机器人驱动轮的转动角度的估计误差绝对值降低在4°以内;Cao 等[16]将神经优化控制方法与经验回放相结合,设计了一种蛇形机器人控制算法,提高了其运动性能和鲁棒性;Ma等[17]采用视觉伺服控制方法对自主研制的六自由度连续体手术器械的运动路径进行了优化,在扩大工作空间的同时提高了安全性。机械解耦是指通过改进或增加相应的机械结构来实时消除手术器械各关节在工作过程中的运动耦合。Jin等[18]针对手术器械的驱动装置,采用差动行星齿轮设计了一种解耦装置,该装置能够实时消除手术器械在工作过程中产生的运动耦合;闫昱晟等[19]提出了一种对称式腕部结构以及一种与钢丝绳轨道平行对称的绕线布局方式,并通过优化主要尺寸参数的方式减少了手术器械各关节的耦合运动;Niu等[20]提出了一种由基于模块化设计的球形远心运动机构组成的MIS机器人,并通过改进手术器械中钢丝绳的走丝方式实现了偏摆关节与末端夹持器的运动解耦。
综上可知,通过软件解耦可以降低手术器械结构复杂度及其制造成本和装配成本,但要针对不同的手术器械开发、匹配相应的解耦算法。另外,若手术机器人系统中的电子元器件受到干扰,则会产生算法误差。而机械解耦可将手术机器人系统的软件与硬件独立开来,使得其控制系统的整体性更强,同时可避免因电子元器件受干扰而产生的算法误差,保证了系统的可靠性和安全性。
基于此,针对传统线驱动式手术器械各关节存在运动耦合的问题,笔者拟从机械结构出发来进行解耦设计,提出了一种新型的四自由度线驱动式手术器械,其偏摆关节采用行星齿轮式结构来实现偏摆运动,具有关节运动耦合性低的优点。
1 新型线驱动式手术器械设计
1.1 手术器械整体结构设计与驱动绳布置
按照MIS机器人的设计要求,手术器械须具备4 个自由度:自转、偏摆、俯仰和开合。基于此,设计了一种新型的四自由度线驱动式手术器械,其整体结构如图1所示,主要由驱动装置、连杆和末端夹持装置三部分组成。其中,驱动装置位于手术器械的前端,采用钢丝绳对连杆和末端夹持装置整体进行驱动。
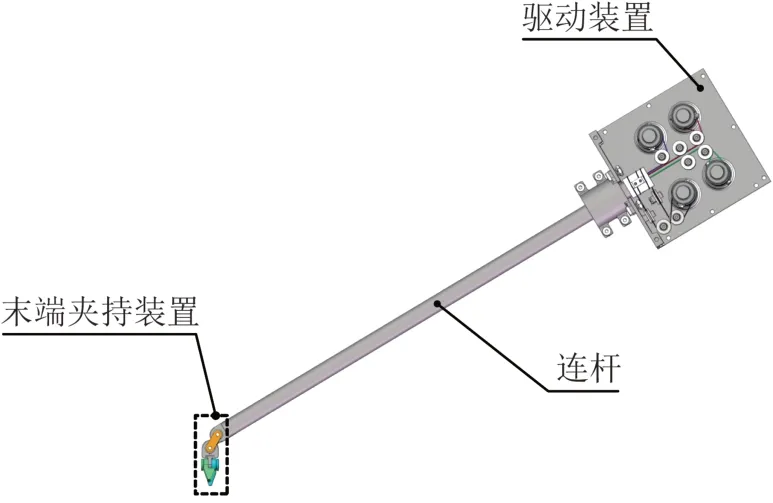
图1 新型线驱动式手术器械整体结构Fig.1 Overall structure of new cable-driven surgical in‐strument
在新型手术器械中,完成手术操作的零部件为连杆和末端夹持装置。其中,夹持钳爪1和夹持钳爪2作为俯仰关节,分别与偏摆关节和连杆组成三自由度串联机构,则整个手术器械可看作由2个相同的三自由度串联机构组成。如图2所示,所设计的手术器械的4个自由度为夹持器的俯仰和开合自由度、连杆的自转自由度以及偏摆关节的偏摆自由度。
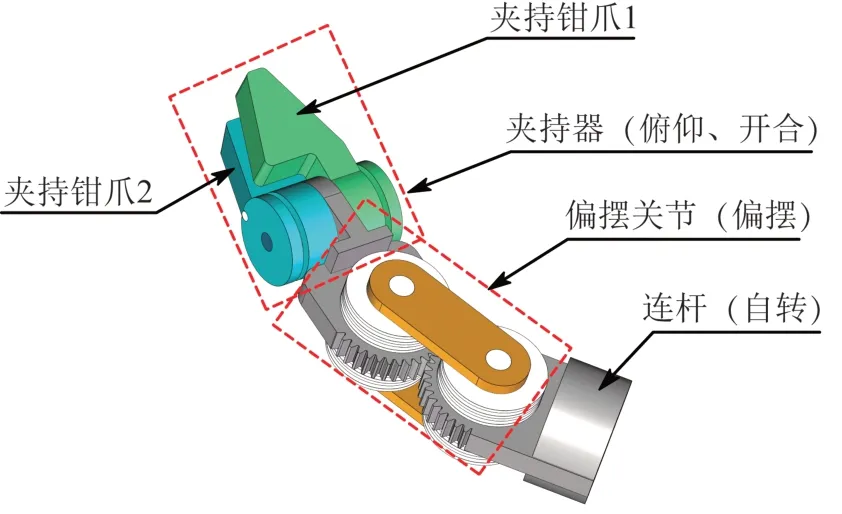
图2 新型线驱动式手术器械的自由度分布Fig.2 Distribution of degree of freedom of new cabledriven surgical instrument
新型手术器械中夹持器、偏摆关节和连杆的驱动绳的排布方式分别如图3至图5所示。钢丝绳通过绳结固定在手术器械的各个部位,每条钢丝绳均在各自的导向轨道内独立运动,不会相互干涉。如图3所示,夹持器的2个夹持钳爪分别配备了1条钢丝绳和相应的驱动电机,可实现对每个夹持钳爪的独立驱动;2条钢丝绳的导向轮组设计为上下对称的双层布置形式,上、下两层的导向轮分别将钢丝绳1和钢丝绳2引导至夹持钳爪1和夹持钳爪2处;驱动同一个夹持钳爪的钢丝绳在上、下两层导向轮上的布置轨迹对称。如图4 所示,钢丝绳3 单独驱动行星轮,以实现夹持器的偏摆运动。如图5所示,钢丝绳4缠绕在固定于连杆后端的套管上,拉动钢丝绳4的两端即可实现末端夹持装置整体的自转运动。
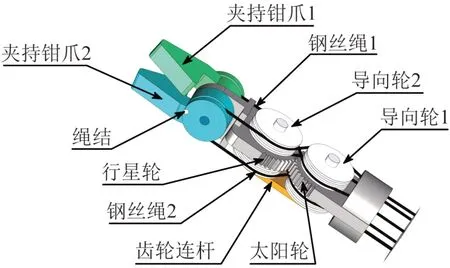
图3 夹持器驱动绳排布示意Fig.3 Arrangement schematic of driven cable for retainer

图4 偏摆关节驱动绳排布示意Fig.4 Arrangement schematic of driven cable for yaw joint

图5 连杆驱动绳排布示意Fig.5 Arrangement schematic of driven cable for con‐necting rod
1.2 驱动装置结构设计
新型线驱动式手术器械的驱动装置位于前端的驱动盒内,其结构如图6所示,主要包括基座、夹持钳爪1驱动绞轴、夹持钳爪2驱动绞轴、连杆驱动绞轴、偏摆关节驱动绞轴和导向轮组。如图7所示,钢丝绳两端反向螺旋缠绕在各驱动绞轴上,通过控制驱动绞轴的正反转即可实现手术器械每个关节2个方向的运动。其中:夹持器的2个夹持钳爪分别由2个绞轴独立驱动:当2个驱动绞轴同向旋转时,可实现夹持器的俯仰运动;当2个驱动绞轴反向旋转时,可实现夹持器的开合动作。
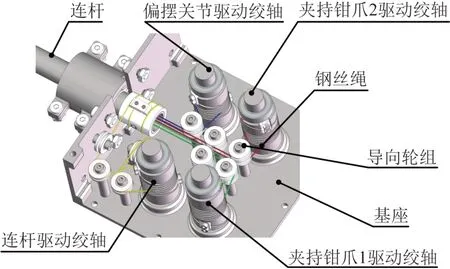
图6 驱动装置结构示意Fig.6 Schematic of driving device structure
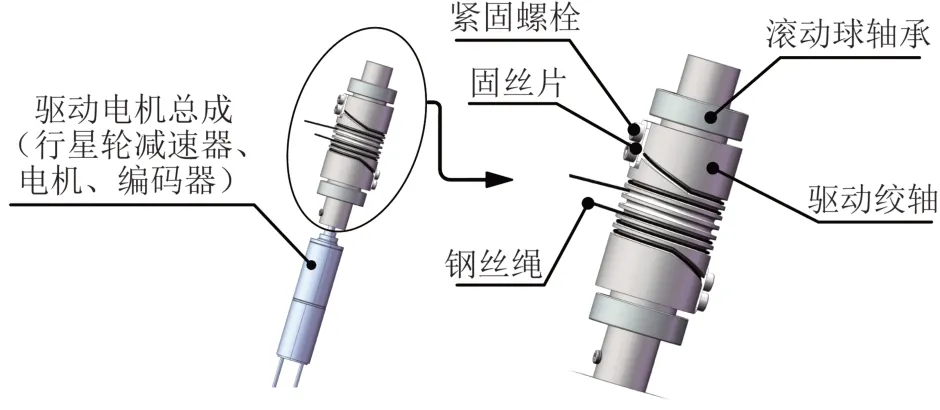
图7 驱动绞轴结构示意Fig.7 Schematic of driving hinge structure
2 线驱动式手术器械耦合分析与解耦设计
2.1 传统手术器械关节运动耦合分析
传统线驱动式手术器械的偏摆关节围绕一根转轴旋转,从而实现夹持器的偏摆运动,且驱动夹持器的2 条钢丝绳须同时经过偏摆关节上的导向轮。因此,当偏摆关节作偏摆运动时,驱动夹持器的钢丝绳会因受迫而产生形变,进而影响夹持器的运动。
为了方便分析传统手术器械各关节的运动耦合问题,将钢丝绳和导向轮绘制在同一平面中,选取驱动夹持钳爪1的钢丝绳1为例进行分析。如图8所示,假设夹持器的俯仰和开合自由度固定,仅令偏摆关节运动。
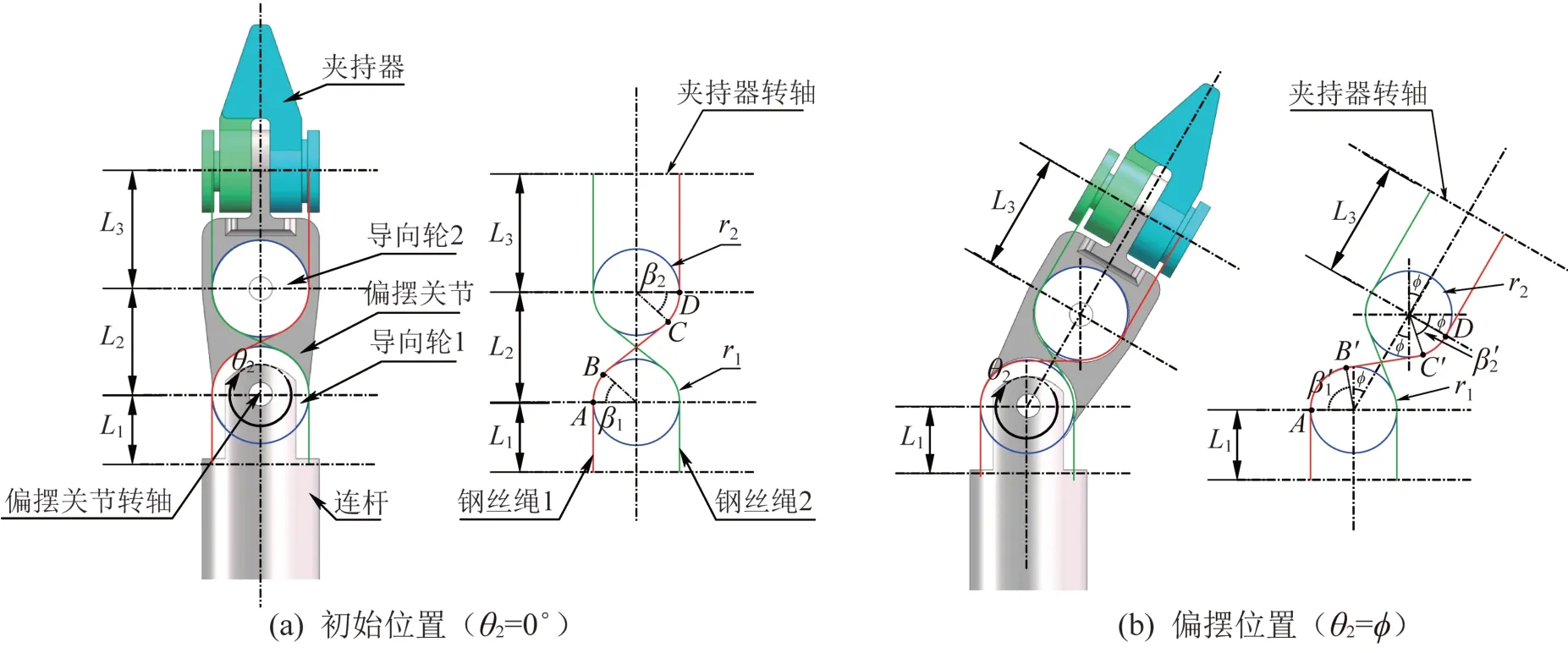
图8 传统线驱动式手术器械偏摆关节运动示意Fig.8 Schematic of motion of yaw joint of traditional cable-driven surgical instrument
由图8(a)可知,当传统手术器械处于初始位置(即偏摆关节转角θ2=0º)时,钢丝绳1 的长度C1可表示为:
式中:L1为钢丝绳经过导向轮1 之前的绳长,分别为钢丝绳1 在导向轮1、导向轮2 上的包络长度,为钢丝绳1 在导向轮1 与导向轮2 之间的长度,L3为钢丝绳经过导向轮2之后的绳长,r1、r2分别为导向轮1、导向轮2的有效半径,β1、β2分别为钢丝绳1在导向轮1、导向轮2上的包络角。
在本文中,r1=r2,故β1=β2,则钢丝绳1 的长度C1可表示为:
当偏摆关节顺时针转动ϕ时,钢丝绳1 的长度可表示为:
由图8(b)所示的几何关系可得,钢丝绳1 在导向轮1上的包络角变为:
联立式(2)和式(3)可得,偏摆关节转动前后钢丝绳1的长度变化量如下:
由于钢丝绳呈上下对称形式布置,因此钢丝绳1的实际形变量为2ϕr1。
通过上述分析可得,在传统手术器械偏摆关节的运动过程中,驱动夹持钳爪的钢丝绳的长度发生了变化,但钢丝绳在2组导向轮上包络的长度变化不均,导致偏摆关节与夹持器产生了运动耦合。
2.2 新型手术器械关节运动解耦原理
为了解决传统手术器械关节的运动耦合问题,以提高其运动控制精度,本文通过采用行星齿轮式结构和对称布置的钢丝绳相结合的方式来实现偏摆关节与夹持器的运动解耦。图9所示为新型线驱动式手术器械偏摆关节的运动示意。

图9 新型线驱动式手术器械偏摆关节运动示意Fig.9 Schematic of motion of yaw joint of new cable-driven surgical instrument
根据图9,当新型手术器械处于初始位置(即偏摆关节转角θ2=θ3=0º)时,钢丝绳1的长度C1与上文相同,即C1=L1+2β1r1+2r1cotβ1+L3。
当新型手术器械整体的偏摆角度为ϕ时,由行星齿轮传动原理可得偏摆关节的转角θ2=θ3=0.5ϕ,此时钢丝绳1的长度可表示为:
根据图9(b)所示的几何关系,可得钢丝绳1 在导向轮1上的包络角变为:
钢丝绳1在导向轮2上的包络角变为:
联立式(6)至式(8)可得,手术器械发生偏摆后钢丝绳1的长度可表示为:
由此可得,手术器械偏转前后钢丝绳1的长度变化量如下:
通过上述分析可知,采用行星齿轮式结构的偏摆关节在运动过程中能够使钢丝绳在导向轮上的包络长度的变化一致,从而实现运动解耦。
3 新型线驱动式手术器械运动学分析
在忽略行星齿轮传动误差的前提下,采用标准D-H 参数法构建新型线驱动式手术器械的正运动学模型,并通过解析法求得其逆运动学的封闭解。
3.1 正运动学模型
D-H参数法是一种常用的描述机器人关节运动的方法,可通过机器人各关节的转角来确定关节空间与笛卡尔空间的映射关系,进而确定机器人的位姿。
鉴于本文所设计的手术器械结构对称,选取由夹持钳爪1、偏摆关节和连杆组成的三自由度串联机构,建立其正运动学模型并开展分析。首先,移除手术器械中的钢丝绳和导向轮,将剩余刚性结构等效为开环链机构;然后,利用标准D-H 参数法建立关节转角与夹持钳爪1 位姿之间的关系。
在标准D-H 参数法中,机器人的每个关节均可由连杆长度ai、连杆扭转角αi、连杆偏距di和关节转角θi来描述。图10 所示为新型手术器械关节的D-H 坐标系。其中:θ1表示自转关节的转角;θ2、θ3(θ2=θ3)表示偏摆关节的转角,这是因为太阳轮和行星轮的分度圆半径和模数均相等,传动比z=1,故在运动过程中齿轮连杆相对于太阳轮的转角与行星轮相对于齿轮连杆的转角相等;θ4表示俯仰关节转角。该手术器械的D-H 参数如表1所示。
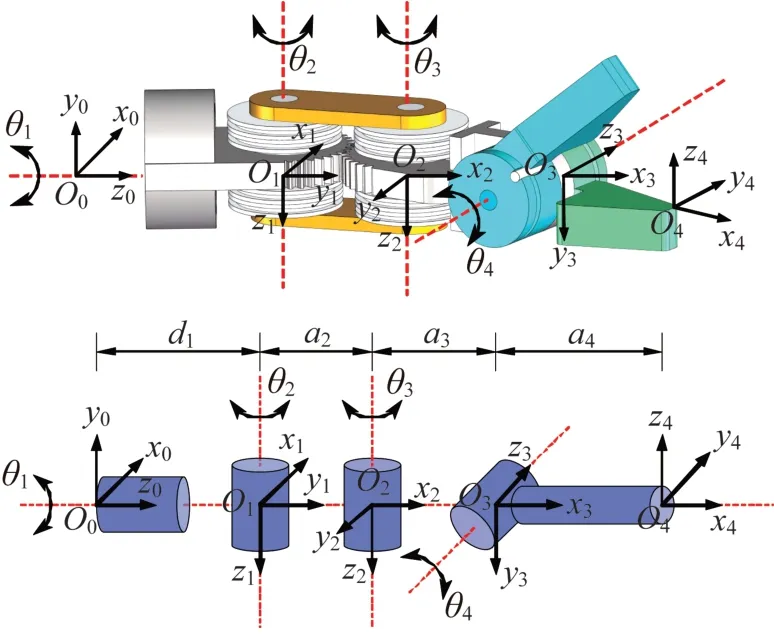
图10 新型线驱动式手术器械的D-H坐标系Fig.10 D-H coordinate system of new cable-driven surgical instrument
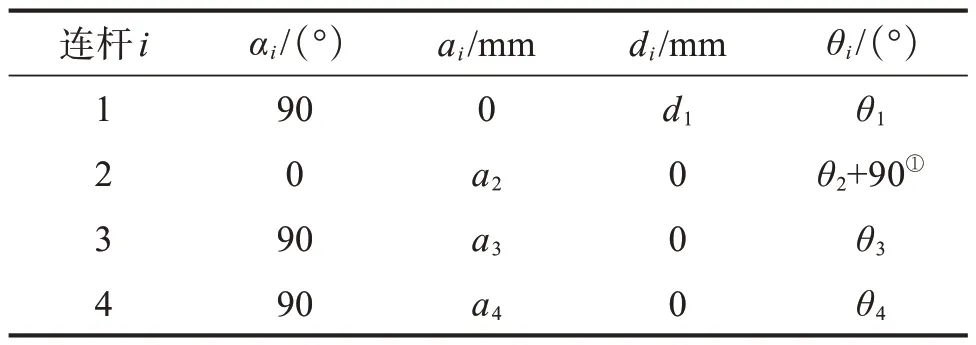
表1 新型线驱动式手术器械的D-H参数Table 1 D-H parameters of new cable-driven surgical in‐strument
在标准D-H参数法中,相邻连杆坐标系{i-1}与{i}之间的齐次变换矩阵可表示为:
式中:s表示sin,c表示cos。
利用表1中的D-H参数和式(11),计算得到手术器械各关节间的齐次变换矩阵,由此可得夹持钳爪1的位姿变换矩阵:
其中:
式中:px、py、pz分别为夹持钳爪1顶点在基坐标系O0-x0y0z0中的x、y、z坐标。
根据式(12),可得夹持钳爪1 相对于基坐标系O0-x0y0z0的位置矩阵P和姿态矩阵R:
3.2 逆运动学模型
在已知机器人末端位姿矩阵的基础上,计算机器人各关节的转角θi,可实现逆运动学求解。当机器人满足以下任意一个条件时,即可求得其逆运动学的封闭解[21-23]:
1)有3个相邻的关节转轴相交于一点;
2)有3个相邻的关节转轴相互平行。
本文所设计的手术器械满足第1个条件,基于上文夹持钳爪1的位姿矩阵,采用代数反解法进行求解,可得其运动学逆解:
式中:θ1∈[-180°, 180°],θ2=θ3∈[-60°, 60°],θ4∈ [-90°, 90°]。
3.3 电机驱动空间与关节转动空间之间的变换关系
传统机械臂的驱动电机位于运动关节处,而线驱动式手术器械的驱动电机安装在远离运动关节的驱动装置内,电机驱动装置内部的绞轴,继而带动缠绕于绞轴上的钢丝绳驱动对应的关节,以控制末端夹持器的位姿。为了有效操控线驱动式手术器械,须建立电机驱动空间与关节转动空间之间的变换关系。
本文所设计的手术器械由4条钢丝绳驱动,其传动原理如图11所示。
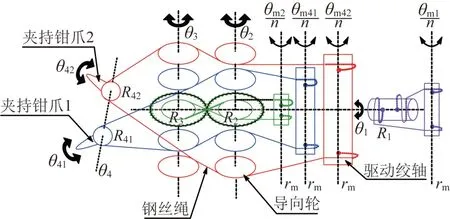
图11 新型线驱动式手术器械传动原理Fig.11 Transmission principle of new cable-driven surgical instrument
当夹持钳爪1 和夹持钳爪2 同时转动时(将夹持器看作一个整体,即2 个夹持钳爪的夹角为常量),则每个关节转角所对应的钢丝绳位移分别为:
式中:l1、l3、l41、l42分别为驱动各关节(自转关节、偏摆关节、俯仰关节1 和俯仰关节2)的4 条钢丝绳的位移,θ1、θ3、θ41、θ42为各关节转角,R1、R3、R41、R42分别为各关节的驱动半径。
根据图11 所示的手术器械传动原理,可得到各驱动电机转角θmi与对应关节转角θi的关系:
式中:n为减速器的减速比;rm为绞轴的驱动半径。
4 新型线驱动式手术器械运动学仿真分析
4.1 正运动学模型验证
利用MATLAB 软件中的Robotics Toolbox 来验证所构建的新型线驱动式手术器械正运动学模型的准确性。新型手术器械的D-H 参数的取值如下:d1=305 mm,a2=9.5 mm,a3=10 mm,a4=12.5 mm。 随机设定一组关节转角θi的值:θ1=60º,θ2=θ3=-30º,θ4=-22.5º。根据手术器械的D-H 参数,采用Robotics Toolbox 建立对应的连杆模型,在可视化界面中输入给定关节转角的值(即q1= 60°,q2=-30°,q3=-30°,q4= 22.5°)。如图12 所示,通过Robotics Toolbox 仿真计算得到夹持钳爪1的位置坐标 (x,y,z)=(15.848, 17.883, 324.001) mm;随后,将该组关节转角值代入上文建立的正运动学模型,可得:
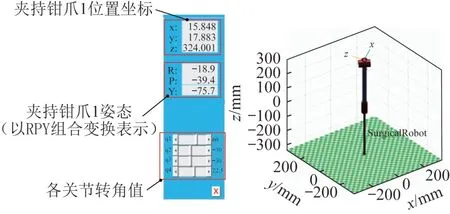
图12 新型线驱动式手术器械的位姿仿真结果Fig.12 Simulation results of position and posture of new ca‐ble-driven surgical instrument
根据式(16),计算得到夹持钳爪1 的位置坐标(px,py,pz) = (15.848 4, 17.883 2, 324.001 5) mm,这与通过Robotics Toolbox 仿真得到的位置坐标(x,y,z)基本一致。
在图12中,夹持钳爪1的姿态以RPY组合变换表示,其中R、P、Y分别表示夹持钳爪1坐标系相对于基坐标系的横滚(roll)、俯仰(pitch)和偏摆(yaw)三旋转组合变换。变换方式为:先绕基坐标系中的x轴旋转ψy(偏摆角),再绕y轴旋转ψp(俯仰角),最后绕z轴旋转ψy(横滚角)。基于所构建的正运动学模型,ψy、ψp、ψr的计算式如下:
基于式(16)可得:ox=0.25,nx=0.731 5,ay=0.749 0,az=0.191 3,nz=-0.634 4。将这些数值代入 式(17),计算得到:ψr=-18.868 6°,ψp=-39.374 1°,ψy=-75.668 7°,这与通过Robotics Toolbox仿真得到的夹持钳爪1的姿态基本一致。
综上,基于正运动学模型计算得到的夹持钳爪1的位置和姿态与通过Robotics Toolbox仿真计算得到的结果一致,验证了所构建的正运动学模型的准确性。
4.2 逆运动学模型验证
为了验证所构建的新型线驱动式手术器械逆运动学模型的准确性,首先,在MATLAB 软件的Simulink环境中建立图13所示的正、逆运动学函数模块,并根据关节转角的取值范围,基于正弦曲线将转角值(转换为弧度制)输入正运动学模块,计算得到夹持钳爪1的位姿矩阵;然后,将求得的位姿矩阵输入逆运动学模块,利用式(13)求得相应的关节转角;最后,将求得的关节转角与输入的关节转角进行比较,以确定误差。如图14所示,仿真结果表明,通过逆运动学模型计算得到的关节转角与输入值的误差极小,仅为10-16数量级,由此验证了所建立的逆运动学模型的准确性。
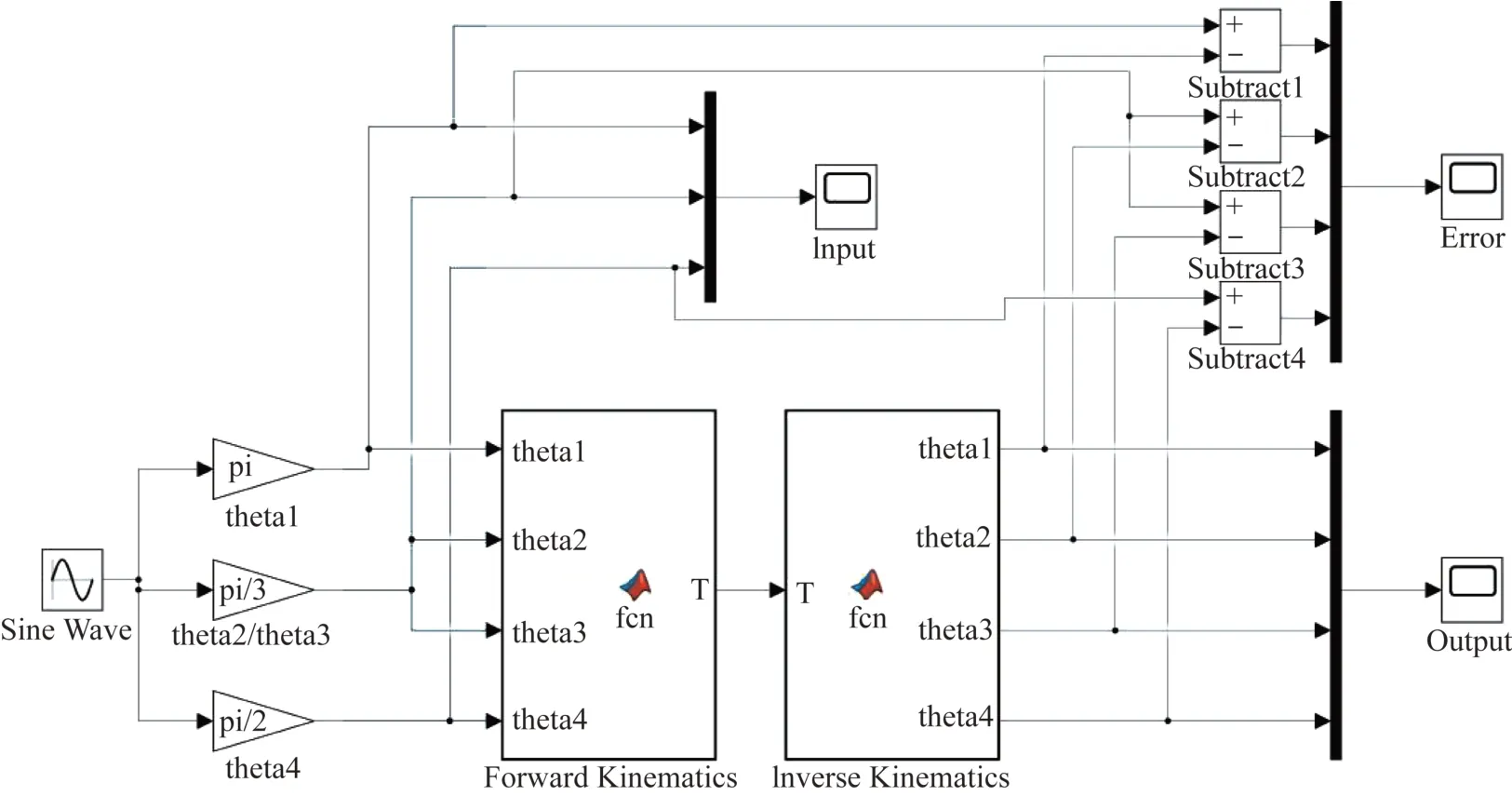
图13 新型线驱动式手术器械正、逆运动学的Simulink仿真模型Fig.13 Simulink model of forward and inverse kinematics of new cable-driven surgical instrument
4.3 工作空间分析
蒙特卡罗法(Monte Carlo method)是一种随机模拟方法,也称为统计模拟法或随机抽样技术。根据所设计的手术器械的结构参数和关节转角变化范围,结合蒙特卡罗法在关节转角范围内随机选取数值(本文采样点数量为1 000 000个),利用MATLAB 软件中的plot3 指令绘制采样点,由此得到该手术器械的工作空间,结果如图15 所示。由图15 可知,本文所设计的手术器械的工作空间满足微创外科手术的要求。
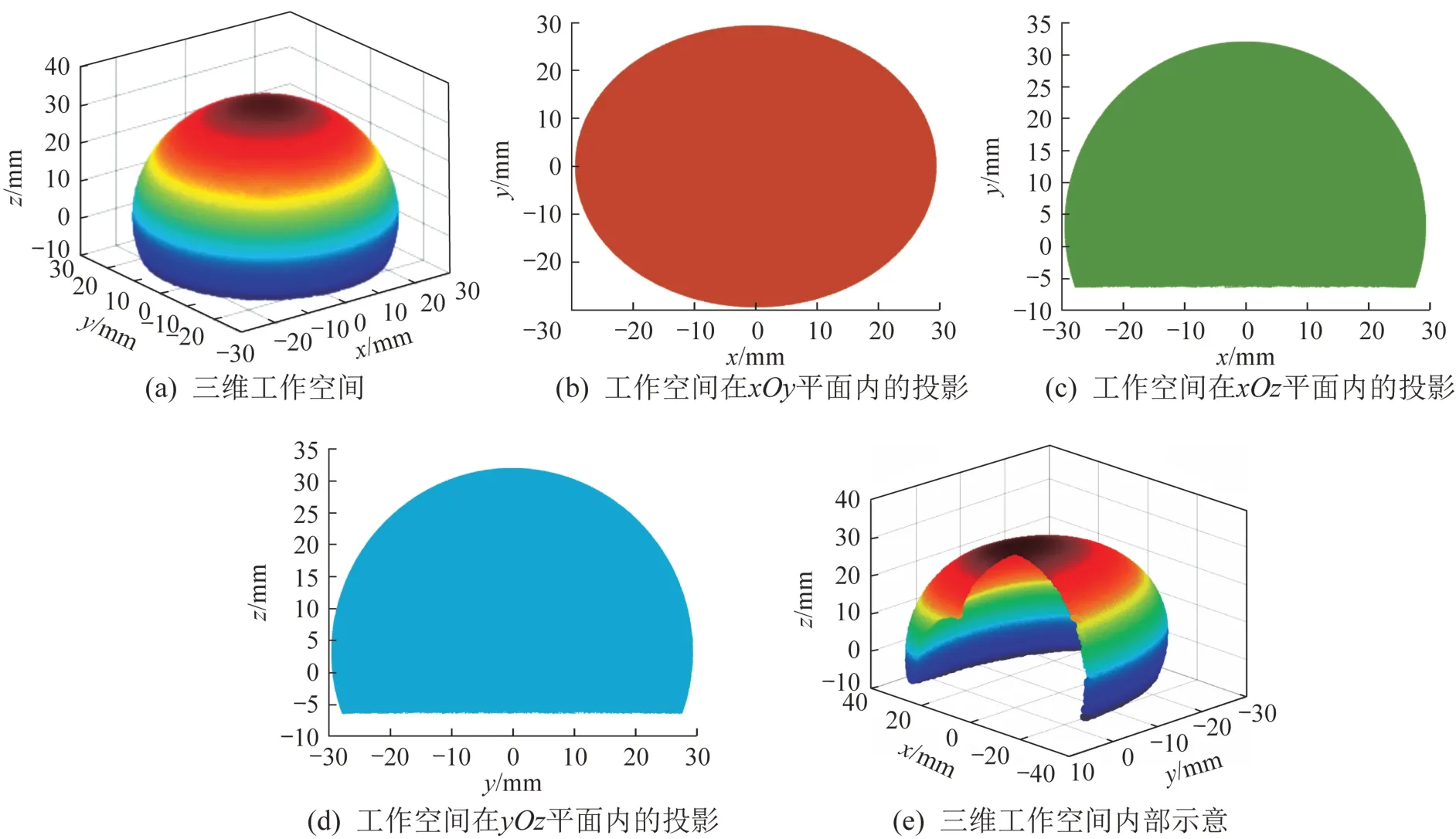
图15 新型线驱动式手术器械的工作空间Fig.15 Workspace of new cable-driven surgical instrument
5 结 论
1)本文设计了一种新型的线驱动式微创手术器械,其偏摆关节采用行星齿轮式结构。理论分析结果表明,该结构能够有效解决线驱动手术器械各关节之间存在的运动耦合问题。
2)基于所设计的手术器械的结构,建立了其正、逆运动学模型,并通过MATLAB软件验证了运动学模型的准确性;同时,对该手术器械的工作空间进行了分析。结果表明,所建立的运动学模型准确,且手术器械的工作空间能够满足微创外科手术的要求。
后续,将对所设计的手术器械的结构尺寸、动力学模型进行进一步优化,以及对降低行星齿轮式结构的传动误差进行进一步研究。
