基于深度学习的镇江地区土层剪切波速预测

2024-01-08徐为海许程吴晓亮苗永红

城市勘测 2023年6期

徐为海,许程,吴晓亮,苗永红

(1.镇江市勘察测绘研究院有限公司,江苏镇江 212000; 2.江苏大学,江苏镇江 212000)

0 引言

在建筑抗震设计中,场地类别直接影响工程的造价,故准确判定场地类别显得尤为重要。根据相关规范[1],通常根据不同深度土层的剪切波速再根据覆盖层厚度以计算场地的等效剪切波速,对工程场地的类别进行划分。因此,确定土层剪切波速是勘察中一项十分重要的环节。

目前获得地层的剪切波速主要有实测波速法,查表估值法以及经验公式法等。其中实测波速法适用各类情况,测试结果较为准确客观,但测试过程耗时耗力,且受场地、环境等条件限制;查表估值法和经验公式计算法未考虑区域地层特性影响,一定程度上受计算参数限制,估算结果缺乏客观性。除上述方法外,寻找一种可靠、准确,易于获得土层剪切波速的方法,对客观精确地判别场地类别具有重要意义。

近年来,基于各类深度学习的算法广泛应用于工程建设中[2,3]。其中,BP神经网络广泛运用于岩土工程领域的各种参数的预测,徐鹏逍根据BP神经网络理论,建立了包含地层分布和岩土参数的钻孔间岩土参数预测专家系统[4];欧阳磊等建立了以常规物理参数为输入变量,以压缩系数为输出向量的BP神经网络预测模型,并通过遗传算法优化模型,提高了预测性[5]。随机森林算法因为其高精度的优势,亦被广泛应用于各岩土工程领域[6,7];胡毅等运用随机森林算法对混凝土抗压强度进行了分析,得到该算法优于其他模型的结论[8];许飞青等针对原有模型无法有效处理多重因子之间的相互影响的问题,利用随机森林算法对当地水质进行了评价分析,结果证明随机森林算法对水质评价具有更高的准确性和灵敏度[9]。

土层剪切波速值和其他物理力学参数同为反映土层刚度特性的重要指标,大量研究表明,土层的物理力学性质和埋深与剪切波速有很强的关联性[10,11],各参数与剪切波速间呈非线性关系,而BP神经网络和随机森林两种算法均具有处理类似非线性映射关系的优势。

为寻求一种更加高效、精确预测土层剪切波速值的方法,以镇江地区的土层为例,尝试构建通过土层的物理力学参数对土层剪切波速进行预测的BP神经网络和随机森林两种深度学习模型,并对预测值进行验证,探索深度学习法在土层剪切波速分析方面的可行性。

1 剪切波速确定方法

1.1 实测法

实测法根据震源位置不同分为地面敲击法和孔中自激自收法,目前实践中,一般采用孔中自激自收的悬挂式波速测井法进行测试。该方法是利用钻孔中的浆液作为耦合剂,用电磁震源垂直于井壁作用一瞬时冲击力,在井壁处产生剪切波和压缩波。

该方法较地面敲击法简便易行,但由于该测试方法需要以测试孔中水、泥浆等液体为耦合剂,在实际使用过程中有时较为不便。如在镇江地区分布较广的下蜀土层中钻进时无须泥浆护壁,且由于该地层为不透水层,钻进过程中孔中基本干燥,波速测试时需在钻孔中灌满水方可测试;有些地区场地局部分布易漏水的碎石层,该类场地内的钻孔存水(浆)困难,实测波速较难开展。

此外,实测波速尚受其他条件限制。根据陈卓识等人的研究,场地噪音和数据处理方法是导致剪切波速测试不确定性的重要因素[12];由于勘察施工过程中较多情况需使用套管以保证孔壁稳定,常常在有孔内钢套管的情况下进行测试,根据钟梁等的研究,套管的材料、长度均对实测波速值有影响[13]。

综上所述,实测法受场地环境、地层等各类因素影响较大;在条件不利场地进行实测时,波速测试有一定困难,且考虑外界不利因素干扰,测得的波速值必要时也需要进行修正、检查、验证后方可使用。

1.2 经验法

经验法一般通过建立剪切波速与标准贯入锤击数[14]或深度[15]等参数的回归关系式,该类方法通常具有较强的地区适用性。镇江地区经常采用的《南京地区地基基础设计规范》,对于粉质黏土中的剪切波速关系为:

vs=105N0.30

(1)

式中:vs—剪切波速(m/s);

N—标准贯入试验锤击数实测值。

类似式(1)经验法,由于各地土层的差异性,只能在某些限定的地区使用,且较难反映土层的物理力学参数与剪切波速的非线性关系。

2 深度学习法

2.1 BP神经网络

应用最广泛的BP(back propagation)神经网络是一种多层前向型神经网络,其训练方法多采用误差逆向传播算法。其过程有两个重要环节,在前向传递中,输入参数值从输入层经逐步处理直至输出层,每一层的神经元仅影响下一层,中间层(即隐含层)神经元负责将接收到的信息进行处理后传递至输出层;如果输出层得不到期望输出,则转入反向传播过程,网络将误差沿原来的连接通路反传回去,根据预测误差调整网络的权值和阈值,从而使BP神经网络输出不断逼近期望输出,当输出的误差减小到期望程度或者达到预先所设的学习迭代次数时,此时BP神经网络完成学习。

神经网络中最基本的成分是神经元,其数学模型为:

(2)

式中:yj为神经元j的输出;

x1,x2…xn为神经元i的输入;

wij为神经元之间的连接权值;

aj为神经元的阈值;

f(……)为输入到输出传递函数(也称激活函数)。

当神经元接收到n个来自其他神经元的输入参数,这些输入参数通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过“激活函数”处理即产生神经元的输出,输出即为下一个神经元的输入。多层神经元叠加后,就组成了完整的BP神经网络,可以进行复杂的输入和输出深度学习。

2.2 随机森林

随机森林是由Breiman于2001年提出的一种基于分类树的组合算法[16],可以用于分类和回归分析,通过集成多棵决策树来预测目标变量。随机森林回归能解释多个自变量对因变量的影响。

在用于回归分析时,假设有数据集(X,Y),其中X为输入变量,Y为输出变量。随机森林通过bootstrap抽样法,由回归树θ构成组合模型{h(X,θk),k=1,2,…,K},通过K轮的集合训练,得到预测序列{h(X,θ1),h(X,θ2),…,h(X,θk)},从而可以构建预测模型,其最终值为所有决策树输出的平均值,其表达式为:

(3)

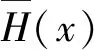
hi(x)为单科决策树模型;

Y为输出变量;

k为模型中决策树的个数。

2.3 主要数据分析过程

本文以镇江地区的土层为研究对象,通过搜集近20多年的典型室内相关资料,筛选共同包括土层物理力学指标和实测波速指标构成数组。其分析过程如下:

(1)选取资料中同时进行实测波速试验和取土样的钻孔,将某深度处同时包含的波速实测值及相应的物理力学参数构成数组。

(2)筛选的每组数据包括含水量、密度、比重、液塑性指数,压缩指标的近800组样本,可使得模型得到充分训练。

(3)考虑实用性选用上述的6个参数和深度共7类参数组成输入变量,以剪切波速值为输出变量,每组数据的范围如表1所示。

表1 场地土的物理力学指标和剪切波速范围

(4)筛选的数据集在模型训练过程中均进行归一化处理,对原始数据的线性变换,将其映射至[0,1]之间,其方法如下:

设变量x=(x(1),x(2),…x(n))

变量x至变量y的数据变换为:

f(x(k))=y(k),k=1,2,…,n

归一化:

(4)

式中:minx(k)和maxx(k)分别为序列的最小和最大值。

3 深度学习模型建立及评价

3.1 BP神经网络预测模型

通过数据分析,并考虑网络模型的实用性,本模型采用1个隐含层即可满足精度要求。隐含层神经元个数对BP神经网络的性能影响较大,一般隐含层神经元个数范围按式(5)确定,

(5)

式中:k—隐含层神经元个数;m—输入层神经元个数;n—输出层神经元个数;q—0～10之间的常数。

本模型输入层变量为7个,输出层变量1个(详见表1),根据式(5),隐含层的神经元个数在3～13个为宜。

由图1可见,当隐含层神经元个数为8时,决定系数均值最大,表示此时模型性能最佳。为了降低初始权值和阈值对预测值的影响,在神经网络训练时选取运行10次所得决定系数的平均值作为模型的评价指标。

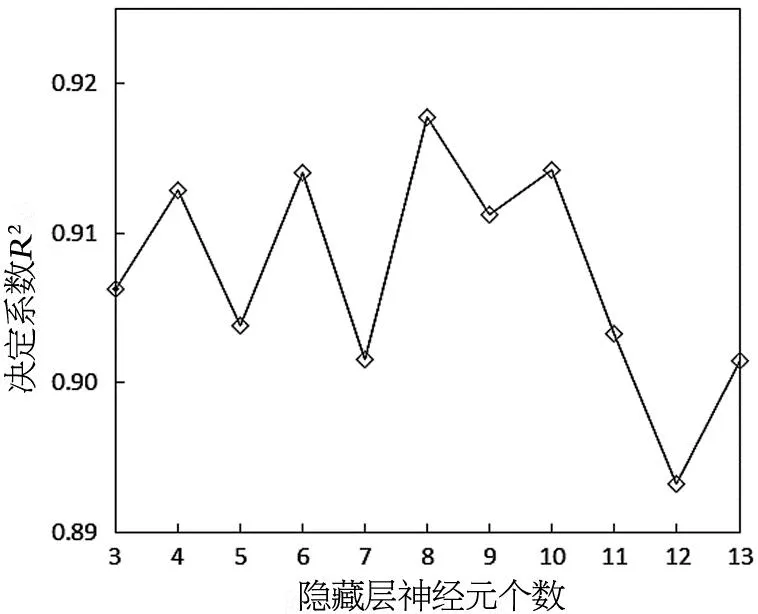
图1 隐含层神经元个数与决定系数的关系

经学习,确定采用含有8个神经元的单隐含层BP神经网络模型。

3.2 随机森林预测模型

随机森林模型中主要涉及决策树数量ntree和最小叶子数mtry两个重要参数。决策树数量影响随机森林的训练度和精确度,通常决策树数量越多,模型的精确度越高;最小叶子数影响随机模型的扰动程度,在回归模型中该数一般按式(6)取值。

(6)

式中:P为变量个数。

随机森林回归算法主要通过袋外数据误差来选定参数,当决策树数量ntree设置为300时,树的数量与均方根误差的关系如图2所示,在决策树数量达到150时误差曲线已达到最低位置并与横轴近乎平行,误差值趋稳,故本模型ntree值取150。

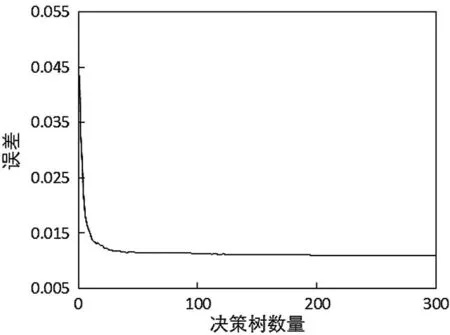
图2 树的数量与均方误差关系

本模型变量个数为8个,根据式(6)最小叶子数mtry取2或3为宜。为确定最优mtry值,取模型训练10次的平均均方根误差最小值所对应的参数为最优mtry值,结果如图3所示,当叶子数为1时决定系数最佳,表示此时模型效果最好,故本模型mtry值取1。

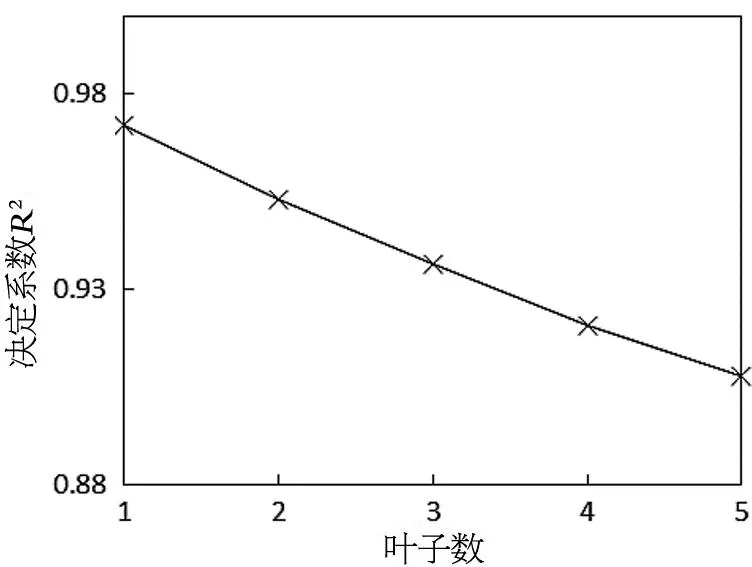
图3 叶子数与决定系数关系

3.3深度学习模型的评价

BP神经网络和随机森林模型均采用K折交叉验证法进行评价,模型性能以决定系数,均方根误差,平均绝对误差和运行时间等指标进行对比评价,结果如表2和图4所示。

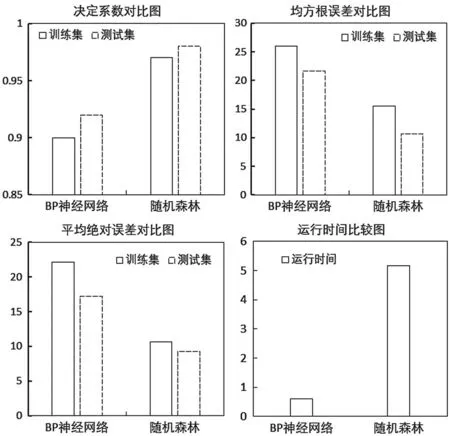
图4 BP神经网络和随机森林模型性能对比图

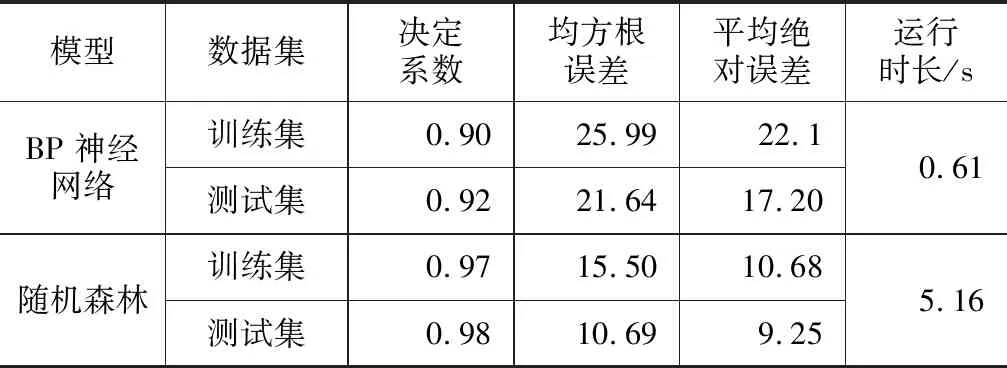
表2 预测模型预测性能评价表

由图4可见,从预测效果看,两种模型的决定系数均高于0.9,表示其预测性能均良好;其中,随机森林的预测性能明显优于BP神经网络,且测试集效果优于训练集;误差方面,随机森林模型的误差均小于BP神经网络模型的误差,且测试集误差小于训练集误差;但从运行时间长看,BP神经网络明显较短。两个模型预测效果随机森林明显优于BP神经网络,但BP神经网络模型的效率更高。

4 预测模型验证

为检验本文提出的两个模型,在镇江地区某项目中通过现场测试进行验证,该项目某钻孔的物理力学参数、标贯击数以及实测波速值如表3所示:

表3 地层指标参数

以表3的土层数据为验证样本,分别采用本文的两种模型和经验法式(1)对剪切波速值进行分析。所得的预测值(估算值)与实测值对比结果如表4和图5所示。

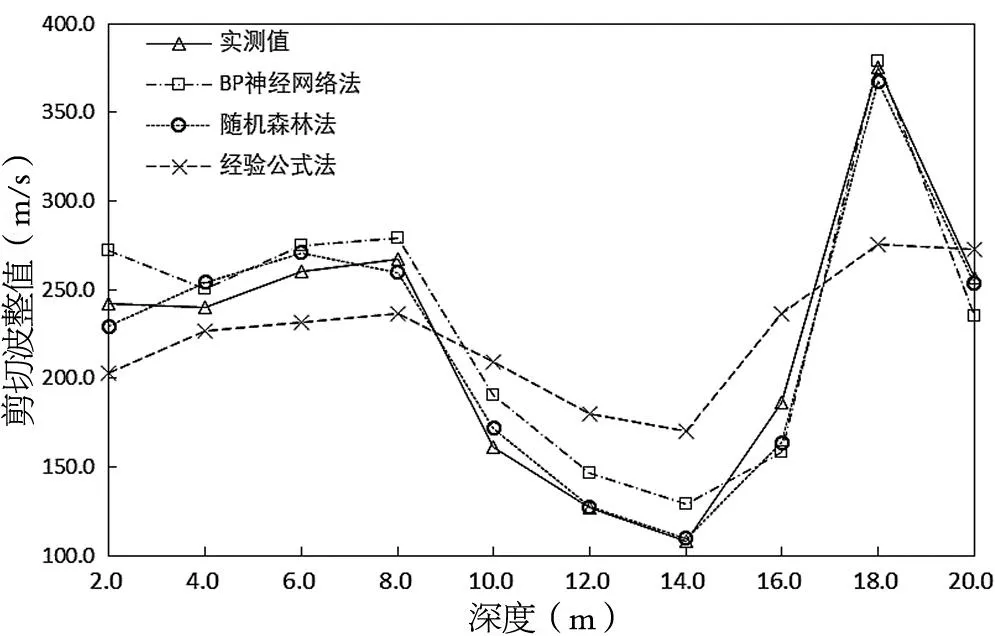
图5 预测结果对比

表4 预测值与实测值对比表

由表4可见,两种模型误差均低于20%,其中,随机森林预测模型的误差在0.5%～11.9%,BP神经网络模型的误差在1.0%～19.5%,经验法的误差在5.6%～57.6%。经验公式法因为其影响因素仅为标贯击数,而标贯击数并不能全面反映土层特性,尤其在土层性质变化较大或土质不均匀等情况下,故估算值只能大致反映土层波速值,由图5知经验公式法与实测法偏差较大,其中在偏软或偏硬的土层中误差最大。BP神经网络模型和随机森林模型带入了多种物理力学参数,几乎能全面反映各类土层的特性,由图5可知两种模型预测得到的剪切波速与实测值的趋势几乎一致;其中,随机森林法的准确性明显高于BP神经网络法,且随机森林法对偏软或偏硬的土层预测效果更优。

结果证明,两种预测模型均能够运用于实际工程的剪切波速预测,其中精度较高的随机森林模型更适合对实测剪切波速的验证。