重力差异导致的航天器设备安装精度变化量评估

李圣山，张少渤，石小兵

（航天东方红卫星有限公司，北京 100094）

0 引言

为保证航天器在轨姿态控制的准确性[1]，对于推力器、动量轮、红外地球敏感器、陀螺组件、星敏感器、数字太阳敏感器等具有安装精度要求的设备，其地面安装精度应最大程度地和在轨安装精度保持一致[2]。但由于地面与在轨环境间存在重力差异，使得在空间失重环境下原先的航天器设备安装精度发生变化[3]，会导致航天器的实际控制姿态与理论姿态间存在偏差。因此，分析天地环境重力差异对航天器设备安装精度的影响，对保证航天器在轨高精度姿态控制具有重要意义。

由于条件限制，航天器在轨设备安装精度无法直接测量，只能通过地面近似模拟获得。通过研究航天器设备安装精度在地面环境空载和满载状态下的变化规律，可近似反映在轨和地面环境间重力差异导致的航天器设备安装精度的变化规律。

目前，大部分对航天器设备安装精度的研究主要集中在精测工艺、精测方法、精测工具及测量算法上[4-9]。文献[3]给出了可以部分消除重力对设备安装精度影响的优化措施；文献[4]通过研究重力对载人航天器姿轨控敏感器等设备安装精度的影响，得出在空载、垂直停放状态下设备安装精度受地面重力影响较小。但迄今作者尚未发现有文献研究由于天地环境重力差异导致的设备安装精度的变化量分布规律。

本文通过对27 颗小卫星在地面空载和满载状态下的设备安装精度变化量进行统计分析，探寻航天器在空载和满载状态下设备安装精度变化量的分布规律，这对航天器在轨实际调整时进行偏差补偿、消除重力影响具有参考价值。

1 空载和满载状态下设备安装精度变化量统计

本文统计了航天东方红卫星有限公司2012 年至2018 年间发射的27 颗小卫星（单颗质量约600～1000 kg）的5 N 推力器、动量轮、红外地球敏感器、陀螺组件、星敏感器、数字太阳敏感器等设备的安装精度在地面空载与满载状态下的变化量，参见附录（其中变化量指同一设备同一坐标轴相对整星坐标系同一坐标轴之间的空间角度在空载及满载状态下的差值）。变化量的对数频率直方图如图1 所示，其中频率为各组样本数据的个数（称为频数）除以样本总个数所得的比值，lnV为变化量V的自然对数。

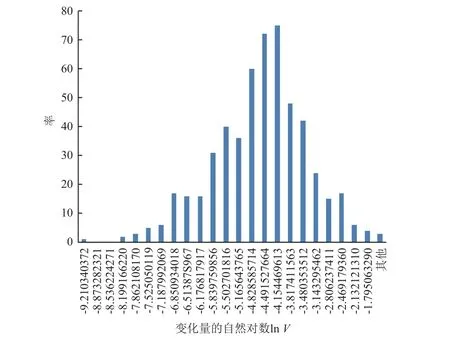
图1 航天器设备安装精度在空载和满载状态下的变化量的对数频率直方图Fig.1 Logarithmic frequency histogram for the variation in the installation precision of spacecraft equipment under both no-load and full-load conditions

2 结果与讨论

2.1 变化量分布类型的确定

分别用线性回归分析法和拟合优度检验法对第1 章所述变化量数据进行对数正态分布分析，以确定其分布类型。对数正态分布的概率密度函数为

其中：V为样本数据；σ表示样本的标准差；μ表示样本的均值。

2.1.1 线性回归分析

运用线性回归分析法需先对航天器设备安装精度在空载和满载状态下的变化量数据进行适当变换，再拟合为线性关系。记F(V)表示变化量的分布函数，Vi表示样本数据经过排序后的第i个样本，i=1, 2,···,n（n为样本数量，本研究中n=540）。Fˆ(Vi)为各样本中位秩，取为

Φ-1[F(V)]为标准正态分布积累分布函数的逆函数变换，

设y＝Φ-1[F(V)]=ax+b[10-11]，x＝lnV，得到线性回归方程

回归直线如图2 所示。利用相关系数法对得到的回归方程（式(4)）进行显著性检验，结果显示，对数正态分布模型的线性回归相关系数（r=0.993 3）远大于起码值（α=0.678 7），通过了检验。这说明对数正态分布可以表征航天器设备安装精度在空载和满载状态下的变化量分布规律。

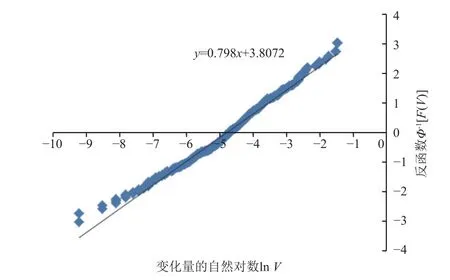
图2 航天器设备安装精度在空载和满载状态下的变化量的线性回归分析结果Fig.2 Results of linear regression analysis for the variation in the installation precision of spacecraft equipment under both no-load and full-load conditions

2.1.2 拟合优度检验

K-S 检验是一种常用的单样本正态性非参数检验方法，本文运用该方法对航天器设备安装精度在空载和满载状态下的变化量数据进行拟合优度检验，结果显示，在拟合优度α为0.01 时，对数正态分布的观察值（Dn=0.062 9）小于临界值（Dn,α=0.070 1），通过了检验。这说明用对数正态分布模型来描述航天器设备安装精度在空载和满载状态下的变化量分布是合适的。

2.2 变化量分布模型的参数估计

利用式(3)和式(4)，对对数正态分布模型的未知参数进行估计，得到参数 µˆ的估计值为-4.770 9，参数 σˆ的估计值为1.253 1。由对数正态分布模型的均值公式

计算得到服从对数正态分布时航天器设备安装精度在空载和满载状态下的变化量均值为0.018 6°（1′7″），与实测值0.016 8°（1′）间的最大相对误差为10.6%。这说明对数正态分布模型能较合理有效地表征航天器设备安装精度在空载和满载状态下的变化量分布。

3 结束语

本文运用统计分析方法，对航天器设备安装精度在空载和满载状态下的变化量进行研究，结果表明：对数正态分布模型预测的航天器设备安装精度在空载和满载状态下的变化量均值与实测值的相对误差最大为10.6%，说明用对数正态分布模型表征航天器设备安装精度在空载和满载状态下的变化量分布合理有效。有关结论间接揭示了在轨和地面环境间由于重力差异导致的航天器设备安装精度的变化量分布规律，对航天器在轨高精度姿态控制研究具有重要理论价值。