致密气藏压裂水平井产能影响因素分析

林利飞，王彦伟，李金阳，王恒力

（1.延长油田股份有限公司，陕西 延安 716099；2.延安大学 石油工程与环境工程学院，陕西 延安 716000）

苏里格气田已经成为中国年产气量最大的致密气藏，为保障中国经济发展和能源安全做出了巨大贡献［1-3］。压裂水平井大规模开发已经成为苏里格致密气藏高效开发的重要保障，因此探究苏里格致密气藏水平井产能影响因素对致密气藏开发具有重要意义［4］。

压裂水平井技术之所以能够使气井保持高效开发，主要因为通过压裂增大了裂缝的泄流面积，减小了流动阻力，同时使井筒周围的流动方式由径向流变为线性流，使地层压力下降更加缓慢，充分利用了地层能量［5-6］。压裂水平井在生产过程中，流动状态绝大多数时间处于不稳定流动阶段［7］。在其不同压力响应和产量递减的阶段，储层流体具有不同的流动形态，因而具有不同的压力和产量递减特征［8］。然而，由于致密气藏应力敏感性普遍较强，加之压裂后裂缝应力敏感性再次加强，导致应力敏感性对压裂水平井产能的影响不可忽略［9-11］。目前常采用油藏数值模拟技术、机器学习和数学模型的方法对压裂水平井产能进行评价［12-14］。但是，油藏数值模拟技术难以考虑应力敏感性因素的影响，而应力敏感性在致密气藏中普遍存在，因此油藏数值模拟技术分析误差较大［15］。机器学习技术则受到样本数量、机器学习方法的影响，其计算精度仍有待于提高［16］。数学模型方法的优点是可以根据各个气藏的特点针对性地考虑一些因素，例如滑脱效应、应力敏感、启动压力梯度等［17］。强贤宇等［18］考虑裂缝参数建立了强适用性的压裂水平井气-水同产产能预测模型，进一步完善了水平井产能评价体系。然而，针对苏里格致密气藏储层特征的水平井产能影响主控因素仍然模糊，尤其是产能影响因素的敏感性研究报道极少。

针对以上亟需解决的实际问题，本研究充分考虑气-水两相渗流在地层和裂缝中不同渗流规律及裂缝间相互干扰，基于致密储层渗流理论，建立压裂水平井各个流动阶段的数学模型，获得各流动阶段井底压力的解析解，在此基础上，利用杜哈美原理，将产量与压力进行转换，得到产量递减曲线。重点分析裂缝数量、裂缝长度、裂缝导流能力以及应力敏感等因素对水平井产能的影响。该研究有助于解决目前苏里格气田压裂水平井开发的实际问题，指导开发人员准确把握气井生产动态。

1 数学模型的建立

根据实际区块的地质条件，假定在均质气藏中心有口压裂水平井，模型的边界条件为封闭圆形，裂缝方向为垂直横向，如图1所示。水平段方向为y轴方向，裂缝面与水平段方向垂直。模型假设水平井压裂缝为有限导流，每条横切水平井的裂缝具有相同属性，即裂缝的长度、宽度、高度和导流能力都保持一致，流体通过裂缝流入水平井筒，且总流量保持不变。流体在储层内的流动主要有基质到裂缝的流动、裂缝内的流动、裂缝向井筒内的流动。由于其储层为致密砂岩，没有压裂就没有产能，所以忽略由基质向井筒内的流动。

图1 压裂水平井物理模型图

在圆形封闭气藏内的压裂水平生产井模型中，其地层及流体满足：1）气藏顶底和圆形边界均为不渗透边界；2）气体的渗流过程符合达西定律，不考虑毛管力和重力的影响；3）假定裂缝半长为Lf，其方向与井筒方向垂直，完全穿透储层。

对于压裂水平井的多裂缝间相互干扰问题，AMINI 等［19］采用数值离散的方法来描述裂缝之间的干扰流动，但这种方法比较复杂，而且中期径向流动特征描述不是很明确。本文利用叠加原理表征裂缝干扰的影响。若水平井包含n条裂缝，考虑整个系统时，每条裂缝看作一个单元，那么将有n+1 个未知量，由点源解沿裂缝方向进行积分，得到线源解，将各影响函数进行叠加，解决了裂缝之间的干扰问题，同时引入裂缝导流能力影响函数，给出有限裂缝导流能力压裂水平井产量动态分析。

根据物质平衡方程、状态方程和达西定律建立偏微分方程。在均质地层中其连续性方程为

真实气体定律：pM=ZgρRT。

根据Warren 和root 理论，由于致密气藏的渗透率比较小，认为在基质中流动为拟稳态流动［20］，则式（1）可转换为

其中，L和Lf分别为水平段长度和裂缝半长，m；h为储层厚度，m；μ和μi分别为气体黏度和原始地层条件下气体黏度，mPa·s；ϕ为孔隙度；Ct和Cgi分别为综合性压缩系数和原始地层条件下气体等温压缩系数，MPa-1；γ为应力敏感系数；ppi和pp分别为原始和目前地层压力，MPa。

将式（3）和（4）代入式（2）中，渗流方程可转化为

由于渗流方程的非线性，难以求解，因此为了将方程线性化，对渗流方程进行Pedrosa 代换。式（5）符合贝塞尔方程的条件，因此方程通解为

再根据其边界条件得到

其中，reD为无因次供给半径。

对裂缝面上某点处压力解沿裂缝方向进行积分，则式（6）变为

其中，K1(x)、I1(x)称为第二类变形函数K0(x)、I0(x)的一次积分，S为裂缝导流能力。

贝塞尔函数的比值tS在初期几乎为零，但在后期对贝塞尔变形函数积分很难取得精确值，因此，对式（7）的右边采用Ozkan 给出单条裂缝井在封闭气藏中产生的压力降：降落，所以在地层中任意一点产生的压力降都等于各条裂缝产生的压力降之和。第i条裂缝处的压力为

再经过转换

由于压裂水平井的产量为各条裂缝产量之和，然后对其进行拉普拉斯变换即可得到

其中，xeD为供给边界与x方向的无因次距离，xwD为井筒边界与x方向的无因次距离；ywD为井筒边界与y方向的无因次距离；I为水平井的无因次累积生产时间为井筒内流动产生的无因次压力降；为裂缝产生的无因次压力降总和为基质内流动产生的无因次压力降为裂缝内流动产生的无因次压力降，因值较小，计算忽略为基质向裂缝流动产生的无因次压力降。压裂水平井沿井筒方向压裂产生n条裂缝，在生产过程中，每条裂缝都会有地层中的气体向其流动，造成压力

因为是无限导流，所以每条裂缝处的无因次压力相等，所以

因此式（15）和（16）中有n+1 个变量和n+1 个方程，所以建立方程矩阵为

如果考虑到裂缝为有限导流能力，那么裂缝内存在压力降，对于封闭油藏压裂水平井有限导流裂缝压力分布建立起来的矩阵方程对角线上的元素发生变化：

根据杜哈美原理无因次压力和无因次产量的拉普拉斯空间下的转换关系为

则根据stephest 反演即可解得无因次压力和无因次产量。

2 压裂水平井的渗流特征分析

利用式（20），经过stehfest反演计算封闭边界气藏压裂水平井的井底压力公式，对该公式进行编程计算，可绘制封闭气藏压裂水平井的压力动态曲线，如图2 所示。根据无因次压力一阶导数曲线形态划分，可将压裂水平井流动阶段划分为5段：早期线性流（Ⅰ）、中期径向流（Ⅱ）、中期线性流（Ⅲ）、系统径向流（Ⅳ）和边界控制流（Ⅴ）。在早期线性流阶段，曲线主要反映2个线性流动同时发生，即流体从人工裂缝流向井筒和流体从储层流向人工裂缝，该阶段的压力及压力导数曲线的形态是斜率为1/4的直线；在中期径向流阶段曲线主要反映流体从储层到人工裂缝的流动；在中期线性流阶段曲线主要反映流体从储层到人工裂缝的椭圆流动；系统径向流阶段，曲线主要反映后期流体从储层到人工裂缝的径向流动，该阶段的无因次压力导数曲线为近似水平直线；边界控制流阶段，压力波探测到了封闭外边界，流体开始进行拟稳定流动，其压力和压力导数曲线为斜率为1的直线。

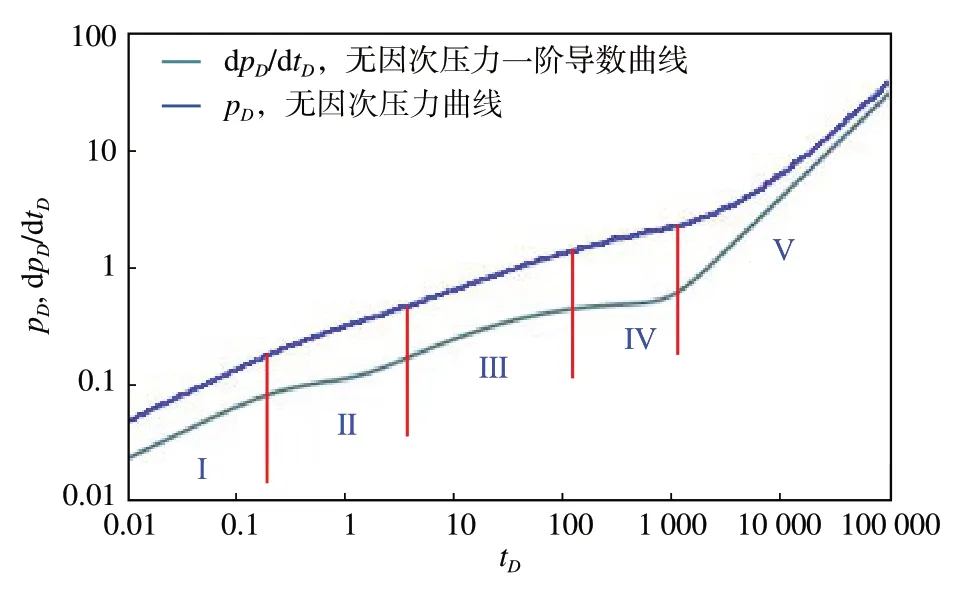
图2 压裂水平井的无因次压力曲线

同时应用杜哈美原理，根据式（20）经过stehfest 反演，应用Blasingame 方法计算得无因次产量的递减曲线如图3 所示，可知图包括两部分曲线，前半部分是非稳态流动的曲线特征，后半部分是边界控制流的曲线特征。与水平井Blasingame的典型曲线图对比，可知压裂水平井的产量更高，尤其是在边界控制流动阶段，产能差异更大。因此如果压裂水平井的生产数据直接采用典型水平井曲线来拟合、计算，将会对压裂水平井产量造成很大的偏差。

图3 压裂水平井的无因次产量递减曲线

3 影响因素分析

3.1 裂缝数量的影响

在无因次供给半径reD=40，裂缝半长Lf=80 m，裂缝间距LD=200 m，无应力敏感和无限导流能力下，绘制不同裂缝数量时压力变化动态曲线和无因次产量递减曲线，如图4 所示。由压力动态曲线（图4A）可知，随着裂缝数量增多，近井地带储层改造效果变好，在短时间内储层中大量的天然气从基质渗流至裂缝中并被采出，表现为开发初期井底压力降低的幅度增大。对比发现裂缝数量越多，裂缝之间的线性流和径向流时间越长。由产量递减曲线（图4B）可知，随着裂缝数量的增多，水平井初期的产量增加，但是产量递减也加快。因此水平井裂缝数增多，可以有效的提高水平井初期产量。

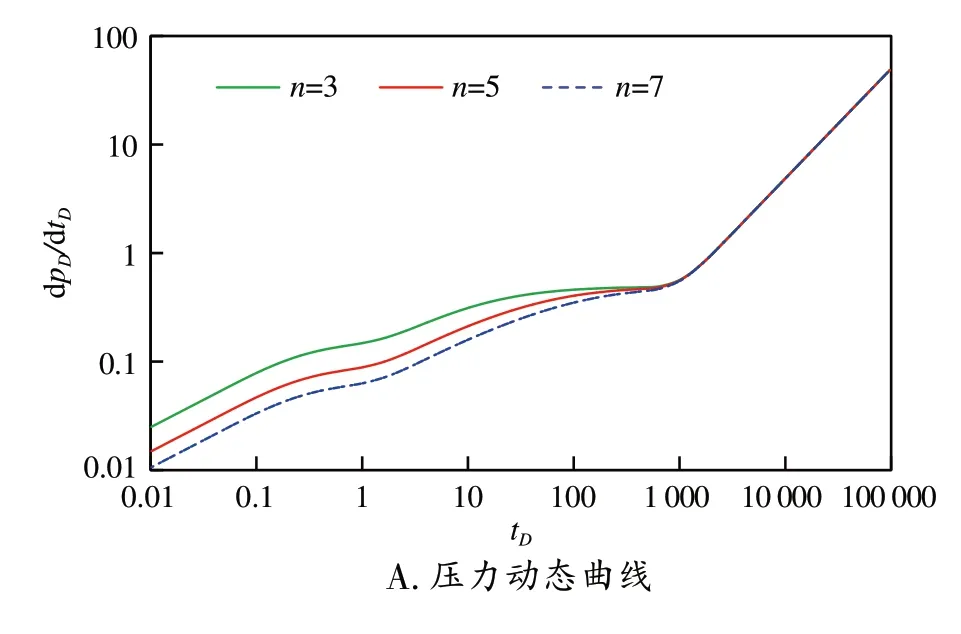
图4 裂缝数量对压力和产量动态曲线的影响

3.2 裂缝半长的影响

在无因次供给半径reD=40，裂缝数n=5，裂缝间距LD=200 m，无应力敏感和无限导流能力下，绘制不同裂缝半长时压力动态曲线和无因次产量递减曲线，如图5 所示。由图5A 可知，在不同的裂缝半长下，早期线性流阶段压降速率线几乎重合，表明裂缝半长对早期线性流没有影响。其原因在于早期线性流阶的渗流过程为流体从人工裂缝流向井筒和从储层流向人工裂缝，裂缝半长的大小并不能影响流体早期渗流的速率，因此裂缝半长对早期线性流没有影响。裂缝半长主要影响中期线性流、系统径向流和边界控制流阶段，裂缝半长越大，中期线性流持续时间越长，中期径向流越短，压降也越大。在中期线性流至边界控制流阶段，流体分别经过了从储层到人工裂缝的椭圆流动、从储层到人工裂缝的径向流动、拟稳定流动状态，此时裂缝半长越大则参与渗流的基质范围越广，因此压降速率越大。图5B 表明，随着裂缝半长的增大，开发早期水平井产量增大，同时递减率也增加。在进入开发后期，不同裂缝半长的产量曲线重叠，表明在开发后期裂缝半长对产量的影响逐渐减小。因此，相同条件下水平井的初期产量随着裂缝半长的增大而增大。

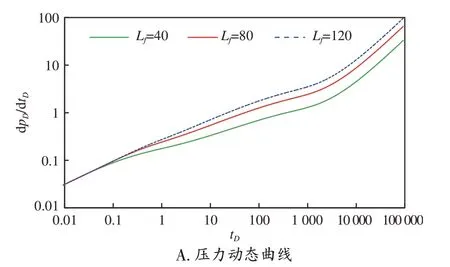
图5 裂缝半长对压力和产量动态曲线的影响

3.3 导流能力的影响

在无因次供给半径reD=40，裂缝数n=5，裂缝半长Lf=80 m，裂缝间距LD=200 m，无应力敏感下，绘制不同导流能力时的压力动态曲线和无因次产量递减曲线，如图6 所示。由图6A 可知，裂缝导流能力主要影响早期裂缝线性流和径向流，在该阶段，裂缝导流能力越大，压力降落速率越快，在其他渗流阶段压力降落曲线重合，表明裂缝导流能力对中期线性流、系统径向流和边界控制流阶段几乎无影响。图6B表明，在水平井开发早期，裂缝导流能力越大，早期产量越大，开发后期对产量的影响逐渐减弱。其主要原因：在开发早期气体从人工裂缝流向井筒和流体从储层流向人工裂缝，因此裂缝的导流能力至关重要，导流能力越大则早期产能越大；在开发中后期，主要的渗流特征为气体从储层到人工裂缝的径向流动，该阶段以基质孔喉内的渗流为主，加之开发后期地层压力下降引起人工裂缝闭合，因此裂缝导流能力的大小在该阶段对产能影响较弱。

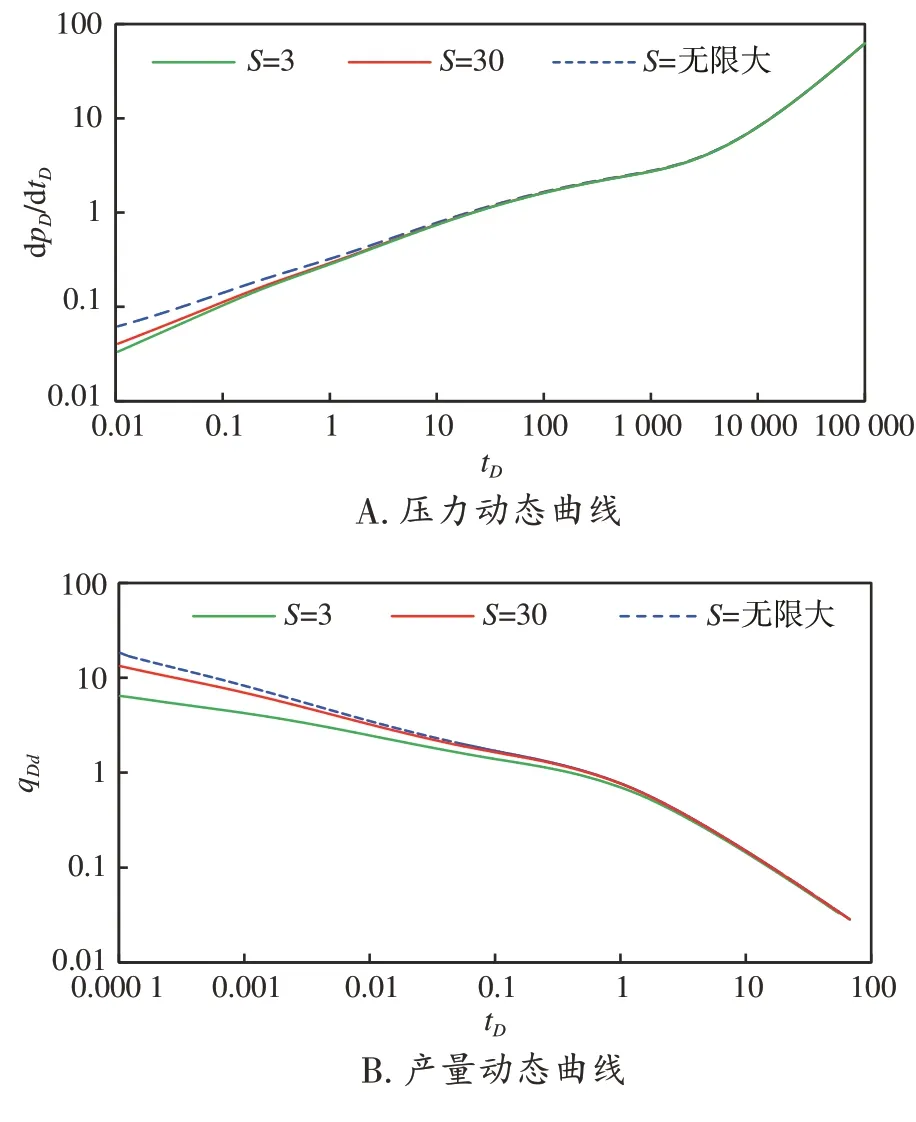
图6 裂缝导流能力对压力和产量动态曲线的影响

3.4 应力敏感的影响

为确定应力敏感系数的取值，选取苏里格气田苏54 区盒8 段致密储层的样品进行了应力敏感性实验。实验过程：将岩心在104 ℃下干燥10 h，将干燥后的岩心放入岩心夹持器中，并将围压增加到2 MPa，驱替压力为0.2 MPa，出口端压力为大气压，记录固定时间（60 s）出口处的气体体积，当连续3 次测量的误差小于2%时则认为达到稳定渗流状态，停止计量。随后将围压提高1 MPa，待稳定后再次测量出口端气体体积。根据测量得到的压力、时间、气体体积等参数计算岩心渗透率，当围压为25 MPa时，渗透率不再减小，结束实验。实验最终得到了岩心在不同围压条件下的渗透率。应力敏感系数计算公式如下：

其中，K0为初始渗透率，mD；∆K为渗透率变化量，mD；∆P为压力变化量，Mpa。

图7为实验所得到的相对渗透率和应力敏感系数与围压的关系曲线图，相对渗透率为样品目前的渗透率与初始渗透率之比。由7A 图可知，岩心样品的相对渗透率随着围压的增加而降低，根据渗透率变化率将围压加载过程分为3 个阶段，围压由2 MPa增加至5 MPa时相对渗透率减小至0.63，在这个阶段相对渗透率的损失率为37%，相对渗透率随着围压的增加而迅速减小；围压由5 MPa 增加至15 MPa时，相对渗透率由0.63 减小至0.25，相对渗透率的损失率比前一阶段小，但对致密气藏开发的影响仍不可忽视；围压由15 MPa 增加至25 MPa 时，相对渗透率减小至0.15，意味着围压为25 MPa 时渗透率仅为初始渗透率的15%，在这个阶段相对渗透率的变化率最小。由图7B 可知，致密气藏应力敏感系数随围压增加而不断减小，其分布范围为0.015～0.077，因此本研究应力敏感系数取值为0、0.06、0.08。

图7 相对渗透率和应力敏感系数与围压的关系曲线图

在无因次供给半径reD=40，裂缝数n=5，裂缝间距LD=20，裂缝半长Lf=80，无限导流能力下，绘制不同应力敏感系数时的压力动态曲线和无因次产量递减曲线，如图8 所示。由图8A 可知，应力敏感主要影响地层边界控制流，应力敏感越强，其拟压力及其导数越往上翘，边界流时间也越短；在线性流和系统径向流时期影响比较小。图8B表明，在曲线形态上的拟稳态阶段，产量下降幅度最大，产量递减曲线不再遵循调和递减，导致可动用储量减小。主要是因为在拟稳态阶段地层压力下降幅度较大，在该阶段应力敏感系数较大，储层渗透率大幅度下降，引起产能下降，结果表明应力敏感越强，对产量的影响越大。

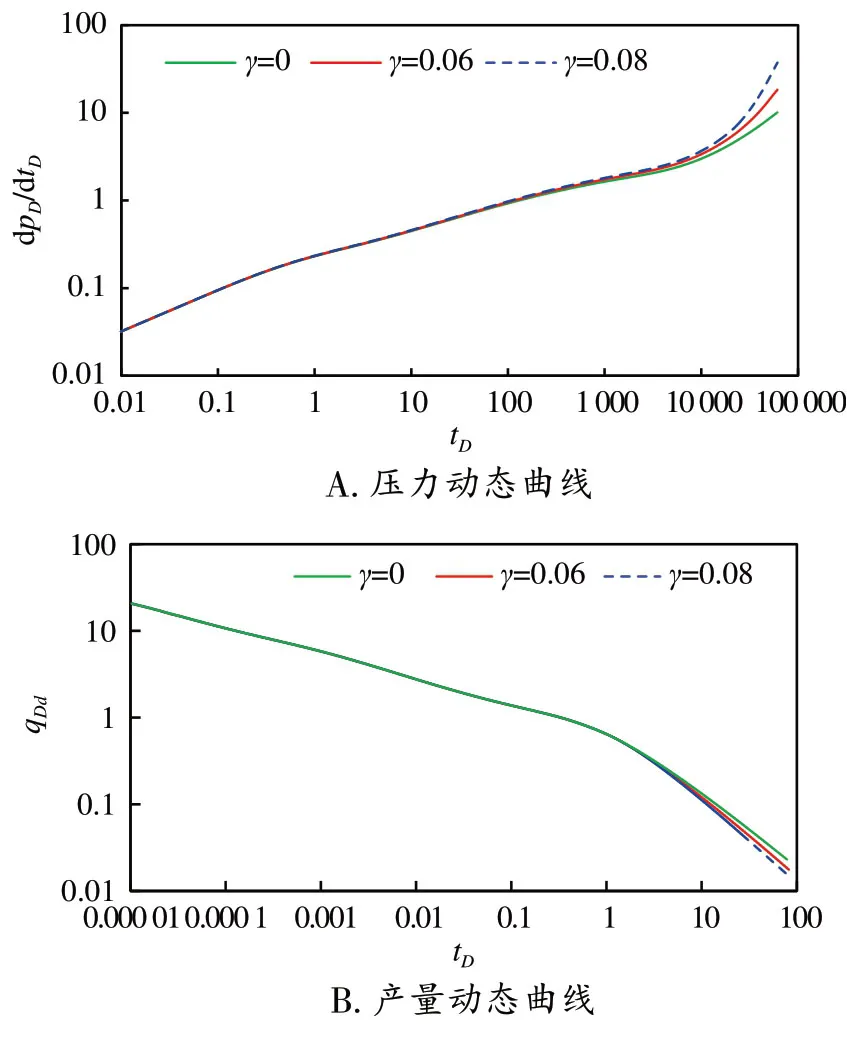
图8 应力敏感对压力和产量动态曲线的影响

4 主控因素分析

本文以苏里格气田苏54 区盒8 段储层为例，分析致密气藏压裂水平井产能影响的主控因素。苏54 区主要岩石类型为石英砂岩、岩屑石英砂岩和岩屑砂岩，其中石英砂岩含量最大，可达到52.2%，岩屑石英砂岩含量次之，可达到39.6%。碎屑成分以石英类为主，岩屑类次之。填隙物以伊利石、高岭石、硅质居多。目标储层主要以粗砂中-粗粒（43.9%）、中粒（38.5%）为主。研究区目标层位孔隙度分布范围为4.5%～11.3%，平均孔隙度为8.8%；渗透率介于0.12～3.85 mD，平均为0.36 mD；平均含气饱和度为54.3%，储层厚度为6.5 m。根据以上储层物性特征判断，研究区属于典型的致密气藏。研究区目标层位水体不发育，开发过程几乎不产水。

分别求取裂缝数量、裂缝半长、裂缝导流能力、应力敏感系数对水平井初期产量、累积产量的相关系数，进而根据相关系数确定水平井产量的主控因素。分别根据图4B、图5B、图6B 和图8B 获得不同影响因素下的无因次产量，结果如表1所示。

表1 不同影响因素下的无因次产量

根据式（21）计算各个因素与无因次产量的相关系数，结果如表2 所示。无因次初期产量相关性最强的是裂缝数量，其相关系数达到2.35，相关性最弱的是导流能力，相关系数仅有0.22。无因次累积产量的相关性由强到弱顺序为裂缝数量>裂缝半长>应力敏感>导流能力。因此对于致密气藏水平井开发，在经济效益允许的范围内，应该增加裂缝数量、增大裂缝半长。

表2 影响因素的相关系数计算结果表

其中，R为相关系数；ΔqDd为无因次产量的变化量；a1、a2分别为影响因素的无因次特征值。

5 结论

1）有限导流裂缝压裂水平井的曲线形态主要为线性流和径向流，导数曲线形态可划分5个阶段：早期线形流、中期径向流、中期线性流、系统径向流和边界控制流。

2）裂缝数量增加，水平井开发初期产量增加，但是递减也加快；裂缝半长主要影响中期线性流、系统径向流和边界控制流阶段，裂缝半长越大，开发初期单井产量越大；在水平井开发早期，裂缝导流能力越大，早期产量越大，开发后期对产量的影响逐渐减弱；应力敏感主要影响地层边界控制流，在水平井开发后期，应力敏感越强，产量下降幅度越大。

3）影响致密气藏压裂水平井渗流的影响因素按作用大小排序为裂缝数量>裂缝半长>应力敏感>导流能力。因此在致密气藏水平井开发过程中，可通过增加裂缝数量和增大裂缝半长来提高水平井产量。