局部超挖对内支撑结构的施工效应

2024-01-08魏焕卫李传斌种记鑫郑晓

计算机辅助工程 2023年4期

魏焕卫, 李传斌, 种记鑫, 郑晓

(1. 山东建筑大学 a. 土木工程学院; b. 建筑结构加固改造与地下空间工程教育部重点实验室;c. 地铁保护研究所, 济南 250101; 2. 济南轨道交通集团有限公司, 济南 250100)

0 引言

局部超挖可定义为在未架设某层支撑时,分层开挖至该层内支撑设计位置并继续向下开挖一段深度,然后再进行架设支撑[1]。在基坑的施工过程中,由于设计不妥、工期紧张或地质条件等原因,局部超挖时常发生。一方面,局部超挖区长度和深度越大,越有利于施工且缩短工期;另一方面,局部超挖过度可能会引起结构变形、超限失稳等问题。如何控制局部超挖的量以及由其引起的施工效应,是一个亟待解决的问题。此外,支撑架设不及时导致局部超挖也引发大量的基坑事故[2-6],造成严重损失。

目前,已有许多学者对基坑的局部超挖进行了相关研究。张瑾[7]统计114例上海地铁基坑险情,其中50%与局部超挖有关。王峰等[8]采用层次分析法确定超挖和支撑及时架设程度的风险等级水平,明确超挖对施工开挖影响巨大,应严格控制。罗阳洋[9]建立有限元模型,系统研究基坑超挖深度、超挖范围及超挖位置对围护结构水平变形的影响。谢秀栋等[10]研究土体蠕变特性。张广达[1]、黄珠微[11]通过数值模拟,探讨超挖深度对围护结构地表沉降的影响规律。黄天明等[12]以悬臂排桩支护的长条形基坑为例,研究基坑局部超挖深度对支护桩弯矩、侧移的传递机理。雷亚伟等[13]结合模型试验,引入弯矩增大系数,对基坑局部超挖引起的载荷传递规律进行探索。郑刚等[14]进一步研究局部超挖对双排桩内力、变形及稳定性的影响,提出判断倾覆型连续破坏发生和发展范围的抗倾覆稳定状态值方法。孙威等[15]提出考虑结构相互作用的三维杆系有限元分析方法,考虑局部土方超挖的因素对支护结构变形及受力的影响。

现有对基坑局部超挖的研究大多集中在超挖安全性分析及险情处理或对围护结构内力及变形[16-19]的影响上,研究对象为悬臂或单支撑围护结构,而对内支撑结构中的局部超挖施工效应以及影响范围的研究较少。本文利用PLAXIS 3D软件建立三维数值模型,研究分析基坑内不同支撑条件下超挖深度及宽度对支护结构的施工效应,包括支护结构内力位移及桩后土压力的影响,提出局部超挖施工效应影响系数ki、li、mi、ni,以评估局部超挖施工效应影响范围,以及确定侧移弯矩控制值的方法,为实际工程提供参考。

1 工程实例分析

1.1 工程概况

对某深基坑工程,取存在挖深差的剖面部分进行分析。基坑平面形状及监测点位置见图1(a),东西长约125 m,南北长约48 m,本文主要对基坑典型局部超挖区域的监测数据进行分析。

(a)基坑平面形状及监测点位置

基坑采用支护桩与钢筋混凝土对撑、角撑支护,Ⅰ区域混凝土对撑与立柱共同支护,Ⅱ区域混凝土角撑处与立柱共同支护。Ⅰ区域开挖深度为14.4 m,竖向布置2道支撑;Ⅱ区域开挖深度为22.0 m,竖向布置4道支撑;Ⅲ区域开挖深度为21.4～14.0 m,放坡开挖,竖向布置3道支撑,有限元模型见图1(b)。

由地勘报告可知,土层按一般工程地质性质差异自上而下共分为7层,其物理力学性质指标见表1。本文主要分析Ⅱ、Ⅲ区域基坑围护结构变形内力,Ⅱ区域为局部超挖区,Ⅲ区域为放坡区域,主要施工工况信息见表2。工况3时Ⅰ区域已至坑底,工况4、5中存在局部超挖。

1.2 模拟及实测数据分析

模拟部分利用PLAXIS 3D三维有限元软件进行,土体支护形式和开挖工况与实际工程相同,模型选取土体硬化(H-S)模型,能够较好地模拟基坑的开挖过程[20]。各侧移和内力测点位置见图1(a),根据工程施工过程中不同时期的监测数据,对比深层水平位移观测点处5～10冠梁的水平位移,桩体向坑内变形为正,实测数据及模拟结果对比见图2。

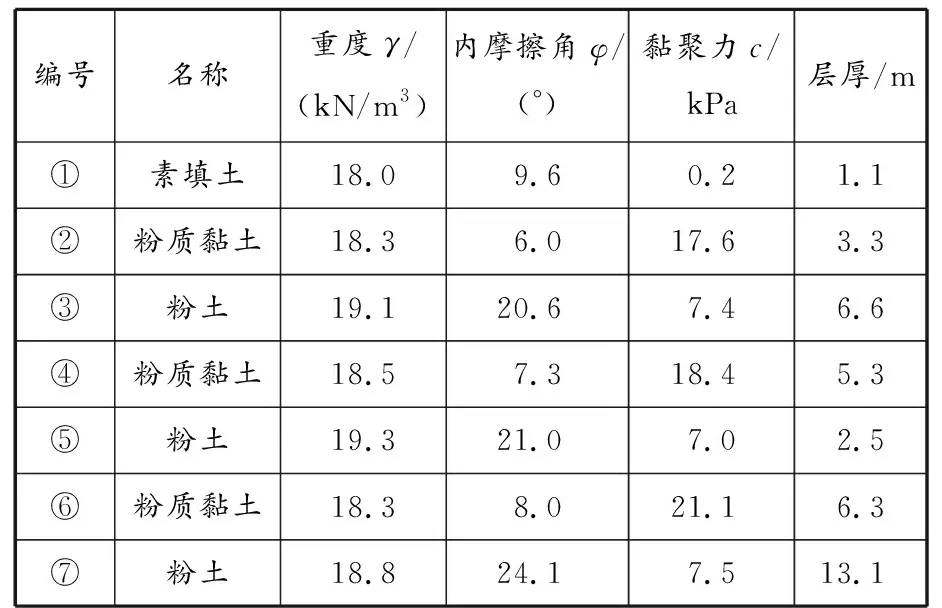
表 1 土层物理力学性质指标

表 2 施工工况

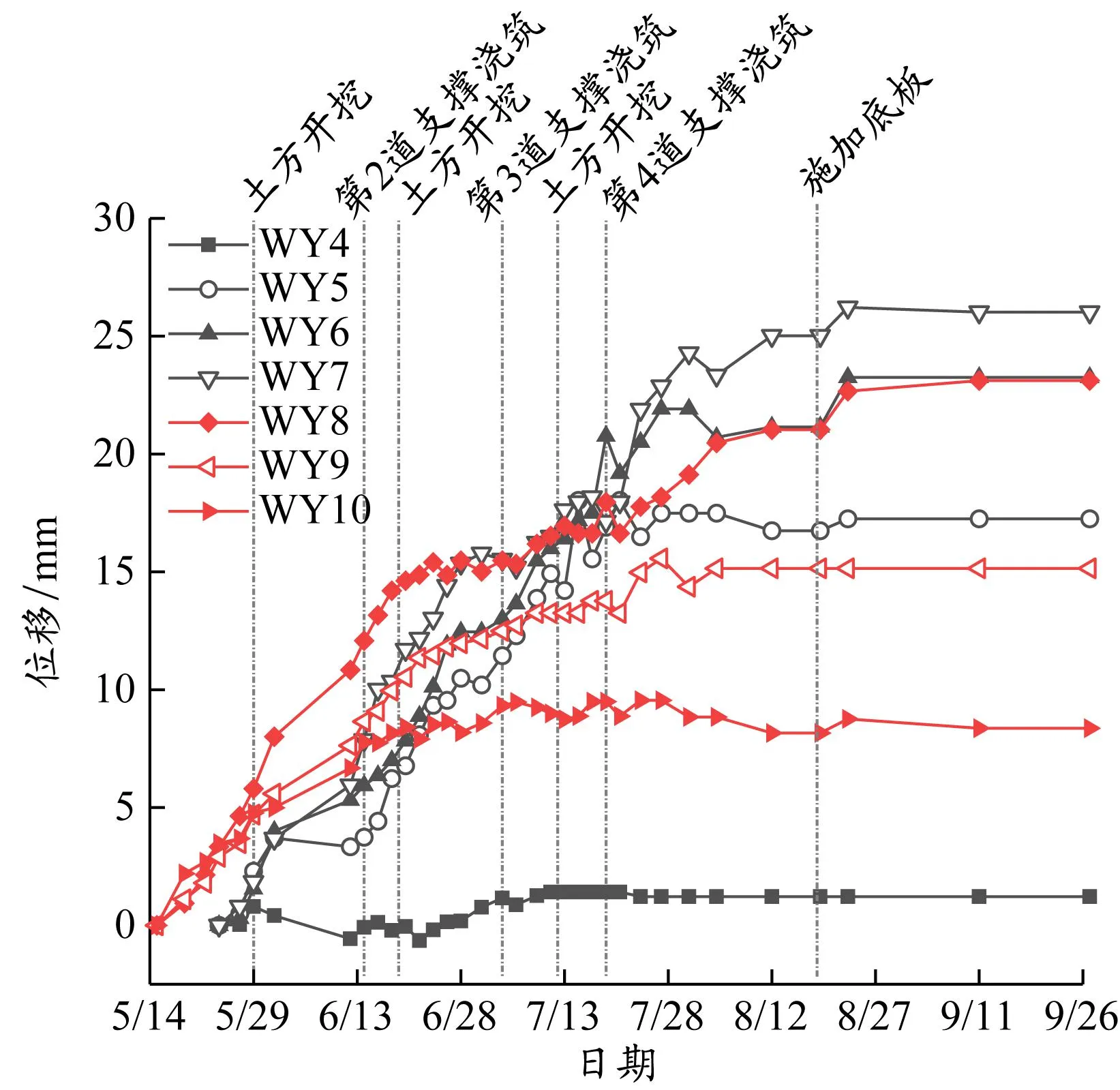
(a)实测数据

从冠梁实测数据可知,随着开挖深度的增加,各测点处冠梁水平位移向坑内有逐渐增大的趋势。测点WY4～WY7在Ⅱ区域有超挖,中心测点WY7比远离超挖中心的WY5、WY9测点分别超挖增加50%和72%,变化较大;随着远离超挖区,冠梁水平位移逐渐减小。在超挖区内,有限元模拟与实测数据最大值相差16%,结果虽然有差异,但数值比较接近且变化趋势一致。

轴力监测以及模拟数据见图3,受施工工况的影响,各测点的轴力值均呈波动变化。轴力测点ZL5位于超挖中心,该测点除第1道支撑轴力小于其他测点外,第2道和第3道支撑均大于其他测点,实测数据中第2道支撑轴力测点ZL5达到轴力测点ZL6的1.94倍。

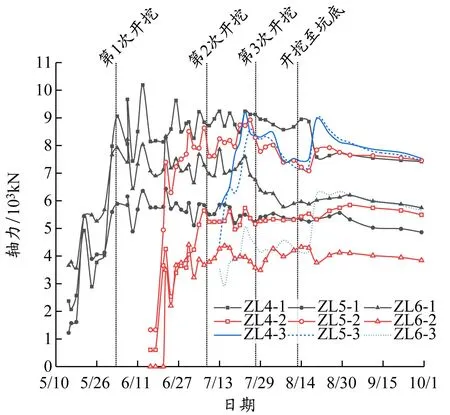
(a)实测数据

各工况下测点ZL5和ZL6轴力与ZL4的轴力比(各测点轴力与ZL4测点轴力的比值)见图3(b),可知数值模拟具有较好的一致性。因此,超挖对邻近区域侧移和内力有明显影响,在实际工程中应特别注意局部超挖引起的轴力变化。

2 有限元模型的建立

2.1 模型及计算参数

为研究局部超挖施工对围护结构的变形影响,利用上文方法建立某个长条式基坑模型进行分析。最大开挖深度He为15 m,基坑开挖影响范围通常为3～4倍基坑挖深[21],基坑平面尺寸为75 m×5 m,因此确定模型尺寸为170 m ×100 m×60 m,以消除边界条件的影响。模型为对称结构,对称面为yz面,在分析中仅取x>0部分,见图4。

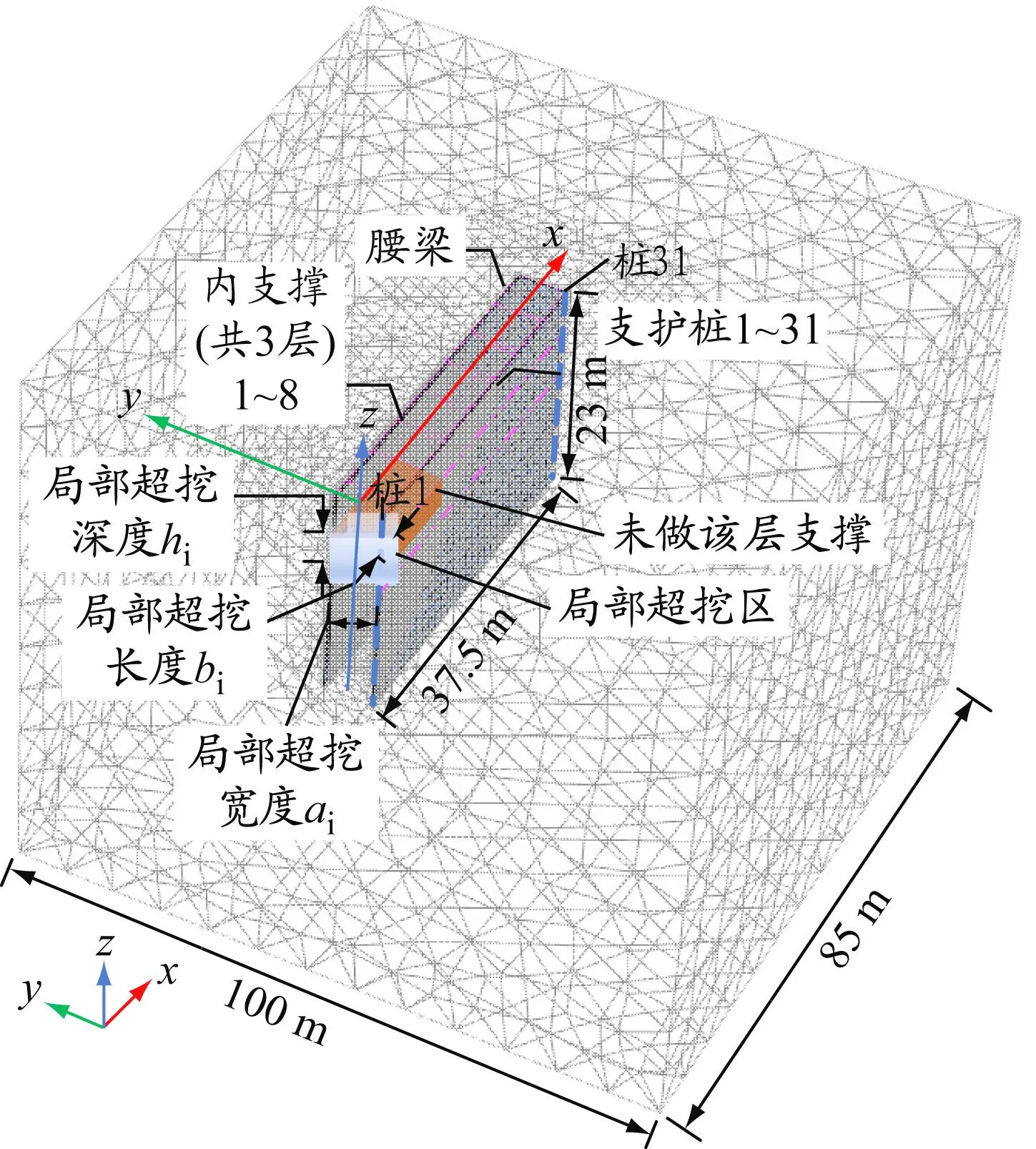
图4 基坑有限元模型及分析网格

采用排桩内支撑支护结构,桩径600 mm,净距650 mm,桩长23 m。根据等刚度[22]原则,将支护桩等效为板进行数值模拟,板厚d=0.39 m,弹性模量E=30 GPa。其余支护结构内支撑、腰梁、冠梁采用梁单元模拟,自地面标高处设置冠梁与支撑,往下每隔5 m设置1道腰梁与支撑,支撑水平间距为5 m,统一取截面600 mm×600 m。模型取单一均质土层,同样取土体硬化(H-S)模型,土体力学参数见表3。综合考虑计算速度和精度,对基坑及附近进行局部网格加密。

2.2 模拟方法

图5为全结构局部超挖示意,仅取x>0部分进行分析。基坑宽度a=5 m,固定局部超挖区长度B=2b=5和15 m为例,改变局部超挖深度hi=0.5i(i=1,2,…,10 m)。按此方法将模型分为:(1)算例1,无支撑局部超挖,见图5(a);(2)算例2,有1道支撑的局部超挖,见图5(b);(3)算例3,有2道支撑的局部超挖;(4)算例4,正常支撑条件下分层整体开挖。

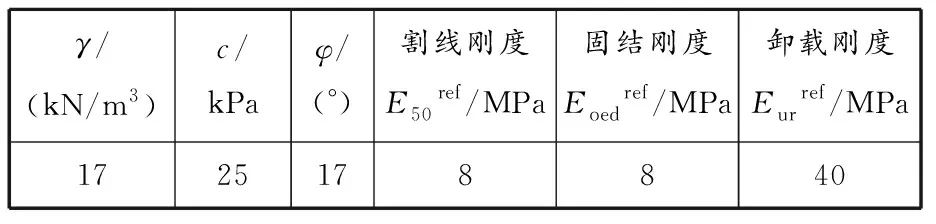
表 3 土层力学参数

(a)无支撑局部超挖

2.3 施工效应初始值及系数的定义

将算例4中分层整体开挖5 m后的支护桩最大侧移作为侧移初始参考值,此时算例4与其他各算例中局部超挖深度hi=5 m时的坑底深度相同。同理,将算例4开挖至局部超挖相同坑底深度时的桩身最大弯矩,称为弯矩初始参考值,用于结合规范参考值对局部超挖进行控制。

为研究局部超挖对支护结构的影响程度和范围,引入施工效应系数ki、li、mi、ni。

(1)

(2)

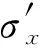
3 无支撑局部超挖

3.1 无支撑局部超挖下支护桩侧移

算例1为无支撑局部超挖,超挖时支护桩桩身最大侧移及侧移变化系数曲线见图6,支护桩向坑内位移为正。

(a)侧移曲线

如图6(a)所示,支护桩侧移随局部超挖深度和长度的增加而有显著增长趋势,因空间效应,超挖长度增加、未开挖土体减少,抗力变小对支护桩侧移的限制作用减小。沿基坑长度方向上,在局部超挖范围内,支护桩向坑内侧移及变化速率最大,随着与超挖区距离增大,侧移逐渐减小并趋于稳定,在距坑角1.5倍开挖宽度范围内,因坑角效应侧移迅速减小。

在算例1中,侧移初始参考值为5.87 mm。在局部超挖区长度B=5和15 m,局部超挖深度hi分别为3.5、2.5 m时,支护桩侧移已接近侧移初始参考值。局部超挖深度hi=5 m,B=5和15 m时,支护桩侧移分别为8.72、23 mm,位移增量是初始侧移参考值的49%和291%。若基坑为一级基坑,根据规范[23],水平位移允许值取10 mm,故超挖区长度若达到15 m,则支护体系将存在位移超限的风险。

根据式(1),超挖区长度B=5和15 m时,各超挖工况下各位置处的支护桩最大侧移变化系数ki见图6(b)。定义ki稳定在0.9～1.1时,为局部超挖影响范围之外;反之,则为影响范围之内。对于算例1的无支撑下局部超挖,沿基坑长度方向上侧移变化系数逐渐减小,当侧移变化系数ki稳定小于1.1,则认为不受局部超挖影响。

3.2 无支撑局部超挖下的桩后土压力

算例1的无支撑下局部超挖,取局部超挖时坑底以下2 m支护桩后土压力和未开挖之前的桩后土压力,研究局部超挖深度及其变化对土压力的影响以及在沿基坑长度方向上的传递规律。

算例1的土压力变化系数见图7。相对于局部超挖前,局部超挖范围内及附近区域桩后土压力呈减小趋势,邻近区域桩后土压力呈增长趋势,桩后土压力增长速率随着与局部超挖区距离的增大而减小,超过一定区域后则基本与局部超挖前相等。局部开挖范围及其邻近区域桩后土压力增减程度和影响范围随局部超挖深度和长度的增加而变大。因测点均为局部超挖面以下,局部超挖区内土体开挖卸荷,支护桩向坑内发生较大水平位移,使得超挖区桩后主动区土压力迅速减小,而非超挖区支护桩水平变形较小。这种位移差异使得桩后土体形成水平土拱[24-25],超挖区水平载荷被转移至非超挖区,对支护桩产生加载效应[26],桩后土压力弯矩均有所增加,但此时土压力增幅不大。li在局部超挖区内最小,随着远离开挖中心先逐渐增大至最大值,随后减小并趋于稳定,此时若li在0.99～1.01,则认为此时超出局部超挖对桩后土压力的影响范围。

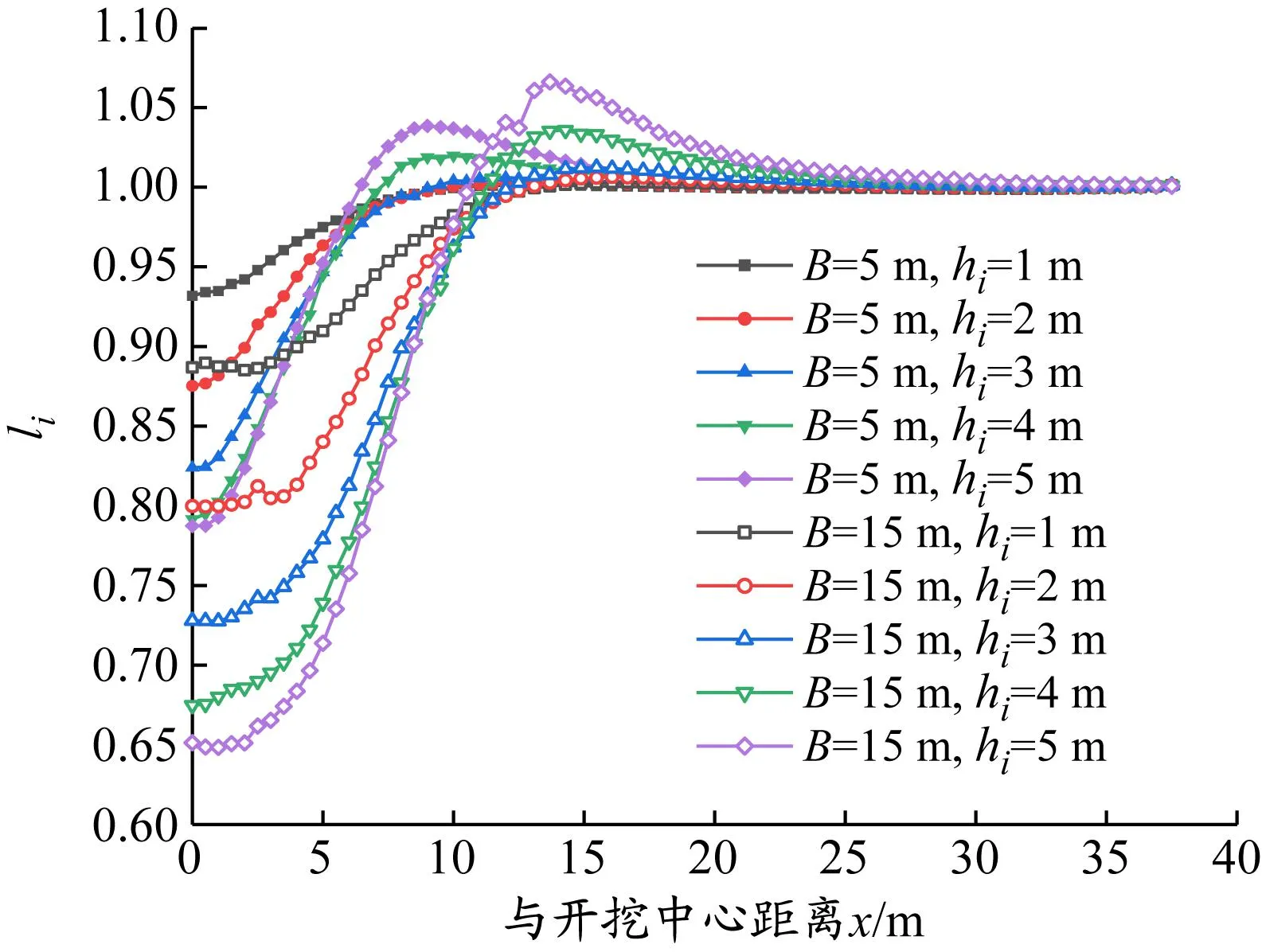
图7 算例1土压力变化系数

3.3 支护桩弯矩

算例1的无支撑局部超挖区长度B=5和15 m时,各工况的支护桩桩身最大弯矩及变化系数见图8。支护桩最大弯矩沿基坑长度方向的传递变化规律与桩身侧移类似,沿基坑长度方向上的变化速率和桩身最大弯矩随局部超挖深度的增加而变大,局部超挖范围内弯矩及变化速率最大,随着与超挖区距离的增大,弯矩逐渐减小并趋于稳定,故用弯矩变化系数mi对其影响范围进行评价。

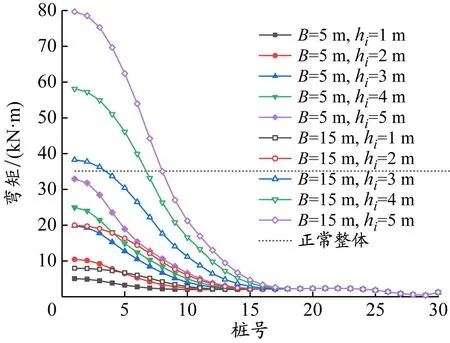
(a)最大弯矩曲线

算例1中各支护桩最大弯矩见图8(a)。在局部超挖深度hi=5 m,局部超挖长度B=5 m时,最大弯矩为32.92 kN·m,是初始弯矩参考值(35.13 kN·m)的0.94倍。当B=15 m时,最大弯矩为79.66 kN·m,是初始弯矩参考值的2.27倍,此时存在弯矩超限风险。

算例1的局部超挖长度B=5和15 m的弯矩变化系数见图8(b)。若定义弯矩变化系数mi>1.1为超挖区弯矩影响范围,则根据mi可确定算例1无支撑下局部超挖的弯矩影响范围(见图9)。无支撑下局部超挖,当局部超挖长度不变时,桩身最大弯矩影响范围与超挖深度呈二次函数关系。

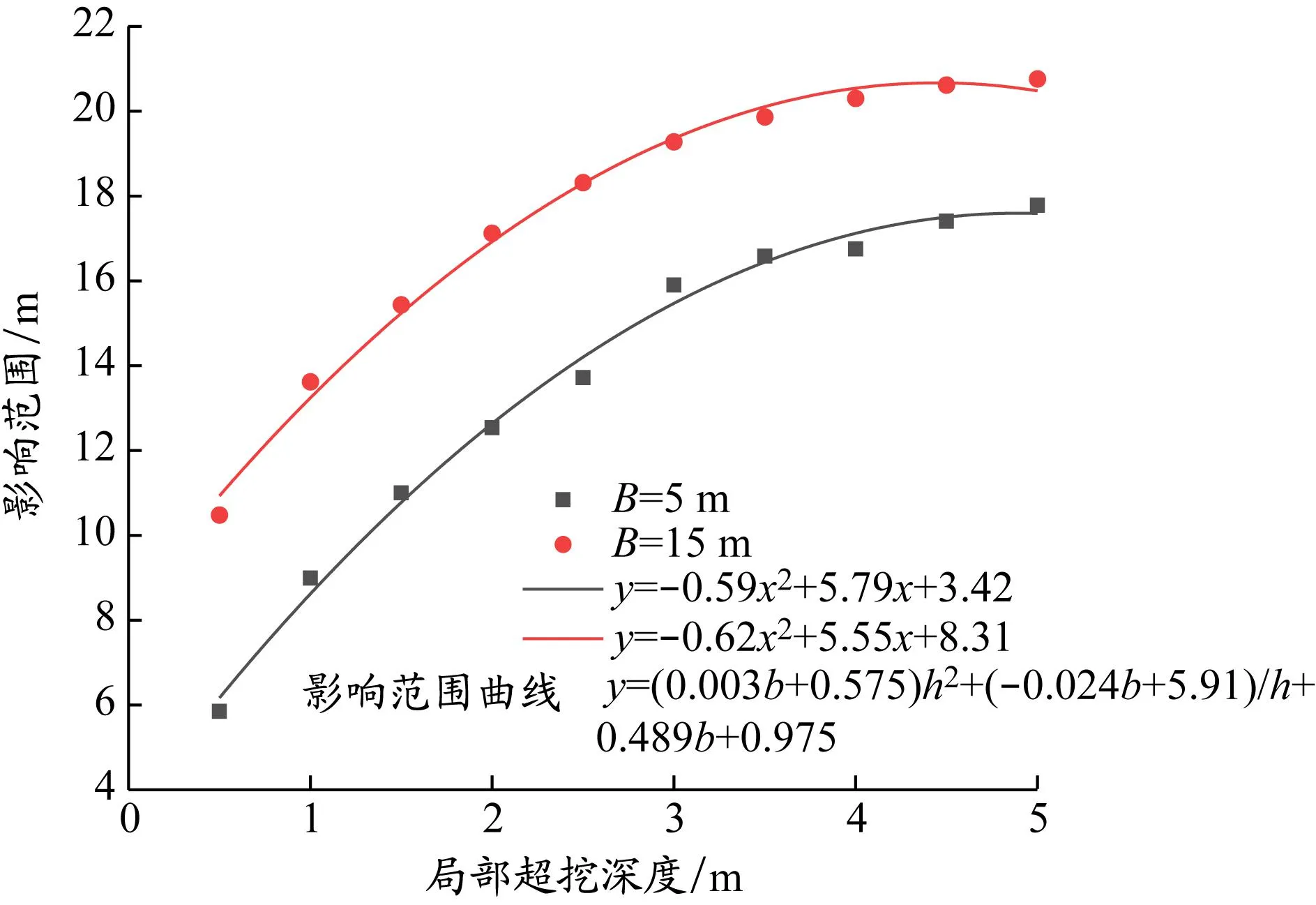
图9 算例1的最大弯矩影响范围

结合前文对桩身最大侧移的分析,绘制侧移和弯矩曲线,见图10。对局部超挖深度和长度进行控制,当无支撑、局部超挖长度B=5和15 m时,侧移与弯矩都应作为控制指标。若以1.1倍初始参考值及规范控制值二者中较小值为控制值,则局部超挖深度最大应控制在2.5～4.0 m。以局部超挖长度B=15 m为例,根据弯矩和侧移控制值可以得出,局部超挖深度最大可为2.5 m。

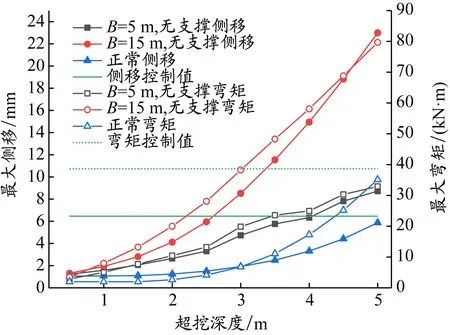
图10 算例1的侧移和弯矩曲线

4 有支撑下局部超挖

4.1 有支撑下局部超挖支护桩侧移

以算例2的1道支撑和算例3的2道支撑下局部超挖为例进行分析。如图11所示为局部超挖区长度B=5和15 m时,各超挖深度的支护桩桩身最大侧移。未进行局部超挖时,桩身最大侧移位置在大面积开挖底面附近,随着局部超挖深度的增大,其所在深度不断下移。沿基坑长度方向上,当距离超挖中心超过25 m时,支护桩侧移变化值已趋于稳定,侧移变化系数ki也在0.9～1.1,视为已超出局部超挖侧移影响范围。

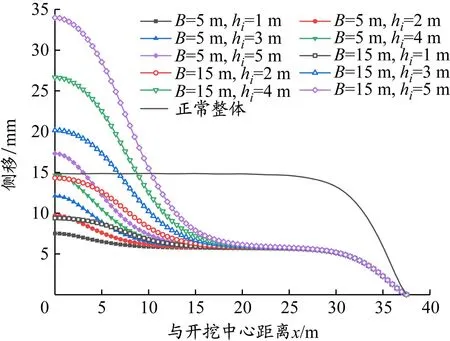
(a)算例2

算例2中的初始侧移参考值为算例4正常开挖10 m处沿基坑长度方向上支护桩身最大侧移(14.88 mm)。算例2的支护桩最大侧移分布规律与算例1类似,在局部超挖区长度B=5和15 m,局部超挖深度hi分别为4、2 m时,支护桩最大侧移已接近初始侧移参考值。局部超挖深度hi=5 m,B=5和15 m时,支护桩侧移值分别为17.33和33.99 mm,位移增量是初始侧移参考值的16%和128%。

算例3的初始位移参考值对应算例4正常开挖15 m处沿基坑长度方向上支护桩身最大侧移(28.58 mm)。在局部超挖区长度B=5和15 m,局部超挖深度hi分别为4、2 m时,支护桩最大侧移已接近初始侧移参考值。与算例2相同,局部超挖深度hi=5 m,B=5和15 m时,支护桩侧移值分别为31.31和51.99 mm,位移增量是初始侧移参考值的9%和82%。根据规范[23],若为一级基坑,算例2和3的水平位移控制值都为30 mm,故除了算例2中B=5 m时,其余工况中hi=5 m时,均存在位移超限的风险。

由有支撑的局部超挖最大桩身侧移确定桩身最大侧移变化系数ki,进而确定有支撑条件下局部超挖的侧移影响范围分布,见图12,发现侧移影响范围大致符合二次函数y=ax2+bx+c,各系数含义和数值见表4。

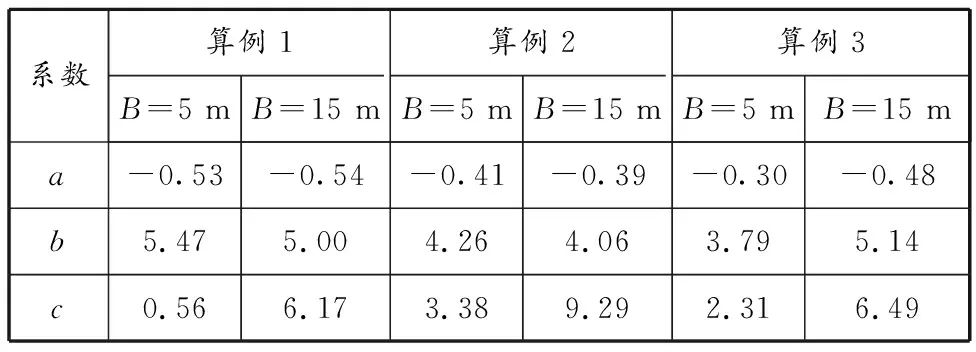
表 4 侧移影响范围

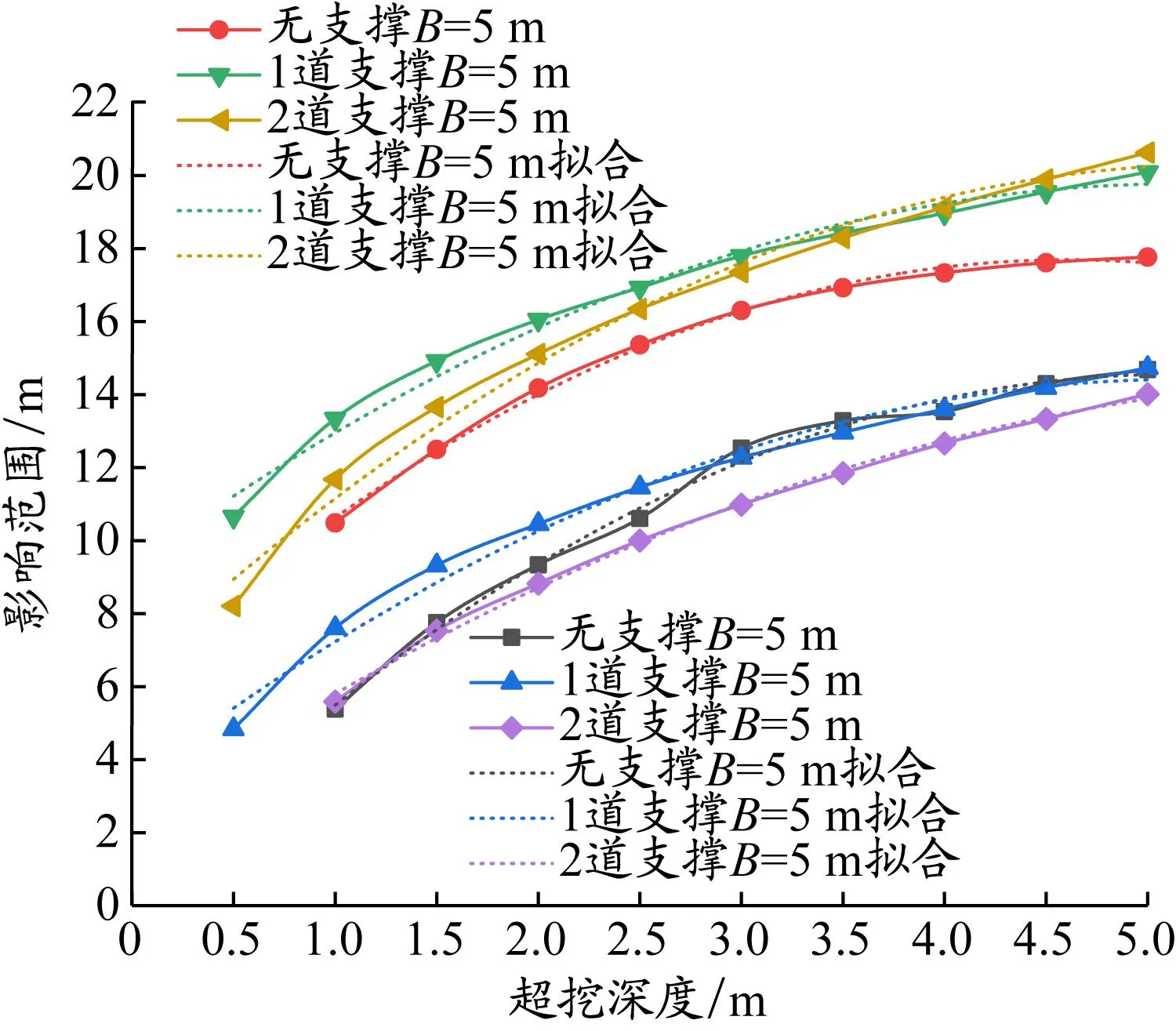
图12 局部超挖深度与侧移影响范围

根据侧移变化系数,可以得出无支撑条件下局部超挖桩身最大侧移的影响范围,超挖区长度与影响范围也近似为二次函数关系。

4.2 局部超挖下的桩后土压力

算例2和3分别取局部超挖时坑底以下2 m以及未开挖之前的支护桩后土压力,根据式(2)确定其土压力变化系数,见图13,趋势同算例1的无支撑下局部超挖情况。尽管算例1～3支撑逐渐增加,支撑的作用在一定程度上抑制了桩后土压力的变化,但算例1～3开挖深度逐渐增加,桩后土压力的变化幅度增大。

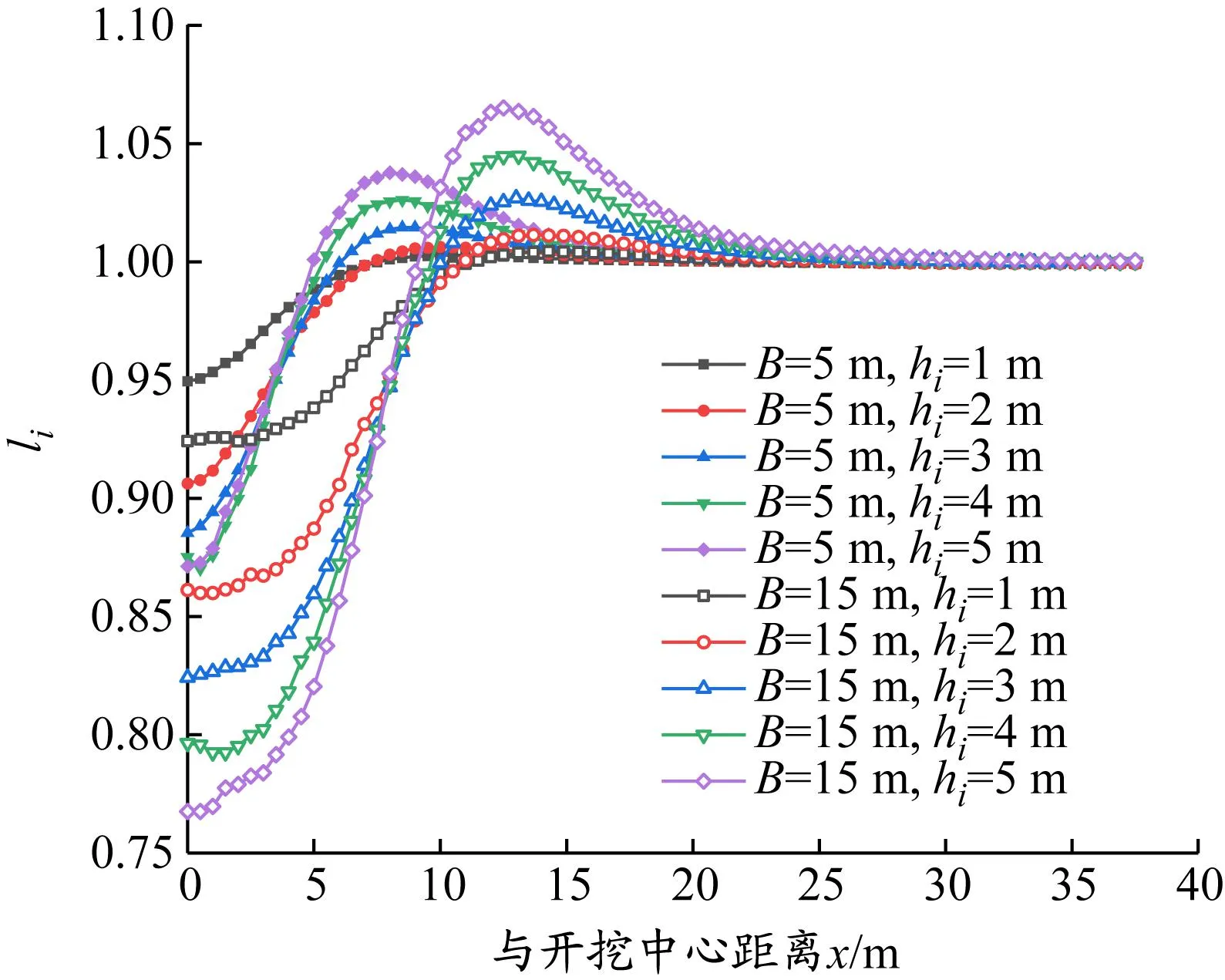
(a)算例2

在基坑长度方向上,局部超挖范围附近桩后土压力变化系数呈增长趋势,并在邻近区域内达到峰值,然后桩后土压力随着与局部超挖位置距离的增大而减小至1。由li稳定在0.99～1.01时,可确定其土压力影响范围,见图14。虚线代表li>0.99的范围,实线代表li<1.01的范围,影响范围取二者的交集。以算例1无支撑下局部超挖中超挖区长度B=15 m为例,随着局部超挖深度hi不断增加,当hi>0.5 m时,li>0.99的区域基本稳定在y=7 m处;而当hi>2 m时,开始有li>1.01的值,此时土压力影响范围以li<1.01和li>0.99的范围交集为准,故影响范围在hi=2 m处开始有突变。

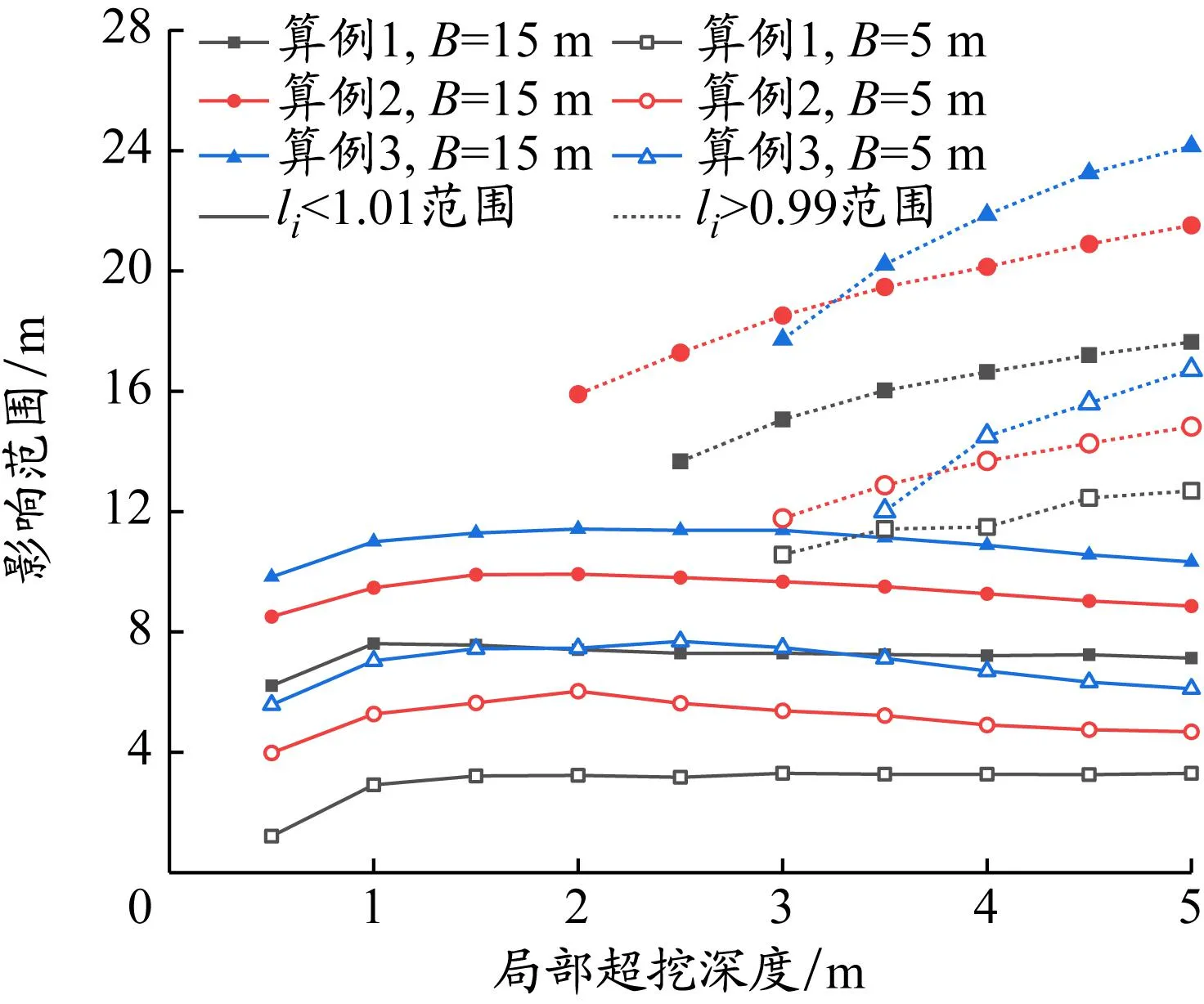
图14 局部超挖深度与土压力影响范围

4.3 支护桩最大弯矩

有支撑下局部超挖时,由于开挖深度已较大,此时起控制作用的是桩后主动土压力产生的弯矩,有支撑条件下局部超挖的最大桩身弯矩变化系数mi见图15。在算例2和3中,局部超挖区长度B=5 m时,随着局部超挖深度hi的增加,弯矩并未达到初始参考值;当B=15 m,hi分别为2.5、2.0 m时,弯矩已经接近初始参考值。根据mi确定其局部超挖深度与桩身最大弯矩的影响范围见图16。当局部超挖深度hi>a/5(a为基坑宽度)时,hi与弯矩影响范围呈线性关系。

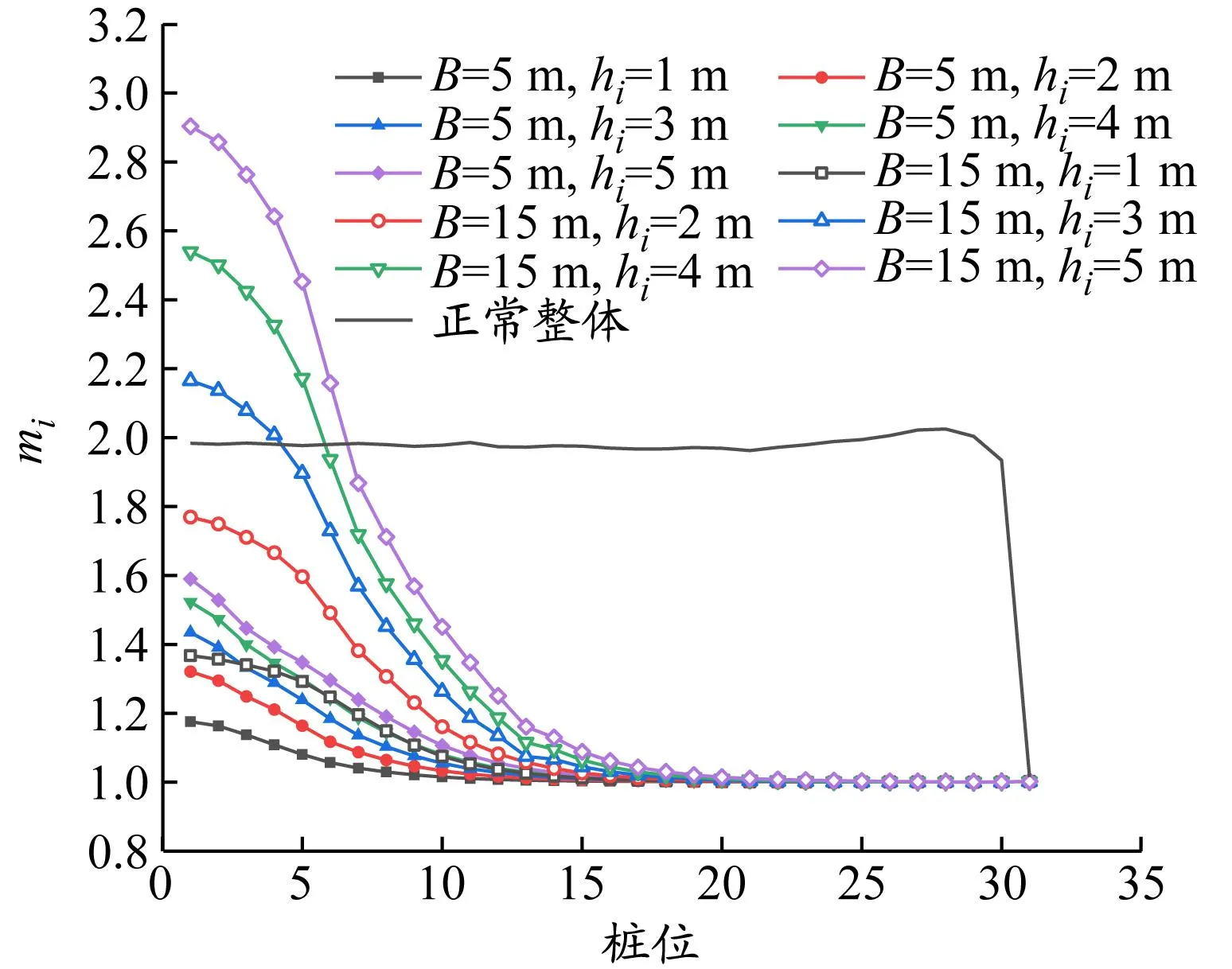
(a)算例2

图16 有支撑下局部超挖弯矩影响范围

以弯矩和侧移规范允许值以及正常支撑大面积开挖到相同深度的弯矩和侧移值作为初始参考值,取容许值与初始参考值中较小值作为控制值,综合考虑局部超挖范围及深度,用于控制实际施工中局部超挖的量。如图17所示,同样有支撑下局部超挖情况,若以1.1倍初始参考值及规范控制值二者中的较小值作为控制值,综合考虑弯矩以及侧移,则有支撑下局部超挖深度最大应控制在2.0～3.5 m。如算例2中第1道支撑下局部超挖,当局部开挖长度B=15 m时,根据弯矩和侧移控制值可以得出,最大局部超挖深度可为1.5 m,在B=5～15 m时也可根据图17确定其局部超挖深度。

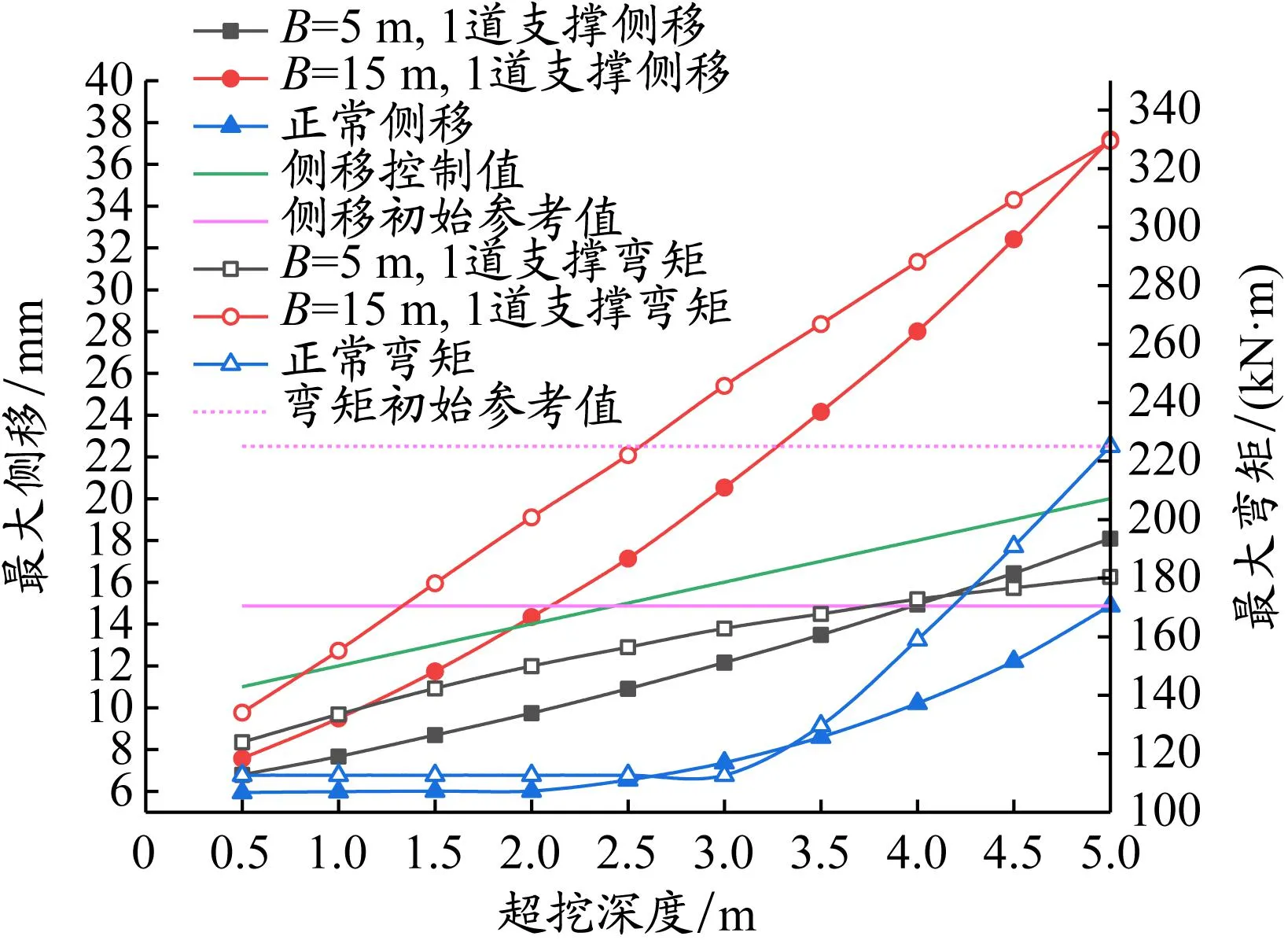
(a)算例2

4.4 支撑轴力

引入支撑轴力变化系数ni,定义当支撑逐渐远离超挖中心,ni稳定于0.98～1.02,则认为该支撑轴力不再受局部超挖影响。如图18所示,算例2在1道支撑下局部超挖,位于局部超挖区域内的内支撑轴力大幅增加,而邻近区域支撑轴力会小幅减小,远离局部超挖区后趋于稳定。

图18 算例2的第1道支撑轴力变化系数

图18中支撑轴力的变化趋势与图13的土压力变化趋势相符,第1道支撑主要承担由于局部超挖时第2道支撑未架设而转移的坑外主动土压力。根据轴力变化系数ni,当B=5和15 m时,轴力影响范围为4根支撑和5根支撑,换算为长度,即2种局部超挖长度下,各超挖深度的轴力影响范围均为b+3a。

如图19所示,算例3的第2道支撑下局部超挖时,此时第2道支撑轴力迅速增大,第1道支撑轴力逐渐减小,这种趋势随局部开挖区深度和长度增加而增强,第2道支撑主要承担由于局部超挖时第3道支撑未架设而转移的坑外主动土压力。

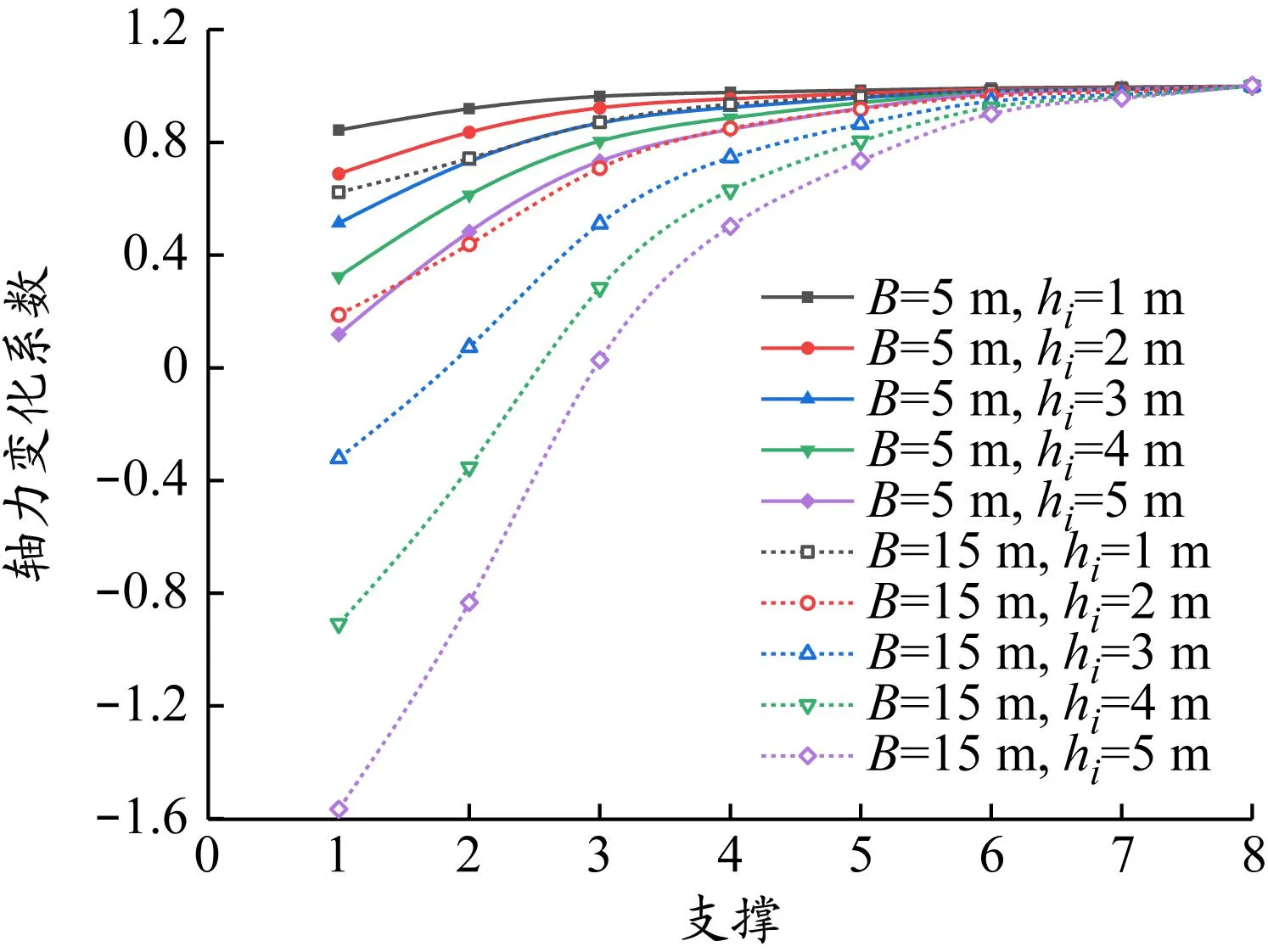
(a)第1道支撑

当局部超挖区长度B=15 m时,若超挖深度hi>2 m,则第2道支撑轴力的影响范围为b+3a,第1道支撑轴力的影响范围接近b+4a。此时,超挖区及其附近的第1道支撑会出现拉应力,原因类似于支撑滞后[27],支护桩下部缺乏第3道支撑约束,在土压力作用下踢脚变形过大,支护桩以第2道支撑为支点发生旋转,支护桩底部向坑内,顶部向坑外移动,减少对内支撑的压力。此时要注意发生失稳的可能,如首层支撑为钢支撑,局部超挖则有可能使其出现拉应力,容易发生事故。对比轴力变化系数,得出算例3的第2道支撑下局部超挖对支撑轴力影响最大,与前文弯矩侧移变化相符。