寻找错题原因 寻求教学对策
——低年级学生“三位数退位减法”错误探源
2024-01-07浙江省湖州市湖师附小教育集团井安小学费云龙
浙江省湖州市湖师附小教育集团井安小学 费云龙
一次家长开放日上,在教学人教版数学三年级上册“三位数退位减法”时,家长都惊讶这么简单的内容竟然上了40 分钟。在课堂上,学生积极举手说三位数退位减法的算理和算法,好不热闹。可是当他们独立完成作业时,总出现这样或者那样的错误。每当让他们订正时,大部分学生又能做正确,因此,很多家长都把它归因于粗心、不认真等。那么,如何帮助这些有困难的学生呢?笔者认为,首先应该了解他们在计算过程中的真实思维,找出他们出现错误的真正原因,并采取相应的对策,才能帮助他们改正错误,使他们获得学习上的成功。
为此,针对作业中的“408-299”一题,笔者经过收集、比较和分析,发现主要存在以下三种类型的错误。
错误类型一:抄错数字或符号——视知觉能力发展失衡
1.学生错误再现
师:(给生1 看图1)这道题目哪里错了?
生1:哦,我把减号看成了加号。
师:(给生2 看图2)这道题目哪里错了?
生:(看了6 分钟左右)老师,我也不知道哪里错了。
师:(递给他一张纸条)请你圈出下面数字中的9899:
8888 8889 8898 8988 9888 8899 8989 9889 8998
9898 9988 9998 9989 9899 8999 9999 8889 8898
8888 8889 8898 8988 9888 8899 8989 9889 8998
(该生花了很长时间,还是没有全部圈出来)
师:请你再读一次题目。
(这时该生意识到自己在8 和9 这里出了问题,再认真地看了一遍,说:我把题目中的8 抄成了9)
2.心理分析:视知觉能力发展失衡导致不协调
学生抄错数字或符号的主要原因:一是学生做题时视觉不集中;二是学生视觉分辨困难、视觉不协调。
由此可见,教师要区别对待不同原因导致的错误。如生1 是由于做题时注意力不集中导致出错,可以建议他养成做完作业后再检查的习惯;生2 可能是对数字的概念模糊,导致他混淆了8 和9。
3.寻求对策:对症下药与等待发展
对策一:养成整体抄题的好习惯
由于低年级学生视觉发展规律,个别学生抄题时常常是看一眼记一个数字,再看一眼再记下一个数字,这样的抄题习惯不仅费时,还容易看错。因此,教师在平时要引导学生用一个整体字节来进行短时记忆,这样做既能节约时间,还能训练学生的短时记忆力。
对策二:学会完成题目后“回头看”
如果学生在列竖式计算时能马上做对那是最好的,如果不能就需要在写完竖式后“回头看”自己的作业,即检查计算过程,或者用加减法“验算”,及时发现自己作业中的计算错误。
对策三:加强学生视直觉的训练
个别学生的视直觉发育不完全,因此,教师可以通过舒尔特表、找不同的数、找相反的数、辨别相似字母、图形仿画等形式,帮助这类学生的视直觉能力达到平衡,也可以让这类学生用以下步骤来纠正自己的错误:第一步,将题目读出声来,并把题目记录下来。第二步,把自己记录下来的题目读一次。第三步,比较自己两次读的是不是同一道题目。
教师通过这样步步强化,让学生看清楚题目,避免因为抄错题目出现的计算错误。
错误类型二:退位混乱——思维能力造成思维“短路”
1.学生错误再现
师:(出示图3、图4)你是怎么做“409-299”这道题目的?

图3 生3 的解题过程

图4 生4 的解题过程
生3:我是这样做的,8 减9 不够减,向十位借1,十位没有,再向百位借1。个位上18 减9 等于9,十位上10 减9 等于1,百位上4 减1 减2 等于1。
师:十位上的这个退位点不写可以吗?
生3:不可以。
师:十位上既然写了退位点,就应该退位,是吗?
(生3 点点头表示同意)
生4:我是这样做的,8 减9 不够减,向十位借1,十位没有,再向百位借1。个位8 减9 等于9;十位0 减9不够减,再向百位借1,10 减9 等于1;百位4 减1、减1再减2 等于0,不写。
师:你为什么要向百位借两次?
(学生沉默不语)
2.心理分析:计算步骤与短时记忆造成思维“短路”
通过与学生对话,笔者发现学生在用竖式计算这道题目时因为需要多次退位导致思维“短路”。主要原因是:
(1)计算步骤多
学生在用竖式计算被减数中间有0 的连续退位减法时,需要清晰地理解三位数退位减法的算理和算法,才能正确完成竖式计算。因此在教学过程中,教师应当反复强调算理和算法,如可以借助计数器(如图5)帮助学生理解算理。
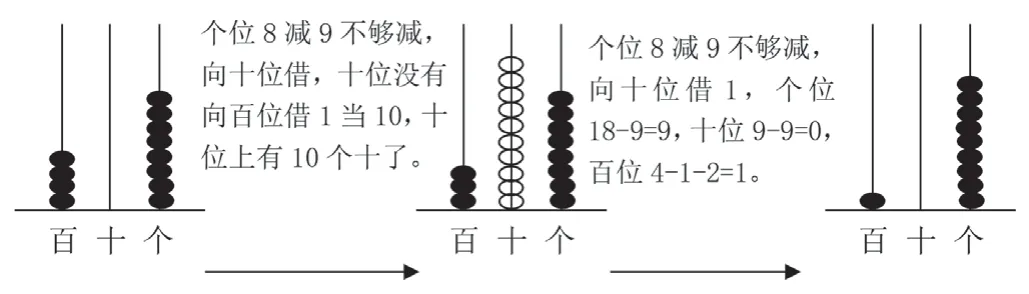
图5
借助直观、动态化的演示,教师可以让学生清晰地了解连续退位的过程,便于学生把看到的过程用数学语言描述出来,在竖式计算中表示出来。
(2)短时记忆量大
由于计算步骤较多,学生没有经过计数器或小棒操作,就需要把退位的过程记录在自己的脑海里。而低年级学生的短时记忆时间短,限制了他们掌握竖式计算。
3.寻求对策:过程化记录思维过程
针对上述错误原因,笔者认为,可以用书面或者口语的形式记录学生的思维过程,减少他们在计算过程中的记忆量。
对策一:改变书写格式,记录思考过程
对于容易做错这类题的学生,可以让他们在竖式上记录自己的思考过程(如图6),以此来提高解题正确率。
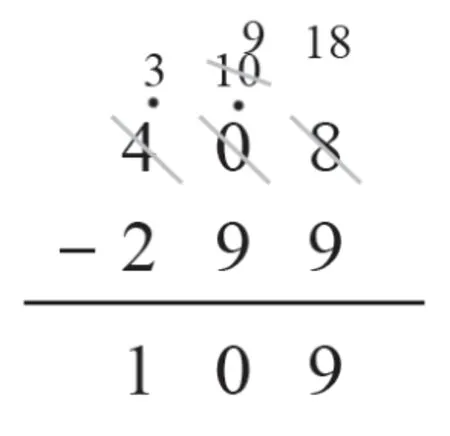
图6
对策二:边说边算,出声说计算过程
对于学困生,教师可以让他们边摆计数器边说算法,再过渡到看着竖式说算法,最后默说竖式的算法。这样的出声训练,可以将学生隐性的思考过程显性化,既有助于教师发现学生出现错误的原因,也方便学生检查对方的计算过程。
学生通过一定量的练习,实现竖式计算思考过程的“自动化”后,教师可以减少这样的练习。
错误类型三:口算错误——基础知识不熟练造成思维“混乱”
1.错误再现
师:(出示图7)你是怎么做这道题目的?
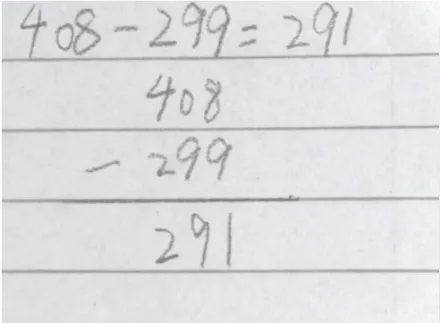
图7 生5 的解题过程
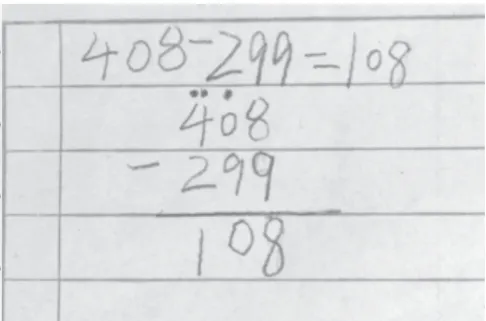
图8 生6 的解题过程
生5:我是这样做的,个位上9 减8 等于1,十位上9 减0 等于9,百位上4 减2 等于2。
师:我们平常做减法的时候都是从上往下减的,你为什么从下往上减呢?
生5:哦,我忘记了。以前做减法时也这样从下往上减。
生6:我是这样做的,8 减9 不够减,向十位借1,十位没有,再向百位借1。18 减9 等于8;十位0 减9 不够减,再向百位借1,10 减1 减9 等于0;百位4 减1 再减2 等于1。
师:你再想想18 减9 等于多少。
生6:我错了,等于9。
2.心理分析:基础知识不熟练造成思维“混乱”
通过再现学生的思考过程,笔者发现生5 和生6 出现错误主要原因:
(1)不够减时“倒着减”
生5 出错的主要原因是他在做减法遇到不够减的情况时 “倒着减”。这源自学生首先接触的是不退位减法,大量的“大数减小数”练习让学生形成了思维定式。
(2)口算能力弱
生6 出错的主要原因是20 以内加减法计算基础不扎实,尤其是20 以内的进退位加减法,如他把这道竖式计算中的18 减9 算成8。
3.寻求对策:狠抓基础读口算
策略一:搭建“脚手架”复习旧知
针对学生在计算三位数退位减法时出现知识性遗忘的现象,教师可以出示两位数退位减法,如56-19,帮助学生回忆两位数退位减法的竖式计算,不够减要向前一位借1 当10,与原来的数合并再减。教师通过这样的复习,帮助学生自然地过渡到三位数退位减法,就能有效避免“倒着减”的现象。
策略二:借助课前1 分钟多读口算
20 以内的加减法是小学阶段加减法计算的基础,因此20 以内加减法的计算速度也影响着学生进行三位数退位减法计算的快慢。教师可以让学生在课前1 分钟自由朗读20 以内加减法口算,让他们看到这些口算题时就能将答案脱口而出,从而减少在更加复杂的计算中的错误。
总之,教学处处有细节,教师不应该把学生的错误简单地归因于“粗心”,从而机械重复操练巩固技能,而应根据学生的心理特征和思考过程,追根求源,真正寻找到错误的原因,并探究出切实有效的对策,帮助学生减少在三位数退位减法计算中的错误。
