极小样本数据的不确定度改进灰色评定方法

朱彦龙, 程银宝, 高宏堂, 王 燕,施江焕, 罗 哉, 李亚茹

(1.中国计量大学，浙江 杭州 310018； 2.中国计量科学研究院，北京 100029；3.沈阳飞机工业(集团)有限公司，辽宁 沈阳 110850；4.宁波市计量测试研究院，浙江 宁波 315048)

1 引 言

近年来,非统计不确定度评定方法的研究极大地促进了不确定度理论的发展,其中灰色系统理论评定不确定度的方法凭借着无需数据分布,对小样本同样适用[1]等优点吸引着不少学者。工程应用中,样本容量n满足10≤n≤30时为小样本,当样本容量n<10时为极小样本[2,3]。由于极小样本数据所含的信息量极少,评定其不确定度困难较大,用传统灰色方法对极小样本数据的不确定度评定问题进行的研究非常少,这些研究表明,经典灰色系统理论评定不确定度在从小样本到极小样本的过渡过程中,标准差计算结果的相对误差在迅速增大[4],因此有必要研究灰色系统理论在极小样本条件下的改进算法。

Ma等通过Bootstrap技术研究小样本数据集的不确定度问题,并用实例分析了该方法的可靠性[5];Wang 等提出了小样本数据的灰自助处理方法,并与灰色系统理论、自助法做了对比,得出结论灰自助法在小样本动态信号估计方面具有优势[6];郭晓娴等通过虚拟样本增广方法与Bootstrap方法,对样本量为1的数据进行扩充,进而研究了轴承磨损寿命的可靠性评估问题[7];Cao等混合了虚拟样本增广法和Bootstrap法,证明了混合方法比半经验法在解决极小样本数据问题上更加有效[8];王中宇等通过径向基函数(RBF)神经网络和灰色系统理论解决了小样本虚拟仪器测量不确定度的评定问题[9];黄家成提出基于灰色系统理论和贝叶斯信息融合理论评定小样本自动测试系统(automatic test system,ATS)测量不确定度的新方法[10];Han针对小样本和未知分布提出了一种基于灰色关联系数的测量不确定度的灰色评价方法[11]。

由于极小样本数据的信息缺失较为严重,灰色系统理论难以从中提取出规律,评定不确定度时出现较大偏差,因此,提出改进的灰色不确定度评定方法,认为极小样本数据是一组不平衡数据集中的少数类,通过改进的合成少数类过采样技术(synthetic minority oversampling technique,SMOTE)挖掘原始样本所蕴含的信息,再通过支持向量回归(support vector regression,SVR)模型从挖掘得到的信息中预测一定量的样本,最后将所得预测数据与原始数据融合为灰色小样本数据集,进行灰色不确定度评定。最后通过计算机模拟数据与实验数据分别验证了模型的可靠性和泛化性。

2 不确定度灰色评定原理及改进

2.1 测量不确定度灰色评定原理

灰色系统理论按照颜色来区分不同的系统,其中“灰”是介于“黑”和“白”之间的,黑色系统是指系统的输入输出等表层关系已知、系统内外部变化关系不明确、系统内部结构原理未知的系统,白色系统是指系统的所有信息都明确的系统,而其他处于两者之间的系统,就是灰色系统。一个测量系统是一个典型的灰色系统,测量得到的结果就是灰色量。灰色系统理论提出采用累加生成的数据处理方式探求数据中的内在规律[12]。

2.2 改进的测量不确定度灰色评定原理

2.2.1 SMOTE原理分析

SMOTE[13]是一种过采样方法,通过在少数类样本之间线性插值以获得人工合成样本,改善数据的均衡性。运用SMOTE合成新样本的基本原理如图1 所示。

图1 SMOTE合成新样本原理

设有一少数类X,样本量为n,对于每一个少数类样本xi,(i=1,2,…,n)通过计算xi与xj(j=1,2,…n且j≠i)之间的距离找到xi的k个近邻样本,随机挑选一个近邻样本xl与xi构成一条线段,通过式(1)进行线性插值合成新的样本xnew。

xnew=xi+rand(0,1)×(xl-xi)

(1)

式中:rand(0,1)指区间[0,1]上服从均匀分布的随机数。上述过程重复N次,可合成(n×N)个样本。

2.2.2 SVR原理分析

SVR是由支持向量机(SVM)引申出的数据回归模型,其关键在于寻找一个能够使最多样本点分布在其附近的超平面,对于非线性问题,已知样本D={(x1,y1),(x2,y2),…,(xn,yn)},设样本空间的样本点经过映射ψ(x)变换到高维的特征空间,则超平面方程可表示为f(x)=wTψ(x)+b,其中w为超平面的权向量,b为偏置向量。SVR的求解模型为:

(2)

(3)

ε为不敏感损失参数,根据需要取定。解算后SVR模型的形式[14]如下:

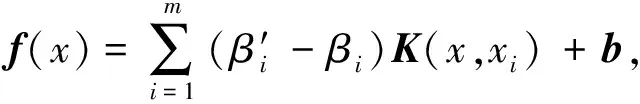
i=1,2,…,n

(4)

2.2.3 改进的测量不确定度灰色评定模型

对于极小样本的测量数据列X,假设其服从某分布P,而服从P分布的所有数据构成数据集D,则数据集D具有不平衡的特性,即已知数据列X与未知数据列(D-X)的样本数量不在同一个数量级。想要通过X直接估计数据集D的参数较为困难,SMOTE算法思想可以有效地改善数据集的不平衡特性。

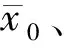
(5)

设置n为5、q为100、k为3,运用原始的SMOTE算法后,可以发现式(5)恒大于0,即表明运用原始SMOTE算法合成大量的新样本将造成数据列的离散性降低,改变了极小样本数据列的信息,这与本文将运用SMOTE挖掘极小样本信息的目的不符。为了能够改善上述问题,对模型(1)进行改进,将模型中的rand(0,1)改为rand(a,b),其中参数a、b与原始样本数量与合成新样本的数量有关,在(0,1)区间两侧对称取值。则SMOTE的数学模型变为:

xnew=xi+rand(a,b)×(xl-xi)

(6)

为了确定参数a、b的值,通过计算机随机生成5 000组极小样本数据列,每组的样本容量为5,各组单独进行实验,则进行SMOTE时n=5、q=100、k=3。每组实验中,确定最优的a、b值,使新合成的样本与原始样本混合后的标准差和混合前原始样本的标准差在保留2位有效数字的情况下相等。实验完成后对a、b值进行统计,统计结果详见图2。结果表明,a值有99%的概率落在[-0.8,-0.4]范围内,b值有99%的概率落在[1.4,1.8]范围内,则a、b分别取峰值-0.6和1.6时可以使模型(6)具有最大的泛化性。

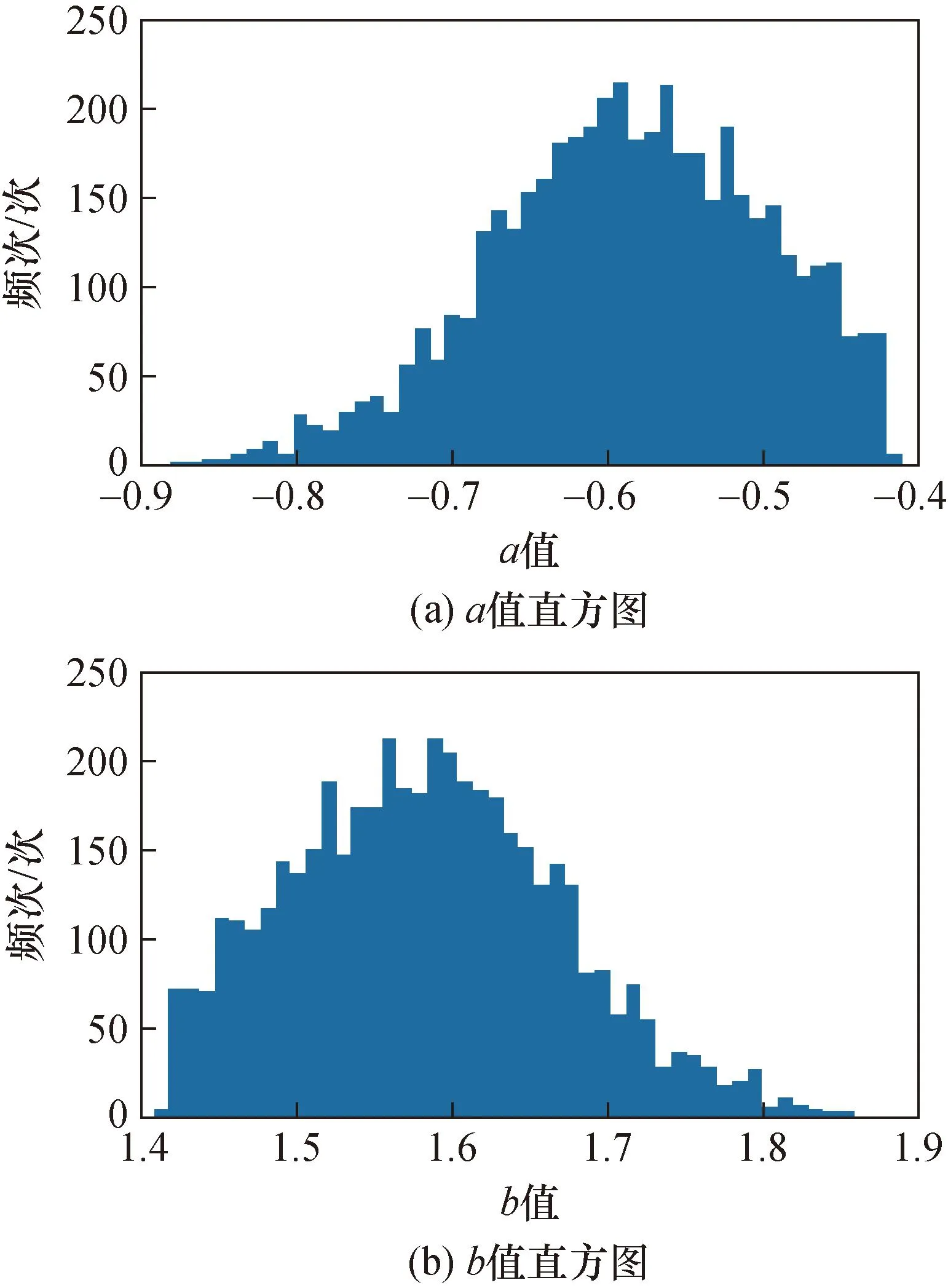
图2 a、b值统计特性

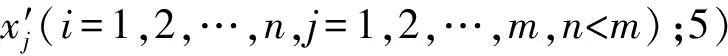
(7)

式中:c称为灰色常系数,其大小通过计算机算法仿真得到,通常可取2.5。

SMOTE的原理决定了其合成的新样本具有一定的浮动性,但同一次SMOTE后的若干组预测数据的标准差之间满足统计规律,对某随机数据列执行上述步骤1)～3)后循环执行步骤4)～10) 共5 000次,对5 000次运行结果进行统计,得到如图3(a)所示的直方图,由图可知服从正态分布,取均值表示此次SMOTE后的数据标准差普遍水平。同时,对于同一组原始数据进行多次SMOTE后,其普遍水平同样出现浮动,但浮动幅度到了非常小的范围,进行5 000次SMOTE后的标准差普遍水平有图3(b) 直方图,再取均值即表示此组原始数据标准差的水平。

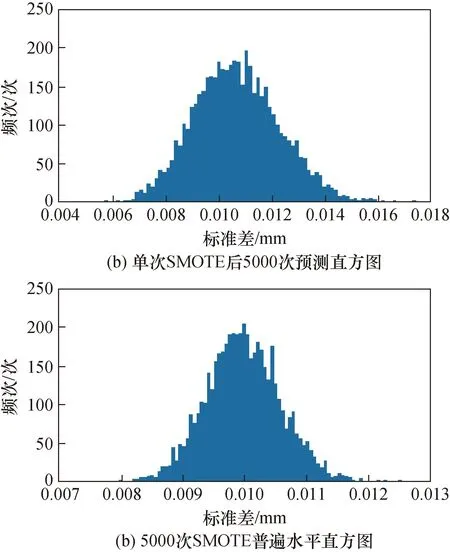
图3 新合成样本标准差统计特性

2.3 改进效果分析

经典灰色方法对原始数据不做处理,直接进行累加生成,因此对样本容量提出了要求,即对于小样本及以上样本容量的数据,所包含的信息量较多,经典灰色方法都可以处理,但却不适用于极小样本数据。

通过改进,在经典的灰色方法中加入了SMOTE-SVR模型,首先对原始数据进行处理,通过学习数据规律,将极小样本扩充到小样本,再进行累加生成。灰色方法改进前后的区别如图4。

图4 改进前后对比

3 仿真分析

为验证上文提出方法的可行性,本节使用计算机对多种分布进行抽样,模拟测量数据,不确定度评定过程中,使用较多的数据分布类型有正态分布、均匀分布、三角分布等,则本章对此3种分布类型的模拟数据进行验证。生成9组极小样本数据如表1,其中每组数据的样本容量为5,各组独立不相关。

表1 模拟生成的9组极小样本量数据

贝塞尔公式和极差法在不确定度评定领域具有普遍的可接受性[15],为了直观地表示改进的灰色方法相较于经典灰色方法的改善能力,以极差法的计算结果作为参考值,定义改善率η如式(8)。

(8)

式中:σimp_g表示改进灰色方法得出的标准差;σg表示经典灰色方法得出的标准差;σr表示极差法得出的标准差。η为正则表示具有积极的改善作用。

分别运用贝塞尔公式法、极差法、经典灰色方法和改进的灰色方法计算标准差,计算结果如表2。

表2 不同方法计算模拟数据标准差

表2数据表明,所提出的改进灰色方法的计算结果具有较高的可靠程度:相比于经典灰色方法,改进后的灰色方法在结果上有不同程度的正向改善,改善率分布在8.33%～41.18%;表格中数据也表明改进的灰色方法具有较好的泛化能力:对多种分布的极小样本数据都表现出适用性。改进的灰色方法更适用于极小样本数据的不确定度评定。

4 实例分析

经上述分析,改进的灰色方法在模拟数据上具有可靠性,以某航空发动机高空模拟试验的空气流量测量中的总温数据为例,运用极差法、经典的灰色方法、改进的灰色方法分别进行不确定度A类评定,通过比较验证改进的灰色方法在极小样本量数据的不确定度评定中的优势。

图5为搭建的航空发动机性能测试系统示意图,总温指流量管主流区中的气流以绝热过程完全静止时,动能全部转化为内能时反映出来的温度[16]。实际测量中,在空气流量测量截面上,沿周向均匀布置6支测量耙,每支测量耙上有3个总温探针。总温探针的位置布置符合流量管3等环面要求,并且每个探针处于所在等环面的面积中心线上。总温测量的测量耙与总温针的布局如图6所示。

图5 航空发动机性能测试系统示意图

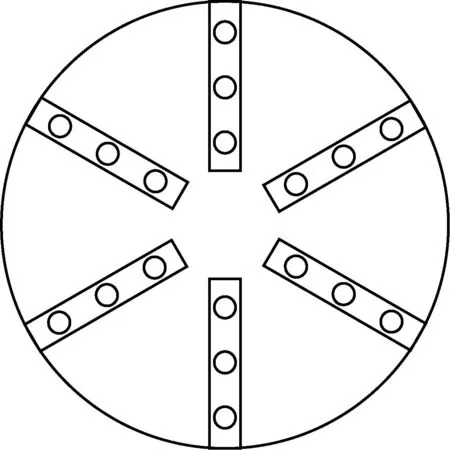
图6 总温测靶布局

对每个测靶的3个总温测点进行5次重复性测量,测量结果见表3。分别运用极差法、经典灰色方法、改进的灰色方法计算重复性,结果见表4。分析表4数据可知,改进的灰色方法能够应对航空发动机高空模拟实验空气流量测量中的不同总温数据情况,具有较高的可靠性和泛化性。对于经典灰色方法评定的重复性结果与参考值偏差较小的数据列,改进的灰色方法评定的重复性结果与经典灰色方法一致,对其中少部分数据列有改善,最高改善了50.00%;对于经典灰色方法评定的重复性结果与参考值偏差较大的数据列,改进的灰色方法也有不同程度的改善,最高改善37.50%。

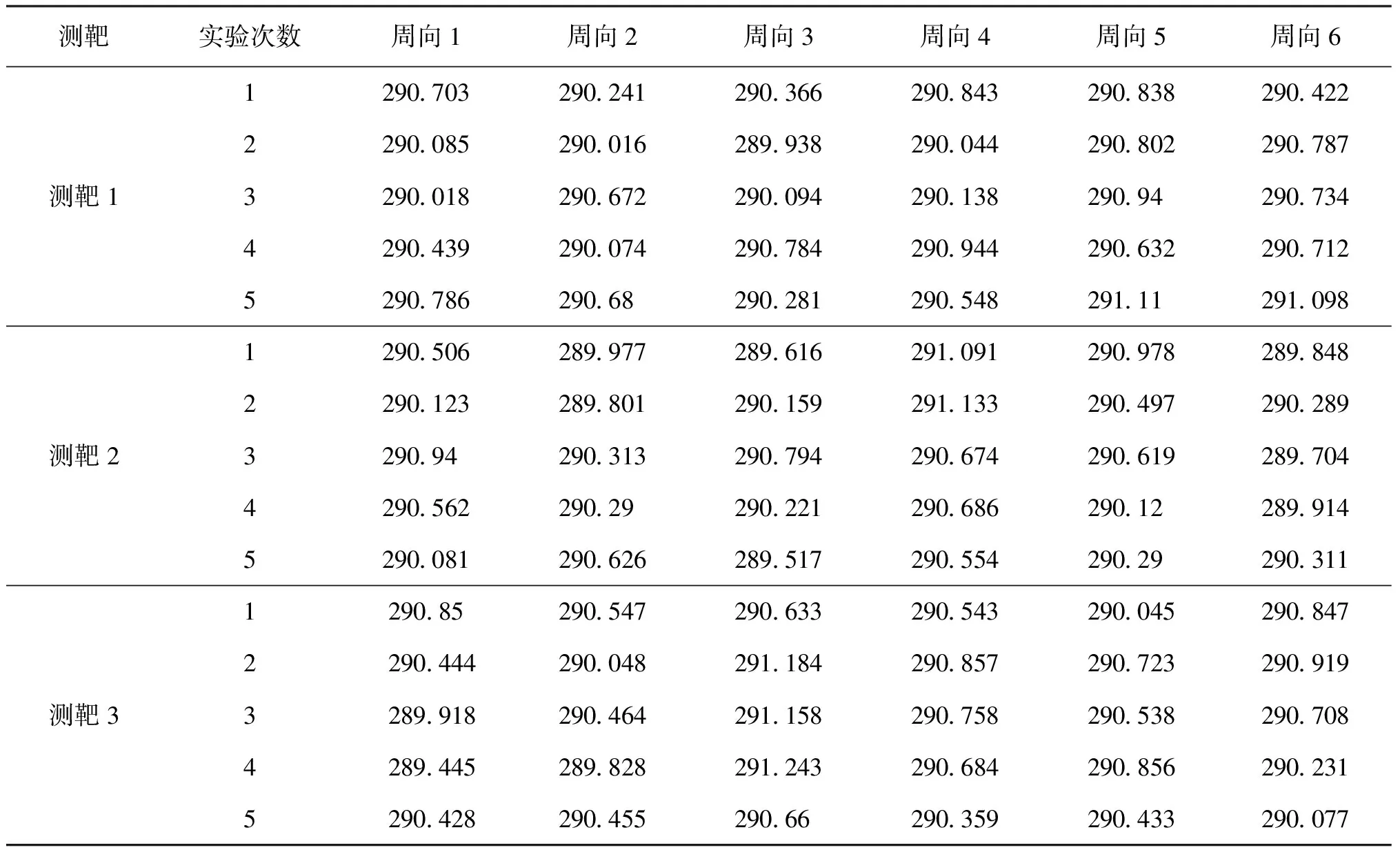
表3 总温重复性测量数据

表4 总温重复性计算结果

5 结 论

通过提出一种改进的测量不确定度灰色评定模型,以期能够解决经典的测量不确定度灰色评定模型在极小样本条件下局限性的问题。首先使用模拟的极小样本数据验证了该模型的可靠性、泛化性,相较于经典的灰色方法,改进的灰色方法对不同分布的数据均有改善作用,最高改善41.18%。以某航空发动机高空模拟试验的空气流量测量中的总温数据为例,验证模型的性能,用包括改进的灰色方法在内的不同方法评定重复性,改善率最高达50.00%。改进后的灰色方法能够有效突破经典测量不确定度灰色评定的局限性,可为极小样本的不确定度评定研究提供参考。