幅值可控的逆反射和镜像反射双通道超表面结构拓扑优化设计*

史鹏飞 马馨莹 向川 赵宏革† 李渊 高仁璟 刘书田

1) (大连海事大学船舶电气工程学院,大连 116023)

2) (武汉理工大学,光纤传感技术国家工程实验室,武汉 430070)

3) (大连理工大学,工业装备结构分析优化与CAE软件全国重点实验室,大连 116023)

1 引言

近年来,由于包括下一代移动通信等无线设备的高速发展,相关领域对多径传输特征表现出了突出的技术需求,反射面(体)的多通道反射特性引起了相关领域研究人员的重视,其中,对包含逆反射通道的多通道反射面(体)的研究显得尤为突出.逆反射是一种反射波沿其入射路径返回的特殊电磁、光学及声学物理现象,其满足广义斯涅尔定律,然而无法由自然界已有物质直接实现,为打破该限制,包括复晶格超光栅在内的一些特异反射机制被陆续提出[1-4].随着逆反射理论的深入和实现形式及工艺不断推陈出新,其已广泛覆盖光波段、厘米波及毫米波波段、声波波段,并在卫星定位、目标识别等领域表现出了巨大的应用潜力[5,6].自然物质自身并不具备与生俱来的逆反射特性,多通道反射中如何实现逆反射则成为了需要重点解决的问题.常用逆反射机制主要包括两种: 以金属角反射器、角形梯度光栅、U形反射波导为代表的局部立体空间内多次镜像反射或折射机制;以龙勃透镜为代表的空间材料的非均匀化引导机制[7-10].然而,已有反射器多以三维立体结构为基础,严重限制了其装备背景.为实现小型化的双/多向反射表面的逆反射通道,研究人员提出了基于相位调控的二维平面型逆反射通道实现机制[11,12].

2011年Yu等[13]指出相位差可由不同辐射单元结构实现,其使用不同V型谐振结构产生感应相位差,通过对其进行梯度相位的一维排列,实现了光波段的一维逆反射.基于此思想,进一步研究表明,在超表面阵列单周期内搭建被动金属格栅,各格栅相位响应差异使斜入射电磁波的梯度相位反向,该逆向梯度响应相位可产生反向波束赋形[14-16].基于梯度相位的逆反射实现机理,更多的梯度相位实现形式被提出用以满足不同的背景需求[17].针对离散型梯度相位超表面,推导表明基于梯度相位实现逆反射时单周期所需的最小格栅数为两个,单周期内两个结构产生360°的相位变化即可实现这种二进制逆反射器[18,19],该种二进制超表面可以实现高反射率的逆反射.文献[20]基于二进制超表面模型,以六边形作为最小格栅单元,设计了三向同性逆反射超表面.目前研究中逆向单通道反射得以实现,即在逆反射角方向获取高反射功率,而在保证逆反射方向具有一定反射功率比例同时具有常规镜像反射特性的反射器同样是被需要的.具有特定空间响应相位分布的非周期性超表面被发现可用于波的反射、折射等传播方向的控制,同样包括针对不同极化形式的逆反射,其基于不同阵元位置反射相位的叠加,然而该种超表面需要较大的阵列规模[21].文献[22-25]指出,以包含梯度相位的超胞阵列组成周期阵列,在不同的超胞边长与波长比时反射会在多反射通道内发生镜像反射、逆反射或寄生反射等多通道反射,一定比例下可同时实现镜像常规反射和逆反射,而对于如何控制各通道反射强度没有给出答案.

斜入射波激励下超表面产生包括逆反射的多通道反射中,超表面对不同通道表现出不同的梯度相位,同时表现出不同的响应阻抗,响应阻抗决定了对应通道反射功率,而基于一维排列栅型相位梯度超表面在梯度相位前提下调整响应阻抗目前仍没有系统的方法.反射器包含逆反射通道本身较难实现,在此基础上控制不同通道反射占比则变得更加复杂.以周期性超表面的一个超胞作为设计域,获取合理的贴片分布可实现周期内所需360°相位差,同时获取对应通道下具有所需阻抗的微结构成为重要的设计目标.拓扑优化在解决包括电磁微结构在内的均匀化材料设计中表现出优异的可行性,通过调整优化离散设计域内材料排布,获取具有最优模型特性参数的可行解.在逆反射超表面设计中,微结构对其响应具有决定性作用,微结构更充分的细节易于精确控制自身反射相位及阻抗特性;常规尺寸或形状优化难以找到设计域内针对相位及阻抗的共同敏感区域,而拓扑优化对局部区域有充分的考虑,同时获取合理的相位及阻抗特性,避免基于典型结构的尺寸优化受限于初始微结构的问题.

基于以上分析,本文对包含逆反射的双通道反射器实现模型进行了设计,提出了具有特定逆反射、镜像反射比值或占比的反射器微结构的拓扑优化方法,对其进行算例设计及验证,验证了所提方法的有效性.

2 包含逆反射的双通道反射机理

斜入射电磁波照射到常规反射表面,反射波沿不同反射路径到达同一出射点,则光程及到达相位均相同.设反射表面沿表面切向响应相位差为 dϕx,反射角θr与入射角θi的关系为

其中,k0=2π/λ0为波数,λ0为入射波波长,n0为介质折射率,无切向梯度下反射介质表面发生常规镜像反射.

然而,反射介质表面具有特定相位梯度时,则介质表面可满足一组以上入射、反射波和透射波边界条件,介质表面可能会表现出多通道反射特性.如果反射介质为周期性介质,则反射介质表面的反射通道数取决于其周期特性,当周期d小于入射波波长λ0,反射介质表面仅表现出通常的镜像反射,当d＞2λ0时,介质表面可能具有3个以上反射通道.周期λ0＜d≤2λ0的前提下,介质表面可能具有 +θr或 -θr向双通道反射[25],如图1所示.在该尺寸范围内设定周期尺寸,对(1)式进一步推导,即化为广义斯涅耳定律:

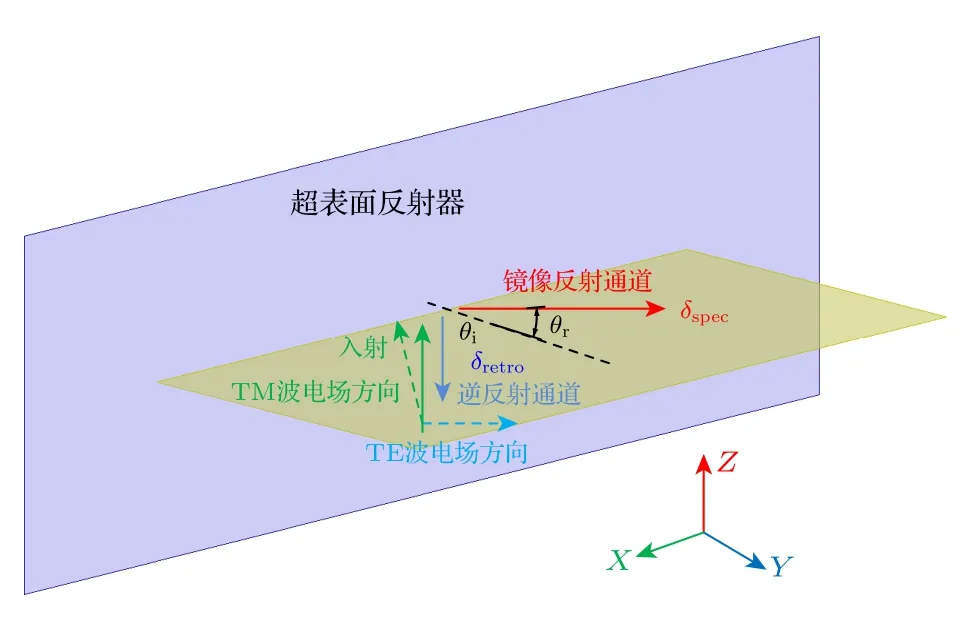
图1 介质表面镜像反射通道和逆反射通道Fig.1.Specular reflection and retroreflection of medium surface.

为在反射介质表面获取相位梯度,引入周期性梯度电磁超表面,周期内相邻子域沿反射表面切向等间隔排列,为简化设计,设相位仅沿x方向线性变化,无z向相位梯度,则ϕx=2πx/(2d),为使超表面的响应中包含逆反射通道,(2)式应存在满足θi=-θr的解,超胞在尺寸满足下式情况下包含逆反射通道,即: 2d=λ0/sinθi.进一步,设单周期内波数满足条件kg=2π/d=2k0sinθi,则为包含逆反射通道,单周期内仅需包含最小相位梯度单元数N为

当入射角θi≥19.5°,N=2条件下超表面可包含逆反射通道,即单周期内包含2个离散子结构单位.为简化设计,在满足超胞产生双通道反射的尺寸限定下,考虑以包含2个子结构的超胞进行双通道反射器设计.

由(2)式可知,逆反射超表面的工作频率严重依赖于阵列超胞尺寸,所产生响应相位及阻抗在满足波长与超胞尺寸关系下可严格获取所需最优反射特征.工作频率的偏移破坏原有相位梯度,使所需反射特征有一定偏差,两向辐射功率占比发生改变,一定的辐射特性容错率下超表面具有一定的工作带宽.

在所提超胞尺寸限定下,通过调整超表面特性实现对镜像反射通道的反射占比δspec和逆反射通道反射占比δretro的控制.以贴附金属微结构的介质板为超表面实现基体,如图2(a)所示,包含平面介质基板、基板后侧满铺的接地导体层和基板前侧二维导体微结构阵列.取单周期超胞为设计对象,超胞尺寸设为 2d×d,以二维周期排列,超胞是具有满足一定相位及反射阻抗分布的微结构,图2(b),(c)为超胞二维周期阵列及超胞微结构.为实现针对特定频率、特定入射角的具有特定反射功率比的双通道反射超表面,对超胞微结构进行优化设计.

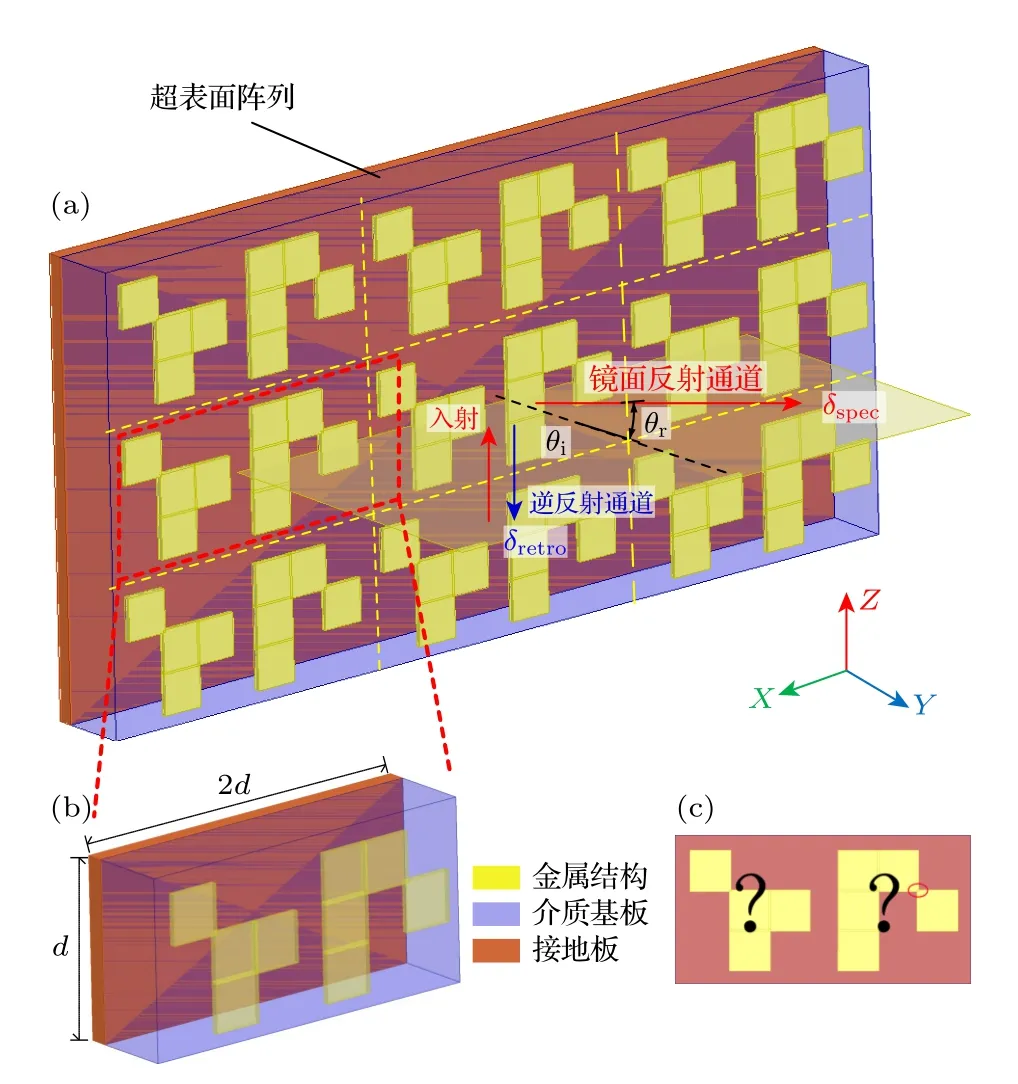
图2 双通道超表面阵列及超胞 (a) 平面型二维超表面阵列;(b) 超表面超胞;(c) 超表面超胞结构Fig.2.Double-channel metasurface array and super unit:(a) 2D planar metasurface array;(b) metasurface super unit;(c) the microstructure of the super unit.

将超胞内正面覆金属区域作为设计域进行微结构设计,该设计域为规则矩形设计域,将其划分为离散的周期矩形网格阵列,网格内帖附金属贴片或为空,网格内为空时仅为基板表面,网格内贴片的有无由一维二进制向量X表示,X=(x1,x2,x3,···,xn)T.xi=1 代表网格内存在金属贴片,xi=0代表空,以X为设计变量进行优化设计,即对设计域网格内贴片排布组合进行设计.为保证相邻网格内贴片的连接性,设置网格内金属贴片尺寸略大于网格尺寸,相邻贴片的连接性如图2(c)中红圈圈出位置所示.

对超胞内金属网格贴片分布进行优化设计以获取合理的超胞微结构.超胞在所给定尺寸下可实现包括镜像反射通道、逆反射通道、奇异反射通道在内的多通道反射,对两通道反射功率建立相应系数方程.通过数值方法计算超表面阵列远场散射特性(双站雷达散射截面积,radar cross section,即双站RCS),所扫描俯仰角θ向双站RCS为D(X;θ).提取镜像反射方向(即θr方向)和逆反射方向(即-θi方向)双站RCS数值,分别设置为D(X;θr) 和D(X;-θi),为获取特定双通道功率比,以加权双通道RCS差值最小为设计目标,设两通道功率权值分别为α和β,同时约束逆反射功率占各俯仰向扫描角度反射总功率比值大于限定阈值T,则优化列式表示为

其中,θ为俯仰角向扫描角度,θU和θL分别为扫描角度上下限.在此基础上,若需反射通道尽量由逆反射占据,可以逆反射通道(单一逆反射角度下)功率占各角度总反射功率比值(即逆反射占比)最大为设计目标,优化列式可调整为

拓扑优化流程图见图3.使用遗传算法作为优化问题的求解算法,设定优化参数,包括种群规模m、交叉及变异率,个体基因序列长度为设计变量规模n,随机生成初始种群,比较获取该种群中最优个体,即∃Xopt_1∈{Xi_1,i=[0,m]},在本代种群中设计目标最优.以本代最优设计变量作为下一代种群父本,通过交叉、变异生成新生种群,求解模型并计算设计目标,进入迭代循环,规定代数内无更优个体,则迭代停止,以当前最优个体作为最优设计变量.通过数值方法(包括商用有限元软件)计算求解超表面远场散射特性,由Matlab软件调用并提取设计目标、控制迭代及优化过程.基于前述实现机理所设计的超表面针对TE及TM波均适用(TE与TM模下电场强度方向如图1所示),但单一微结构构型并非针对两种入射波均可同时实现逆反射通道,若需要同时实现两种入射模态的逆反射通道,可在所提单目标优化设计基础上作进一步延展.

3 数值算例设计

针对包含逆反射及镜像反射的双通道超平面,所提拓扑优化设计方法为一种一般性方法,在可达到的工艺水平下受工作频率限制有限.为验证所提方法的可行性,对特定入射频率及入射角度下双通道超表面反射器进行数值算例设计及验证.选择FR4作为超表面介质基板,基板厚度1.5 mm.基板上下两侧金属均为铜,铜层厚度0.02 mm.选取TE模入射波频率为10 GHz,垂直极化电磁波以θi=-30°俯仰角斜射向超表面.计算可得超胞宽度为2d=λ0/sinθi=30mm,超胞尺寸2d×d=30mm×15 mm,超胞内各单胞设计域为12 mm×12 mm,各单胞设计域离散为 12×12 网格,尺寸为1 mm×1 mm,各贴片尺寸为1.2 mm×1.2 mm.

3.1 两通道反射功率1∶1反射器

该算例中,所需超表面反射器在±30°方向具有最大反射功率,希望对超表面进行设计以在±30°方向逆反射与镜像反射通道反射功率比为1∶1.对超表面反射器超胞微结构进行拓扑优化设计,优化列式如(4)式,模型的数值分析过程由Ansys HFSS全波模拟实现.在反射特性分析中,包围阵列空气盒子所贴附边界为完美匹配层,入射波为平面波激励,超表面阵列内超胞数量为4×6,对其归一化双站RCS进行计算.使用遗传算法优化过程中,种群规模设置为包含100个个体,交叉率0.5,变异率0.04,6代及以上种群未有更优个体产生则迭代停止.经迭代优化后,最终所设计超胞微结构如图4(a),(b)所示.计算所得其归一化双站RCS见图4(c),反射器严格在俯仰角-30°方向与30°方向表现出高反射性,两方向反射幅值大小相等,由三维辐射方向图4(d)可见其波束较窄,在±30°方向表现出较强的方向性.

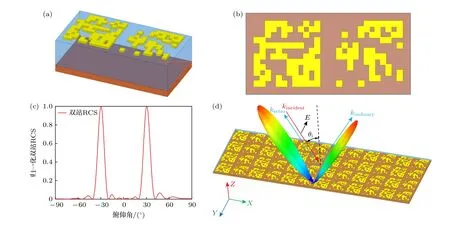
图4 所设计双通道反射功率1∶1超表面反射器及反射特性 (a) 超胞;(b) 微结构;(c) 反射器俯仰向归一化双站RCS;(d) 三维双站RCSFig.4.Designed double-channel metasurface reflector with a 1∶1 ratio of retroreflection power to specular reflection power and its reflection characteristics: (a) The unit cell;(b) the microstructure;(c) the normalized bistatic RCS in the elevation coordinate;(d) the three-dimensional bistatic RCS of the designed reflector.

仍以10 GHz及俯仰角-30°TE波照射全金属反射器,对其反射特性进行计算.由图5表明,该反射器仅在30°方向具有常规的镜像反射,无法产生逆反射通道.同时,需要强调的是,使用常规结构实现逆反射通道是较困难的,而获取包含逆反射通道的双通道反射并且反射功率占比可控的反射器同样具有一定的难度.在满足单胞尺寸范围的前提下,通过寻优可以寻到的反射器微结构形式数量十分有限,并非任意的微结构形式均可产生逆反射.

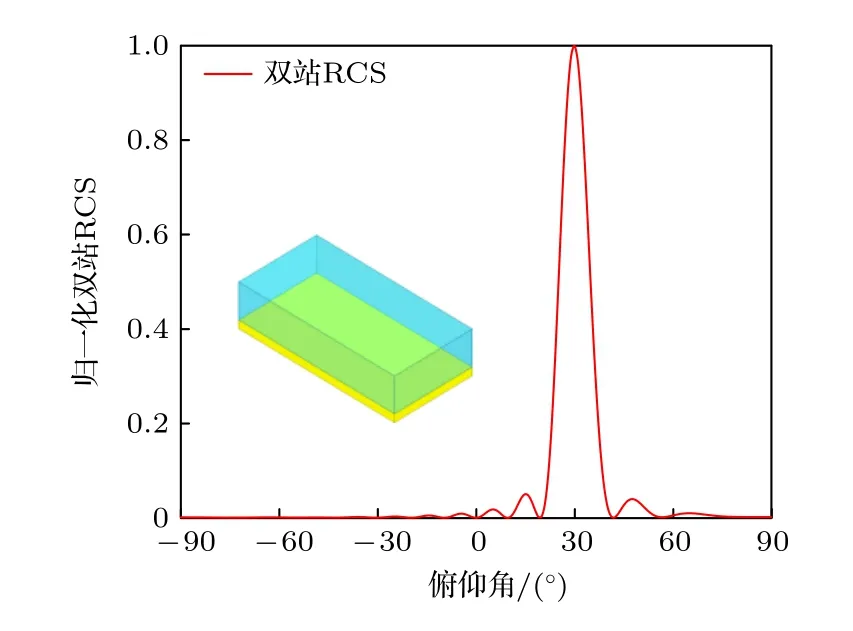
图5 仅金属接地板归一化双站RCSFig.5.Normalized bistatic RCS of the reflector only with metallic ground.

对所设计超表面进行实验测试验证,实验平台示意图如图6(a)所示.将超表面测试试件水平放置,一个喇叭天线作为发射天线固定在一端所需入射角度的摇臂上,另一个天线作为接收天线固定在旋转摇臂,用于测试各反射角度下超表面反射效率,两个喇叭天线通过同轴线与矢量网络分析仪(vector network analyzer,VNA)连接,通过对所需频点双端口S21参数的读取得到角度扫描下的反射特性.所制备超表面试件如图6(b)所示,采用覆铜板刻蚀工艺制备,试件尺寸300 mm×300 mm,二维阵列中包含10×10个超胞.以最大反射功率进行散射参数归一化,测试结果如图6(c) 所示,反射器在-28°和28°方向上反射最大,幅值近似相等,在±30°方向归一化双站RCS幅值高于0.90,测试结果与仿真结果基本接近.所测最大幅值方向较所需方向相差2°,主要误差来源包括制备误差、平台及试件放置误差.

图6 双通道超表面实验测试平台及结果 (a) RCS测试示意图;(b) 所设计超表面试件;(c)测试所得反射特性Fig.6.Experimental platform for the double-channel metasurface reflector testing and the tested results: (a) The schematic diagram of the RCS testing platform;(b) the designed metasurface specimen;(c) the tested reflection characteristics.

讨论入射角度及频率偏差下超表面反射特性.首先对入射波的入射角(俯仰角向角度)偏差所产生的反射特性的影响进行分析.保持方位角0°不变,调整入射角由-30°至-20°.入射角偏移情况下超表面不再发生逆反射,而是在入射角度负方向发生反射,反射角与入射角居于超表面法线同侧但夹角不等大,θi≠-θr,即负反射.负反射及镜像反射方向均向低数值角度方向偏转,分别偏转至-40°和20°.调整入射角由-30°至-40°,则负反射及镜像反射方向均向高角度方向偏转,分别偏转至-20°和40°,而负反射(峰值)与镜像反射通道内幅值比值保持较稳定状态.对入射波工作频率偏差对反射特性的影响进行分析,如图7所示.设定若幅值容错(幅值差值)在±0.50,则超表面工作频率在9.7—10.5 GHz,带宽0.8 GHz,此时两通道反射角分别漂移至-32°和-26°,如图8所示.

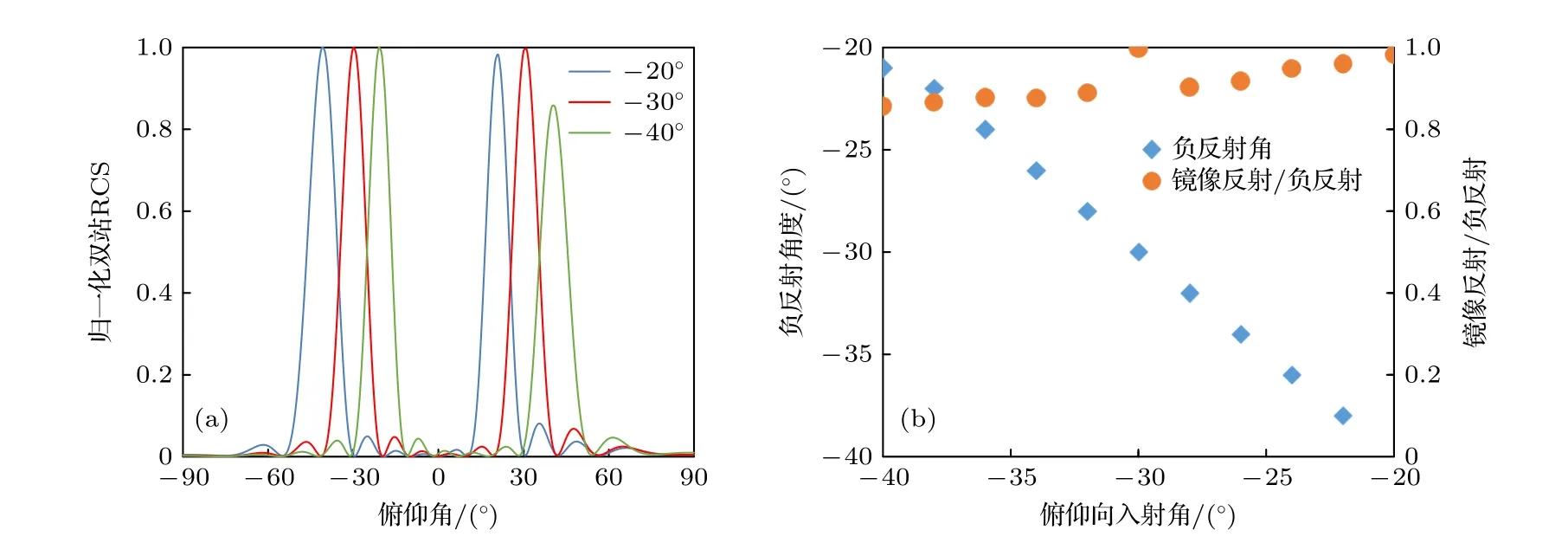
图7 入射角度偏差下的反射功率1∶1超表面反射特性 (a) 归一化双站RCS;(b) 负反射角度及镜像反射与负反射幅值比Fig.7.Reflection characteristics of the metasurface with a 1∶1 ratio of retroreflection power to specular reflection power when the incident angle is adjusted: (a) The normalized bistatic RCS of the metasurface;(b) the retroreflection angle and ratio between the specular reflection and retroreflection.

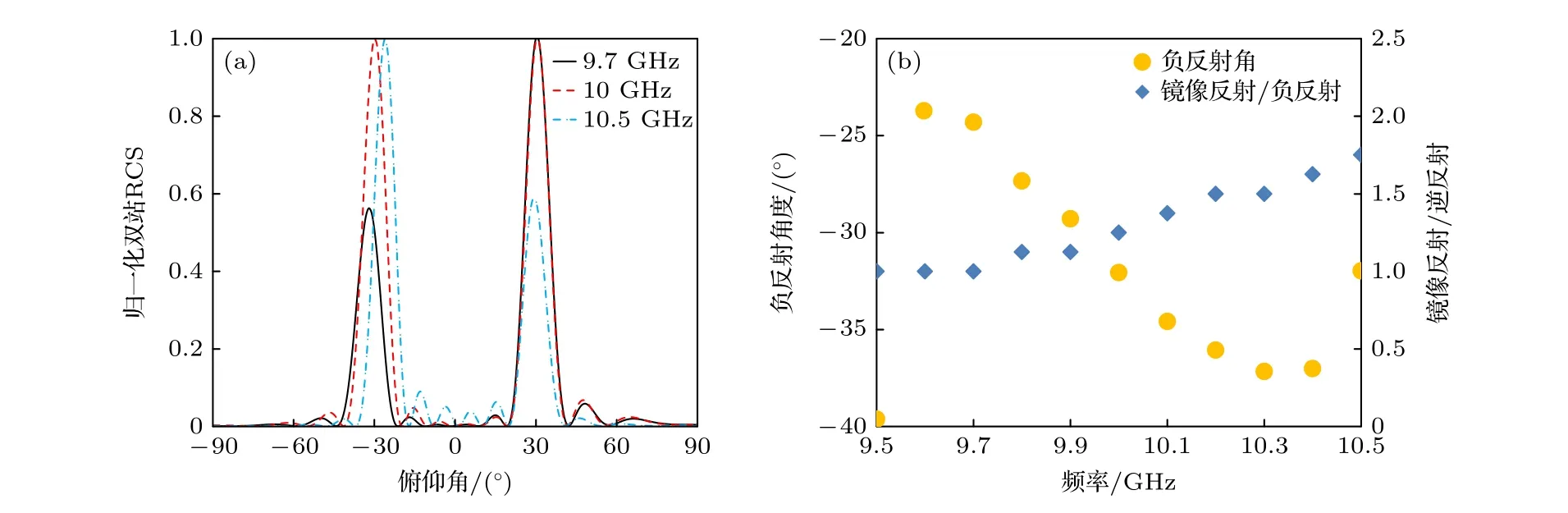
图8 入射波频率偏差下的反射功率1∶1超表面反射特性 (a) 归一化双站RCS;(b) 负反射角度及镜像反射与负反射幅值比Fig.8.Reflection characteristics of the metasurface with a 1∶1 ratio of retroreflection power to specular reflection power when the frequency of the incident wave is biased: (a) The normalized bistatic RCS of the designed metasurface;(b) the retroreflection angle and the ratio between the specular reflection and retroreflection.

3.2 逆反射占比最大反射器

为验证所提方法的通用性,对两通道具有不同反射功率占比的超材料微结构进行设计,该算例给出一种特殊设计需求,即双通道中具有最大逆反射占比,同样以-30°为入射波照射方向,超表面反射器要求在-30°方向具有最大反射功率.优化列式如(5)式,拓扑优化所设计超胞微结构如图9(a),(b).计算所得其归一化双站RCS如图9(c)所示,反射器在-30°方向具有最大反射幅值,逆反射功率占总功率比值(即-30°方向反射功率占总反射功率比值)F(S;π/6)=0.093,第一旁瓣在-15°方向最大幅值为0.006.超表面阵列使入射平面波沿初始入射方向发生反射,无镜像反射及其他方向奇异反射,半功率波束宽度10°.主波束功率占总反射功率比为0.900.实验试件尺寸参数与前述相同,实验测试所得辐射特征表明超表面强反射集中在-30°,其他方向具有极低反射功率,见图9(d).

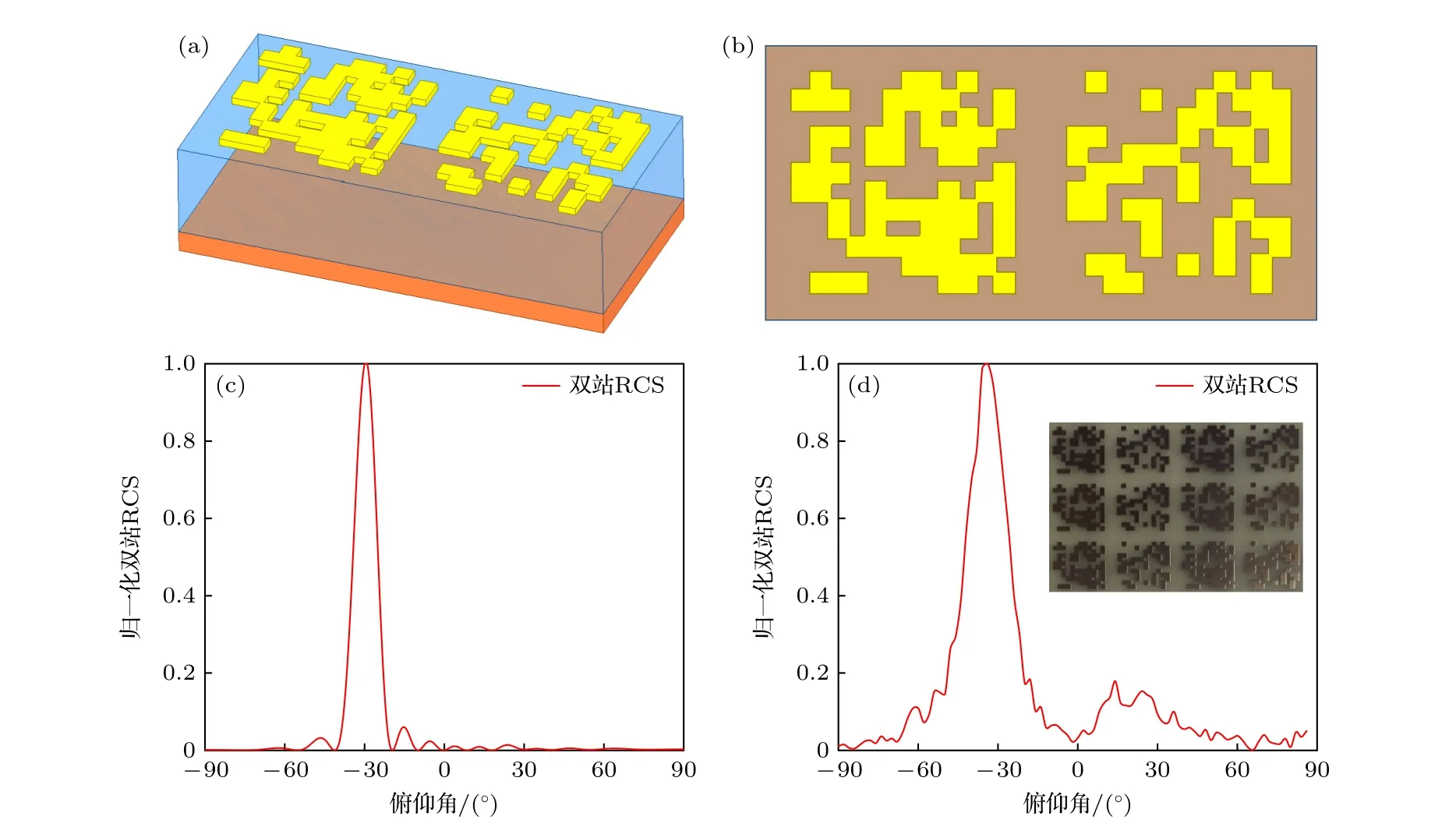
图9 所设计的逆反射占比最大超表面反射器及反射特性 (a) 超胞;(b) 微结构;(c) 俯仰向归一化双站RCS;(d) 测试所得反射特性及所设计超表面试件Fig.9.Designed metasurface reflector with the maximum retroreflection ratio and its reflection characteristics: (a) The unit cell;(b) the microstructure;(c) the normalized bistatic RCS in the elevation coordinate;(d) the tested radiation pattern and the metasurface retroreflector prototype.

分析俯仰向入射角度偏差下超表面负反射角度和逆反射占比的变化,仿真计算所得结果如图10.调整入射角由-40°至-20°,入射波方向在-26°至-34°变化过程中,逆反射占比始终高于0.05,所设计反射器表现出了一定的入射角度容错性.分析入射波频率偏差对超表面反射特性影响,所分析频率范围在9—11 GHz,如图11所示.当频率高于10.4 GHz,负反射即消失,当入射波频率由9 GHz升至10.4 GHz过程中,主波束方向逐渐由-38° 漂移至 -27°,逆反射占比在9.4 GHz升至10.2 GHz范围内始终高于0.05.

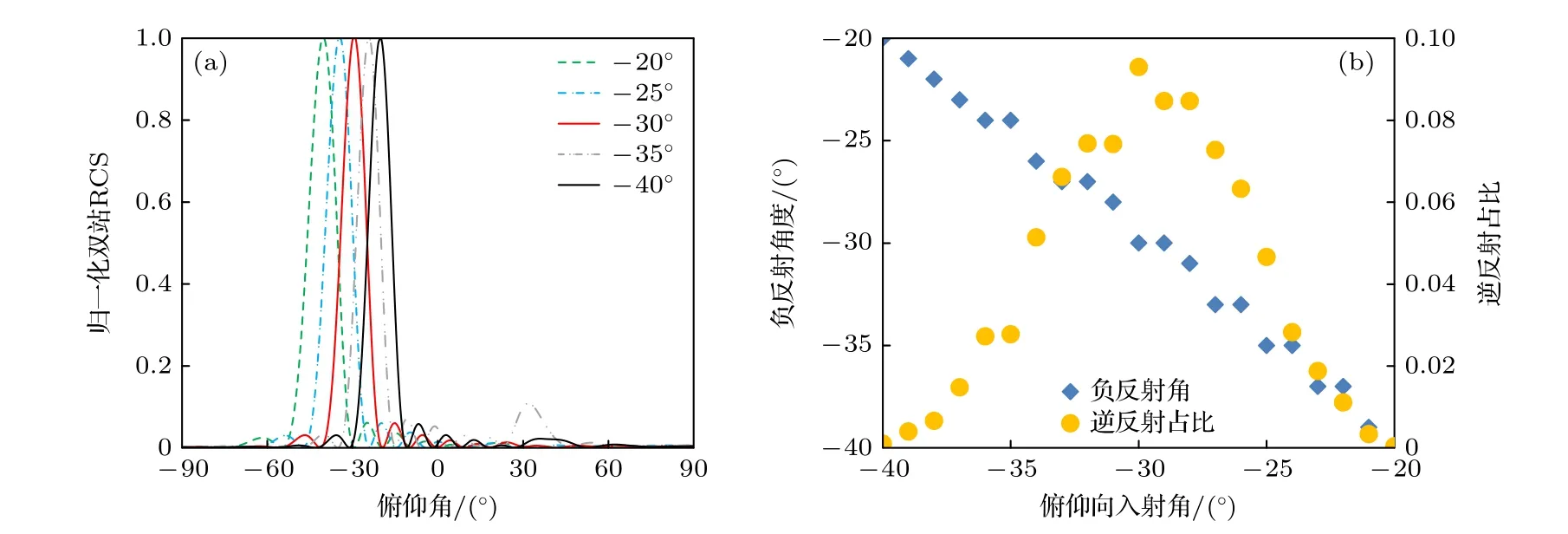
图10 入射角度偏差下的逆反射占比最大超表面反射特性 (a) 归一化双站RCS;(b) 负反射角度及逆反射功率占比Fig.10.Reflection characteristics of the metasurface with the maximum retroreflection ratio when the incident angle is adjusted:(a) The normalized bistatic RCS of the metasurface;(b) the retroreflection angle and retroreflection ratio under excitation of incident waves with different incident angle.

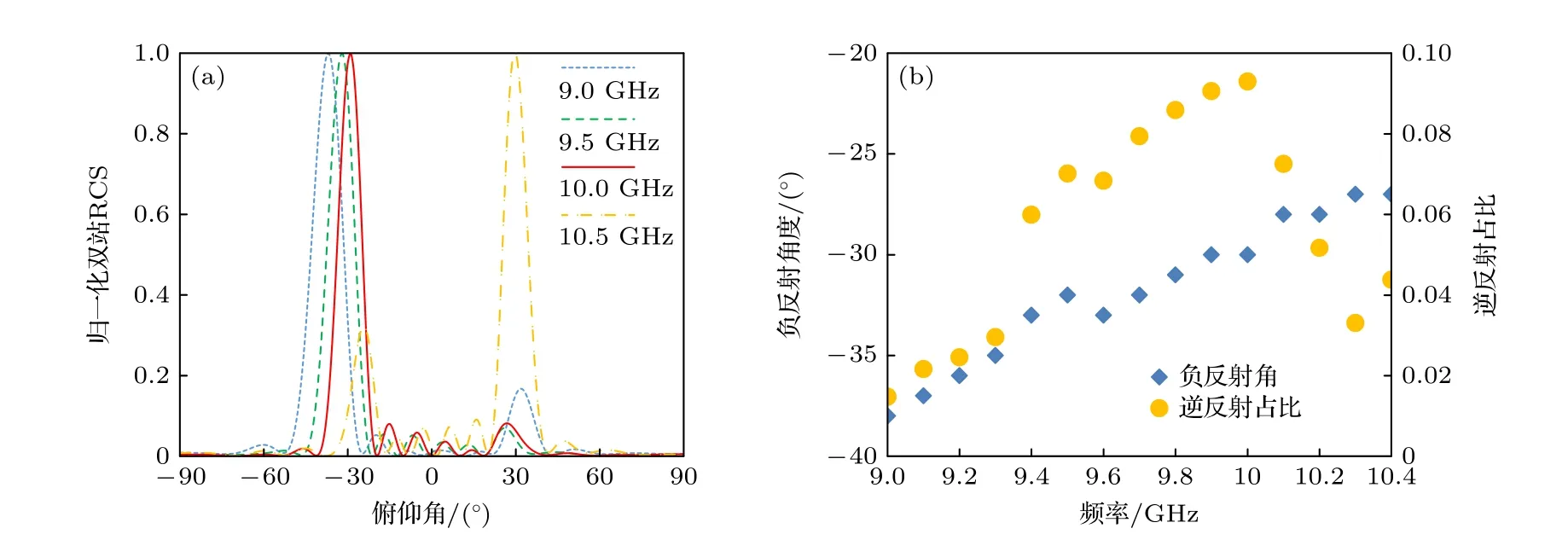
图11 入射波频率偏差下的逆反射占比最大超表面反射特性 (a) 归一化双站RCS;(b) 负反射角度及逆反射功率占比Fig.11.Reflection characteristics of the metasurface with the maximum retroreflection ratio when the frequency of the incident wave is biased: (a) The normalized bistatic RCS of the designed metasurface;(b) the retroreflection angle and retroreflection ratio under excitation of incident waves with different frequencies.

4 结论

本文提出了一种用以实现双通道反射的超表面实现形式,双通道反射可同时包含镜像反射及逆反射.建立了针对特定频率及斜入射角度入射波的双通道反射功率占比可控的超表面微结构拓扑优化方法,搭建了双通道超表面微结构拓扑优化模型.针对10 GHz入射角度-30°入射波,分别以镜像反射与逆反射权值1∶1、具有最大逆反射占比的反射器为例,对两种超表面阵列形式及微结构进行设计,所得超表面可满足两通道反射功率占比要求,仿真及实验结果验证了所提方法的可行性.