一维超导微波腔晶格中反旋波效应对拓扑相变和拓扑量子态的调制*
2024-01-06郑智勇陈立杰向吕王鹤王一平
郑智勇 陈立杰 向吕 王鹤 王一平
(西北农林科技大学理学院,杨凌 712100)
1 引言
近年来,拓扑绝缘体结构基于其独特的优势(如物理性质和化学性质),已经在不同领域展现出极其的重要性,更为凝聚态物理的研究开辟了 一个崭新的平台[1-3].不同于普通绝缘体,拓扑绝缘体是一种全新的物质形式,其内部可以展现绝缘体性质,但在边界处可以呈现出金属特性[4,5];在能带间隙中存在边缘态,不仅受到能隙的保护,而且受到时间反演对称性的制约;系统中无序和缺陷以及操纵带来的扰动,边缘态对它们都具有鲁棒性[6-9].目前,在原子、分子、光学物理和材料物理与化学等领域,研究人员正在构建新的拓扑结构,同时也提出了许多新理论模型和实验方案,用于模拟和探索拓扑绝缘体特性,从而更深入研究其中的拓扑物态和量子物质,这已经成为一个研究热点问题[10-12].
随着微纳米器件制备工艺的成熟,进一步促进了微纳量子器件的发展,并开启了一个崭新的研究领域——微纳光子学,其主要研究在微纳尺度下光与物质相互作用的规律,以及光的产生、传输、调控、探测和传感等[13-16].例如,光学微腔系统可以将光束缚在微小的区域范围内,可以极大地增强光与物质的相互作用,并且通过制备高品质因子的光学微腔,可提高系统在传感和探测方面的灵敏度[17-22].特别地,超导微波器件能够有效提高光子集成度,进而集成在芯片上应用于量子光学、量子信息处理和量子模拟等领域,这已经成为最具吸引力的平台之一[23-29].另外,微纳米量子器件在模拟拓扑绝缘体方面已经取得了具大的突破,如超导微波腔、RLC电路、纳米机械振子、超导量子比特和NV自旋,相互耦合构建一维或二维晶格系统,并通过微波相干调控,以展示许多新奇的拓扑物理现象,如拓扑相变和边缘态、非厄米拓扑绝缘体、拓扑不变量等,来实现一些特殊功能的量子器件[30-36].例如,Koch等[37]和Mei等[38]分别利用超导微波腔构建一维晶格系统实现了拓扑Chern绝缘体,后者对系统的拓扑边缘模和不变量进行了探测;此外,Cai等[39]和Cao等[40]利用超导电路系统构建二维晶格系统,分别研究磁子绝缘态和能带结构与异常环.因此,基于之前的研究工作[33-40],本文利用超导微波腔系统构建一维的拓扑系统,考虑系统的反旋波项的效应,分析、研究和调控其中的拓扑绝缘体性质.
本文构建了基于超导微波腔的一维拓扑晶格系统,其中包含两种微波腔晶胞元素,通过磁通量子比特耦合晶胞元素,来分析和研究其中的拓扑绝缘体特性.这里保留晶格之间相互作用的反旋波项,使拓扑超导体中的p-波超导配对项与其相映射,得到具有p-波超导配对项的一维超导微波腔晶格方案.研究发现,p-波超导配对项可以调制系统中拓扑量子态,可以实现多通道的拓扑量子信息传输.此外,当考虑p-波超导配对项和次近邻相互作用时,发现能带的波动可以诱导系统产生新的能带,边缘态发生弯曲,但其简并性保持稳定,通过调制可以实现拓扑量子态不同的传输路径;然而,当调控超过阈值时,系统的能隙将会闭合,使边缘态湮灭在新的能带中.另外,考虑系统存在随机的缺陷时,发现能带呈现无规则的波动,边缘态有微小的扰动;当缺陷强度超过阈值时,能带导致强烈的无规则波动,使边缘态融入能带中.
2 系统模型及哈密顿量
如图1(a)所示的一维超导微波腔晶格系统,其中包含an和bn两种微波腔晶胞元素,并且通过两种不同类型的量子比特互相交叉耦合.此外,如图1(b)所示,an和bn微波腔晶胞耦合在一个频率可调的控制场上,其频率在ωan=ωa+λncos(υt+ϕ)和ωbn=ωb+γncos(υt+ϕ)的范围内调制,ωa和ωb是微波腔晶胞的固有频率,λn(γn) 是微波腔晶胞的频率调制强度,υ描述微波腔晶胞的调制频率,ϕ是相位因子.因此,该一维晶格电路系统的哈密顿量可以写成

图1 (a)基于超导微波腔组成的一维晶格系统,Q1 (Q2)是晶胞之间的耦合磁通量子比特,g1 (g2)表示 an (bn)和 bn (an+1)的耦合参数,T表 示 an和an+1 (bn和bn+1)的耦合参数;(b) an和bn 耦合在一个频率可调的控制场上,g1 (g2) 可以通过磁通量子比特外部磁通调控,T通过电容C耦合调制Fig.1.(a) Schematic of the 1D superconducting microwave cavity lattice system,Q1 (Q2) is the coupling flux qubit between the unit cell,an and bn (bn and an+1) coupling coefficient is g1 (g2),an and an+1 (bn and bn+1) coupling coefficient is T;(b) an and bn are connected in a tunable frequency field,g1 (g2) can be modulated by the external flux of qubits,T is modulated by the capacitance C coupling.
其中,ω1±=(ωa±ωb)t+(λn±γn)sin(υt+ϕ),ω2±=(ωa±ωb)t+(λn+1±γn)sin(υt+ϕ),第1项和第3项为最近邻微波腔晶胞间耦合的反旋波项,第2项和第4项为微波腔晶胞间最近邻耦合.这里,先不考虑次近邻作用,即T=0,研究系统中的反旋波项在晶格电路系统中的作用.利用exp[iKsin(υt)]=为关于贝塞尔函数的m次序),使相位ϕ=0,对哈密顿量H1展开,(2)式可以写成:
其中,G11=g1Jm1(K1,n),G12=g1Jm2(K2,n),G23=g2Jm3(K3,n),G24=g2Jm4(K4,n),K1,n=λn+γn,K2,n=λn-γn,K3,n=λn+1+γn,K4,n=λn+1-γn.当系统在共振条件下ωa=ωb=υ,λn+1=γn=λn,取m1=m3=-2,m2=m4=0 时,m1(m2,m3,m4) 求和项和(3)式中的e指数项可以忽略,哈密顿量H2描述为
3 结果与讨论
3.1 反旋波项调制
在拓扑绝缘体中,p-波超导配对项的存在能够诱导许多新奇的物理现象.这里考虑频率调控的方法,使一维晶格电路的反旋波项与p-波超导配对项关联,通过调控反旋波项,从而得到带有p-波超导配对项的一维拓扑电路晶格系统,这为探索丰富的拓扑特性和相变提供一种新思路.首先,考虑没反旋波项的调制,即通过贝塞尔函数来调控p-波超导配对项的强度为零,那么哈密顿量H3可以简化,从而得到一个标准的一维拓扑紧束缚模型,对应的哈密顿量为H4=因此,根据上述哈密顿量H4,可以绘制系统的能谱图,来研究和分析其中拓扑边缘态的概率分布.在这里,定义蓝色和红色边缘态的概率分布,即 ||ψblue〉|2和||ψred〉|2,相对应的能量本征值为Eblue和Ered.图2给出了系统的能谱和边缘态与晶格数目的关系.如图2(a)所示,能谱有δE的能带间隙,并且存在两个简并的边缘态.图2(b)和图2(c)展示了边缘态(第50 (蓝色)和第51(红色))的概率分布,可以清楚地看到边缘态分布在一维拓扑晶格电路系统的两端.

图2 (a)系统能谱与晶格数目的关系;(b)蓝色和(c)红色边缘态的概率分布图;其中 =0.15,=0.3 和晶格数N=100Fig.2.(a) Energy spectrum of the system via the lattice numbers;(b),(c) probability distributions of (b) blue and (c) red edge states.=0.15,=0.3 and lattice size N=100.

图3 系统能谱与晶格数目的关系 (a) ==0.003;(b) ==0.03;(c) ==0.06;(d) ==0.15;(e) ==0.165;(f) ==2.1;其他参数为 =0.15,=0.3 和晶格数N=200Fig.3.Energy spectrum of the system via the lattice numbers: (a) ==0.003;(b) ==0.03;(c) ==0.06;(d) ==0.15;(e) ==0.165;(f) ==2.1.Other parameters are =0.15,=0.3 and lattice size N=200.
此外,如图4所示,我们分析了系统4个简并边缘态的概率分布.从图4(a)和图4(b)可以清楚地看到,当逐渐增加p-波超导配对项耦合强度时,红色边缘态的分布发生了翻转过程,也就是说,红色边缘态从系统最左边传递到腔的最右边.与图4(a)和图4(b)对比,从图4(c)可以看到,红色边缘态分布在系统的两端,通过调控p-波超导配对项耦合强度,可以使边缘态分布在右端(图4(d))或者左端(图4(e)).另外,从图4 中观察到其他3个边缘态(蓝、黑、绿),在系统中分布的位置各有差异,那么通过调制p-波超导配对项耦合强度,在系统中可以实现多路径的拓扑量子信息传输.
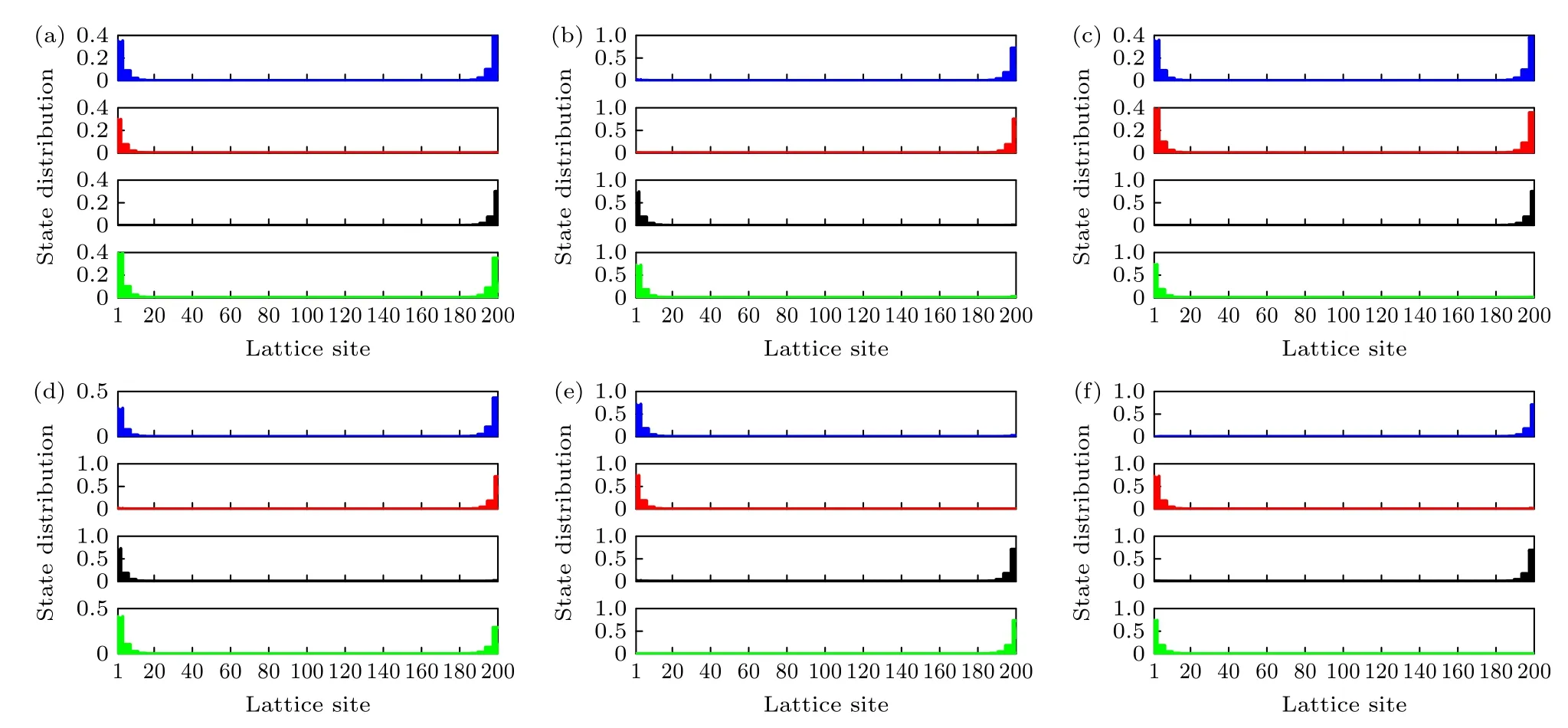
图4 4个不同边缘态的概率分布图 (a) ==0.003;(b) ==0.006;(c) ==0.009;(d) ==0.015;(e) ==0.021;(f) ==0.027;其他参数为 =0.15,=0.3 和晶格数 N=200Fig.4.State distributions of four different edge states: (a) ==0.003;(b) ==0.006;(c) ==0.009;(d) ==0.015;(e) ==0.021;(f) ==0.027.Other parameters are =0.15,=0.3 and lattice size N=200.
3.2 次近邻相互作用
在一维拓扑晶格电路的结构中,通过调控晶格之间的相互作用,可以研究和探索其中许多有趣的拓扑现象.接下来考虑p-波超导配对项和次近邻相互作用对系统拓扑性质的影响,系统的哈密顿量可表示为
其中,T0=TJ0(K2,n) 用来描述一维拓扑晶格电路系统中次近邻相互作用.根据(5)式中的次临近相互作用和p-波超导配对项,进一步研究和分析两者对系统的拓扑性质的影响.这里考虑其周期调控,即参数为T0=Tcosθ和==0.08(1+cosθ),通过分析能谱结构的变化特征,研究系统的拓扑相变和拓扑通道.
图5(a)给出了次近邻相互作用T=0 时系统能谱与相位的关系,可以清楚地看到能带中存在4个简并的零模边缘态(蓝色),它们分别和上下能带存在间隙,类似于图3(a).然而,当T=0.05 时,系统的上下能带发生波动,并引起4个边缘态起伏,但简并度没有发生变化,例如,在θ∈[0.5π,1.5π]位置有4个边缘态(蓝色)凸起,在θ∈[0,0.5π] 和θ∈[1.5π,2π]位置有4个边缘态下降.由上述分析可知,当p-波超导配对项调制恒定时,周期调制次临近相互作用可引起能带和边缘态的周期起伏变化.如图5(c)所示,当T=0 时,周期调制p-波超导配对项,即==0.08(1+cosθ),可以看到系统上下能带变化不同于图5(b),4个简并边缘态(蓝色)保持稳定.从上面的讨论分析可以发现,它们对系统的拓扑能带结构调制不同,也就是说,这两者的变化可以导致系统进入不同的拓扑相中.

图5 系统能谱与相位的关系 (a) ==0.1,T=0;(b) ==0.1,T=0.05;(c) ==0.08(1+cosθ),T=0;其他参数为 =0.2,=0.4 和晶格数N=200Fig.5.Energy spectrum of the system via the phase:(a) ==0.1,T=0;(b) ==0.1,T=0.05;(c) ==0.08(1+cosθ),T=0.Other parameters are =0.2,=0.4 and lattice size N=200.
为了进一步深入探索其中的拓扑特征,图6给出了不同p-波超导配对项调制系统的能谱图.从图6(a)和图6(b)可以发现,p-波超导配对项调制强度不断增加时,系统的能带间隙将逐渐变小,并且能带结构发生变化,使上下能带产生新的能带,但4个边缘态依然保持简并,并且在一个稳定的状态,没有发生混乱.然而,从图6(c)清楚地看到,当p-波超导配对项调制强度达到一定值时,部分边缘态融入到新的能带中,而另一部分边缘态保留在θ∈[0.25π,0.75π]和θ∈[1.25π,1.75π] 区域的能隙中.如图6(d)所示,当p-波超导配对项调制强度超过阈值时,上下能带产生的新能带使边缘态全部湮灭在其中,进入另一个拓扑相.

图6 系统能谱与相位的关系 (a) ==0.08;(b) ==0.16;(c) ==0.24;(d) ==0.32;其他参数为 =0.2,=0.4,T=0.1 和晶格数N=200Fig.6.Energy spectrum of the system via the phase: (a) ==0.08;(b) ==0.16;(c) ==0.24;(d) ==0.32.Other parameters are =0.2,=0.4,T=0.1 and lattice size N=200.
此外,当p-波超导配对项的调制恒定时,通过周期性调控次近邻相互作用,分析其对系统的拓扑特征的影响.如图7(a)和图7(b)所示,当次近邻相互作用T逐渐增加时,能带和边缘态结构发生变化,比如在θ=π 位置上下能带发生重叠,部分边缘态湮灭在重叠区域.然而,从图7(c)和图7(d)可以发现,当T增加到一定时,上下能带将全部重合,边缘态将融入能带中.

图7 系统能谱与相位的关系(a)T=0.1;(b) T=0.2;(c) T=0.3;(d) T=3;其他参数为=0.2,=0.4,==0.04 和晶格数N=200Fig.7.Energy spectrum of the system via the phase: (a) T=0.1;(b) T=0.2;(c) T=0.3;(d) T=3.Other parameters are=0.2,=0.4,==0.04 and lattice size N=200.
根据前面的讨论,p-波超导配对项和次近邻相互作用的调控,可以会引起能带的波动,但4个边缘态的简并性一直保持稳定,并且没有发生混乱和扰动,那么可以利用边缘态的拓扑特性,在系统中进行量子信息的传输和储存操作.图8绘制了不同相位θ下4个边缘态的概率密度分布图,对其中的拓扑量子通道进行分析和研究.从图8(a)和图8(b)可以发现,当θ=π/2 时,对p-波超导配对项调控的耦合强度进行调制,4个边缘态可以分别从系统的一端转移到另一端,比如蓝色的边缘态分布在最右边的位置(图8(a1)),通过耦合强度调制后,蓝色的边缘态分布在最左边的位置(图8(b1)).因此,通过调控和大小,可以使系统的边缘态分布呈现一个翻转过程,这可以应用于量子信息的传输通道.
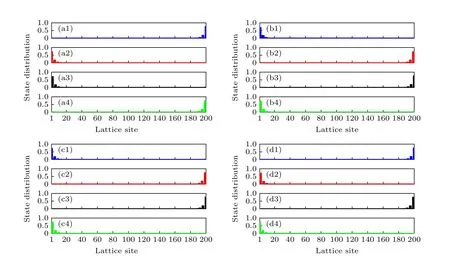
图8 4个不同边缘态的分布图 (a) θ=π/2,==0.08;(b) θ=π/2,==0.1;(c) θ=3π/2,==0.08;(d) θ=3π/2,==0.1.其他参数为 T=0.1,=0.2,=0.4 和晶格数N=200Fig.8.State distributions of four different edge states: (a) θ=π/2,==0.08;(b) θ=π/2,==0.1;(c) θ=3π/2,==0.08;(d) θ=3π/2,==0.1.Other parameters are T=0.1,=0.2,=0.4 and lattice size N=200.
另外,从图8(a2)和图8(c2)可以看出,当θ=π/2时,红色的边缘态分布在最左边的位置;当θ=2π/3时,红色的边缘态分布在最右边的位置.可以调控相位参数θ,即调制次近邻相互作用,使系统的边缘态分布呈现一个翻转过程,也就是说,在次近邻作用下,可以实现4个不同通道的量子拓扑信息传输.此外,与图8(a)和图8(c)相比,在图8(b)和图8(d)中只有两个边缘态(蓝色和红色)展现一个翻转过程,其他两个分布位置保持不变,这源于p-波超导配对项耦合和次近邻相互作用之间潜在的相辅性,引起边缘态分布的差异性,正如图8(b)和图8(c)所示,4个边缘态的分布位置完全相同,但所使用参数不同,那么通过优化系统的参数可以实现多通道的拓扑量子信息传输.
3.3 随机缺陷的扰动
在目前的实验中,由系统涨落引起的无序以及操纵带来的微扰,这些将会影响系统拓扑性质,并且是不可回避的问题,需要深入的研究和分析.接下来,把无序和微扰看作系统的随机缺陷,进一步讨论其对系统的拓扑的影响,哈密顿量表示为
其中ω,ν和τ分别描述反旋波项、最近邻和次近邻相互作用项的随机缺陷强度,δ∈[-0.5,0.5] 是随机数.
图9绘制了不同随机缺陷下的系统能谱图.从图9(a)—(c)可以看到,在ν=τ=0 时,随着ω逐渐增加,系统的上下能带开始无规则地波动,同时4个简并的边缘态也轻微地扰动,但边缘态可以区分;然而,当ω≥0.7 时,上下能带开始重叠,导致边缘态湮灭在能带中,如图9 (d)所示.另外,如图9(e)—(g)所 示,当ω=τ=0 时,随 着ν逐 渐增加,系统的上下能带也产生无规则波动,但边缘态的扰动比图9(a)—(c)中的轻微一点,边缘态可以区分.如图9(h)所示,当ν≥0.4 时,上下能带的带隙闭合,导致边缘态湮灭在能带中,这和图9(d)所示相同.此外,从图9(a)—(h)中能带和边缘态的变化趋势可以清楚地看到,ω和ν导致的扰动各有异同,例如,能带的无规则波动和边缘态的扰动程度不同,也发现能带的无规则波动引起的带隙闭合趋势相同,其中ω值要比ν值大多.
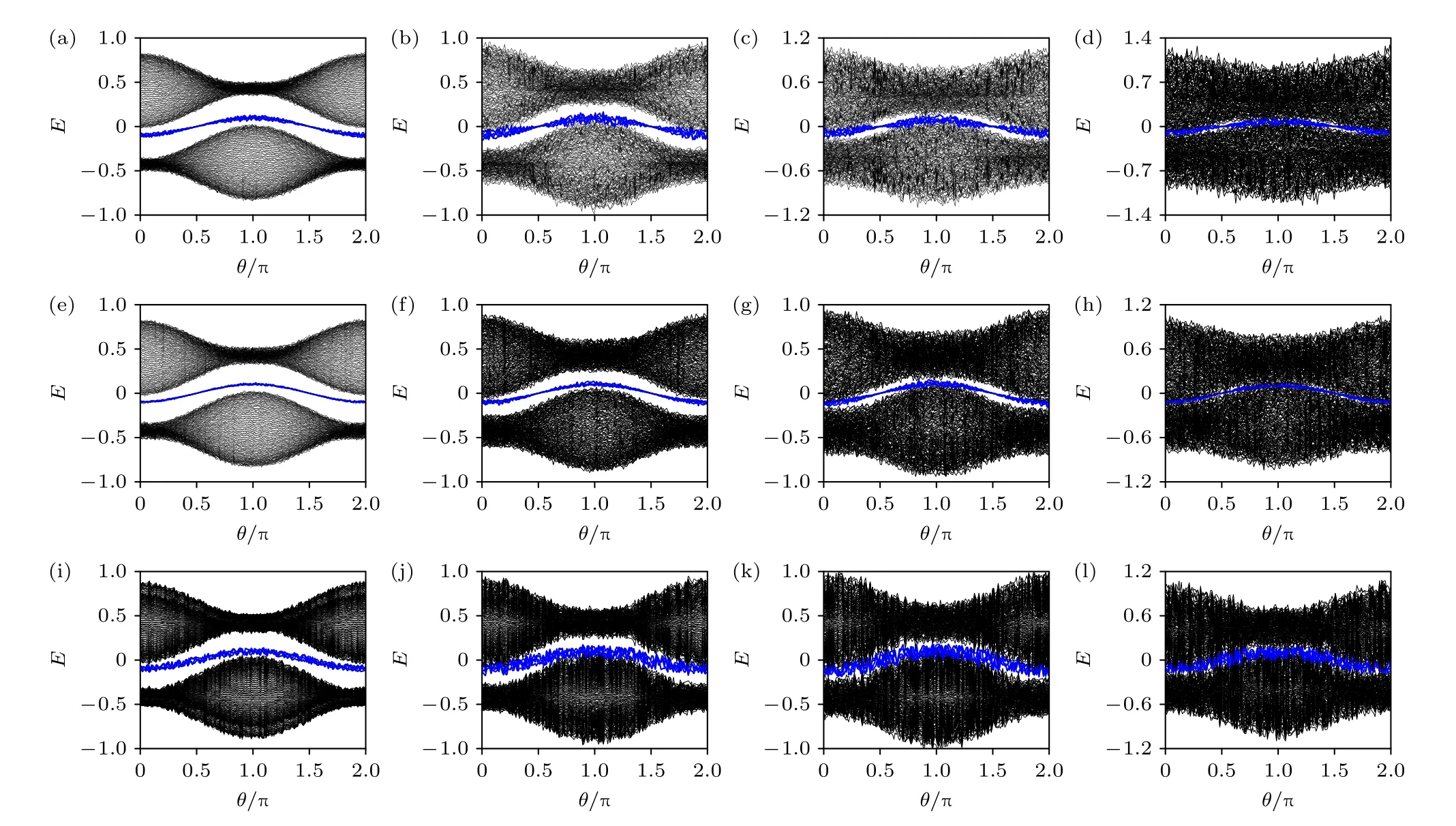
图9 系统能谱与随机缺陷的关系图 (a) ω=0.1,ν=τ=0;(b) ω=0.3,ν=τ=0;(c) ω=0.5,ν=τ=0;(d) ω=0.7,ν=τ=0;(e) ν=0.1,ω=τ=0;(f) ν=0.2,ω=τ=0;(g) ν=0.3,ω=τ=0;(h) ν=0.4,ω=τ=0;(i) τ=0.1,ω=ν=0;(j) τ=0.2,ω=ν=0;(k) τ=0.3,ω=ν=0;(l) τ=0.4,ω=ν=0;其他参数为=0.2,=0.4,==0.04,T=0.1和晶格数N=200Fig.9.Energy spectrum of the system via the random defects: (a) ω=0.1,ν=τ=0;(b) ω=0.3,ν=τ=0;(c) ω=0.5,ν=τ=0;(d) ω=0.7,ν=τ=0;(e) ν=0.1,ω=τ=0;(f) ν=0.2,ω=τ=0;(g) ν=0.3,ω=τ=0;(h) ν=0.4,ω=τ=0;(i) τ=0.1,ω=ν=0;(j) τ=0.2,ω=ν=0;(k) τ=0.3,ω=ν=0;(l) τ=0.4,ω=ν=0.Other parameters are =0.2,=0.4,==0.04,T=0.1 and lattice size N=200.
另一方面,如图9(i)—(k)所示,当ω=ν=0时,τ增加到一定程度时,可以看到上下能带逐渐闭合,边缘态将融合在能带中,但边缘态的扰动程度大于图9(a)—(h)所示;当τ≥0.4 时,上下能带的带隙闭合,边缘态在能带中湮灭,而这和图9(d)、图9(h)所示相同.根据上面的分析与讨论可以得到,系统的不同随机缺陷都会影响其能带结构特征,但较小值的缺陷对系统的边缘态扰动微小,能隙中边缘态可以区分,说明其具有鲁棒性;然而,当缺陷较大时,能带间隙闭合,边缘态将湮灭在能带中.此外还发现,三者对边缘态的扰动程度不同,次临近相互作用的缺陷对边缘态的扰动最大,最近邻相互作用的缺陷对边缘态扰动最小.因此,在实验制备和操作中,需要考虑这些缺陷引起的扰动,尽可能地调控在合适的范围,使实验结果具有建设性和应用性,进一步拓展拓扑量子信息的储存和传输方式.
4 结论
本文提出基于超导微波腔的一维晶格理论方案,通过磁通量子比特调控晶胞之间的耦合,考虑反旋波项与p-波超导配对项相映射,获得p-波超导配对项的一维晶格方案,来模拟和探索其中拓扑绝缘体特性.研究发现,通过调控p-波超导配对项,系统可以实现4个边缘态的拓扑量子信息传输通道.此外,当加入次近邻相互作用时,其可以诱导能带产生新的能带,边缘态的简并性稳定,可以实现不同路径的拓扑量子态传输;然而,当次近邻相互作用调控超过阈值时,能隙会闭合,边缘态湮灭在新的能带中.另外,当系统存在缺陷时,发现缺陷较小时,边缘态对其具有鲁棒性;当缺陷超过阈值时,能带会导致剧烈的波动,使边缘态消失.本文的研究结果具有广泛的潜在应用,对未来建立可扩展量子网络具有重要的指导性建议.
