基于Stokes矢量差分法的背景光偏振特性研究*

徐菁焓 吴国俊† 董晶 于洋 封斐1) 刘博1)

1) (中国科学院西安光学精密机械研究所,西安 710119)

2) (中国科学院大学,北京 100049)

3) (青岛海洋科技中心,青岛 266237)

1 引言

水下光学成像技术具有探测结果信息直观,分辨率高的特点,是观探海洋的重要手段.然而水体对光的散射作用使背景散射光难以和目标信息分离,严重降低水下成像质量,限制水下探测距离.因此探究水中散射光的光学特性,实现背景散射光的抑制甚至去除,提高水下图像的信噪比,是提升水下光学成像技术探测性能的重要任务.水下偏振光成像技术利用目标物信息光和背景散射光的偏振差异,可实现优于普通光学探测结果的高对比度探测,且偏振成像系统质量体积轻巧,便于搭载水下无人设备,成本低廉,已成为目前提升水下探测结果信噪比的重要方法[1-3].

背景光的偏振信息在水下偏振图像复原领域里是一项重要的参数,然而这一参数大多基于假设偏振状态,或利用一个粗略的估计值代入到成像模型中开展复原计算.Cariou等[4]通过设置参考信号光路研究含高岭土颗粒水体的散射信号,发现后向散射光通常为线偏振光,且偏振方向与入射光的偏振方向相同.Sabbah和Shashar [5]通过使用急流取样偏振仪进行水下实测分析得出,水下成像过程中后向散射光为部分偏振光.Cronin和Marshall[6]指出大多数水下散射光产生的偏振在方向上接近水平,因此使用水平偏振器拍摄的图像明显比使用垂直方向的偏振器拍摄的图像更模糊.这些对背景光偏振特性的先验性结论为基于水下物理成像模型的主被动偏振图像复原[7-10]奠定了理论基础.然而对背景散射光的偏振部分和非偏振部分进行理论化分离并不能实现对其偏振特性的定量分析.为更深入研究水中背景散射光的偏振特性,研究人员以偏振度(degree of polarization,DOP)为参量开展了背景散射光在水体中传输的模拟研究和实验研究,如基于蒙特卡罗仿真获取理论上散射光在水中传播时,其DOP随光学厚度的变化[11];研究线偏光、圆偏光在不同浑浊水体中传播时,其散射光的保偏性[12,13];定量分析前向、后向散射光在不同浊度水体中的退偏振程度[14,15]等.着眼于微观角度,孙晶华[16]模拟分析了藻类和泥沙的大小颗粒在水体中的后向散射的极化分布情况以及后向散射极化程度随浊度的变化情况;着眼于宏观角度,田恒团队[17,18]从马吕斯定律的角度出发,提出背景光偏振方向取决于其偏振度并且可由Stokes矢量估算范围,该范围为,其中P表示背景光的DOP,α表示背景光偏振角度.实际上,无论是偏振光自身在水体之中产生退偏振,还是自然光在水体中传播经多次散射后具备了偏振特性,其主要原因是原本偏振态的极化方向发生了改变.因此量化背景散射光的偏振角度变化,尤其是不同水质中的极化变化情况,是掌握背景散射光的偏振传输特性的重点,也有望实现水下探测结果的理想去散射的可行研究方向.

为了进一步探究背景散射光的偏振特性,尤其是偏振角度这一参量,本文提出了一种基于Stokes矢量差分法 (modified polarization difference imaging method,M-PDI)[17,18]的背景光偏振方向研究方法.首先量化分析M-PDI和普通差分方法(polarization difference imaging,PDI)[19]的差异.随后基于M-PDI的水下物理模型遍历寻找与偏振角度相关的最优权重系数,利用最优权重系数和偏振角的数学关系反演背景光偏振方向,获取背景散射光的确切偏振角度.最后通过改变水体浊度,分析了M-PDI对散射光的抑制极限,探究了背景散射光的偏振角度随水体浊度变化的分布规律.

2 基于M-PDI的背景光偏振方向研究

2.1 M-PDI原理

Stokes矢量用于描述光的偏振状态,表示为S=(I,Q,U,V)T,其右上角标T表示转置.I代表光的强度,Q代表0°和90°偏振方向光强差值,U代表45°和135°偏振方向光强差值,V代表右旋偏振光和左旋偏振光的强度差值.基于Stokes矢量可以计算出光场的DOP,即光束中偏振光的能量占总能量的比例,可以表示为

也可描述光束矢量振动方向,即偏振角(angle of Polarization,AOP),可以表示为

背景散射光(B)与目标信息光(T)在偏振方法中有图1所示的几何关系.P1和P2为偏振器件,β为T的偏振角,α为B的偏振角.定义经起偏器P1入射的光为I⊥,经检偏器P2出射的光为I//.当背景光的偏振方向α和相互正交的P1,P2的透射方向均成45°时,可实现背景散射光的滤除.

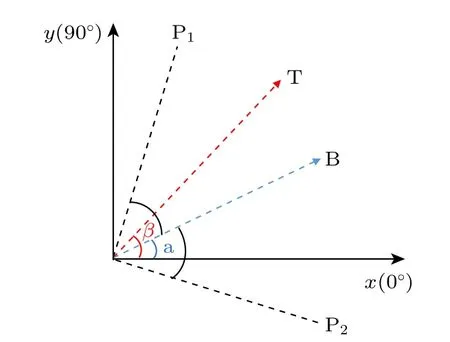
图1 偏振差分探测原理[17]Fig.1.Detection principle of polarization difference imaging[17].

T和B的Stokes矢量形式可以表达为

一般用斯托克斯-穆勒矩阵(Stokes-Muller matrix)来描述入射光与光路中物体的作用过程,能改变光偏振态的偏振器件也有着固定的穆勒矩阵表述[20].反射光携带目标物偏振信息这一物理过程可表示为

其中M表示目标物的穆勒矩阵,Sreflect和Sin分别表示反射光和入射光的偏振信息.这一物理过程具有累乘特性,当光路中存在多个物体时,最终的输出光可表示为

式中Sin表示输入光,Sout表示最终输出光,Mn表示光路内所经物体的穆勒矩阵,n表示数目.因此入射光经过相互正交的偏振器件调制后获得的输出光强将表示为

将(7)式进行差分运算可得

最终M-PDI的输出结果为

2.2 背景散射光偏振方向研究方法

为获取背景光偏振角度信息,将偏振角的定义(2)式进行变换,可得背景光有如下表达式:

同理,对目标信号光处理后可得

因此M-PDI方法可以表示为

可将(10)式写为IM-PDI=Q-γU,γ称之为权重系数.当γ=1/tan(2α) 时为M-PDI方法的最优权重系数,对应着最佳探测效果.为了确定最优权重系数的确切数值,需要对M-PDI的输出结果进行量化描述,本方法选取图像增强测度[21](enhancement measure evaluation,EME)作为量化标准.EME是描述图像清晰度变化的重要指标,其数学表达为

式中,x,y为像素的坐标值,其原理为把图像分为k1×k2块小区域(l和k为行列编号),计算出小区域中灰度最大值和最小值的对数均值,表现的是图像局部域灰度的变化程度.局部灰度变化越强,图像表现出的细节就越强.

首先将Stokes矢量图像Q和U代入M-PDI模型中,然后将模型输出结果IM-PDI的EME最大设为最优判断指标,以此对权重系数γ进行最优值搜寻.在线偏振光入射情况下,权重系数范围为(0,1),因此设置0.01为搜索步长寻找EME最高时的权重系数.完成遍历流程即可确定最优权重系数.随后根据γ=1/tan(2α) 对最优权重系数取反,获得此时背景光偏振方向角α.上述方法整体流程如图2所示.最后将不同浊度条件下的Stokes矢量图像Qi和Ui(i=n)代入上述方法,研究背景光偏振方向角度随水体浊度变化的趋势.

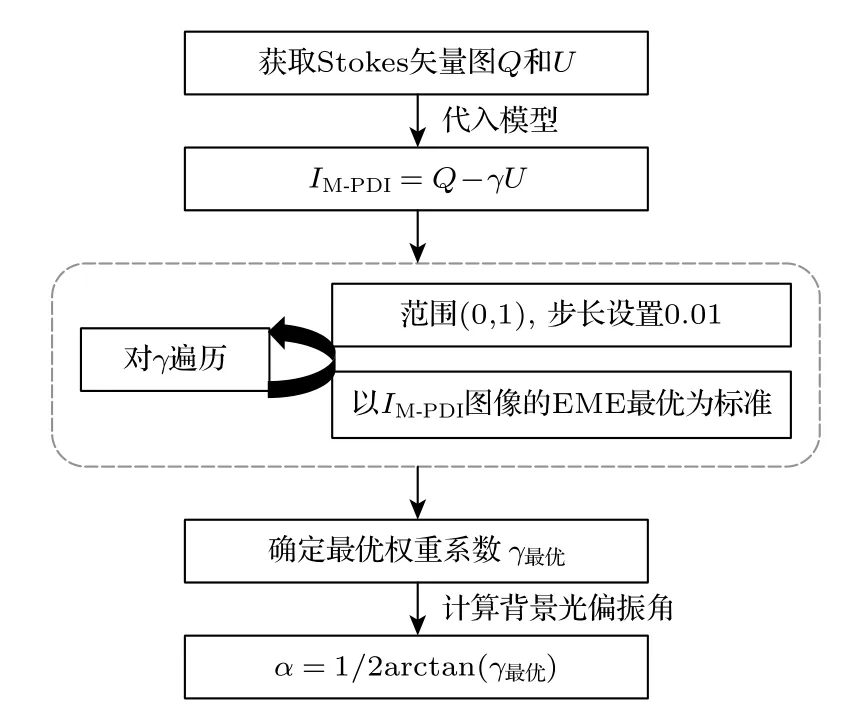
图2 基于M-PDI的背景光偏振方向研究方法流程图Fig.2.Flow chart of research method for polarization direction of background light based on M-PDI.

2.3 实验平台搭建与图像采集

实验布局及装置如图3所示,包括LED光源、线偏振片、玻璃水箱、成像目标和偏振相机.LED光源型号为恒洋光学GI-060403,功率为3 W,波长532 nm;线偏振片为恒洋光学GSP-25,通光孔径为25.4 mm,消光比为1∶1000,设计波长为400—700 nm;水槽大小45 cm×45 cm×12 cm.目标物为金属硬币,相机为Lucid偏振相机,采用Sony IMX250 MZR CMOS (Mono)传感器,分辨率2448 pixels × 2048 pixels,帧率22 fps,可同时拍摄4个不同的定向偏振图像(0°,45°,90°,135°),配置镜头参数为35 cm定焦.

根据《水质-浊度测定》(GB13200-1991)和《海水-浑浊度的测定-目视比色法》(F-HZ-DZ-HS-0053),目前一般采用福尔马肼、硅藻土或高岭土来配置浊度溶液.高岭土化学式为Al2O3·2SiO2·2H2O,具有优良的光散射能力,成分与天然浑浊水体具有相似性[22].一个浊度(NTU)的定义为1 L水中含有1 mg杂质,使用高岭土配置散射介质时,1mg/L 高岭土悬浊液呈现浊度为1 NTU.因此本研究使用高岭土调配不同浊度的水体环境,且本实验中仅将高岭土颗粒视为杂质.在水槽中注入10 L清水,使用电子天平按照每2 NTU为梯度进行浊度液体配置,水槽3个侧面和底面皆有黑色覆盖物以避免环境光的干扰和水箱壁的反射.在光源后放置线偏振片作为起偏器获取线偏振光源射入注水水槽中,将目标物置于水槽之中.目标物距与探测器间距离为35 cm,其中置于水中的距离为15 cm,置于空气中的距离为20 cm.光源与目标物间距离为35 cm,其中置于水中的距离为15 cm,置于空气中的距离为20 cm.入射光路和出射光路之间夹角为40°,探测角度应避免接收目标物的镜面反射光.目标物反射光通过浑浊水体后被偏振相机接收,在电脑端输出探测结果.

3 实验结果与讨论

3.1 M-PDI方法结果

在实验室搭建的探测环境中获取Stokes矢量图Q和U.通过改变水体浊度这一变量,开展普通光学探测方法和M-PDI的对比实验,实验结果如图4所示,图4(a)—(d)为普通光学探测方法的结果,图4(e)—(h)为M-PDI的结果.随着水体环境浊度的升高,两种方法中的目标信息光都随着散射光的增强而逐渐隐匿,但M-PDI结果目标的轮廓、细节信息和图像对比度明显始终优于普通光学探测方法结果.尤其是在高散射条件下,普通成像方式几乎无法分辨出目标物信息时,M-PDI的结果在高浊度条件下仍能区分目标物轮廓和大量的表面细节信息.这表明M-PDI可以除去部分散射光对水下成像的影响,改善图像质量.

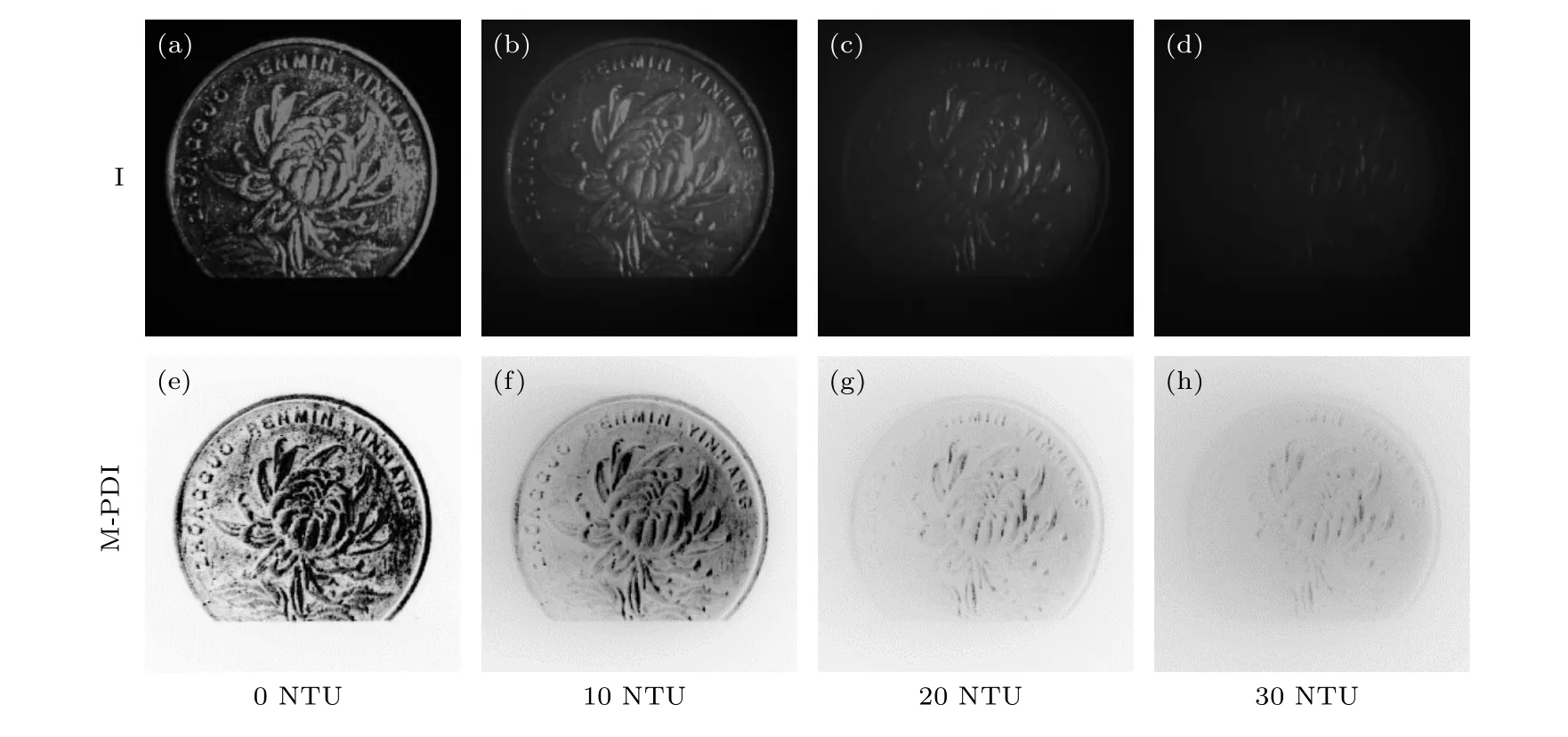
图4 0,10,20,30 NTU条件下传统探测结果和M-PDI探测结果对比Fig.4.Comparison between traditional detection results and M-PDI detection results under the conditions of 0,10,20 and 30 NTU.

为了更加直观精准地判断两种方法结果的差异,本文计算了两组结果的EME值开展定量分析,结果如表1所列.

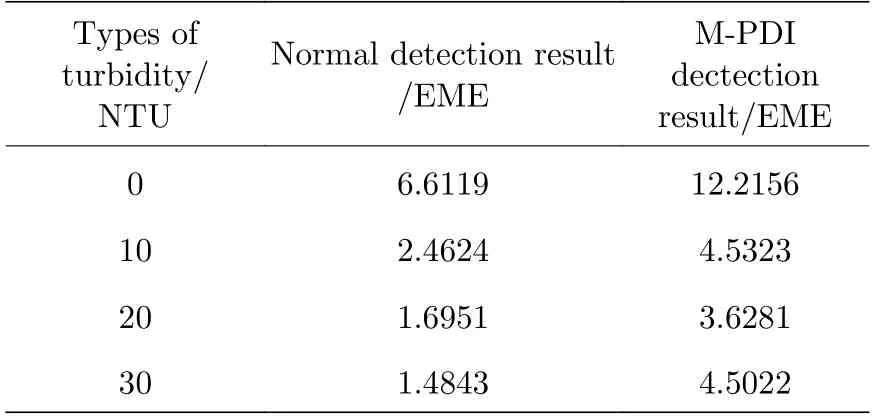
表1 传统探测结果和M-PDI探测结果EME值对比Table 1.Comparison of EME values between traditional detection results and M-PDI detection results.

表中数据结果说明,M-PDI结果的EME值始终显著优于普通光学探测方法结果.在表中所示的4种浊度条件下,M-PDI结果的EME值分别是普通光学探测方法结果的1.85倍、1.84倍、2.14倍、3.03倍.通过上述对比分析说明,M-PDI可有效抑制水下成像过程中散射光带来的影响,且在浑浊水体中更具有适应性,有效提升水下目标的探测能力.

3.2 M-PDI输出结果EME值与γ的关系

实质上,权重系数γ反映的是Stokes矢量中Q和U之间的耦合情况,其取值范围为(0,1).图5显示了浊度为20 NTU时M-PDI结果的EME值随γ变化的曲线.由图5可知,当γ为0.71时为最优权重系数,成像结果具有最大的清晰度,EME值为3.6281,这表明Stokes矢量中Q和U之间此时具有最佳的耦合效果.

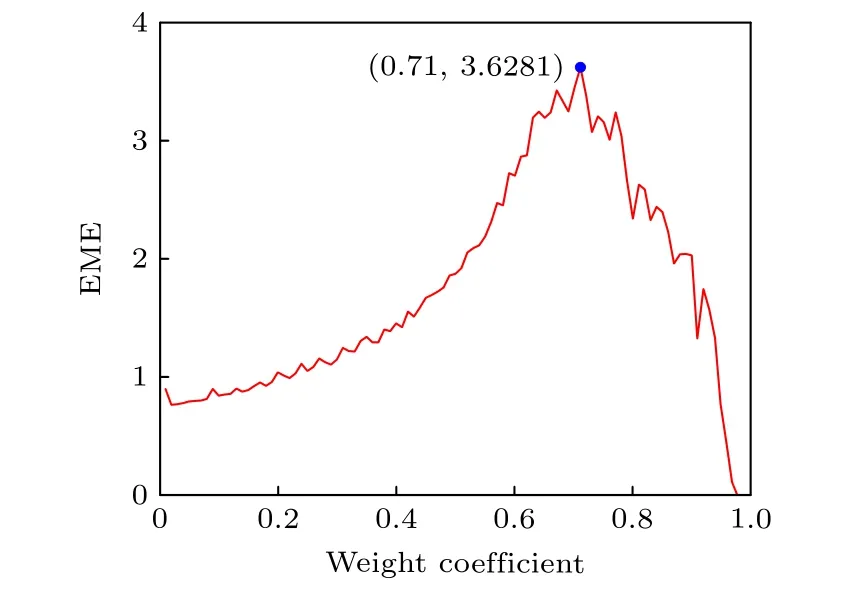
图5 20 NTU水体中M-PDI输出结果EME值与权重系数γ的关系Fig.5.Relationship between EME value and weight coefficient γ of M-PDI output results in 20 NTU.

3.3 γ随水体浊度变化的规律

本研究进一步探究了不同浊度水体条件下γ和EME值的变化情况.为确定参数的变化趋势,设置浊度梯度为2 NTU,分别对0—38 NTU的浊度范围进行偏振探测,并对获取的实验结果进行了分析,如图6所示.设置38 NTU为截止是考虑整个探测过程为恒定曝光,在34 NTU条件下视场中已经看不到目标物信息,再顺延2组数据以做过渡.

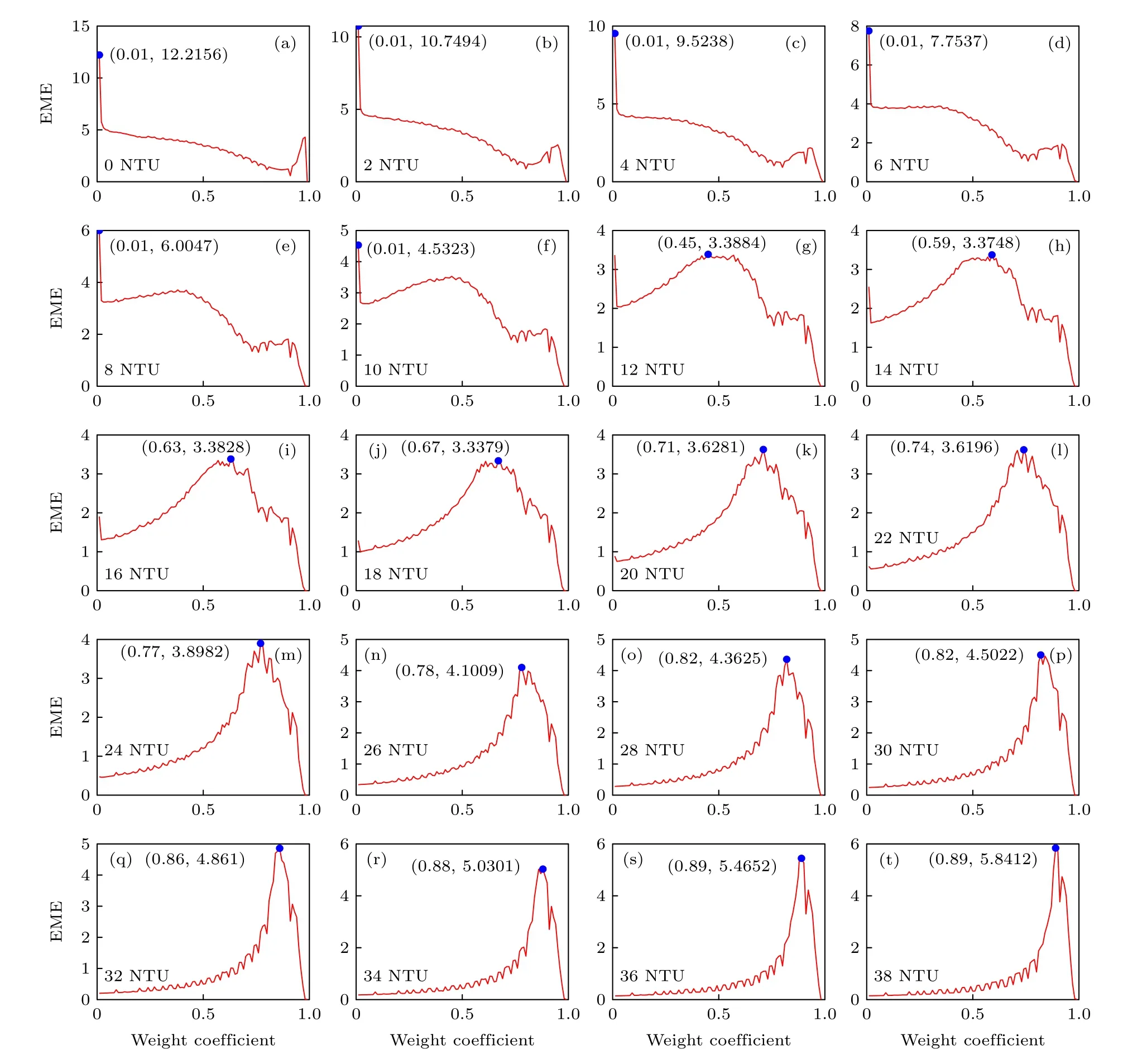
图6 0—38 NTU范围内γ和EME值的变化情况Fig.6.Changes of γ and EME values in the range of 0-38 NTU.

图6每个子图中的曲线峰值点,对应的横坐标值即为最优权重系数.在浊度较低的条件下(0—10 NTU),最优权重系数保持在0.01不变.在10—12 NTU条件下,最优权重系数发生突变,由0.01变化至0.45,此后最优权重系数随着浊度的升高而逐渐增大,如图7所示.

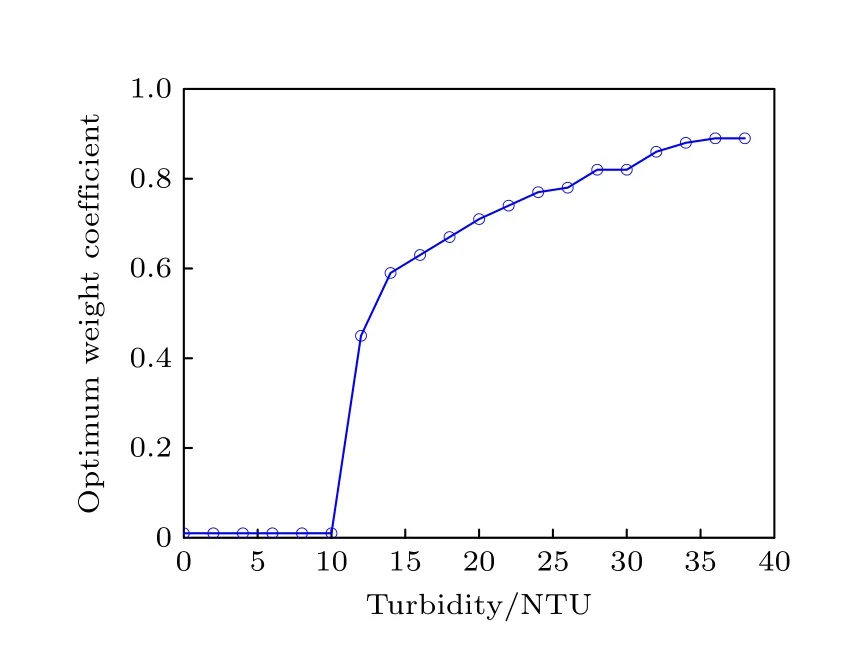
图7 最优权重系数在不同浊度下的变化趋势Fig.7.Variation trend of optimal weight coefficient under different turbidity.

当背景散射光的偏振方向α与正交偏振器件的方向各成45°时,背景散射光便可以被完全抑制,但这是较为理想的情况.在实际的探测过程中,由于前向散射和后向散射的偏振差异、以及所用仪器自身限制等原因,探测结果中背景散射光难以做到完全的抑制.尤其当水体的浊度增大时,水体环境带来的散射强度将远超过差分成像方式本身对散射光的抑制能力.由图7数据的变化趋势可知,在低浊度范围条件下,此时背景散射光的强度尚在M-PDI的抑制极限范围内,因此在0—10 NTU条件下的结果中,最优权重系数保持不变,表征为0.01.但随着水体浊度的增大,背景散射光的强度超越了M-PDI本身的抑制极限,背景散射光的影响显化,因此最优权重系数由0.01突变为0.45,此后在中高浊度条件下,EME与γ的相关曲线呈现出新的分布趋势.

图6数据表明EME值随浊度的增大逐渐降低,达最低点后出现小幅上升现象,如图8所示.探测器能够获取目标物信息代表目标物反射光成功传播到探测器接收面,因此基于偏振的探测方法代表接收端收到的光学信息是具备偏振特性的.不同的探测距离,接收面将接收到不同种类的光子.理想的条件是近距离探测,此时接收面可以接收到各种散射光子,例如非散射光子、单次散射光子、少量多次散射光子.随着介质长度的增大,探测器和目标物之间的光学长度增大,多次散射事件的数量增多,光线发生退偏振现象,这对应了水体浊度增大,结果的EME值整体呈现下降趋势并降到一个最低点的现象.在高浊度条件下实质上是等效了更远的探测距离,此时光子经历多次散射,大部分已经无法传播到接收端,此时接收端能够接收到的目标物信息大部分是少量的沿直线传播的弹道光子,其依旧保留着原始的偏振特性,因此输出结果在此条件下会出现EME值的小幅度回升现象.

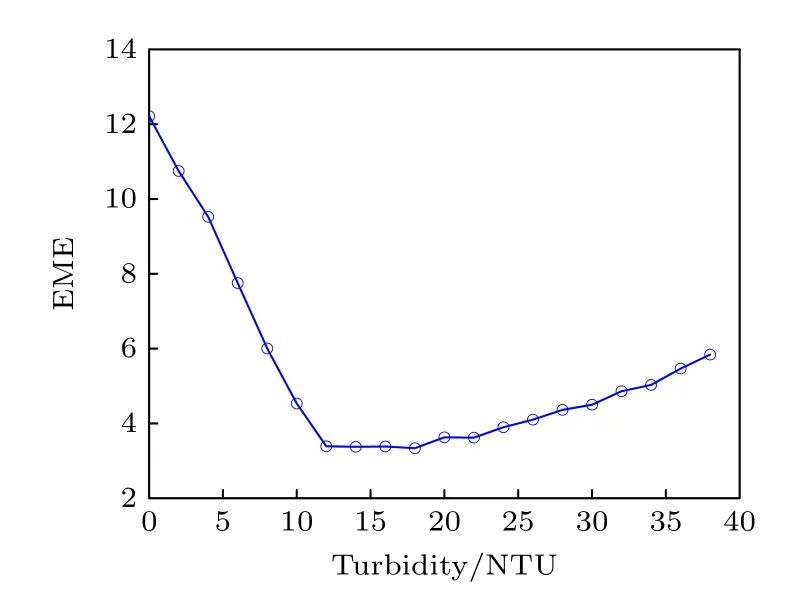
图8 EME在不同浊度下的变化趋势Fig.8.Trend of EME under different turbidity.

3.4 背景光偏振方向的变化规律

在获取不同浊度条件下的最优权重系数后,算出对应的背景光偏振方向α,获得表2所列数据.

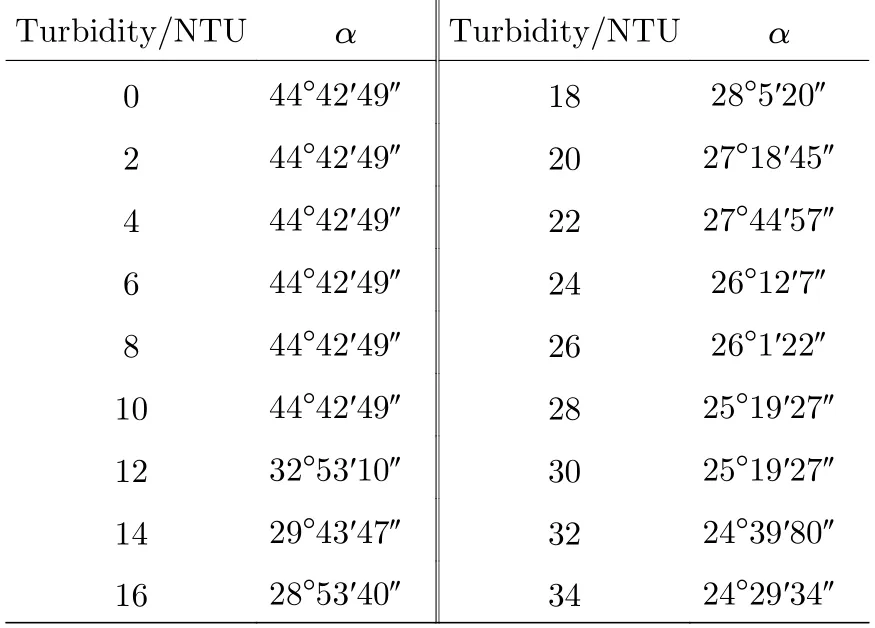
表2 不同浊度条件背景光偏振方向变化数据Table 2.Data on the variation of background light polarization direction under different turbidity conditions.

在低浊度条件下,基于最优权重系数计算出背景光偏振方向约为45°,该角度契合偏振差分方法中背景散射光与起偏器和检偏器间夹角互为45°实现共模抑制的理论关系.随着水体浊度的提升,该角度不断减小,逐渐趋于平行检偏器的方向,即呈现出与入射光偏振方向正交的趋势.值得强调的是,基于这种方法可以说明低浊度条件的背景光一直是被抑制的状态,基于本文构建的实验条件,抑制极限约为10 NTU.但是随着水体浊度的增大,背景光的影响逐渐显化,因此还需要结合其他手段才能对背景光进行进一步的抑制或者去除.此外,本文所提的抑制极限并非指0 NTU和10 NTU条件下可以得到相同清晰度的结果,而是指散射事件累计导致宏观偏振角度变化的极限.

为确保本研究结果的适应性,研究过程中开展了多次重复实验,包括更改目标物与光源、探测器在水中和空气中的距离,此处不再赘列数据.实验结果表明,空气介质中的距离改变对偏振信息几乎没有影响;水体介质中的距离改变时,若光经历的平均散射次数[23]近似,则背景光的偏振信息基本一致,因此γ和EME值的整体分布趋势不变,背景散射光的偏振方向变化趋势也不变;光源和目标物间的距离改变,只会影响目标物表面接收的光辐射强度,不会影响实验结果的整体变化趋势.

4 结论

本文基于Stokes矢量差分法分析了最优权重系数和M-PDI结果的EME值的耦合关系,提出了利用最优权重系数确定背景光偏振方向的研究方法.结合实验分析了M-PDI方法和普通水下光学成像方法的差异;研究了不同浊度水体中最优权重系数与M-PDI方法结果图像的EME分布趋势,基于最优权重系数计算背景光偏振角度;探究了M-PDI方法对背景散射光的抑制极限;最后分析了背景散射光偏振方向随水体浊度变化的趋势.研究结果表明,M-PDI方法可有效抑制水下成像过程中散射光带来的影响且在浑浊水体中更具有适应性;在低浊度范围和高浊度范围条件下,权重系数和M-PDI结果的EME值存在不同的分布趋势;M-PDI方法在低浊度条件时对背景散射光有很好的抑制效果,浊度升高后散射作用会重新显化并逐渐增强;背景散射光的偏振方向随水体浊度的上升呈现与入射光偏振方向正交的趋势.

本研究为确定水下成像背景散射光的偏振方向提供了方法依据.确定的背景散射光偏振信息可为水下光学成像的去散射工作提供思路.例如,可以根据背景散射光的偏振方向在高浊度水体中的角度特征,在工程硬件方面设计合理的偏振接收角度,在探测端避免或减小散射光的影响.还可以将M-PDI方法的结果与其他去散射算法结合,如暗通道去雾算法(UDCP)、水下偏振复原算法(CUV)或改进的偏振去雾算法(IDP)等,进一步提升水下光学图像的信噪比,从而提高水下目标的探测和识别效率.