高分子塌缩相变和临界吸附相变的计算机模拟和机器学习

罗启睿 沈一凡 罗孟波†

1) (杭州链坊科技有限公司,杭州 310013)

2) (浙江大学物理学院,杭州 310027)

1 引言

机器学习是一种人工智能技术,其基本思想是通过建立多层神经网络模型来实现对数据的学习和识别[1,2].机器学习使用大量的数据进行训练,可以自动从数据中提取出最优的特征表示,并在多个层次上逐步抽象数据的特征,从而实现高效的模式识别和分类任务.机器学习已成为图像识别、语音识别、自然语言处理、材料信息等领域的重要技术,并在多个领域得到广泛应用[3-6].近年来,机器学习也开始应用于材料研究和性能预测、高分子相变和玻璃态转变的研究中[7-9].

高分子相变是指高分子材料在不同温度及不同条件下发生的相变现象,包括熔融、结晶、凝胶化等过程,也包括高分子在溶液中的塌缩相变和在平面上的临界吸附相变.这些相变现象与高分子材料的物理性质密切相关,对高分子材料的制备和应用具有重要作用.塌缩相变是高分子稀溶液中一个重要的现象,随温度的变化高分子发生从伸展无规线团态到塌缩液滴态的转变,从而引发相分离.塌缩相变在纳米材料制备、药物传递等很多领域有广泛的应用[10].此外,高分子链在表界面的吸附是高分子科学和生物物理的重点研究领域之一.高分子在表面的吸附可以改变表面的性质,在制备高分子复合材料、改善材料表面性能、制备生物医用材料,以及印刷电路等许多技术和生物应用中有重要作用[11-13].因此,聚合物的塌缩和吸附相变得到了实验、理论和模拟的广泛研究[14-17].其中,研究塌缩相变温度和临界吸附温度是高分子科学研究中的重要的基础问题.

本文用朗之万动力学方法产生了稀溶液中不同温度的高分子构象,利用均方回转半径随温度的变化确定了高分子塌缩相变的温度,机器学习则通过计算伸展无规线团态和塌缩液滴态的概率得到高分子塌缩相变的温度.本文也用动力学Monte Carlo方法模拟了低接枝密度的接枝高分子的临界吸附现象,利用吸附链节数的涨落确定了高分子临界吸附温度,同时获得了不同温度的大量高分子构象,然后机器学习通过计算高分子处于脱附态和吸附态的概率得到高分子临界吸附相变的温度.研究发现模拟和机器学习得到的高分子塌缩相变温度和临界吸附相变温度几乎相同.动力学Monte Carlo和郎之万动力学是研究高分子热力学性质的两个重要的模拟方法,本文分别用这两种模拟方法模拟了高分子的塌缩和临界吸附相变,并分别与机器学习进行了比较.

2 模型和研究方法

利用计算机模拟和机器学习的方法研究稀溶液中高分子的塌缩相变温度和低接枝密度的接枝高分子的临界吸附温度.对于稀溶液中高分子的塌缩相变,用朗之万动力学方法模拟了高分子均方回转半径随温度的变化,估算了塌缩相变温度;对于接枝高分子在吸引平面上的临界吸附,采用动力学Monte Carlo方法模拟了吸附链节数随温度的变化,估算了临界吸附温度.然后利用大量不同状态的高分子构象数据对神经网络进行训练,完成训练后的神经网络从不同温度的高分子构象中计算出高分子处于塌缩液滴态及吸附态的概率.最后,利用从机器学习得到的高分子状态概率变化的极大值估算高分子塌缩相变温度和临界吸附温度,并与模拟结果进行了比较.

2.1 模 型

采用粗粒化的珠簧高分子模拟,链长为N的高分子链由直径为σ的链节组成.为简化模拟系统并加快模拟速度,将溶剂看成背景.溶剂分子与高分子的随机相互作用提供模拟系统的随机力,而高分子运动带动溶剂分子的运动则表现为高分子链受到溶剂的黏滞力.图1给出了两个模拟系统的高分子示意图: 稀溶液中高分子和低接枝密度的孤立接枝高分子.在这两个系统中,高分子链之间相互作用可以忽略,因此模拟系统内只考虑一条高分子链.高分子链内的相互作用包括成键链节之间的相互作用和非成键链节之间的相互作用,接枝高分子链还存在链节与平面的相互作用.

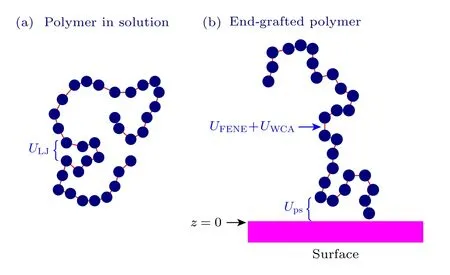
图1 模拟高分子的示意图 (a) 稀溶液中的高分子;(b) 低接枝密度的孤立接枝高分子Fig.1.Schematic diagram of simulated polymers: (a) A polymer in dilute solution;(b) an isolated grafted polymer at low grafting density.

成键链节之间的相互作用包含有限伸展的非线性弹性(finitely extensible nonlinear elastic,FENE)势:

以及链节-链节之间成对的纯排斥Weeks-Chandler-Andersen (WCA)势[20]:

这里b是键长,K=30ε/σ2是键的弹性系数,R0=1.5σ是最大键长,ε是WCA势的相互作用强度.FENE势和WCA势的共同作用决定了键的平均长度约为1σ.高分子中非键连的链节之间的相互作用采用截断的Lennard-Jones (LJ)势:

其中r是链节之间的空间距离.为了加快计算速度,LJ相互作用的计算在rcut处截断.如果取rcut=21/6σ,LJ势演变为WCA势,链节之间只考虑短程的排斥作用.如果取rcut＞ 21/6σ,模拟还考虑链节之间的相互吸引作用.在塌缩相变的研究中,取rcut=2.5σ,链节之间的吸引作用在低温下引起链的塌缩;而在临界吸附的研究中,取rcut=21/6σ,高分子链节之间为纯排斥作用,高分子总是处于伸展无规线团状态.

在临界吸附的研究中,高分子的一端接枝在平面上.平面位于z=0,接枝链节中心位于z=1的位置.假定一个厚的无限大平面,高分子链节与平面的相互作用势取[21]:

这里z是链节离开平面的垂直距离,εps是平面的吸引强度,取截断距离zc=4σ 和

当zmin=0.8585σ,Ups取极小值 -εps.当链节位于zmin＜z＜ 1.22σ 时,势能值小于-0.5εps,认为这样的链节为吸附链节.模拟中平面的吸引强度εps固定为ε.

模拟中的物理量均是约化的无量纲量,取长度单位σ=1,能量单位ε=1,和链节的质量为质量单位m=1.温度的单位为 ε/kB,其中kB是玻尔兹曼常数.

2.2 朗之万动力学方法

高分子链节的运动方程采用朗之万(Langevin)方程:

其中 -∇U代表相互作用力,F(T)是热运动随机力,-ηvi是黏滞力.F(T)具有高斯分布,其平均值为0,涨落为6ηkBT.链节的位置和速度的演化过程采用修正 velocity-Verlet 算法.

模拟的时间单位为τ0=(mσ2/ε)1/2.模拟中黏滞系数取η=1,模拟的时间步长取δt=0.01τ0,每间隔δt时间高分子链节的位置和速度同步演化一次.

采用模拟退火的方法得到高分子不同温度的构象.从高温的初始无序态高分子构象出发,缓慢地降低模拟温度,前一个温度的高分子构象作为后一个温度的高分子初始构象.在每个温度,长时间模拟得到平衡态,然后用更长的模拟时间统计高分子链的模拟数据.由于温度的改变非常小,高分子构象的平衡通常都比较快.为了选择正确的模拟时间,会先对少量样本做一个预模拟,观察与高分子构象相关的物理量的收敛过程,估算出平衡时间和弛豫时间.

2.3 动力学Monte Carlo方法

在动力学Monte Carlo方法中,高分子链的整体运动通过高分子链节的局域移动来实现.高分子链节的局域运动导致高分子链构象的变化,这种构象变化可以通过构造一个Markov过程来实现,即假定高分子链原来处于构象{r},通过链节运动以一定的转移概率P({r}→{r′}) 得到新的构象{r′}.链节局域运动成功与否采用Metropolis算法决定,即该转移概率P取P=min[1,exp(-ΔE/kBT)],其中ΔE是构象转变前后的能量差,即ΔE=E{r′}-E{r}.

链节的每次局域运动对应于链节在x,y和z方向分别移动dx,dy和dz,其中dx,dy和dz是介于(-Δ,Δ)之间均匀分布的随机量,模拟中取Δ=0.1σ.Monte Carlo的时间单位为Monte Carlo步(MCS),1个MCS中每个高分子链节平均运动一次.与朗之万动力学模拟相同,动力学Monte Carlo方法也采用退火模拟的方法得到高分子构象随温度的变化.

2.4 机器学习

采用机器学习中的监督学习模式,建立了基于神经网络的分类器.高分子链的空间构象通过链节序列的数据来表示,每个数据点代表每个链节所处的空间位置.在塌缩相变的研究中,链节序列的数据反映了高分子链处于伸展无规线团态或塌缩液滴态;而在临界吸附相变的研究中,链节序列的数据反映了高分子链属于吸附或者非吸附两种状态的一种.机器学习的任务是: 神经网络分析输入的高分子构象的链节序列数据,正确输出该高分子构象所属的状态概率.经典的机器学习方法有循环神经网络(recurrent neural network,RNN)及长短期记忆(long-short term memory,LSTM)等神经网络结构[22].但是对于高分子链来说,循环神经网络可能存在一定问题.循环神经网络会认为后时刻输入的内容与前面时刻输入的内容完全无关,因此后输入的链节数据可能会赋予极高的判断权重,而早期的链节数据会被“遗忘”,这与所有链节等效的物理事实不符.而长短期记忆神经网络可以克服这个问题.与一般的前馈神经网络不同,长短期记忆神经网络可以利用前后数据的时间序列对输入进行分析,在自然语言处理方面有广泛的应用[22].

考虑到高分子链节的顺序排列性,长短期记忆神经网络可以有效地处理高分子构象的长数据特征,从而正确得到高分子链节数据与高分子链构象类型的映射关系.因此,本文处理高分子链的构象数据的核心神经网络的是长短期记忆网络.图2给出了机器学习进行数据处理的流程图.

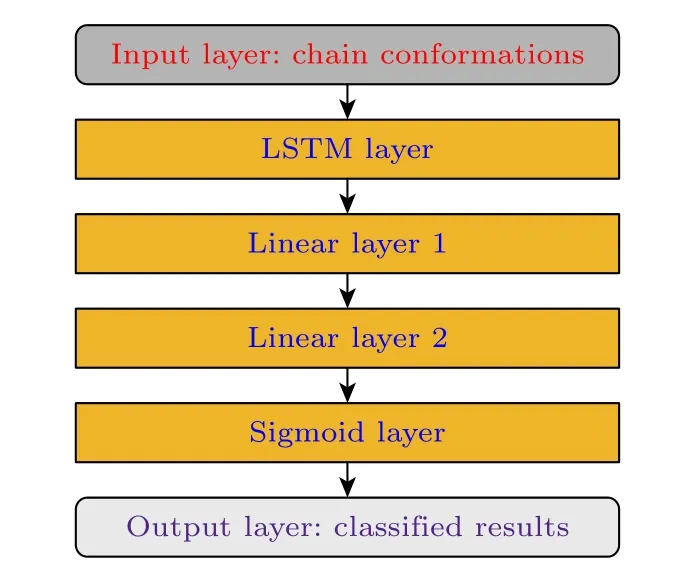
图2 机器学习的流程图Fig.2.Flowchart of machine learning.

长短期记忆神经网络的LSTM层接收高分子链各个链节的空间坐标信息,并和当前的LSTM层状态进行计算,输出新的状态.完成高分子链构象所有链节数据的计算后,LSTM层最后输出的状态向量是该高分子链构象在高维嵌入空间中的一个表达.接下来的两个线性层都做数据的空间降维工作.第一个线性层负责将数据从高维嵌入空间变换到一个较低维的隐藏空间,第二个线性层再将隐藏空间变换到最后的标签空间.激活层用sigmoid函数将数据转换成(0,1) 之间的数,然后输出层输出该值表示该高分子构象中处于所属状态的概率.

监督学习需要有一个训练过程,因此先对神经网络进行训练和验证.收集高温和低温的高分子构象,假设在这两种温度下,几乎只会生成对应两种状态的高分子链构象,取其中75%的数据作为训练集,剩余25%的数据作为验证集.我们设置验证的成功概率大于0.9999以保证我们的学习效果.本文的神经网络模型使用二分类交叉熵损失(binary cross entropy loss)作为损失函数,使用AdamW优化器[23].在训练时,二分类交叉熵损失结果意味着神经网络输出结果和期望结果的差异,重复训练过程直到损失收敛.图3给出了损失随训练次数的变化.由图3可以看到,损失随训练次数的增加先快速下降,然后快速收敛到一个稳定值.根据图3的结果,在训练次数达到40的时候,认为该机器学习模型已经收敛.因此在实际训练中,设置训练次数为40,在确保模型效果的情况下节约计算时间.

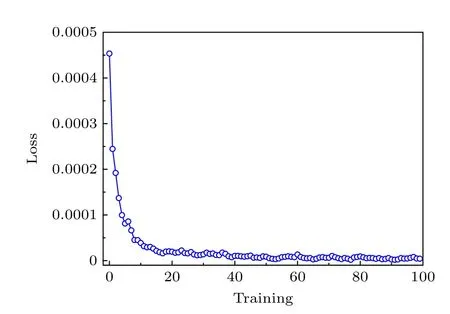
图3 机器学习中的损失随训练次数的变化Fig.3.Loss in machine learning varies with the number of trainings.

完成长短期记忆神经网络训练以后,把高温和低温之间的其他温度的高分子链构象作为测试集,判断各个温度下的高分子构象处于给定状态的概率.最后对同一温度的所有高分子构象的状态概率求平均,得到该温度下高分子处于某一状态的概率的统计平均值.

本文的神经网络模型中LSTM层使用双向LSTM结构,内部为三层双向LSTM,每层单方向有200个隐藏神经元,共有1200个神经元.第一线性层有400个隐藏神经元,第二线性层有80个隐藏神经元,最后的激活层有一个sigmoid神经元.因此处理1个数据的神经元数目为1681.输入层使用1000的批大小,即一次同时输入和处理1000条高分子构象数据.这样,神经网络模型中总神经元数量达到1681000.机器学习使用Python语言,基于PyTorch 框架搭建了机器学习程序,在支持CUDA 的 Nvidia GPU上运行.为了能处理不同长度的高分子链的数据,把每条数据长度固定为80,长度不足的数据会自动用0补齐.对不同链长的高分子构象均得到相同的结论,因此本文给出的数据是模拟中所用的最大链长的计算结果.

3 高分子的塌缩相变

在塌缩相变的研究中,还考虑了高分子链节之间的短程屏蔽库仑势[24],即把高分子链视作聚电解质.引入静电相互作用大幅降低了塌缩相变温度,也同时降低了模拟的温度区间,减小了热运动的无序涨落,从而可以使用较大的模拟时间步长,加快模拟的速度.用朗之万动力学方法模拟了链长N=64的高分子构象性质随温度的变化,图4给出了高分子的均方回转半径对温度的依赖关系.模拟在一个考虑周期性边界条件的三维立方系统中进行,系统的尺寸L取约为最高模拟温度(T=3.2)高分子的方均根回转半径的10倍,即L≈.每个高分子构象的平方回转半径定义为高分子链节距离质心的平均平方距离,即

其中rj是链节的位矢;rc是高分子质心的位矢.是76000个独立高分子构象的平均.高分子的随着温度的降低而减小,表明高分子构象发生了从高温的伸展无规线团(coil state,C态)态到低温的紧缩液滴(globule state,G 态)态的转变,即塌缩相变.塌缩相变温度Tc通常定义为随温度变化最快时对应的温度,即极值处.从图4的插图,得到Tc=0.5,这与之前的模拟结果接近[24].

比较了不同温度下高分子构象的差别,图5给出了3个特殊温度下(极低温、塌缩相变温度和极高温)高分子的归一化概率分布.在极低温T=0.01,从图5(a)的分布可以看到不同构象的差别极小,分布在2.5到3之间很小的区间范围内.如图5(a)插图所示,高分子的构象是一个紧缩的液滴状.而在远高于塌缩相变温度的高温,如图5(c)的温度T=3.2,高分子的变化范围很宽,主要变化范围为从10到60,远大于紧缩液滴状的.这表明,虽然高分子的构象很多,但基本上都处于伸展的无规线团状,如图5(c)的插图.在塌缩相变温度Tc=0.5,如图5(b)所示,高分子的变化范围从4到30,涵盖了近紧缩液滴状构象和伸展无规线团状构象.我们看到随着温度的变化,高分子构象的分布也随之发生变化,这正是机器学习的基础.

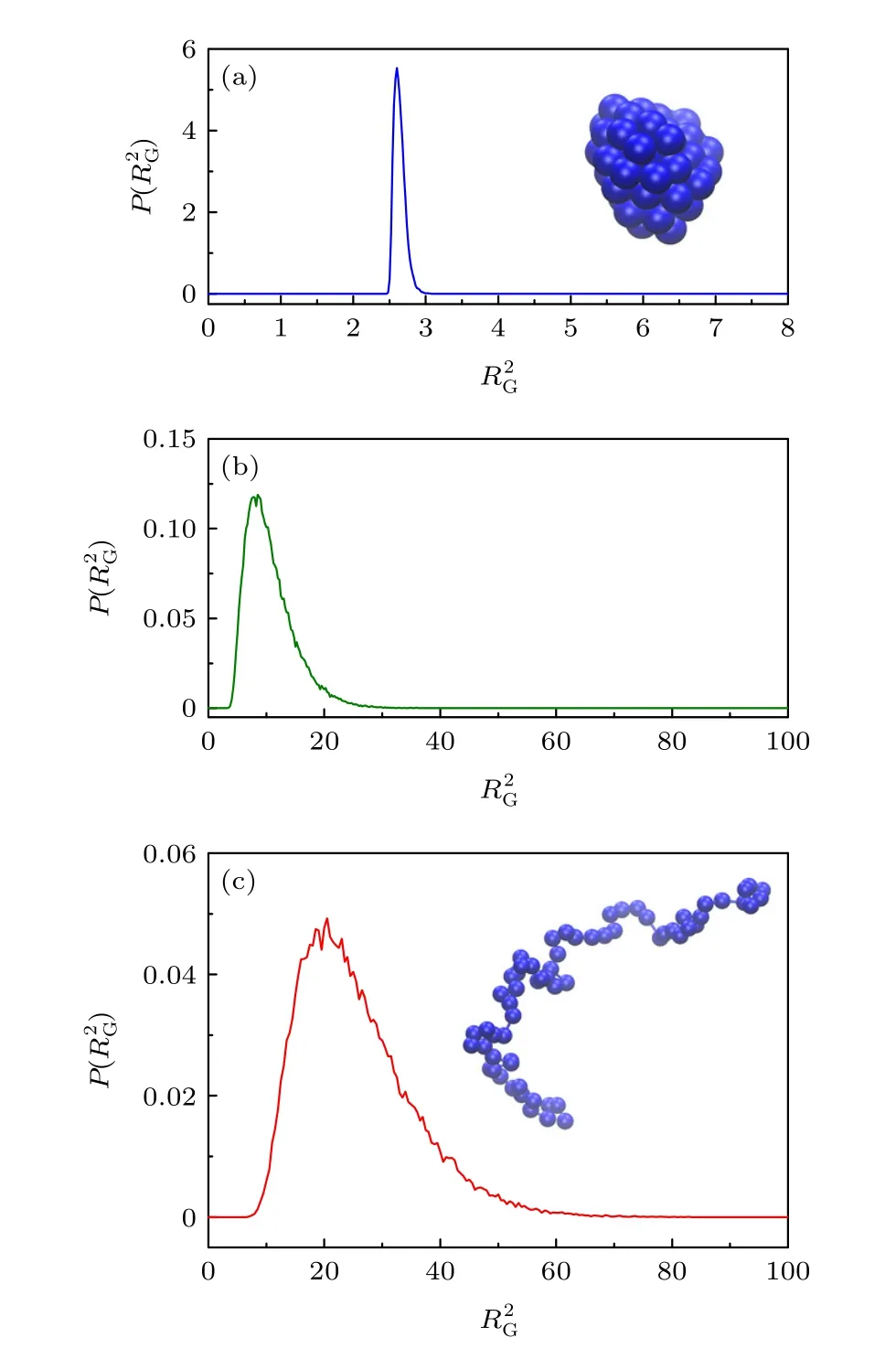
图5 高分子平方回转半径 在温度T=0.01 (a),0.5(b)和3.2 (c)的概率分布.插图分别给出了T=0.01和3.2时高分子的典型构象Fig.5.Plots of the probability distribution of square radius of gyration for polymer at temperatures T=0.01 (a),0.5 (b),and 3.2 (c).The insets show the typical polymer conformations at T=0.01 and 3.2.

然后用基于长短期记忆神经网络的机器学习方法计算了高分子链处于塌缩态的平均概率PG.每个温度下高分子的构象数目均为76000.在机器学习的训练阶段,假定高分子在模拟的最低温(T=0.01)均处在G态而在模拟的最高温(T=3.2)都处于C态.这种假定的合理性通过成功率大于0.9999的构象验证得到保证.对长短期记忆神经网络训练以后,机器学习自动计算不同温度的高分子处于塌缩态的概率.高分子链处于塌缩态的平均概率PG随温度的变化结果见图6.由图6可以看到,PG随温度的升高而下降,表明高分子的构象发生了从G态到C态的转变,在T=0.5附近构象的转变迅速增加.图6的插图给出了概率随温度的变化率|dPG/dT|,|dPG/dT|的峰值位置在T=0.5,表明在T=0.5高分子的状态变化最快,即机器学习得到的塌缩相变温度为0.5,与模拟结果一致.这表明机器学习通过学习C态和G态的高分子构象,能有效地判断其他高分子的构象特征,从而给出符合模拟结果的塌缩相变温度.

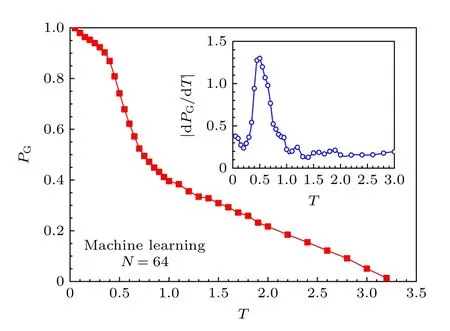
图6 高分子处于塌缩态的平均概率PG与温度T关系的机器学习结果.插图给出了|dPG/dT| 随T的变化.Fig.6.Machine learning results of the mean probability of polymer being in the compact globule state,PG,versus temperature T.The inset shows the change of |dPG/dT| with temperature T.

这里需要指出模拟结果只给出了高分子构象数据和构象性质的统计平均值,如图4所示,并不能给出高分子处于G态和C态的概率,而机器学习则从高分子构象判断出高分子的状态,如图6所示.虽然模拟和机器学习的一致性不能直接通过状态的概率来比较,但可以通过临界温度的数值的一致性来比较.

4 高分子的临界吸附相变

高分子的吸附伴随着吸附能量或者吸附链节数的变化,高温脱附态的吸附能量低而构象熵大,低温吸附态的吸附能量大而构象熵小.高分子吸附过程是一个能量和熵的变化和竞争过程,临界吸附点定义为能量和熵的竞争平衡点.吸附过程中平均吸附链节数〈M〉随着温度的下降而持续增大.高分子的临界吸附相变通常被认为是连续相变,在临界吸附相变温度,由于高分子不断的吸附和脱附,吸附链节数的涨落(类似于热容):

达到最大[15,25].模拟研究中常利用吸附链节数的涨落来标定高分子链的临界吸附温度[25].

用动力学Monte Carlo方法模拟了链长N=65的接枝高分子链的吸附.无穷大平面位于z=0,平面的边长L也取约为最高模拟温度(T=4)高分子的方均根回转半径的10倍,即系统的高度大于高分子完全伸直的长度.在平行平面的方向考虑周期性边界条件.高分子的第一个链节中心固定在平面中心位于z=1的位置,模拟中定义z＜ 1.22 的其他链节(除接枝链节)为吸附链节.图7给出了链长N=65的高分子吸附链节数的涨落与温度T的关系.模拟得到高分子的临界吸附温度约为Tads=0.9.注意到因为本工作中平面对高分子的吸引势((4)式)是文献[26]的0.95倍,我们的模拟结果与之前朗之万动力学的模拟结果相近[26].图7的插图显示了高温的非吸附态(non-adsorption state或desorption state,D态)和低温的吸附态(adsorption state,A态)两种典型的高分子构象: 高温时高分子呈现为蘑菇状的脱附态,低温时高分子呈现为吸附态.可见,高分子在吸附前后的构象也发生了明显的变化.

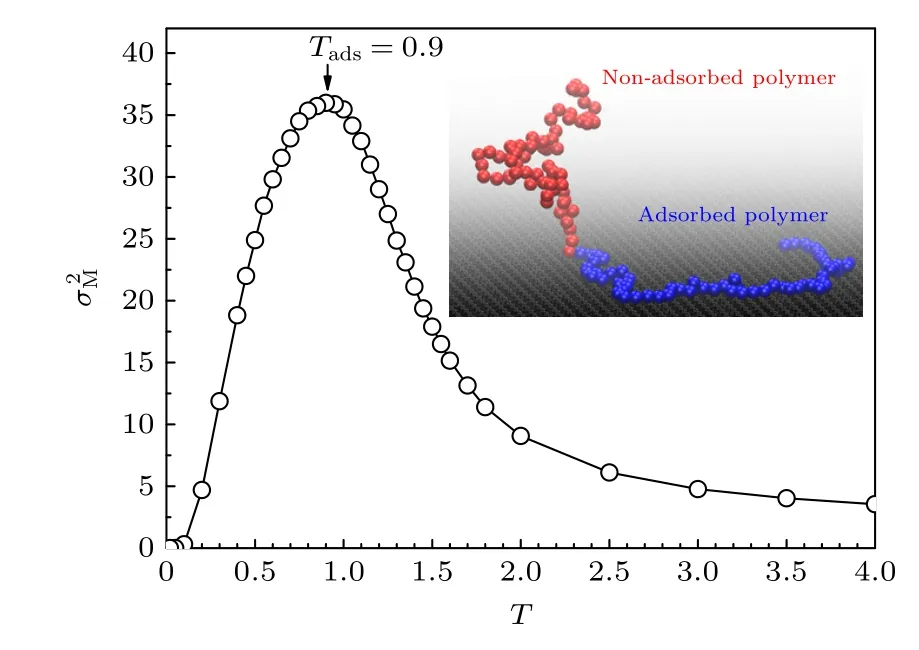
图7 高分子吸附链节数涨落 与温度T的关系的动力学Monte Carlo模拟结果.插图给出了高温的非吸附态和低温的吸附态高分子构象Fig.7.Plot of the fluctuation of adsorption monomer number of polymer chain versus temperature T.The inset presents non-adsorbed polymer at high temperature and adsorbed polymer at low temperature.

基于长短期记忆神经网络的机器学习通过学习脱附态和吸附态的高分子三维构象,然后自动给出了不同温度下高分子处于吸附态的平均概率PA,结果如图8所示.这里每个温度的高分子构象数为248640.机器学习的结果也显示高分子从低温的完全吸附态过渡到高温的完全脱附态,与模拟结果一致.从温度变化率|dPA/dT|随温度的变化可看到,高分子状态变化最激烈的温度在T=0.9附近,与模拟得到的临界吸附温度Tads=0.9一致.

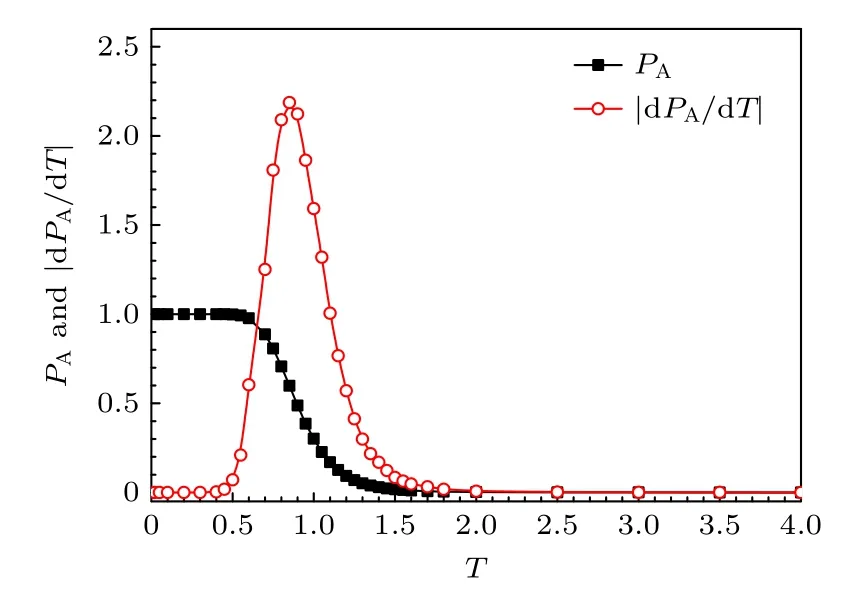
图8 高分子处于吸附态的平均概率PA和温度变化率|dPA/dT|与温度T的关系的机器学习结果Fig.8.Plot of the mean adsorption probability PA of polymer and its temperature change rate dPA/dT versus temperature T.

从图7的插图可以看到,吸附链与脱附链构象的最大区别体现为链节离开平面的距离(z坐标)的区别,即吸附链节数的区别,而描述高分子构象尺寸的平方回转半径的差别并不是很明显,因此我们认为机器学习主要通过区分高分子构象的链节z坐标来实现的.为此,只让机器学习分析高分子构象的链节z坐标,而忽略它们的x和y坐标.图9给出了分别利用高分子构象的三维坐标和z坐标进行机器学习得到的高分子处于吸附态的平均概率PA与温度T的关系.发现两种方法得到的差别比较小,说明机器学习在研究临界吸附时主要分析了构象的z坐标.但在临界吸附温度Tc附近,PA的值有一些差别,这说明在Tc附近,三维构象还是对机器学习有一定的影响.这可能是在Tc附近,高分子构象的变化非常大,这个时候z坐标不能唯一决定PA,高分子状态可能还跟链节的z的变化序列相关.

图9 利用高分子构象的三维坐标和z坐标进行机器学习得到的高分子处于吸附态的概率PA与温度T的关系Fig.9.Relationship between adsorption probability PA and temperature T obtained by machine learning using the three-dimensional coordinates and z-coordinates only of polymer conformations.

进一步分析了每个高分子构象的机器学习结果与构象性质之间的关联.关联了总共248640个构象的吸附数M和链质心高度zc与机器学习得到的每个构象可能处于吸附态的概率PA,找出PA在(0,0.2),(0.2,0.8)和(0.8,1)三个范围内高分子构象的分布.图10给出了临界吸附温度Tc=0.9 时的结果.发现小的PA对应于小的M和大的zc,而大的PA对应于大的M和小的zc.这说明机器学习的结果是符合物理预期的.在PA∈ (0.2,0.8)区域有一段重叠区,在这段重叠区内,虽然高分子的M和zc相同,但高分子构象变化范围大,因此具有各种不同的状态和PA值.这说明PA不是M和zc的单值函数,机器学习对高分子构象的判断还与构象的其他因素有关,这也与图9的结论相符.

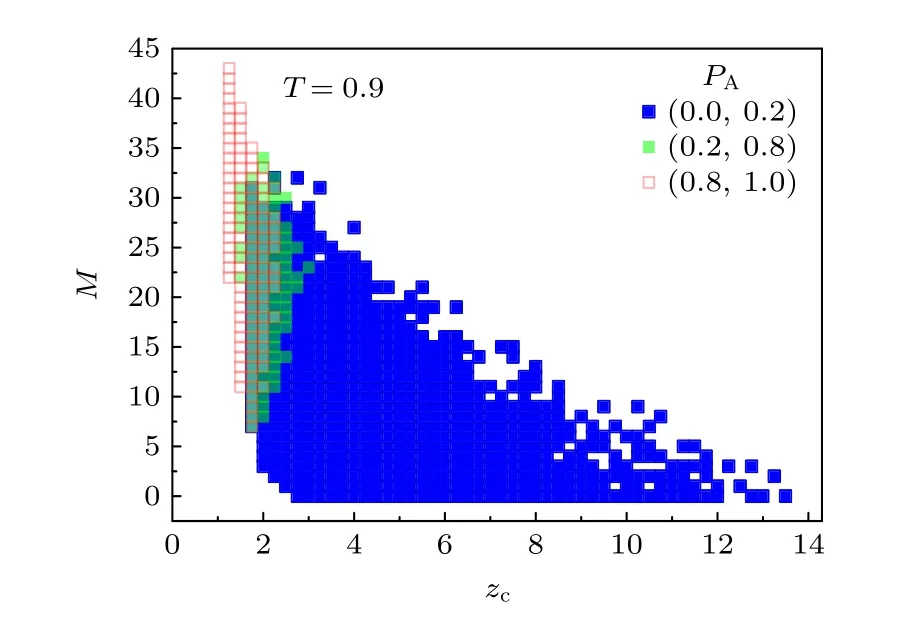
图10 机器学习得到的吸附态概率PA在(0,0.2),(0.2,0.8)和(0.8,1)三个范围内高分子构象相对于构象的吸附数M和链质心高度zc的分布Fig.10.Distribution of polymer conformation relative to the adsorbed number M and the mean height zc for the adsorption probability PA obtained by machine learning in three ranges of (0,0.2),(0.2,0.8) and (0.8,1).

5 结论

本文模拟研究了高分子的塌缩相变和临界吸附相变,得到了大量的高分子构象数据.机器学习采用长短期记忆网络作为核心神经网络,对高分子链构象按塌缩态和吸附态进行了分类统计.结果表明: 模拟和机器学习得到了相同的塌缩相变温度和临界吸附相变温度,机器学习的结果符合物理预期.本文的研究扩展了机器学习在高分子构象识别方面的应用,有望应用到高分子材料在不同温度下的相变行为的智能自动分析中.