计及多脉冲回击电流及电晕电流效应的输电线路耦合雷电过电压特性
2024-01-06桂重韩永霞刘刚
桂重,韩永霞,刘刚
(1. 中国能源建设集团广东省电力设计研究院有限公司,广州 510663;2. 华南理工大学电力学院,广州 510641;3. 南方电网科学研究院,广州 510663)
0 引言
有资料显示,由雷击引起的输电线路跳闸率占总跳闸事件的60%以上,雷电回击电流所形成的强磁场使得输电线路耦合形成瞬时、高峰值过电压波,从而引起设备绝缘击穿、线路跳闸等事件[1-4]。无论是传统电力还是新型电力系统雷击事件均会对其稳定运行构成严重威胁。
目前,很多学者采用不同维度时域有限差分(finite-difference time-domain,FDTD)[5-7]、解析解[8]等方法建模对雷击线路、杆塔以及临近区域空间电磁场变化情况进行求解,并结合不同过电压耦合模型研究其电压峰值变化趋势,证实了这些方法在线路耦合过电压研究工作中的正确性。同时,部分学者研究表明:当雷击事件发生时,在输电线路、绝缘子串周围所形成强电场超过临界阈值时,使得周围电场被击穿,形成电晕放电现象[9-12]。而电晕放电会在输电线路表面形成电离层,从而会抑制过电压峰值,即电晕效应能够启到过电压峰值屏蔽作用。其中,文献[13]指出电晕放电效应能够使同塔双回线路不同相线耐雷水平提升4%~9%。因此,为更加精确地研究输电线路耦合雷电过电压变化趋势,电晕放电效应是必不可少的重要因素之一。
同时,在研究雷电过电压工作中正确选取激励电流源对研究结果的准确与否启到关键作用,Heidler[14]早在1985 年就建立了回击电流峰值随时间变化的趋势模型,而后Rachidi[15]在Heidler 研究的基础上提出了更加精确的双Heidler 回击电流函数,同时该回击电流函数也是被学者广泛使用的激励电流源。但在现有的研究工作中均采用双Heidler回击电流函数触发一个回击电流脉冲,但早在2004年有观测实验表明,雷击事件以多脉冲回击电流形式占51.6%[16]。更有研究资料显示,在短短的毫秒为单位的时间内,一次回击过程包含了4 次电流峰值,且电流峰值逐渐降低[17]。国内部分学者更多的是结合冲击试验设备,站在试验的角度研究在多脉冲回击电流冲击下线路耦合过电压变化趋势[18-19]。因此,研究输电线路耦合雷电过电压变化趋势,多脉冲回击电流也是必不可少的另一个重要因素,但现有的研究均基于多脉冲发生器从试验角度进行研究,并没有建立相应的理论支撑依据。
基于上述分析,本文以双Heidler 回击电流为基础在考虑电晕放电效应抑制作用的情况下建立了触发3 个脉冲的回击电流模型,并采用“蛙跳格式”算法建立雷击电流空间电磁场计算模型,结合过电压耦合模型研究了多脉冲回击电流对输电线路耦合过电压的差异性。本文研究综合考虑了回击电流多个脉冲作用以及电晕电流屏蔽效应的影响,研究结论能够更加真实地反映出回击电流对线路耦合过电压的影响,能够为输电线路防雷路径优化提供科学的指导意义。
1 计算模型理论
1.1 激励电流源
激励电流源的准确选取对确保输电线路耦合过电压计算结果的有效性具有重要意义。文献[20]结合8/20 μs 雷电标准波形,对双Heidler 回击电流函数推导出多脉冲回击电流等效模型,能够较好地运用于多脉冲回击电流研究工作中。同时,文献[21-22]采用多脉冲回击电流对压敏电阻失效特性进行研究,更有文献[23]提到10个脉冲回击模型。
在本文的研究工作中,主要对触发3 个峰值脉冲电流进行过电压研究,因此计算多脉冲电流源模型可以改写为:
式中:I1、I2、I3分别3 次雷电流峰值;η为峰值修正因子;n为电流陡度因子;τ1、τ2为分别为雷电流上升、延迟时间。本文触发的3 个脉冲回击电流总时间控制在8 μs之内,满足一次闪击过程放电几十个微秒时间间隔,通过设置ω1、ω2、ω3振荡周期取值,使其每个峰值电流在8 μs内只振荡一次,这样即可实现触发3个脉冲峰值电流。
1.2 电晕放电效应
在雷击事件发生时,会使得输电线路小空间范围内电场强度增强,当达到临界阈值时,会发生空气间隙击穿放电现象,同时放电电荷会在输电线路近区迅速汇集,从而对雷电波的影响形成屏蔽作用。文献[24]结合多导体传输理论给出电晕放电效应作用下输电线路耦合过电压与回击电流的关系模型如式(2)所示。
式中:C(u)为考虑电晕效应的等效电容;L0为输电线路电导;u(x,t)、i(x,t)分别为雷电波在输电线路各个点位形成的耦合过电压、电流;Zt(t)为雷电流传播t时刻的接地阻抗;⊗为张量积。
但现有的研究均是立足于单个峰值回击电流推导出的电晕放电效应模型,而在本文的研究工作中考虑3个峰值电流,随着第2、3个回击电流的叠加作用,将使得输电线路表面电晕屏蔽效应越来越显著,导致单个脉冲推导出的电晕放电效应模型适用性较弱。因此,本文对式(2)进行改进,综合考虑3个峰值脉冲作用下电晕放电效应作用模型如式(3)所示。
式中ij(x,t)为第j个雷电流。
1.3 耦合过电压计算
目前,FDTD 算法采用网格化的思路,能够将TM 波差分形式下的Maxwell 方程组中电场、磁场进行空间小网格化分解,该算法已经在耦合过电压研究中得到了广泛的应用。但由于其计算的是每个小网格电磁场,因此其计算耗时以及模型稳定性收到网格尺寸的影响,当网格尺寸设置过大,将无法反映真实的输电线路情况;而当网格尺寸设置过小,计算耗时较大,且稳定性程度较低。因此,本文采用“蛙跳格式”(leap-frog)二阶精确中心差分的形式对Maxwell方程组进行空间差分改进。
图1为二阶精确差分示意图。
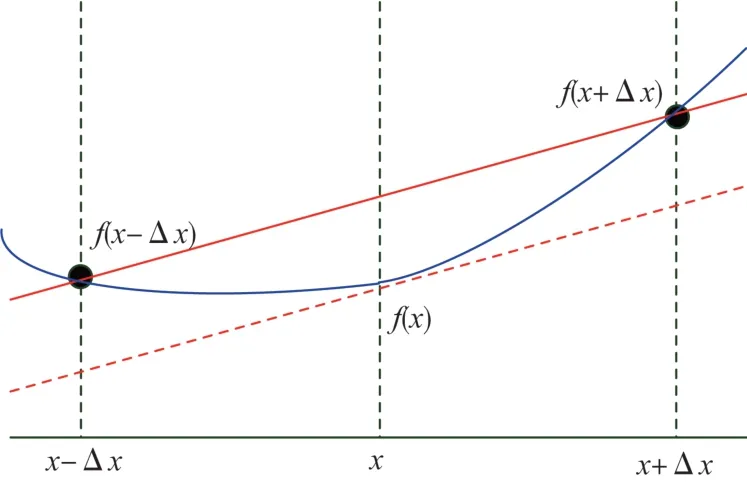
图1 二阶中心差分示意Fig. 1 Schematic diagram of second-order central difference
根据FDTD 网格划分的相邻格点电磁场,中心点位电磁场计算表达式二阶差分形式如式(4)所示。
式中:Δx为网格尺寸;f′(x)为计算差分;f(x)、f(x+ Δx)、f(x- Δx)分别为x、x+ Δx、x- Δx位置处的电磁场。
Maxwell向量旋度方程如式(5)所示。
式中:为电场矢量;为磁场矢量;∇为微分算子;t为时间;∂为求解偏微分;ε为相对介电常数。
可以得到直角坐标系下3 个标量电场与磁场关系模型如式(6)所示。
式中:Ex、Ey、Ez分别为直角坐标系x、y、z方向电场强度;Hx、Hy、Hz分别为直角坐标系x、y、z方向磁场强度;t为时间。
因此,根据上述式(4)、式(6),常规Maxwell方程组FDTD差分表达式如式(7)所示。
式中:Δy、Δz分别为y、z方向网格宽度;Δt为单位时间步长;n为迭代次数。
计算过程中为保证数值稳定性边界条件设置如式(8)所示。
式中:Δx为网格尺寸;c为雷电流传播速度;t为时间。同时空间尺寸设置为3 km×3 km,网格尺寸Δx取值为5 m,时间步长为5 ns。采用一阶Mur 吸收边界。
根据上述电磁场二阶差分形式,结合Agrawal耦合模型[25]可以计算出空间任意点位耦合雷电过电压峰值。
2 研究与分析
为研究多脉冲回击电流以及电晕放电效应对架空输电线路耦合过电压的影响,本文主要研究110 kV输电线路相线水平布设情况,具体结构如图2所示。
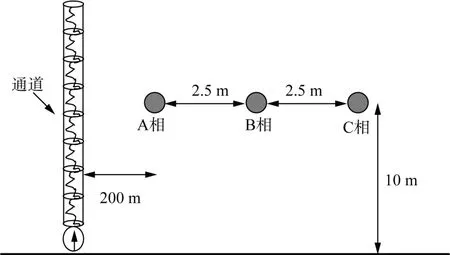
图2 输电线路相位水平布设方式示意图Fig. 2 Schematic diagram of phase horizontal layout of transmission lines
图2 中水平布设各相位水平间隔均为2.5 m,导线长度均为500 m,回击通道垂直于地面长度为8 000 m,且距离最近相位导线中点位置水平距离200 m 处,线路及杆塔阻抗取值150。激励电流源采用本文所建立的多脉冲及电晕放电效应模型,3次激励源峰值分别为20 kA、18 kA、16 kA,代表一次完成闪击放电过程,总耗时8 μs,计算结果如图3所示。
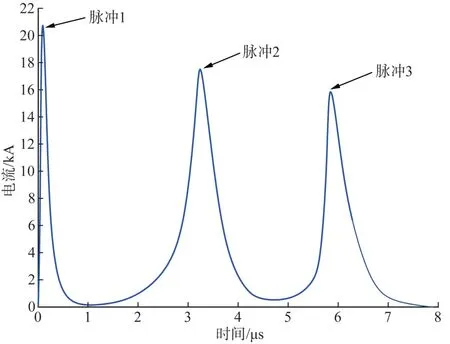
图3 多脉冲激励电流源波形Fig. 3 Waveform of multi-pulse excitation current source
2.1 多脉冲对耦合过电压的影响
本文首先研究多脉冲对线路耦合过电压的差异性,暂不考虑电晕放电效应,回击通道垂直于地面长度为8 000 m,且与A 相导线水平距离为200 m,线路及杆塔阻抗取值150,导线对地高度为10 m。分别计算在单脉冲、多脉冲以及IEEE 标准下的过电压变化趋势,其中单脉冲采用双Heidler 回击电流、多脉冲采用本文式(1)电流模型。
图4 为在单脉冲(峰值电流为20 kA)、多脉冲(3 个峰值电流)作用下输电线路A 相线耦合雷电过电压峰值变化情况。

图4 多脉冲、单脉冲对A相耦合过电压变化趋势Fig. 4 Changing trend of multi-pulse and single pulse to phase A coupling overvoltage
从图4 可以看出,多脉冲、单脉冲作用下输电线路同一个位置处耦合的雷电过电压存在较大差异性,同时本文计算出在单脉冲作用下的过电压峰值与IEEE 标准计算出的结果较为一致,峰值电压分别为99.5 kV、101.6 kV,相对误差为2.11%,说明了本文所建模型是准确的。
根据多脉冲显示结果,计算出的过电压峰值为116.5 kV,较单脉冲抬升了17.08%,而在实际的工作中忽略了多脉冲的影响,即弱化了17.08%峰值电压,这将导致输电线路无法进行准确的防雷设计。
2.2 多脉冲及电晕放电效应对过电压的影响
图5 为本文计算出在多脉冲作用下考虑电晕放电效应时输电线路A 相耦合雷电过电压峰值变化情况。可以看出,电晕放电效应对耦合过电压峰值存在一定的抑制作用,在电晕抑制作用下计算出的过电压峰值为108 kV,将未考虑电晕效应下的过电压峰值抑制了7.29%,这一结果与文献[13]指出在电晕的作用下可以使得线路耐雷水平提升4%~9%相接近。
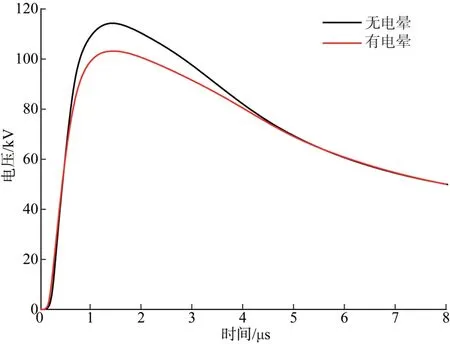
图5 多脉冲作用下电晕效应对过电压的影响Fig. 5 Influence of corona effect on overvoltage under multi pulse action
2.3 不同相位耦合过电压差异性
图6 为本文计算出在多脉冲以及电晕放电效应共同作用下输电线路A、B、C 三相耦合雷电过电压峰值变化情况,可以看出虽然3 个水平布设相位间隔较短,但耦合的过电压峰值仍存在较大差异,其中A、B 两个相位耦合过电压情况较为一致,而C 相导线耦合的过电压与其余两相差异性较大,与A 相过电压峰值相差17.5%,主要是因为雷电波传输至A 相线时,使得三相周围空间电场强度增强,多脉冲雷电波随着时间推移,使得较远处C 相导线电晕放电效应不断增强,电晕效应要高于其余两个相线,因此在C 相导线电晕效应对耦合过电压的抑制效应更加显著,从而导致了C 相导线耦合的过电压峰值与其余两个相位相差较大。
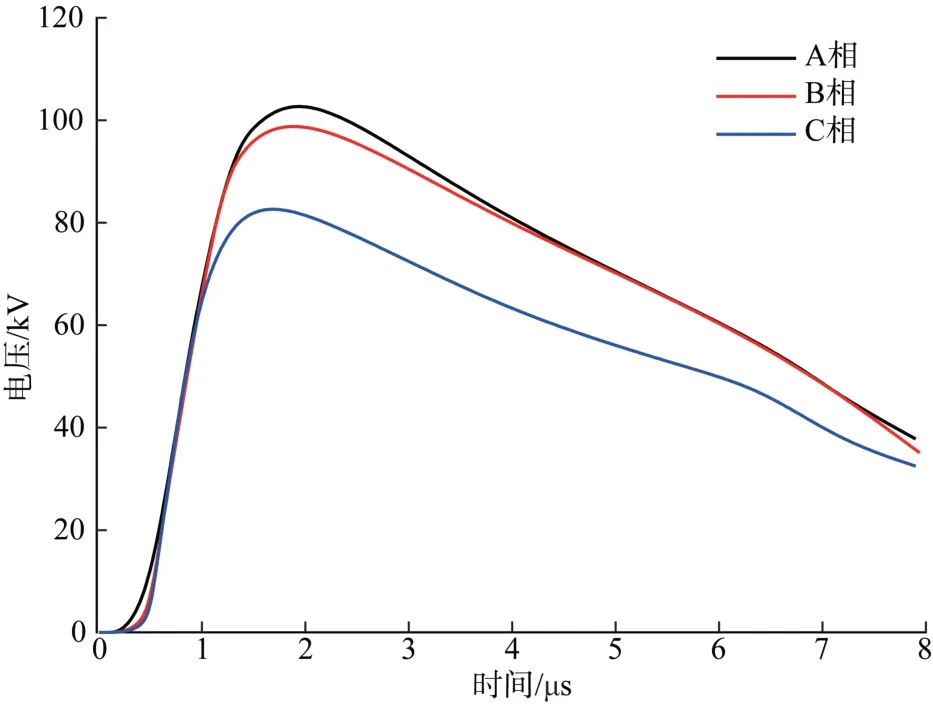
图6 多脉冲及电晕效应作用下不同相位耦合过电压Fig. 6 Different phase coupling overvoltages under multi-pulses and corona effects
3 结论
针对目前输电线路耦合雷电过电压研究工作中大多采用单一脉冲电流以及忽略了电晕效应抑制作用的现状。本文主要以双Heidler 回击电流为基础,建立了触发3 个回击电流峰值的多脉冲电流源,同时对传统电晕放电效应模型进行改进,结合FDTD算法,建立了更加精确的输电线路耦合过电压计算模型,得出结论如下。
1) 在单脉冲作用下本文计算出的过电压峰值与IEEE 标准计算出的结果较为一致,相对误差为2.11%,证明了本文所建模型的准确性。
2) 多脉冲使线路耦合过电压峰值较单脉冲提升了17.08%,电晕效应抑制了多脉冲作用下输电线路过电压峰值7.29%。
3) 与雷击点较远相位导线耦合的过电压峰值与离雷击点最近相线过电压相差17.5%。
