多直流馈入输电系统中高压柔性直流高频风险评估计算方法

李清，张东辉，陈名，周强，徐智华

（1. 中国南方电网有限责任公司超高压输电公司电力科研院，广州 510663；2. 清华四川能源互联网研究院，成都 610200；3. 中国南方电网有限责任公司超高压输电公司，广州 510663）

0 引言

柔性直流（简称直流）输电技术具有结构灵活、可控性高、输出谐波小、不发生换相失败等特点，具有较强的有功无功功率控制能力［1-3］。目前南方电网已建成鲁西背靠背直流、昆柳龙多端直流工程、大湾区中南通道背靠背直流等柔直工程。在柔直输电广泛应用的同时，也带来了高频谐振风险，如鲁西背靠背直流输电工程广西侧高频谐波谐振现象［4-6］、渝鄂柔直南通道渝侧接入交流电网产生的系统高频谐振等［7］。昆柳龙多端直流工程、大湾区中南通道背靠背柔直工程接入广东多直流馈入系统，近区有多回常规和柔直，高频谐振风险影响因素更为复杂，对柔直的高频谐振风险评估需要更为精确和谨慎［8-10］。

目前，柔直系统高频谐振分析方法可分为特征值分析法、时域仿真法和阻抗分析法。特征值分析法所研究的系统不能太大，适用于较小系统静态稳定性分析；时域仿真法适合作为辅助分析方法，用于快速分析或验证系统在不同扰动以及运行状态下的稳定性；阻抗分析法概念清晰，对振荡点的特性观测准确，适用于复杂系统的稳定性分析，但该方法受系统阻抗模型假设条件的影响较大［11-13］。在交直流高频谐振分析中目前应用得较多的是阻抗分析法，文献［14-16］基于阻抗分析法和奈奎斯特判据对交流系统稳定性问题进行了分析，同时通过时域仿真对风险结果进行复现和验证。从相关文献可以发现柔直是否会发生高频谐振现象不仅和柔直自身的宽频阻抗特性密切相关，也和外部系统宽频阻抗特性密切相关。文献［17-18］对柔直的阻抗特性进行了详细地解析推导，指出了影响柔直谐振特性关键因素。文献［19］介绍了基于直流详细的全电磁模型，采用测试信号法对直流谐波阻抗特性可以进行较为准确的分析和计算，该方法对于重点分析的直流来说是有必要的，但是对于含多回直流的系统谐波阻抗扫描来说，该方法由于需要多回直流详细的不同方式全电磁模型，效率偏低，必要性也需要进一步分析。在外部系统阻抗特性分析中NIMSCAN 软件是国内应用较广的计算软件，文献［20］介绍了浙江大学开发的交流系统谐波计算程序。文献［21］介绍了DIgSILENT谐波潮流计算模块计算交流系统阻抗的方法。已有外部系统阻抗特性分析基本只考虑交流线路、变压器、发电机、负荷等交流系统元件，近区其他多类型直流对柔直高频谐振风险影响研究相对缺乏。

本文针对单个柔直与外部系统高频谐振风险评估问题，首先介绍含多回直流等电力电子设备的交流外部系统谐波阻抗计算方法，考虑到系统内多回直流运行方式多、参数多、谐波阻抗特性获取复杂，详细计算效率低、必要性存疑的问题，引入衡量多直流馈入系统中各换流站间相互作用的强弱多馈入直流相互作用因子（multi-infeed interaction factor，MIIF）指标评估计算柔直外部系统谐波阻抗时需要详细考虑的直流，从而快速且较准确计算柔直外部系统谐波阻抗；最后，基于实际某多馈入直流省级电网数据对所提方法进行了准确性验证。本文所提方法可以为多直流馈入系统中柔直规划运行的高频风险分析及规避提供一种更加精准且快速有效的方法。

1 柔直与外部系统谐波谐振风险评估基础

本文采用阻抗分析法分析柔直与外部系统谐波谐振风险，目前获取直流系统宽频谐波阻抗特性的通用工程方法是频率扫描法（小信号测试法），该方法计及了直流系统控制、交直流交互影响等各种非线性因素的作用，将换流站在交、直流侧分别等效为一二端含源、非线性阻抗网络［19］，物理意义鲜明，较符合实测出的直流系统特性。因此，针对单一频率从交流换流母线看向直流系统时可以将直流系统看作一带阻抗和电流源的诺顿等值电路，柔直、常规直流、新能源等电力电子设备都可以作类似处理，并结合阻抗分析法分析谐波谐振风险。

1.1 柔直与外部系统谐波谐振风险判定模型

柔直与外部系统谐波谐振风险评估机理可以用图1 的等值电路进行说明，以柔直换流站交流换流母线为分界点，将柔直系统和交流侧系统视为两个独立端口。

图1 柔直系统和交流侧系统构成的阻抗网络示意图Fig. 1 Schematic diagram of impedance network composed of VSC-HVDC system and AC system

图1 中Żvsc为柔直系统的交流端口阻抗，İvsc为柔直换流器输出参考电流，Żs为柔直外部系统的戴维南等值阻抗，V̇s为柔直外部系统的戴维南等值内电势，V̇pcc为柔直与外部系统的分界点电压。

可推算出分界点电压公式为：

当柔直系统或交流侧系统阻抗条件发生变化时，Żs/Żvsc在某些频率点等于或接近-1，对应频率点存在较大的谐波谐振风险。定义奈奎斯特稳定曲线Ġst=Żs/Żvsc，根据奈奎斯特稳定性判据，当Ġst的频率—阻抗曲线在幅值大于0 dB区间由上向下净穿越(2k+ 1)π的次数大于由下向上穿越(2k+ 1)π的次数时，系统不稳定，其中为k为大于等于0的整数。

1.2 柔直与外部系统谐波谐振风险判定模型

在不考虑柔直近区直流时，柔直外部系统为纯交流电网，其谐波阻抗一般采用基于机电数据的谐波阻抗扫描工具计算（本文采用交流系统谐波阻抗计算软件Hiscan），这类计算工具的原理及步骤如下。

1） 建立交流系统各元件谐波阻抗模型，包括发电机、变压器、交流线路、负荷等元件谐波模型，其中，交流线路应采用适应宽频分析的模型，较好的方式是采用考虑分布参数效应的等效PI 模型，其宽频特性较PI模型更准确，同时结合考虑集肤效应修正中高频阻抗，可以较大地提高线路模型适用的宽频分析范围。

2） 根据机电仿真数据获取交流系统各元件基频阻抗参数和拓扑连接关系，结合谐波元件模型形成节点谐波导纳矩阵。

3） 综合采用节点编号优化、稀疏技术等手段提高计算效率，采用高斯消元法或LU分解法（将一个方阵分解为一个下三角矩阵（lower triangular matrix）和一个上三角矩阵（upper triangular matrix）的乘积的方法）求解节点谐波阻抗矩阵，各对角元即为节点谐波阻抗值。

2 多直流馈入系统外部谐波阻抗计算

2.1 考虑近区直流等电力电子设备的谐波阻抗计算方法

常见的柔直外部系统阻抗计算目前仅考虑交流元件，对直流、新能源等电力电子设备基本上直接忽略。然而国内大电网呈现为交直流混联状态，特别是多直流密集馈入的受端电网，直流通常直接接入高压电网，大部分情况下有必要考虑近区常规直流和柔直的影响［22］。

对于外部系统中各直流的影响，本文采用阻抗网络建模方法将直流系统的交流端口谐波阻抗和其他并联交流元件一样作为并联导纳元件注入到交流系统谐波阻抗扫描的导纳矩阵中，从而使谐波阻抗扫描计及了直流系统接入的影响。

对于一多直流馈入系统，其等值阻抗网络如图2所示，利用节点法可形成节点导纳矩阵[Yn]。

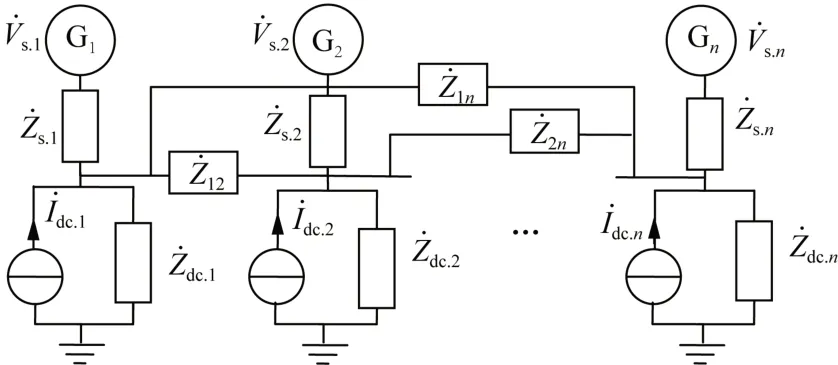
图2 多直流馈入系统阻抗网络示意图Fig. 2 Schematic diagram of Impedance network of multiinfeed DC system

采用矩阵求逆得到[Zn]=[Yn]-1，从而完成多直流馈入系统谐波阻抗计算。

2.2 多直流间电气距离对谐波阻抗的影响

根据各直流换流站间分布的位置差异分为以下两种情况。

1） 柔性直流和常规直流接入点相同，如图3所示，柔直站点等值阻抗Ż和分界点电压V̇pcc为：

图3 柔性直流和常规直流接入点相同示意图Fig. 3 Schematic diagram of VSC-HVDC and LCC-HVDC are connected to the same location

式（3）—（4）中，Żhvdc为常规直流系统的交流端口阻抗，İhvdc为常规直流换流器输出参考电流，其他符号含义与图1中一致。

根据式（3）—（4），此时常规直流系统阻抗直接与柔直系统阻抗和交流侧系统阻抗并联，对柔直站点等值阻抗影响较大，不能忽略直流影响。当按照式（1）分析谐振时，常规直流系统阻抗可并入交流系统侧，也可并入柔直系统侧。

2） 柔性直流和其他直流接入点不相同，如图4所示，柔直站点等值阻抗Ż为：

图4 柔性直流和常规直流接入点不相同示意图Fig. 4 Schematic diagram of VSC-HVDC and LCC-HVDC are connected to different location

式中：Żs.1为柔直并网点自阻抗；Żs.1为常规直流并网点自阻抗；Ż12为常规直流与柔直之间的互阻抗；V̇s.1为柔直并网点自阻抗后面的等值内电势；V̇s.2为常规直流并网点自阻抗后面的等值内电势，其他符号含义与式（4）中一致。

根据式（5）可知，直流系统间的互阻抗Ż12越小，根据并联关系，其他直流对柔直站点阻抗影响越大，当直流系统间的互阻抗越大，其他直流对柔直站点阻抗影响越小。因此，理论上来说，忽略电气距离较远的直流系统对柔直站点阻抗计算影响较小。

3 柔直外部系统谐波阻抗实用计算方法

实际中柔直和常规直流的阻抗模型相对较为复杂，可以采用理论近似计算，也可以对电磁暂态模型进行测试信号法或实测的方法得到其外特性阻抗模型。另外，柔直的阻抗特性和其运行点关系较小，主要与关键控制参数强相关，常规直流阻抗特性和运行点关系较大，且容易受测试信号法注入谐波源影响［14］，因此，实施测试信号法时应尽可能避免或仅考虑主要影响因素并进行去复杂化处理。本文引入相互作用因子（multi-infeed interaction factor，MIIF）指标量化各直流站点间的电气距离，判断需要考虑的直流系统谐波阻抗特性，提出柔直外部系统谐波阻抗实用计算方法［23-26］。

3.1 MIIF量化指标定义

MIIF 定义为：在交流母线i上通过人为并联一个电抗元件，使得母线i上产生一个1%的突变电压 ΔUi，观察母线j上电压变化的比例ΔUj，这两个电压变化的比值即为多馈入交互作用因子MIIF，其值记作iMIIF，如式（6）所示。

由定义可得，如果两个换流站母线之间的距离无穷远，则iMIIF= 0；如果两个换流站连接到同一个上母线，则iMIIF=1；对于工频50 Hz，iMIIF的范围在0~1 之间，电气距离相隔越远，iMIIF越接近于 0，电气距离相隔越近，iMIIF越接近于 1；对于谐波频率段，电力电子等非线性设备无法保证无源性，因此iMIIF可能大于1。

本文直接引用文献［23］中基于阻抗法推导的iMIIF计算公式如式（7）所示，其计算精度较高，即iMIIF等于互阻抗和自阻抗的比值。

式中：Żii为节点i的自阻抗；Żij为节点i与节点j之间的互阻抗。

3.2 柔性直流和常规直流阻抗特性分析

从交流系统侧来看，常规直流包含换流变、换流器以及滤波器部分，MMC 类型高压柔直一般没有滤波器，只有换流变和换流器部分。常规直流和柔性直流的交流端口谐波阻抗一般采用频率扫描法获取，典型的方法是采用频率扫描获取从交流换流母线看向直流系统的谐波阻抗，因此，常规直流注入的阻抗特性为常规直流交流端口阻抗与滤波器阻抗的并联，柔性直流注入的阻抗特性为柔性直流交流端口阻抗。

采用国内实际1×3 000 MW 常规直流PSCAD 模型和2×1 500 MW 柔性直流PSCAD 模型进行频率扫描，得到常规直流和柔性直流的交流端口阻抗（从换流站交流换流母线看向直流侧的等值阻抗）曲线如图5—6 所示，本文采用频率扫描的直流系统交流端口阻抗在下文用于实际案例的谐振风险点分析，谐振风险点分析结果与时域仿真谐振频率吻合，证明了直流系统交流端口阻抗扫描结果的准确性。对应的常规直流滤波器谐波阻抗曲线如图7所示。

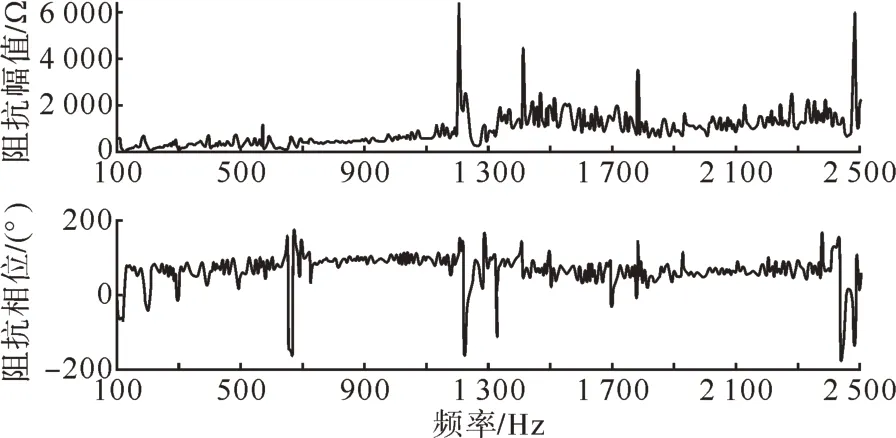
图5 典型常规直流换流器（不含滤波器）交流端口阻抗Fig. 5 Typical AC port impedance of LCC-HVDC converter（filters excluded）

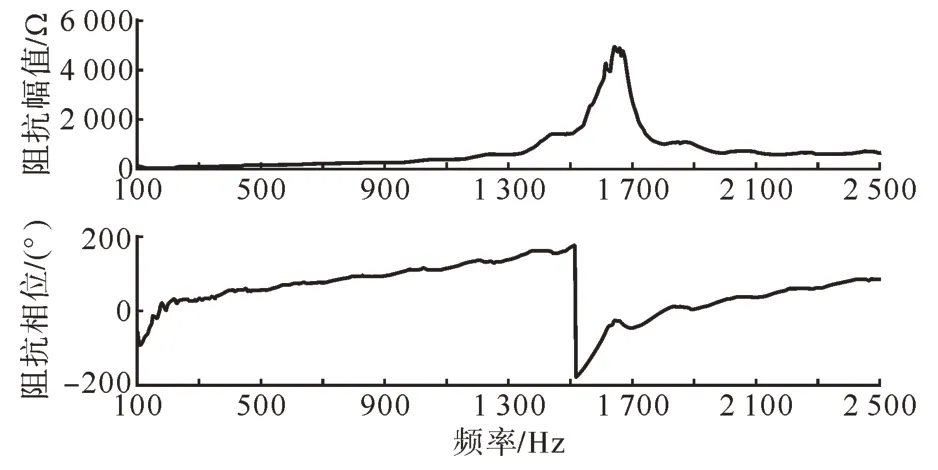
图6 典型柔性直流交流端口阻抗Fig. 6 Typical AC port impedance of VSC-HVDC

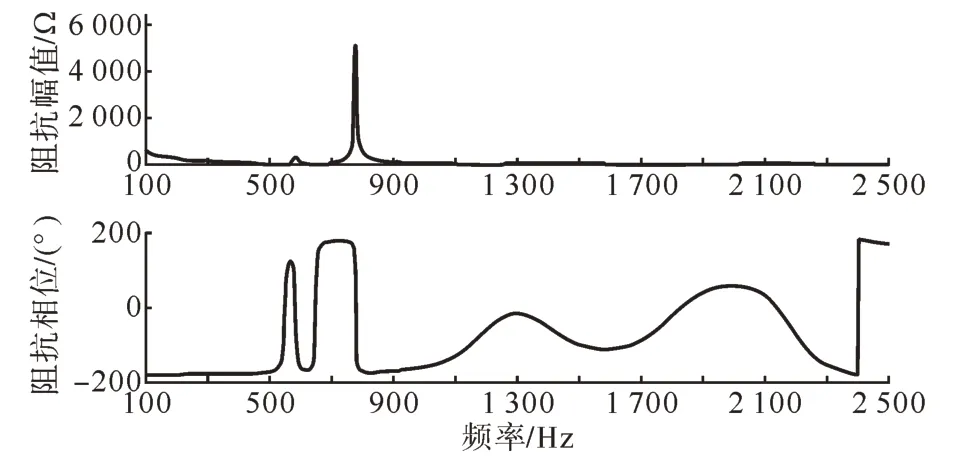
图7 典型常规直流滤波器阻抗Fig. 7 Typical impedance of LCC-HVDC filter

由图5—6 可知常规直流和柔性直流的交流端口阻抗幅值在中、高频段较大，对交直流系统谐波阻抗特性通常影响较小，但应防止发生满足奈奎斯特判据的谐振现象。

由图7 可知常规直流滤波器部分在中高频段谐波阻抗幅值较小，如果多组滤波器一起投入，则并联后谐波阻抗更小，因此对交直流系统谐波阻抗特性通常影响较大，一般不可忽略。

3.3 柔直外部系统谐波阻抗实用计算方法

为判断直流是否对谐波阻抗影响较大，本文采用iMIIF指标量化评估各直流站点间相互影响的强弱。工频的iMIIF越小，电气距离越远，在高频段会有频率放大作用，一般高频电气距离或相互影响会更小，为简化考虑，可以用工频iMIIF作为衡量高频段电气距离的工具。具体分为以下3 种情况：1）当iMIIF<μ1时，表明电气距离相对较远，计算时可以不考虑常规直流和柔性直流的影响；2）当iMIIF在μ1~μ2之间时，表明电气距离相对较近，常规直流和柔性直流的换流变和换流器本体谐波阻抗部分可以忽略，但需考虑常规直流滤波器的影响；3）当iMIIF>μ2时，表明电气距离很近，需要详细考虑直流阻抗特性。计算流程如图8所示。

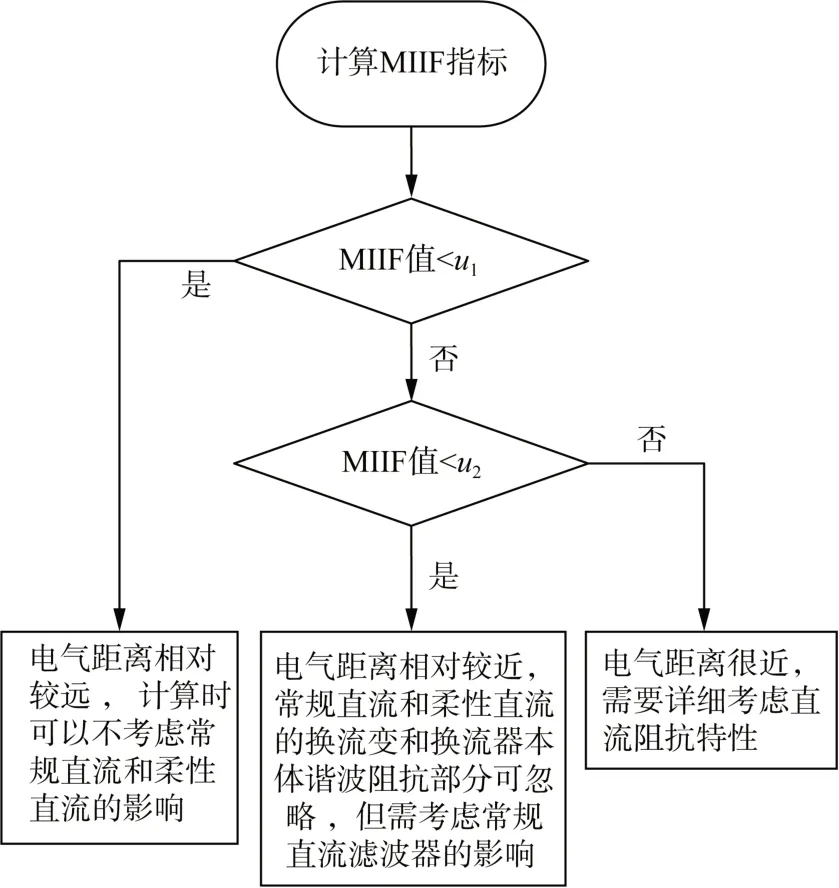
图8 柔直外部系统谐波阻抗实用计算方法Fig. 8 Practical calculation method of harmonic impedance of VSC-HVDC external system

4 案例分析

本文基于实际某多馈入直流省级电网数据，该电网有两个背靠背柔性直流换流站（柔直Z、柔直N），同时近区还有多回常规直流和柔性直流馈入，包括WDD 柔直、CS 直流、NC 直流、TG 直流、GZ 直流、XD 直流，建立该多馈入电网BPA 模型和PSCAD全电磁模型。柔直Z、柔直N附近直流接入情况如图9所示。

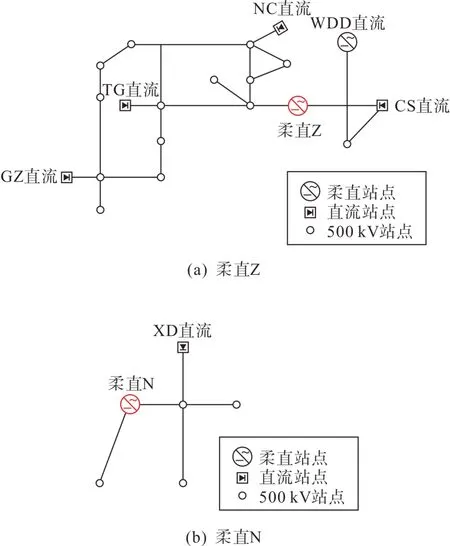
图9 柔直Z、N附近直流接入情况示意图Fig. 9 Schematic diagram of DC access in the near area of VSC-HVDC-Z and VSC-HVDC-N

基于BPA 模型，利用谐波阻抗扫描软件HISCAN 计算出各直流站点的自阻抗和站点间互阻抗，根据式（7）计算出iMIIF，如表1所示。

表1 各直流站点间iMIIFTab. 1 iMIIF between every two DC stations

采用本文提出的柔直外部系统谐波阻抗实用计算方法，以设定阈值μ1=0.35 和μ2=0.7 为例（阈值越大，需要考虑的近区直流越多，计算越复杂，准确性越高），计算柔直Z 和柔直N 外部系统谐波阻抗时仅需要考虑CS、NC、TG、XD 共4 个直流逆变站的滤波器阻抗，以及CS 直流换流变和换流器阻抗。相较于详细考虑所有常规直流和柔性直流的换流变和换流器阻抗，实用计算方法可以大大减小工作量。

分别计算3 种方法下柔直Z、N 各站点100~2 500 Hz谐波阻抗，如图10所示。

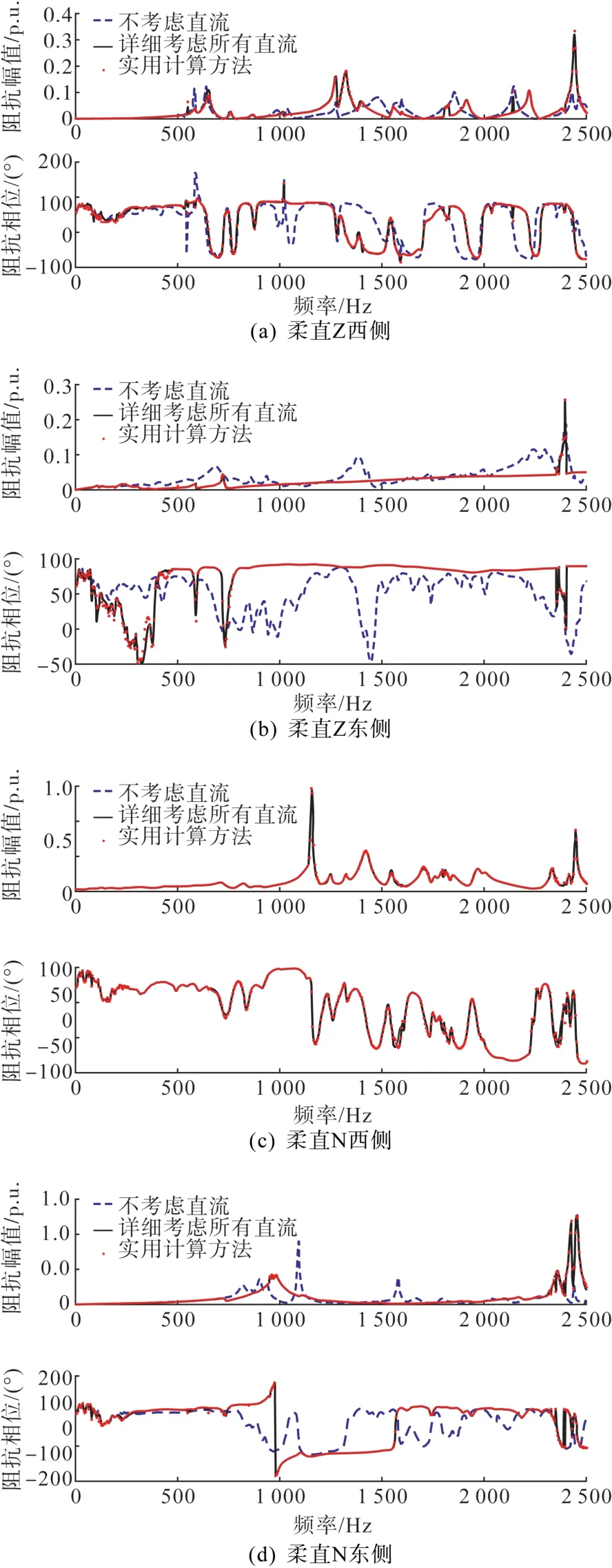
图10 3种计算方法下柔直Z、N各站点谐波阻抗比对Fig. 10 The harmonic impedances of VSC-HVDC Z and VSCHVDC N sites under three calculation methods

方法1：不考虑直流影响，忽略直流系统阻抗；

方法2：详细考虑所有常规直流和柔性直流的换流变和换流器阻抗，以及常规直流滤波器阻抗；其中，各个柔直、常规直流的换流变和换流器本体谐波谐波阻抗基于频率扫描法获取，频率扫描法在通用电磁暂态仿真软件EMTDC/PSCAD 平台上实施。

方法3：采用本文提出的柔直外部系统谐波阻抗实用计算方法。

3 种方法下柔直Z、N 各站点谐波阻抗比对如图10 所示。3 种计算方法中方法1 计算较为粗糙，方法2 计算最为准确，方法3 即本文所提方法。由图10 可见，方法1 与方法2 阻抗扫描结果差别较大，本文所提方法3 与方法2 阻抗扫描结果基本一致，误差统计如表2 所示，不考虑直流时平均误差普遍较大，采用本文提出的快速实用计算方法时，平均误差<5%，阻抗特性与详细考虑所有直流时基本一致。因此，本文提出的柔直外部系统谐波阻抗实用计算方法可以兼顾精度和效率，可以适用于实际交直流混联大电网谐波阻抗综合扫描。

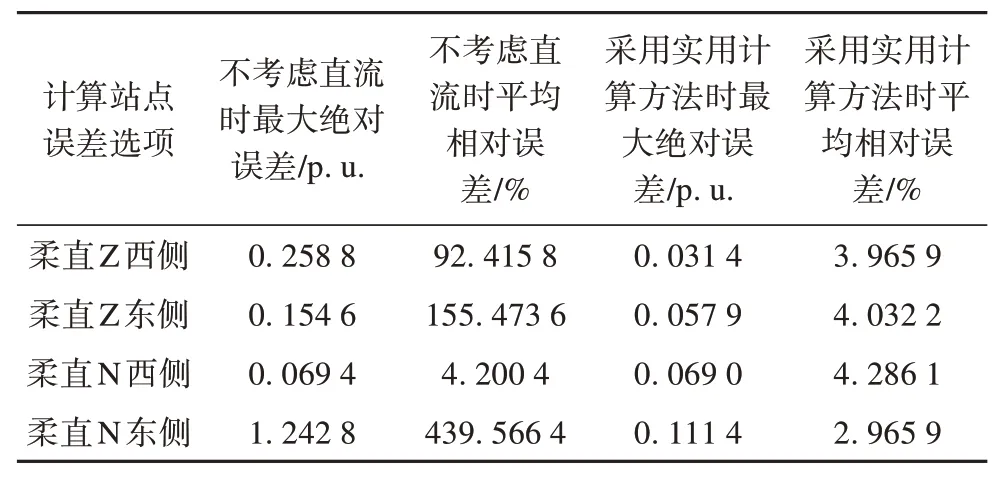
表2 不考虑直流和实用计算方法误差统计Tab. 2 Error statistics of without considering DC system and practical calculation methods

为了验证本文方法用于分析高频谐振风险的有效性，以柔直N 东侧为例将谐波阻抗实用计算方法阻抗扫描结果应用于分析交直流高频谐振风险，在交流系统全接线方式下柔直外部系统阻抗Żs与柔直N 东侧阻抗Żvsc比的波特图如图11 所示，依据奈奎斯特判据计算得出的谐振风险频率约为990 Hz，相角裕度为-20.08 °；PSCAD 时域仿真成功激发谐振，柔直交流母线电压电流波形如图12 所示，系统发生严重谐波放大现象，电压电流波形FFT 分析结果如图13 所示（图中没有显示工频分量），谐振频率为937 Hz，与奈奎斯特判据分析结果较为接近，证明了谐波阻抗扫描对高频谐振风险分析的可靠性。

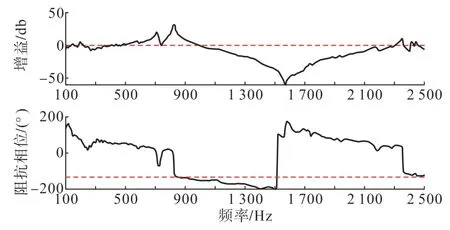
图11 柔直外部系统阻抗与柔直N东侧阻抗比值Fig. 11 The ratio of the impedance of VSC-HVDC external system and east side impedance of VSC-HVDC N

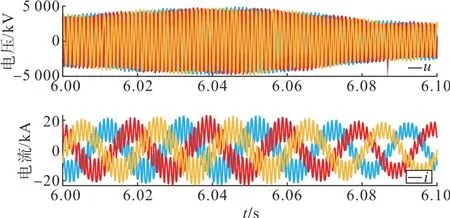
图12 柔直交流侧母线电压电流波形Fig. 12 Voltage and current waveforms of VSC-HVDC AC side bus

图13 电压电流FFT结果Fig. 13 Voltage and current FFT results

采用本文提出的柔直外部系统谐波阻抗实用计算方法，可以大大提高柔性直流高频风险分析工作的效率，以本文采用的实际案例来说：1） 相比详细考虑所有常规直流和柔性直流的换流变和换流器阻抗（需要收集外部系统6 条直流的详细电磁模型数据），采用本文提出的柔直外部系统谐波阻抗实用计算方法时仅需要收集CS 直流详细电磁模型数据，以及NC、TG、XD这3个直流逆变站的滤波器配置数据，可以大量减小直流模型数据收集的时间和难度；2）在采用电磁模型仿真验证阶段也可以同步去掉不需要考虑的直流模型，可以提高电磁模型的仿真速度，特别是在需要批量计算的场合，可以较大程度提高工作效率。

5 结论

本文就评估柔直与外部系统发生谐波谐振风险总结出一般方法，并基于阻抗分析法原理提出含多回直流等电力电子设备的交流外部系统谐波阻抗计算方法。同时，为了应对实际大网系统内多回直流在多种运行方式下谐波阻抗特性获取复杂以及详细计算难度大、效率低、必要性存疑等问题，本文引入iMIIF指标用以评估计算柔直外部系统谐波阻抗时需要详细考虑的直流系统，理论上可以快速且较准确地计算柔直外部系统谐波阻抗。经过实际某多馈入直流省级电网数据建立的BPA 模型和PSCAD 模型进行仿真验证，成功证明了所提的柔直外部系统谐波阻抗实用计算方法准确度高、速度更快，所分析出的谐振风险频率与PSCAD 时域仿真结果吻合。因此，本文所提方法可以为多直流馈入系统中柔性直流规划运行的高频风险分析及规避提供一种更加精准且快速有效的方法。