基于BP神经网络的内陆水库水深反演★

周 彬，何清平，何 林，林国敏，邓仕雄，刘继庚，邹 宇

(1.贵州水利水电职业技术学院,贵州 贵阳 551416; 2.贵州盘江煤电集团技术研究院有限公司,贵州 贵阳 550081)

0 引言

目前绝大多数生产单位都是使用单波束或多波束等船载传感器来获取水深,虽然这种传统手段获取的水深精度在目前相对较高,但也存在不少弊病,在大面积水下地形测量时成本急剧增加,在船只不能到达的敏感区域无法进行水下测量,在水下地形不熟悉的区域还存在触礁沉船等安全风险,因此,传统手段在人力、物力和财力方面存在不足。

随着遥感技术的发展,其在各行各业的应用越来越广泛,遥感水深反演成为可能。国外学者Lyzenga根据水体本身的性质进行了研究,发现对数线性模型反演效果相对较好,但受水质和底质的影响较大。Figueiredo在对数线性模型中加入与水质和底质有关的参数,提高了模型反演精度,但也增加了模型的复杂程度,且实际生产中这些参数较难获取。

计算机技术的发展让机器学习算法开始崛起,不少学者将其应用到遥感水深反演领域,并得到较好效果,其中,BP神经网络就是其中之一。2005年,王艳姣采用BP神经网络对长江口南港水下地形进行反演,发现水深小于5 m的区域反演效果更好[1];2006年,徐升发现BP神经网络模型反演效果比单波段模型、多波段模型、比值模型的精度要高[2];2008年,闫峰把泥沙因子引入到BP神经网络模型,发现该模型可削弱悬浮泥沙对遥感水深反演的影响[3];2012年,梁志诚等发现BP神经网络具有很好的自适应学习能力和非线性映射能力,在处理遥感水深反演的问题上比传统方法有更高的精度[4];2015年,樊彦国等通过对比发现,具有很好的自适应能力和非线性映射能力的BP神经网络模型在处理遥感水深反演问题上比传统的线性模型效果更好[5];2017年,曹斌等对BP算法进行改进,改进后的BP算法训练迭代收敛速度明显快于传统BP算法,浅水区的水深反演精度优于传统BP算法[6]。

基于上述研究,本文拟采用BP神经网络模型对三角海水库研究区水深进行反演,并与传统水深模型中的对数线性模型进行对比分析,以验证BP神经网络模型在内陆水库水深反演的适用性。

1 研究区概况

三角海水库位于云南省红河哈尼族彝族自治州开远市羊街乡西部鱼塘寨村,地理位置为东经103°18′、北纬23°34′,距离羊街乡集镇6 km。开远市三角海水环境综合治理工程范围北至三角海水库西坝-北坝沿线,南至三角海南坝,西至三角海西岸,东至大庄河入湖口-鱼塘寨-湖湾区一带,红线面积约8.47 km2(含三角海水库水域面积4.33 km2),研究区范围如图1所示。

2 数据源及数据预处理

研究区航飞影像数据于2020年5月30日拍摄,本项目UAV航空摄影飞行平台采用飞马F200智能航测系统,相机参数如表1所示。

影像数据经过辐射定标、大气校正、地理配准等数据预处理后,再在遥感软件中进行进一步处理,即可获取所有水深点对应的波段信息,考虑到水底底质和水质存在空间差异性,将地理位置和波段辐亮度一起作为模型的输入。

本次水下地形测绘采用GNSS RTK+测深仪的高精度组合测深系统施测。水深数据采集与无人机影像采集同步进行,水面高程可采用GNSS RTK测量得到。数据采集后经过各项改正和检查后获得水下高程点,水深数据可根据水下高程和影像获取当日GNSS RTK实测水面高程推算。该研究区水深数据经过处理后获得1 603个水深点,水深范围为0.1 m～4.6 m,随机选取总点数的70%作为训练点,剩下的30%为测试点。

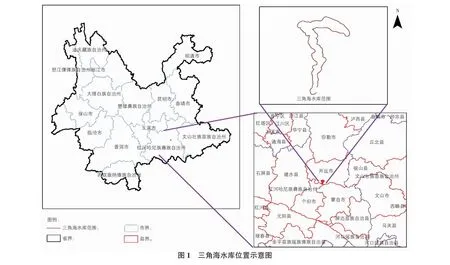
表1 相机参数

3 模型和评价指标

3.1 BP神经网络模型

BP神经网络是一种非线性多层前向反馈网络,分为输入层、隐含层和输出层共三层,这三层按照次序只能是上一层对下一层产生影像,当预测值和期望值之间存在较大差异时,网络将差异值反向传播,直至预测值精度满足要求则停止传播,BP神经网络结构如图2所示。

采用BP神经网络进行水深反演的具体思路是:输入包含波段信息和地理位置信息的遥感数据,利用隐含层对网络的权值和阈值不断地进行计算、调整和训练,当预测水深值和实测水深值之差在设置的误差阈值范围内时,输出该预测水深值到输出层。通过不断尝试,确定模型中隐含层层数为1,隐含层节点数设置为12,隐层函数选择sigmoid,输出函数选择purelin。

3.2 评价指标

采用平均相对误差(MRE)和相关系数(R)2个指标对水深反演结果进行评价。

平均相对误差是相对真实水深而言的,当平均绝对误差越小,这个指标就越小,表明反演结果越好。平均相对误差的计算公式如式(1)所示:

(1)

相关系数是反演水深值和真实水深值之间的相关程度,相关系数越大,表示反演水深值和真实水深值相关性越好,反演结果越好。相关系数的计算公式如式(2)所示:

(2)

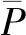
4 结果分析

为分析BP神经网络模型的反演精度,将反演结果与多波段对数线性模型的评价指标进行比对,如表2所示。从表2可以看出,多波段对数线性模型的平均相对误差为33.8%,而BP神经网络模型的平均相对误差为20.8%,较多波段对数线性模型提升了38.5%;多波段对数线性模型的相关系数为0.513,而BP神经网络模型的相关系数为0.924,较多波段对数线性模型提升了80.1%。由此可得,从评价指标上看,BP神经网络模型明显优于多波段对数线性模型。

表2 模型指标对比统计表

为更直观的反映BP神经网络模型的反演精度,可绘制多波段对数线性模型和BP神经网络模型的实测水深-反演水深散点图,如图3所示,图3(a)是多波段对数线性模型的实测水深-反演水深散点图,图3(b)是BP神经网络模型的实测水深-反演水深散点图。图中x轴表示实测水深,y轴表示反演水深,y=x这条斜线表示实测水深与反演水深相等的曲线,其意义在于,点位越靠近这条曲线,表示反演水深与实测水深越接近,绝对误差越小,反演结果越好。

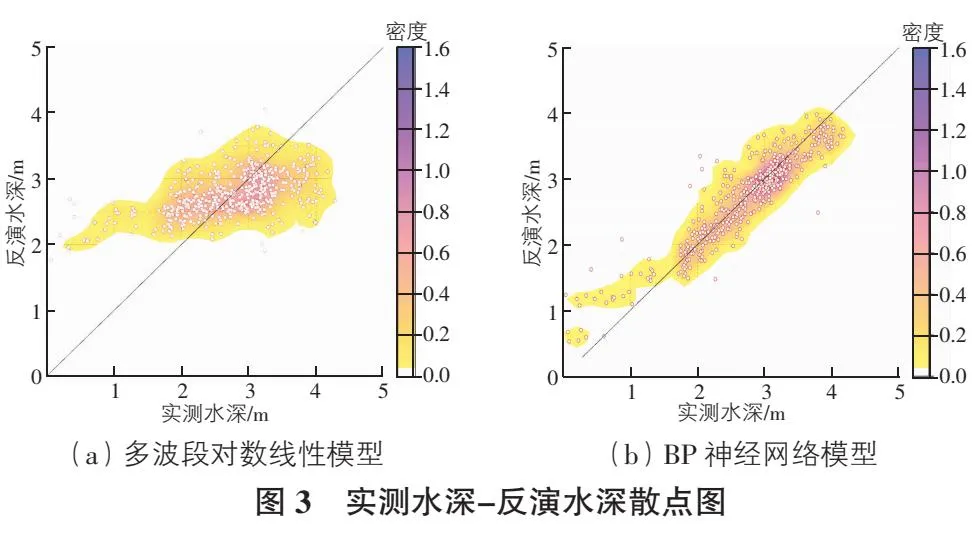
从图3(a)可以看出,多波段对数线性模型在0 m～2.5 m反演水深值总体偏大,在2.5 m～4.5 m反演水深值总体偏小,且总体实测水深点和反演水深点较为离散。从图3(b)可以看出,BP神经网络模型在0 m～1.5 m反演水深值总体偏大,在1.5 m～4.5 m反演水深值大体上一半偏大一半偏小,且总体实测水深点和反演水深点与y=x曲线接近。由此可得,从实测水深-反演水深散点图上看,BP神经网络模型明显优于多波段对数线性模型。

5 结论

首先,研究方法上,不管是从评价指标,还是从实测水深-反演水深散点图来看,BP神经网络模型反演精度明显优于多波段对数线性模型,这说明以机器学习模型为代表的BP神经网络模型在遥感水深反演的精度上,要优于以多波段对数线性模型的传统数学模型。其次,研究对象上,本文研究区为内陆水库,这表明BP神经网络模型除了适用于浅海和湖泊等研究区的水深反演外,在内陆水库水深反演同样具有一定的适用性。再次,研究水深方面,本文研究区水深小于5 m,属于极浅研究区,水深超过1.5 m时BP神经网络模型反演效果较好,这说明BP神经网络模型在极浅研究区同样具有一定的适用性。