内外流作用下的U型管流致振动分析

王骏，李 鹏，王麒均

（西南交通大学力学与航空航天学院，成都 611756）

引言

作为在生产中占据主导地位的换热设备，管壳式换热器已广泛地应用于化工、石油、能源、食品等多种工业生产中[1]。U型换热管作为冷、热两侧流体的分隔屏障及换热通道，会受到内、外流体的冲刷而发生流致振动现象，进而会影响设备的安全和稳定运行。

对于U 型换热管的流致振动问题，已有学者开展了相关研究。Lesmez等[2]基于传递矩阵法对充液U 型管的固有频率进行了研究。吴江海等[3]和王世忠等[4]采用梁理论研究了流体质量、流速等对管道固有频率的影响规律。庞天照等[5]采用流固耦合方法分析了外流作用下的单根U 型管的振动特性，获得了外激力对管道振动的影响规律。刘丽艳等[6-7]采用多孔介质模型研究了蒸汽发生器传热管所受外流湍流激振力分布情况，并在此基础上分析了不同约束方式下传热管的流致振动及磨损特性。朱磊[8]采用流固耦合方法对充液管道的预应力模态进行了分析，得到了不同充液压强对管道模态频率的影响规律。张杰等[9]采用流固耦合方法，对U 型充液管的充液过程进行了仿真，分析了充液过程及充液后管道的振动规律。施卿海等[10]采用实验方法，对受横向水流冲刷下的管束进行了研究，得到了不同流速下管束流体诱导的振动特性。周岩[11]和张宇祥等[12]分别对水平及竖直U 型管在不同流型及速度下的管内两相流诱导管道振动特性进行了研究。康竞澜等[13]采用计算流体动力学方法对受段塞流冲击的弯管受力特性进行了分析。俞树荣等[14]和谌冉曦等[15]基于ANSYS Workbench平台对输流弯管的流固耦合振动特性进行了研究。

上述研究大多仅单独考虑管外流体或管内流体作用下的U 型管流致振动特性，同时考虑两者联合作用的研究相对较少。事实上，内、外流体力的性质及其对U 型管流致振动的影响是不同的。因此，本文将计算不同内、外流速组合下U型管的流致振动响应，探究内、外流对管道振动的耦合作用机制以及不同流速下振动特性的变化规律。

1 计算模型及计算方法

1.1 计算模型

以汽水分离再热器为研究对象，其特点为U 型管受横向气流冲刷，管内流动液体为水。结合文献[5]，建立了有限空间内U 型管内、外流场计算模型，如图1 所示。图1 中，外流计算域左侧（红色）壁面为入口，右侧（蓝色）壁面为出口，其余壁面为无滑移壁面；内流计算域左侧（黄色）为入口，右侧（绿色）为出口。各部分尺寸见表1，管内、外流体及U型管材料（不锈钢）参数分别见表2、表3。

表1 计算模型尺寸 mm

表2 流体材料参数

表3 管道材料参数

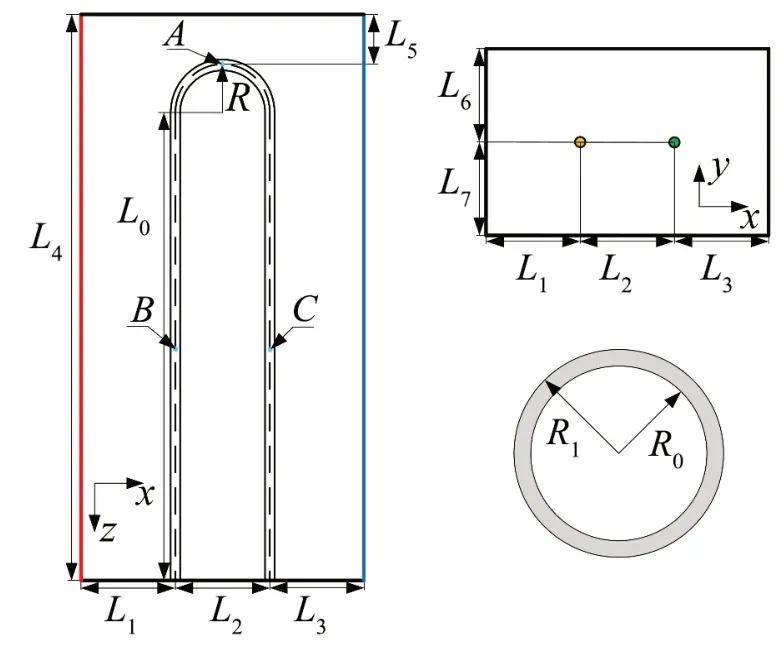
图1 计算模型

在ICEM CFD 中建立内、外流场的拓扑结构并进行六面体网格划分，对U 型管管壁附近网格进行加密处理，如图2所示。

图2 计算网格局部加密

分别建立3套不同数目的网格进行网格无关性验证。外流以vout=10 m/s 时的阻力最大值CD,max为验证指标；内流以vin=10 m/s时的U型管z方向所受合力Fz为验证指标，外流、内流网格无关性验证结果分别见表4、表5。为兼顾准确性与计算效率，本文以下计算中内、外流均选用第2套网格。

表4 外流网格无关性验证

表5 内流网格无关性验证

1.2 计算方法及有效性验证

本文采用单向流固耦合方法[16-17]计算U 型管的流致振动问题。选择以广义坐标x(t)（如结构有限元节点位移）对U型管进行建模。一般地，在流体力作用下的运动方程可表示为[16]：

其中，x(t)为节点位移为节点速度,为节点加速度，M为考虑管内流体附加质量的U 型管质量矩阵，C为U 型管阻尼矩阵，K为U 型管刚度矩阵，Fin(t)和Fout(t) 分别为内、外流体作用力。基于软件实现本文计算的流程如图3所示。

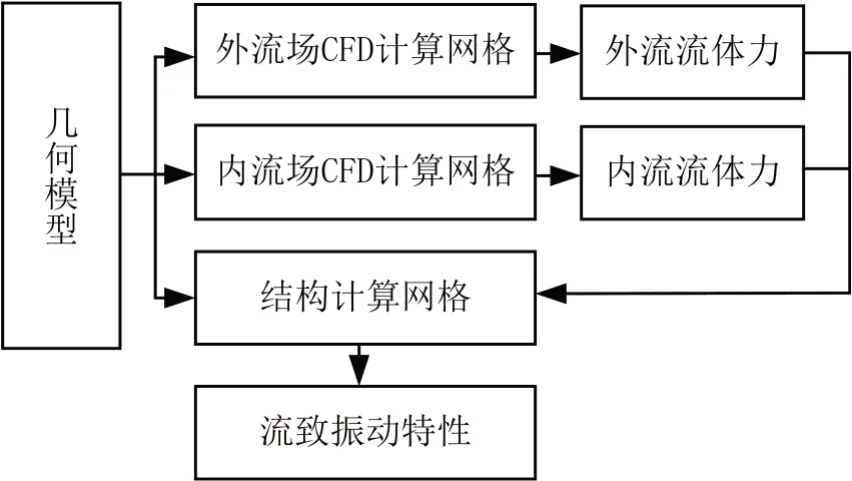
图3 计算流程图

为验证单向流固耦合方法用于计算U型管流致振动问题的有效性，首先采用该方法对文献[5]进行复现。流场计算部分复现结果与本文对比如图4(a)所示，结构响应部分复现结果与本文对比如图4(b)所示。复现结果表明，本文采用的单向流固耦合方法可以较好地计算此类问题。

图4 文献复现结果对比

2 流场分析

2.1 外流场分析

选取U 型管中间截面（图1中B-C截面）进行外流场分析，结果如图5 所示。由图5 可见，不同流速下流场涡结构分布规律类似，U型管上、下游两管之间存在着约1.5 对涡脱，外流体力为典型的涡脱激振力。

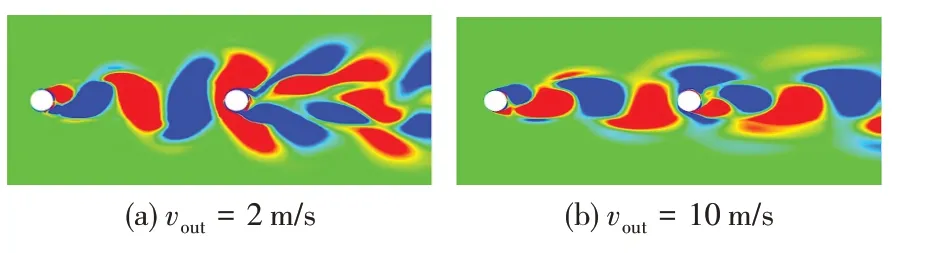
图5 B-C截面涡量图

图6 所示为U 型管所受流体力时程曲线，图中可见，用于流致振动计算的稳态升力、稳态阻力的振幅及频率随外流流速增大而增大。

2.2 内流场分析

充分发展后的内流对管道的作用相当于施加在管道内壁面的“静载荷”，无明显脉动现象，这与文献[9]中的结论一致。图7所示为U 型管在不同内流流速下的受力情况。由图7可见，入口段直管（编号1）、弯管段（编号2）及出口段直管（编号3）3 部分受力在x、y、z3 个坐标轴的投影分量的正负号并不相同。U 型管主要受力方向为z向（直管段轴向），z向受力又由弯管段主导，这是流体流经弯管时流动方向改变导致的。

3 流致振动分析

采用如下密度修正公式考虑静水对U型管的附加质量影响：

其中，ρ为修正后U 型管密度，ρin为管内流体密度，ρs为U 型管材料密度，参数值见表2、表3。S1为管内过水断面横截面积，S2为U 型管管壁横截面积。本文忽略不同工况下动水对U 型管的附加质量影响。由于管外绕流空气密度较低，也忽略管外流体对U型管的附加质量影响。U型管约束方式为出口及入口处固支约束。

3.1 模态分析

首先对U型管进行模态分析。空管（干模态）与充液管（湿模态）前6 阶固有频率对比见表6。由表6 可见，管内流体的附加质量降低了U 型管的固有频率，随模态阶数增加，影响比例基本不变。这与文献[18]中采用附加质量法对比空管与充液管模态的结果一致。

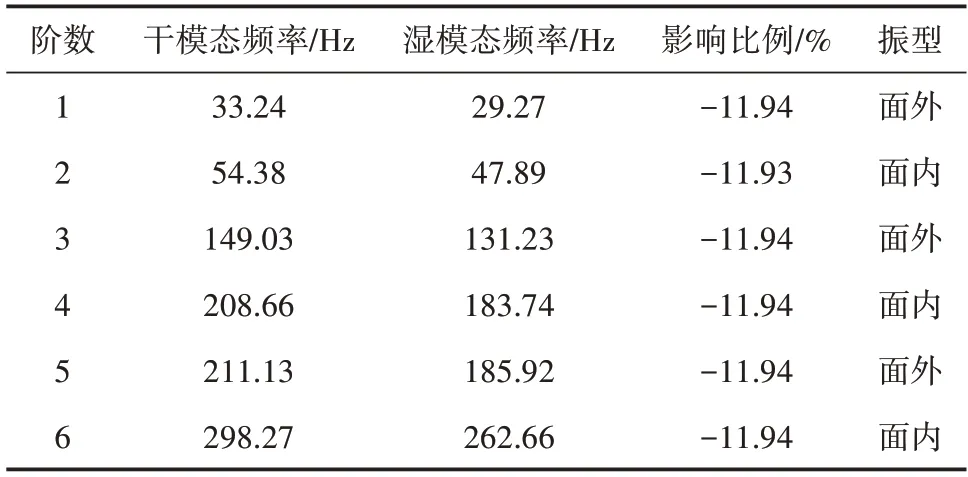
表6 U型管干、湿模态频率对比

3.2 振动响应分析

由于内、外流体力作用方向存在差异，采用振幅与频率的表述方式无法直观展示内、外流共同作用下U 型管的振动规律，因此本文采用平均位移与位移峰峰值的表述方式分析U 型管的流致振动响应。平均位移与位移峰峰值的定义方式如图8 所示，即振幅=平均位移+1/2位移峰峰值。

图8 平均位移及位移峰峰值示意图

不同内、外流速组合下，U型管的振动响应有相似的特点。图9所示为vout=10 m/s时的U型管振幅分布。从图9中可见，振幅由固支端向自由端增大，最大振幅出现在弯管段，且x方向振幅占主导。以振幅最大的弯管段及两段直管段中点（图1中A、B、C3点）作为特征点，分析U型管在内、外流共同作用下的振动特性。

图9 vout=10 m/s时U型管振幅分布

图10 所示为A点在不同内、外流速下各方向平均位移，图11 所示为A、B、C点在内流流速为0 时各点各方向平均位移。由图10、图11 可见，随着外流流速增加，x方向上平均位移向x轴正方向（阻力方向）增大，此规律与阻力变化规律一致；y方向上平均位移在0附近，且对外流变化并不敏感，此规律与升力变化规律一致；随着外流流速的增加，z方向上平均位移向z轴负方向增大，在数值上比x方向小两个数量级。

图10 A点各方向平均位移

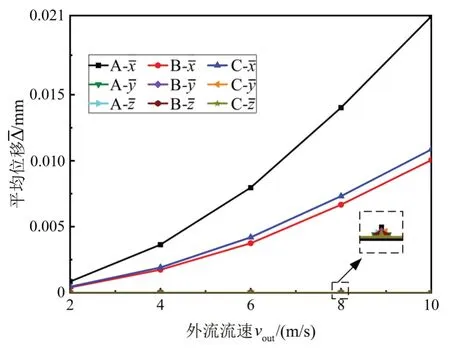
图11 vin=0时A、B、C 3点各方向平均位移

图12 所示为A、B、C3 点振动幅频特性，由于各点振动频率一致，本文以A点为例分析其变化规律。

图12 A、B、C 3点振动幅频特性

从图12可见，随外流流速升高，x方向位移峰峰值增大，此规律与阻力变化规律一致，振动频率均在阻力频率附近；y方向上vout=4 m/s时位移峰峰值最小，其后变化规律与升力变化规律一致，随流速升高，位移峰峰值增大，振动频率均在升力频率附近。vout=2 m/s 时升力频率（31.60 Hz）与U 型管一阶湿模态频率（29.27 Hz）接近，出现了共振现象，这是该外流流速下y方向位移峰峰值大于其他临近流速的原因；z方向上位移峰峰值变化与y方向一致，振动频率也与y方向振动频率一致。由图10 和图12(a)可知，U型管在x方向的变形占主导。

3.3 内流减振作用分析

图13所示为A、B、C3点x方向平均位移绝对值在不同内、外流速组合下的变化情况。从图13中可见，vin=2～4 m/s时，随外流流速升高，A、B、C3点x方向平均位移绝对值都出现了先减小、后增大的规律；而vin=6～8 m/s 时，随外流流速升高，A、B、C3点x方向平均位移绝对值都逐渐减小。这是由于x方向上内、外流体力作用方向不同，两者共同作用时，其对U 型管的影响会相互抵消。以vin=0 为参照线，内流对管道振动起抑制作用的有效区域如图13绿色阴影面积所示。

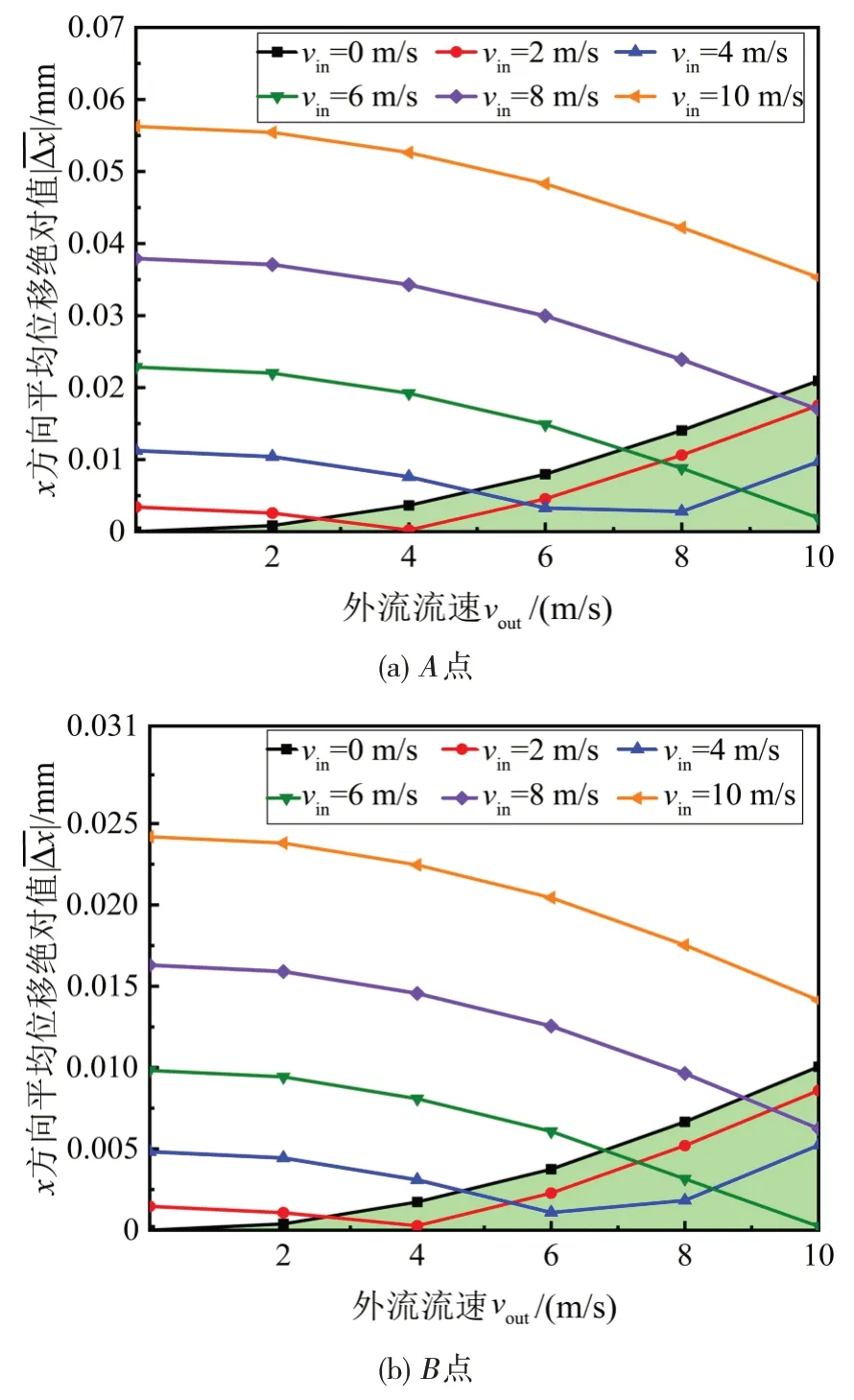
图14 所示为vout=8 m/s时A点x方向平均位移绝对值随内流流速的变化情况。由图14可见，随内流流速升高，A点x方向平均位移绝对值先减小后增大，即低流速的内流会削弱外流引起的管道振动，而过高流速的内流流速会导致x方向平均位移增大，又加剧了管道振动。

不同流速组合下A点的U型管减振效果如图15所示。从图15 中可见，在不同的外流流速下，随内流流速升高，减振效果均呈现先上升后下降的规律，存在一个最佳减振流速。vout=4 m/s 时，最佳减振内流流速为2 m/s，减振效果为94%；vout=6 m/s时，最佳减振内流流速为4 m/s，减振效果为59%；vout=8 m/s时，最佳减振内流流速为4 m/s，减振效果为80%；vout=10 m/s时，最佳减振内流流速为6 m/s，减振效果为91%。

4 结论

本文基于ANSYS Workbench 平台采用单向流固耦合方法，对外流流速为2～10 m/s 的空气及内流为2～10 m/s 的水作用下的单根U 型管内、外流场及振动特性进行了研究。主要结论如下：

1）单向流固耦合方法能够较好地实现对小变形下的管道流固耦合问题的计算。与双向流固耦合相比，可以提高计算效率。

2）系统主要激励来自外流，表现为涡脱激振力，与系统稳态响应的振动幅值及频率密切相关；内流则对平均位移及固有频率影响更为显著，其对U型管各阶固有频率的降低幅度约为11.9%。

3）内、外流体力的作用方向存在差异，在某些内、外流速组合下，x方向（阻力方向）出现了“抑制振动”的现象，即低流速的内流会使平均位移绝对值减小（例如vout=8 m/s，vin=2～6 m/s时）；内流流速过高时，则会导致平均位移增大，又加剧了管道振动（例如vout=8 m/s，vin=8～10 m/s时）。每一个外流流速都存在一个最佳减振内流流速，能够大幅降低U 型管的平均位移（例如vout=10 m/s，vin=6 m/s 时，减振91%）。

事实上，平均位移对管道与支撑结构间的碰撞、磨损问题的研究是至关重要的，因此，本文的结果对合理安排U 型管设备的内、外流速以达到减振效果有着积极的指导意义。