立足核心素养，提升关键能力，发展创新思维——以“直线与椭圆的位置关系中角的转化策略”的教学为例

北京市昌平区第一中学 刘克光

北京市昌平区教师进修学校 高丽娟

一、问题的提出

中国高考评价体系确立了“一核”“四层”“四翼”的整体框架，回答了“为什么考”“考什么”“怎么考”的问题，并指出：素质教育的突出特征之一是对创新性的强调。发散思维、逆向思维、批判性思维等思维品质是创新思维的重要特征。因此，培养学生的创新思维能力是我们教育的核心任务。在高三复习课中，笔者始终坚持把学生创新思维能力培养放在首位，针对学情创设问题情境，引导学生在探究中创新，在创新中继续探究，把创新思维能力的培养融入具体教学活动中，让问题解决内化在日常的数学教学过程中。下面以“直线与椭圆的位置关系中角的转化策略”单元设计为例说明。

二、通过单元整体教学，培养学生的创新精神

（一）深入研究学情，发现学生真问题

在高三第二轮复习中，笔者发现“角的关系”问题是当前学生解析几何复习中的突出弱项。

主要表现为四个方面：一是不能准确理解题意，理不清图形变化规律以及参数之间的关联；二是转化意识不强，不能准确完成几何条件代数化；三是字母运算能力太弱，达不到所建构模型的运算水平；四是解题思路单一，不能迅速建构简捷算法。因此，笔者设计了关于“角的转化策略”的教学单元，取得了良好的教学效果。

（二）单元教学目标

（1）通过实例探究，学会从几何与代数的双重视角，解决含有参数的直线与椭圆的位置关系中角的转化问题，能正确画图、识图，能合理转化与规范表述相应问题。

（2）通过对含有参数的直线与椭圆的位置关系中角的转化问题的探究过程，体验数形结合、转化与化归等数学思想的应用，提升逻辑思维能力、运算求解能力和创新能力等关键能力，发展直观想象、数学运算与逻辑推理素养。

（3）通过自主探究与小组交流的展示活动，创设开放性问题，提高从数学角度发现和提出问题的能力、分析和解决问题的能力，培养创新精神。

（三）单元教学设计

依照课标要求与学情分析，本单元设计为3课时。

第1课时：直线与椭圆的位置关系中的基本运算（夯实基础）

以2021年西城区期末、2022年石景山区一模中的解析几何解答题为母题，拓展探究弦长、垂直、定点等基本问题。培养化归与转化思想，提升逻辑推理与数学运算素养。

第2课时：直线与椭圆的位置关系中的角的转化策略（1）（本节课）

以高三一模解析几何解答题为母题，关联“两角的二倍关系”与“两角互余”问题，从建构线段长度、直线斜率、点的坐标、平面向量、三角函数等不同视角，拓展探究角的转化策略。提升逻辑推理、数学运算与直观想象素养，发展批判性思维与发散思维能力。

第3课时：直线与椭圆的位置关系中的角的转化策略（2）（思维拓展）

关联2015年高考理科、2019年西城区期末、2017年西城区理科试卷中的解析几何解答题，从建构线段长度、直线斜率、点的坐标、平面向量、三角函数等不同视角，拓展探究角的转化策略。提升直观想象、数学运算与逻辑推理素养，发展批判性思维与发散思维能力。

三、深研试题，优化课堂探究活动，提升关键能力

（一）培养数学阅读理解能力和信息整理能力

信息整理能力是指在对大量、无序的信息进行筛选、分类、归纳并形成新的意义的过程中所需要的多种能力，这是创新解决问题的重要能力。阅读理解能力是理解用汉字描述的数学定义、定理以及理解相应的符号与图形语言。数学思维以数和形为思维对象，以数学语言和符号为载体，以认识和发现数学规律为目标。图形语言着重展示图形中各元素之间相对位置关系和数量关系，需要考生读图、识图或者绘制图形，要能对图形进行加工、整理，抽象其中包含的解题关键信息。

（1）求椭圆C的方程；

（2）直线y＝kx＋m（km≠0）与椭圆C交于A、B两点，与y轴交于点P，线段AB的垂直平分线与AB交于点M，与y轴交于点N，O为坐标原点。如果∠MOP＝2∠MNP成立，求k的值。

学生的典型错误是不能恰当处理条件“∠MOP＝2∠MNP”，建立关于斜率k的方程，把几何问题恰当转化为代数问题，并完成相关计算。

教师引导学生认真读题、审题，画出有代表性的图形（如图1），认真观察图形，确定点M、N、P的坐标。教师提出审题三问。

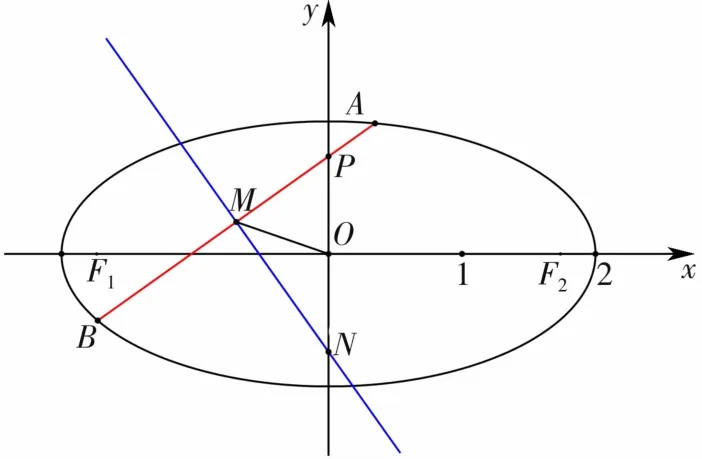
图1

1.看条件，可以得到什么？（理解参数变化规律，绘制动态图形，计算基本数据）

2.看结论，需要什么？（探究图形变化过程，厘清问题中数量关系与位置关系）

3.从条件到结论，如何搭建桥梁？（几何问题代数化：把两角的二倍关系转化为与直线斜率有关的方程）

（二）发展批判性思维能力与逆向思维能力

批判性思维能力是指面对各种问题情境，运用已有知识经验进行审慎思考、分析推理、评价重构等，这是学生解决问题的重要能力。在数学学科发现和提出问题，通过部分已知信息对结论进行猜测，通过逻辑推理验证猜想的探究过程就是批判性思维的具体体现。在高考中，对批判性思维考查体现在对于推理和论证的确认、分析、评价、展示过程中的逻辑推理。

高考数学解题，首先是正确，运用数学术语、符号、算式、推理步骤表达自己的思想。其次是规范，符合数学表达方式和要求，具有逻辑性和条理性。最后是简明，不迂回绕路、不拖泥带水。语言表达能力的基础是逻辑推理、运算求解能力、推理论证能力，只有清晰条理的思维，才能有规范流畅的表达。

问题2：（学生探究活动1：角的转化）结合图形分析，如何处理条件∠MOP＝2∠MNP？

教师引导学生，在学生自主探究与小组合作交流的基础上，从不同视角展开探究活动，通过学生展示过程，纠正学生在角的转化问题上的错误认知，优选算法，规范表达。

教师指导学生精细化阅读题目，再次提出审题三问。

1.两个角的位置关系。（所在的三角形，关联的直线等）

2.如何处理角的“二倍”关系？如何代数计算？如何构造“等角”？（相等的角的几何转化）

3.用代数方法如何表达角？（用直线斜率、线段长度、点的坐标等建构方程）

教学片段1：

学生1：因为MP⊥MN，所以以线段PN为直径的圆过点M，圆心为点O。

教师追问：圆心在哪里？（未必是点O）。

学生2：因为∠MOP＝2∠MNP，利用同弧所对圆周角与圆心角的关系可知，点M、N、P位于以O为圆心，｜OM｜为半径的圆周上。

教师追问：点P的位置能由条件∠MOP＝2∠MNP确定吗？

针对学生错误认知，教师提出下列问题，引导学生讨论，通过作图分析，辨明真伪。

（1）因为MP⊥MN，所以以线段NP为直径的圆过点M，所以｜OP｜＝｜OM｜＝｜ON｜。

（2）因为∠MOP＝2∠MNP，所以点M、N、P位于以O为圆心，｜OM｜为半径的圆周上，所以｜OP｜＝｜OM｜＝｜ON｜。

通过学生课堂探究与交流展示，完成了如下解题策略，并完成了相应规范解答（如表1）。

表1 关于条件∠MOP＝2∠MNP的不同转化视角

（三）发展发散思维与收敛思维能力

类比是一种重要的数学问题研究方法与学习方法，是一种常用的教学方法，也是一种发展数学创造思维的研究策略。教学的不同阶段，学生运用类比的能力各异。数学概念与运算的抽象性强，学生不容易理解和掌握，如果教师能通过新知识与已有知识之间的内在联系，运用恰当的方式，发现两者的异同点，对新旧知识的领悟与理解，将大有益处。

问题3：（学生探究活动2：落实转化、规范运算）

教师通过改编题设条件，引导学生思考题目条件之间的内在联系，弄清楚“等角”与“斜率”“线段长度”或“点的坐标”的内在关联，落实通法，优选算法。

教学片段2：

在自主探究与小组交流的基础上，教师引导学生从不同视角分析，展开探究活动。通过学生展示交流，纠正学生的认知错误，规范表达，引导学生选择适合自己的方法（设直线AB与x轴相交于点T，如图3）。

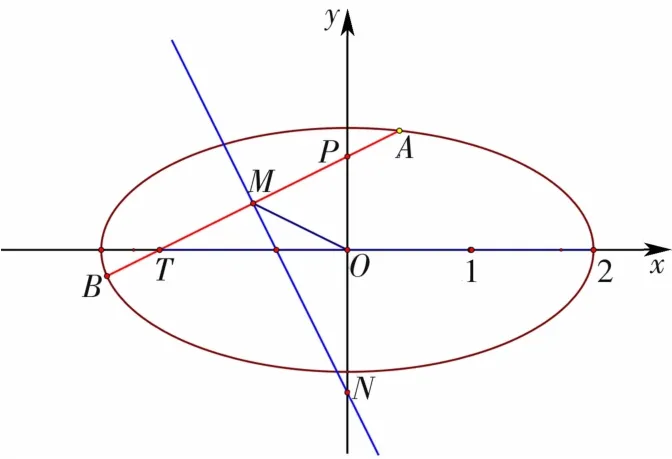
图3

学生3：因为∠MNP＝∠MTO，所以tan∠MNP＝tan∠MTO＝kAB。

教师追问：tan∠MNP＝kAB？（tan∠MNP＝｜kAB｜）

学生4：因为tan∠MNP·tan∠MOP＝1，所以｜kAB｜·｜kOM｜＝1。

教师追问：tan∠MOP＝｜kOM｜？直接表达不方便时，可以尝试换个角研究。

教师追问：如何用代数方法表示“∠MTO＝∠MOT”？

学生6：转化为线段长度，因为∠MTO＝∠MOT，所以 MT＝MO。

学生7：转化为直线斜率，因为∠MTO＝∠MOT，所以kAB＋kOM＝0。

学生8：转化为点的坐标，因为∠MTO＝∠MOT，所以xT＝2xM。

教师引导学生作图分析，小组讨论，纠正错误认知，得到正确结论。

在课堂小结中，教师引导学生归纳与类比，总结直线与椭圆位置关系中角的转化策略（如图4）。

图4

（四）创设开放性问题，发展创新思维

开放性试题由于条件、方法与结果的不确定性，所以呈现出条件开放、过程开放、结论开放等特点，且没有唯一固定答案，因此，在教育和评价中有特定的功能。开放性试题在考查学生思维的灵活性、创造性上更为突出。

笔者设计了如下问题，作为学生的课后思考题：

图5

图6 学生GGb软件作品

图7 学生几何画板作品

（1）如果∠MOP＝2∠MNP成立，求椭圆C的离心率e的取值范围；

（2）当a＝2时，认真观察本题图形，您还可以得到哪些结论？

第二问，学生得到了以下六个结论：

①kAB·kOM＝；

②△ABN是等腰三角形（NA＝NB）；

③四点M，S，O，P共圆（直径是PS）；

④四点T，M，O，N共圆（直径是TN）；

⑤TN⊥PS（先猜后证，看似正确，几何论证不易，解析法计算彰显魅力）；

⑥△TON与△POS相似，且∠OTN＝∠OPS。

作为课堂例题的拓展探究，本题解法灵活，运算的复杂度略有增加，引导学生体会条件的加强与减弱，理解数学概念的本质内涵，也即解题中适度的“进与退”策略，实现“化未知为已知，化繁为简，化难为易”，从而建构解题规范模式。其中，第二问开放性问题，有利于培养学生的发散思维与聚合思维，考查学生探究问题的敏感度、洞察力与独创性。

四、通过创新课程等方式，培养学生创新思维

“好的数学问题”是培养学生创新思维的重要载体，激发数学创新思维需要精心设计问题情境。为此，笔者开设了“高中数学创新思维引领”校本课程，通过对数学文化（数学史、数学美学）、数学建模、数学软件（几何画板、GeoGebra软件等）、对策论（最佳策略）、分形几何（经典曲线）等方面的小专题讲座，深化了学生对数学本质的理解，开阔了学生的视野。

在函数复习时，笔者设计了数学实践活动：请用不少于4个函数、曲线或者图形组合，借助GeoGebra、几何画板等数学软件自主设计创意Logo。要求上交源文件、成果图以及创意说明。

学生数学创新思维能力的培养是一个长期、渐进的过程，需要教师在教学的不同阶段，采用恰当的教学模式，通过建构开放性课堂，创新问题情境，倡导学以致用理念，优化课堂结构，激发学生的创新意识与创新精神，发掘学生潜能，从而最大限度地提升教学效率，真正培养学生的数学创新思维能力。