WNNM参数模型及迭代判断机制优化的遥感影像去噪

胡鹏程,卢献健,唐诗华,2,张炎,熊祖雄

(1.桂林理工大学 测绘地理信息学院,广西 桂林 541004;2.广西空间信息与测绘重点实验室,广西 桂林 541004;3.广西壮族自治区信息中心(广西壮族自治区大数据研究院),南宁 530028)

0 引言

图像在获取和传输的过程中会不可避免地受到各种因素的干扰,导致图像的质量降低,无法有效地从图像中获取所需的信息[1]。高质量的光学遥感影像对于农业和林业监测、城市规划、军事侦察等领域具有广泛的应用场景,因此通过图像降噪能提高图像质量,并为图像的后续步骤提供预处理[2]。

现有图像降噪算法中效果较好的是基于非局部自相似性(nonlocal self-similarity,NSS)的相关算法,利用图像在一定区域内的相似性进行降噪,能有效地保留图像的纹理细节,其中以非局部均值(non-local means,NLM)[3]和三维块匹配 (3D block matching,BM3D) 算法[4]为代表。另一种利用图像的自相似性进行图像降噪的方式是通过低秩矩阵恢复(low-rank matrix recovery,LRMR)[5]。而Fazel[6]提出核范数最小化(nuclear norm minimization,NNM)算法,构建低秩聚类去噪模型,再通过奇异值[7]进行软阈值[8]收缩得到去噪图像,该算法问题在于使用同一个奇异值导致图像细节过于平滑而模糊。Gu等[9]在此基础上提出加权核范数最小化(weighted nuclear norm minimization,WNNM)算法,将不同的权值赋予奇异值,提高降噪性能。但WNNM算法依旧存在低秩信息无法高效地与噪声进行分离和经验参数过多的问题,徐望明等[10]提出一种自适应加权低秩矩阵恢复的算法,通过对于奇异值和软阈值进行自适应加权,获得更好的去噪效果。

针对WNNM算法经验参数过多导致去噪性能下降的问题,本文提出一种基于加权核范数最小化参数模型优化的遥感影像去噪方法。利用GA算法[11]优化 WNNM算法中的参数模型(非局部补丁搜索窗口、迭代步数、迭代之间的变换参数),并在算法迭代计算中加入判断机制,当迭代得到最优解之后跳出迭代循环,减少迭代时间,提高算法效率。在图像仿真实验和遥感影像实验之后,通过主观视觉评价[12]和客观指标评价均得到优于原WNNM算法和其他经典算法的结果。

1 基础算法

1.1 WNNM算法

WNNM算法通过欧氏距离衡量块与块之间的相似度,划分出非局部相似块组矩阵,再利用无噪声的相似块矩进行低秩矩阵复原得到降噪图像[13]。

1.2 GA算法

GA算法是基于优胜劣淘遗传机制的随机化搜索方法,其采用随机的方式进行全局寻优,能自动获取和自适应调整搜索空间,具有鲁棒性强、适用于并行计算等特点[14]。其主要分为3步。

1)选择。首先初始化种群,以适应度作为选择下一代个体的准则。通过设定目标函数,计算上一代种群的目标函数,当适应度越大时,选中的概率越大,因此基于轮盘赌选择适应度大的染色体进行遗传,选择目标函数解最优的个体成为繁衍下一代的个体。

2)交叉。在第一步被选为用于繁殖下一代的个体群中,随机选择两个不同的个体,然后以设定的交叉概率,在两个个体的同一位置进行交换,其中交叉概率一般设定为0.25～0.8,其目的在于进行信息交换并产生新的基因个体,其本质是增加种群多样性。

3)变异。通过变异概率对部分位置进行变异,因变异概率较小,一般设定为0.01～0.2。其目的为保证算法在进化过程中不会出现同一群体,即个体相同时交叉无法形成新个体,通过变异可以形成新个体。当迭代到阈值或收敛值时,输出最优个体。因此,在基于GA算法高并行计算能力的特点下,快速寻优重建WNNM算法参数模型。

2 优化算法

2.1 算法原理

WNNM算法中具有一个参数模型,其中包括噪声图像方差、非局部补丁收缩窗口、迭代变换参数、权重、内部重块匹配间隔数、块大小、初始非局部补丁数量、迭代次数、噪音估计参数等。参数模型中的大部分参数是通过经验值进行选择,在不同的噪声强度下无法自适应地更改,原模型当中,部分参数会随着噪声的增加而进行改变,但依旧具有改进空间。

本文经过大量的实验之后,选择对于非局部补丁收缩窗口、迭代变换参数、迭代次数进行改进,其中对于每个迭代步骤之间的参数delta使用GA算法进行优化,以PSNR作为目标适应度函数,对于收缩窗口和迭代次数通过实验之后进行改进。同时,在实验过程中发现使用WNNM进行遥感影像的去噪时,在PSNR值达到最优之后不会自动终止,因为原迭代次数是通过经验值设定,导致降噪效果反而降低,因此最后加入判断机制,当迭代到最优解之后,返回最优估计图像。

2.2 算法流程

1)优化参数。通过GA算法优化delta参数,设定种群和个体为4,迭代次数为5,交叉概率为0.8,变异概率为0.1。因为原delta参数为0.1,因此设定寻优界限为0.05～0.2,最后将得到的最优解作为参数输入到参数模型中。

delta参数的寻优过程如图1所示,可以发现随着高斯噪声的强度增加,delta的值会发生改变。当标准差σ为5、10时,参数值最优值为0.11;标准差σ为15、20时,参数值最优值为0.12;标准差σ为25时,参数值最优值为0.13;标准差σ为30时,参数值最优值为0.14。因此,经过实验发现delta参数值随噪声强度增加而变大。

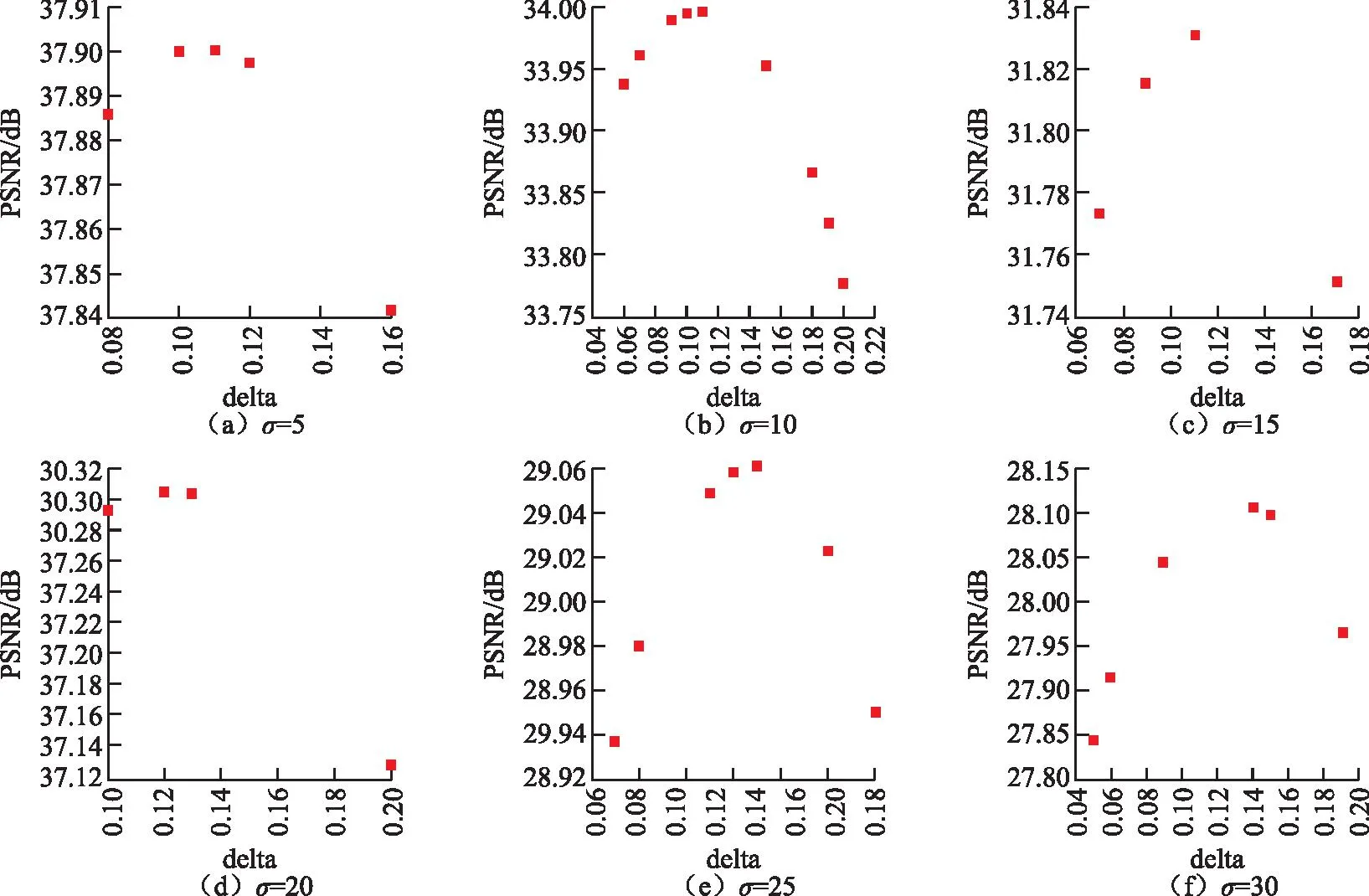
图1 GA优化delta参数

而搜索窗口大小经过多次实验发现,相较于原大小为30,修改为40后图像处理效果更优。而迭代步数经过实验发现,当高斯白噪声标准差σ小于20时,修改为9步效果更优。最后将修改之后的参数重新输入到参数模型中进行WNNM降噪。

2)WNNM降噪。通过将优化后的参数重新构建参数模型后,进入迭代循环,估计的噪声方差归一化F范数的保真项,在保护信号的同时去除噪声。再进行迭代正则化[15],得到图像的非局部相似块组,通过估计权重进行奇异值分解,之后进行重构估计图像,计算估计图像的PSNR值,并构造一个结构体,将此次循环下的PSNR和估计图像赋值其中。再对结构体中的PSNR进行判断最优值,如果此次循环下的PSNR小于结构体中最大PSNR值,则说明上次迭代已达到最优值,打断迭代循环,并将上次估计图像作为参数返回。流程图如图2所示。

图2 GA-WNNM去噪流程

3 实验与质量评价

3.1 灰度图像仿真实验

通过MATLAB R2018b软件进行灰度图像仿真实验,以验证本文算法的有效性。选用经典图像处理数据集Set12中的灰度图像进行仿真,并与BM3D、NCSR[16]、WNNM算法进行对比,利用PSNR和SSIM进行指标评价分析[17],其中PSNR值越大效果越优异,SSIM值越接近1效果越好[18]。本实验分别对256像素×256像素的灰度图像Starfish添加均值为0,标准差σ为5、10、15、20、25、30的高斯噪声,然后将加噪之后的图像集作为噪声图像测试集。当σ为30时,去噪对比效果如图3所示,评价指标如表1所示。

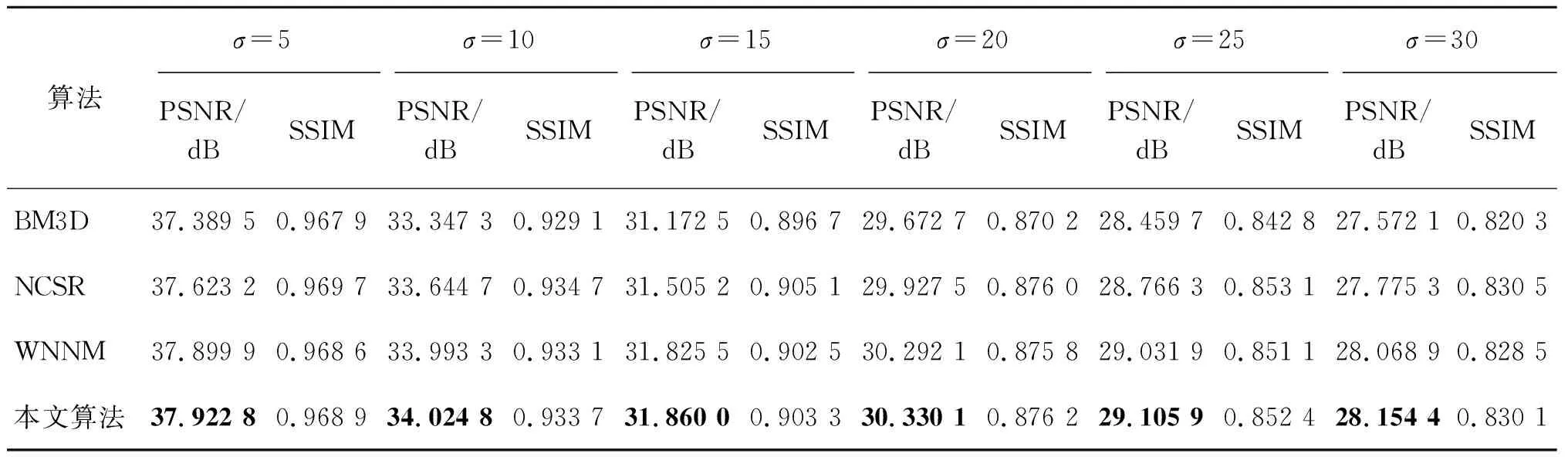
表1 Starfish去噪质量评价指标

图3 Starfish去噪对比图

从表1可以发现,加黑数据为PSNR最高值,而本文算法相较于BM3D、NCSR、WNNM在PSNR值上具有最优的效果。与WNNM算法相比,本文算法从低噪声强度到高噪声强度都具有更好的效果,同时随着噪声强度的增加,提升的效果更大。从SSIM方面来说,NCSR算法具有最好的效果,原因在于利用图像的自相似性获得稀疏编码系数,通过非局部集中稀疏表示模型来重建输入图像,因此在结构相似度上具有最好的效果。但是相对而言,本文算法是其余3种算法中SSIM最优的算法,在σ为20时,甚至达到4种算法中的最优值。同时,随着噪声强度的增加,本文算法相较于原WNNM算法,其PSNR和SSIM值均逐步提高。

从图3可以验证上述数据结论。图3(c)是BM3D去噪图像,其红框部分过于平滑,导致众多的纹理细节被平滑掉,保留的细节信息最少,与表1中的结论相同,是降噪结果最差的算法。图3(d)是NCSR去噪图像,相较于图3(c),其红框部分保留更多的纹理细节,但是去噪效果不如图3(e)和图3(f)。图3(f)是本文算法降噪图像,与WNNM算法降噪的图3(e)相比,在总体上,二者的视觉效果差距不是很大,但是从图3(f)中的其余红框处可以发现,改进后的本文算法在具有优异降噪能力的同时具有更优秀的边缘纹理细节保留能力。

3.2 Landsat 8遥感影像实验

本实验选择Landsat 8在2018年10月8日拍摄的一景数据,选择其中空间分辨率为30 m的band1 coastal影像,通过桂林市雁山区矢量数据裁剪,得到雁山区影像数据,为提高运行速率,截取349像素×349像素的遥感影像进行实验,以验证本文算法的普适性和有效性。本节实验与灰度仿真实验方法相同,当σ为30时,去噪对比效果如图4所示,评价指标如表2所示。

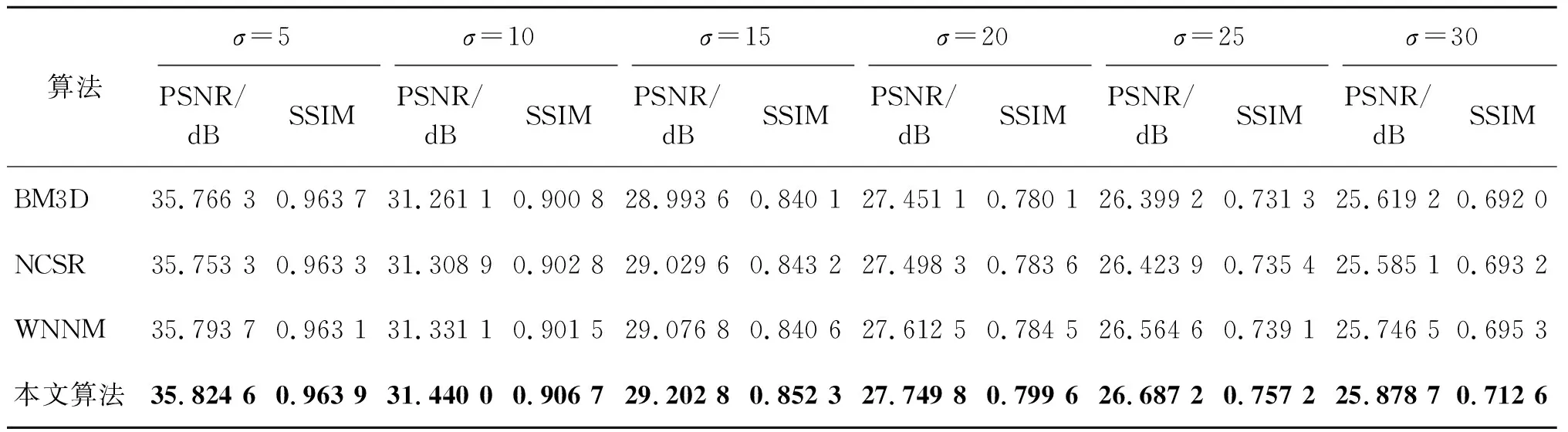
表2 Landsat 8遥感影像去噪质量评价指标

图4 Landsat 8遥感影像去噪对比图

充分观察影像效果,对图4红框区域进行放大处理,局部放大对比图如图5所示。

图5 局部放大对比图

从图4(c)和图5(c) 发现,BM3D算法会对影像过度平滑,造成影像的纹理细节丢失,且图5(c)中的伪影现象严重[19],可见其去噪能力较低。从图4(d)和图5(d) 发现,NCSR算法具有更好的去噪效果,能够保留一定的纹理细节,但是图5(d)红框位置的伪影现象非常严重,且部分纹理模糊。从图4(e)和图5(e)发现,WNNM算法的细节保留能力优于NCSR算法,同时比较图5(e)和图5(d)同一红框以及蓝框位置,发现图5(e)的伪影少于图5(d)。

图4(f)是本文算法影像去噪图,从红框区域可以发现去噪效果最好,河流区域的边缘保留更为充分,蓝框区域可以发现纹理信息更丰富。图5(f)可以发现影像经放大之后,对比信息更为明显,其红框区域保留信息与原图更为接近。同时,在蓝框区域梯度变化较少地区,对比算法对纹理信息过平滑,导致影像缺少细节结构,而本文算法通过特征提取窗口的优化,获取更为丰富的纹理细节。

表2可以与图4和图5相验证。从表2中可以发现加黑数据为最优解,本文提出算法在所有噪声程度上,PSNR和SSIM值均为最优,这与灰度图像实验具有一定区别。表1中本文算法PSNR同样为最优解,在SSIM值上虽然优于原WNNM算法,但是弱于NCSR算法。

从表2可以看到,PSNR值依然为所有对比算法中的最优,SSIM值成功优于NCSR,成为所有对比算法中的最优值。这是因为NCSR是基于非局部自相似性进行稀疏表示重建图像,在图像复杂程度较低时拥有一定优势,但是遥感影像结构复杂,因此效果不佳。而本文算法在优化非局部补丁搜索窗口参数之后,对于影像细节特征提取更为丰富,因此在保留影像结构方面具有更好的表现。

同时,与原WNNM算法进行比较发现,PSNR值稳定提升约0.13 dB,SSIM值随着噪声强度增加,提升效果更明显,提升约1.5%。并且从表中能够发现,其余对比算法SSIM值整体处于均等位置,区别于灰度图像,而本文算法则是明显超出各对比算法。

从表3可以发现,本文算法在大部分噪声情况下计算时间方面优于WNNM算法,通过研究发现由于遥感影像的细节丰富,降噪的难度会随着噪声强度的增加而增大且降噪的质量下降快速,而原WNNM算法根据经验固定迭代次数,适用于图像降噪,但是在遥感影像降噪过程中,会出现迭代到中间步数就达到最优情况,如果继续迭代,反而会降低影像质量。因此,加入判断机制,创建结构体存储每次迭代的PSNR及估计图像,当一次迭代完成后进行判断是否最优,如果此次迭代的PSNR小于结构体中PSNR,则说明图像质量开始下降,将上一次存储的估计图像返回,在提高图像质量的同时节省程序运行时间,提高计算效率。

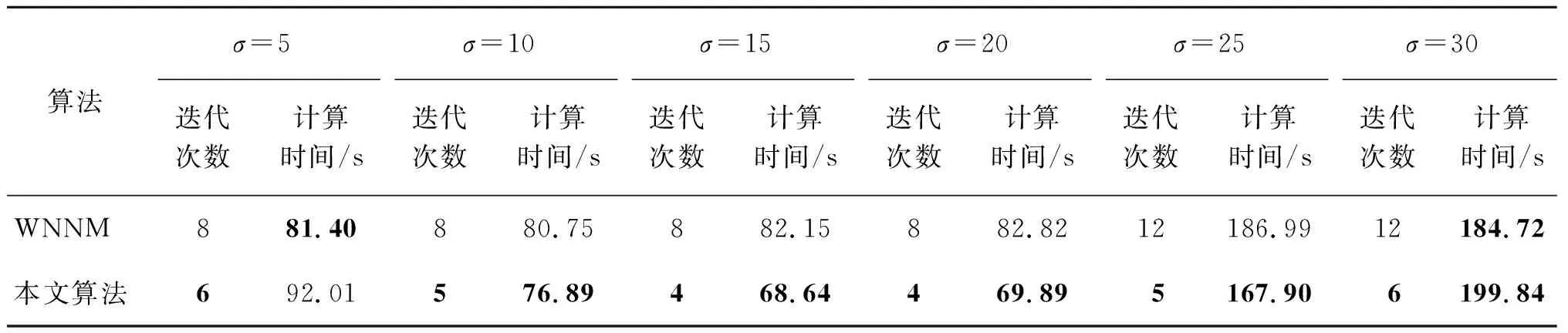
表3 运行迭代次数与计算时间

同时从表3发现,本文算法在迭代次数上均少于WNNM算法。在大部分噪声情况下,计算时间少于WNNM,但在少部分情况下计算时间高于WNNM,原因是本文算法增大非局部搜索窗口,在增强图像特征的提取能力的同时增加运行计算量。表3中记录迭代次数为最优解次数,在实际运行中,迭代次数需增加1次,因为此次运行结果与之前最优解进行判断,当小于最优解之后跳出迭代,得到上一次结果为最终最优解。

3.3 GF-1遥感影像实验

为验证本文算法在高分辨率影像数据中依然具有可行性,选择高分一号(GF-1)卫星在2015年4月19日拍摄的一景桂林市影像数据进行实验。首先,选择其中空间分辨率为2 m的全色波段影像,通过全色辐射定标和正射校正进行图像预处理。然后,截取1 547像素×1 116像素的影像进行实验,提高运行速率的同时影像细节更丰富。本实验与灰度仿真和Landsat 8实验方法相同,当σ为30时,去噪对比效果如图6所示,评价指标如表4所示。

表4 GF-1遥感影像去噪质量评价指标

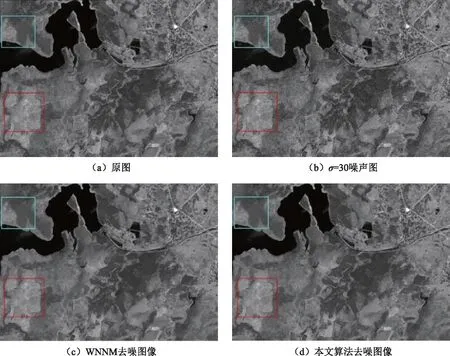
图6 GF-1遥感影像去噪对比图

从灰度实验和Landsat 8实验可知,WNNM算法以及本文算法具有更好的效果,因此本节实验主要比较本文算法与WNNM算法之间的效果差异。因为本节实验影像分辨率较高,计算开销大,因此将本文算法中的非局部搜索窗口调整为35。从图6看到,红框区域本文算法的影像明亮度信息与原图之间的相似度最为接近,同时结合蓝框区域,本文算法的纹理细节保留更为充分,与原图的边缘纹理结构更为相似,而WNNM算法对于影像平滑程度更高,损失掉部分细节信息。因此,能够说明本文算法的有效性。

表4与图6可以显示出本文算法在PSNR以及SSIM值上均优于WNNM算法,并且PSNR和SSIM值随噪声强度增加而二者之间的差距更大,说明本文算法对于高强度噪声适应度更强,性能更优异。

表5与表3相比,变化较大。从迭代次数上来说,依然保持相同规律,少于WNNM算法的迭代次数,说明判断机制对于其余遥感影像依然生效。从计算时间上来说,所有噪声情况下,本文算法时间均少于WNNM算法,体现算法的高效性。但是随着影像分辨率的增大,整体计算时间也随之增加,在后续研究中还需优化算法的时间复杂度。综合而言,在大部分噪声情况下,本文算法具有更少的迭代次数以及更短的计算时间。因此,本文算法在去噪的有效性、普适性、计算效率均最优。

表5 运行迭代次数与计算时间

4 结束语

针对加权核范数最小化算法经验参数多、无法有效自适应复杂环境下的遥感影像高斯白噪声去除问题,本文提出一种利用遗传算法优化加权核范数最小化算法中的迭代参数,改进非局部补丁搜索窗口、迭代步数并在算法迭代计算中加入判断机制的遥感影像去噪方法。经过灰度仿真实验和Landsta 8、GF-1遥感影像去噪实验,与BM3D、NCSR、WNNM算法通过PSNR和SSIM进行对比分析,本文算法具有最优的PSNR和SSIM评价指标。在遥感影像实验中,本文算法相较于WNNM算法,PSNR和SSIM的差值均随噪声强度增加而增加。

因此,本文算法在有效去除噪声、保留纹理细节信息的同时降低伪影影响,提高运行效率。下一步的研究方向在于如何改进本文算法,提高单次迭代的计算效率,并且如何更有效地去除伪影的影响也是研究的重点。