基于地平拟合改进的激光点云滤波算法

代震,何荣,白伟森

(河南理工大学 测绘与国土信息工程学院,河南 焦作 454000)

0 引言

随着实景三维中国建设的需求,对数字高程模型(digital elevation model,DEM)的精度要求越来越高,与以往为灾害监测、地形绘图等方向的支撑不同,精细DEM更能参与到智慧城市的建设中,关系到城市级实景三维模型的质量。其中三维激光的广泛应用,使得获取地面目标的精确点云变得更加容易,点云处理技术已成为测绘领域的一个关键研究方向[1-3]。

现有的点云滤波方法一般分为3类。一是基于坡度的方法[4],该方法原理是以任意点构建圆锥体,根据点云数据中地面坡度的大小分离地面点和非地面点。原理相对简单,坡度滤波核运算效率较高,但阈值设置困难,大多是依靠经验量,同时算法在地形复杂的区域表现不佳。二是基于表面的方法,代表算法有渐进加密三角网滤波算法(progressive tin densification,PTD)、布料模拟滤波算法(cloth simulation filter,CSF)等[5-9]。PTD算法原理是随机选取局部区域最低点作为种子点,然后根据上述种子点构建稀疏三角网模型,通过判断点云数据是否满足距离和角度阈值来分离地面点和非地面点。该算法能够较好地保留地形陡峭区域的地面点,是目前较稳健的算法之一。陈琳等[10]在2014年运用高程统计的方法,进一步升级基于先验经验的PTD滤波算法,提高了滤波效率。凌晓春[11]在2020年引入薄板样条曲线插值法,通过TPS中的弯曲能力增长值对PTD算法进行改进,减少了滤波误差。CSF算法原理是想象一个可以改变刚性系数的布料,缓缓下沉到倒置的地形上,以此得到地面点。该算法参数较少且易于设置,在平面地区具有极佳的滤波效果,但无法应对高程变化剧烈的复杂地形。石壮等[12]在2022年通过虚拟格网划分不同地形,分别采用对应的参数进行滤波,比单一CSF滤波更适用于混合地形。王佳雯等[13]提出一种基于地面点归一化的滤波改进方法,显著提高滤波精度。三是基于形态学的方法。该方法通常采用数学应用中的膨胀和腐蚀运算,以固定的窗口分离地面点和非地面点。Zhang等[14]在2003年提出了一种经典的渐进式形态学滤波算法,该算法关系窗口尺寸、地形坡度、高差阈值等参数,由于阈值的设置较为困难,使其一方面难以去除近地面点,另一方面容易导致陡峭区域过度滤波。隋立春等[15]在数学形态学“开”算子的基础上,首次提出“带宽”的概念,通过增加该参数以提高最终滤波效果。苗启广等[16]在经典形态学算法的基础上,针对阈值设置问题,通过建立分块区域预测地形坡度,可以根据区域地形起伏情况自适应地调整阈值,得到最终结果。Pingel等[17]在前人研究的基础上提出简单形态学滤波算法(simple morphological filter,SMRF),利用输入的最大滤波窗口尺寸、地面高程、地形坡度3个参数生成临时地表,分类原始激光点云,算法更适用于城市地形,在非城市区域滤波误差较大。

因此,针对上述SMRF算法在非城市区域滤波效果的不佳表现,以及地面平面拟合算法在平缓地形的滤波优势,本文提出了一种基于地面平面拟合和简单形态学滤波结合的点云滤波算法。算法能够在抑制Ⅰ类误差增大的前提下进一步剔除近地面点,大幅降低Ⅱ类误差,提高生成的DEM质量。

1 算法原理

从宏观层面上来看,多数算法无法应对大尺寸、多变化的地形地貌,尤其是在面对高程变化剧烈的陡坡区域,滤波误差远远超出预料;反而对于较为精细的地物划分,具有较好的滤波效果。基于此类思想,在考虑到点云密度、曲率等多方面因素的影响权重,将剧烈变化的高程压缩到较小范围的轻微起伏也变成最有效策略。

本文具体算法流程如图1所示,提出的滤波算法包括4个改进步骤:简单形态学粗滤波、DEM辅助的高程归一化、地面平面拟合算法和空间向量后处理。

1.1 简单形态学粗滤波

渐进式形态学滤波算法是直接对原始点云进行处理,分离出的非地面点主要依靠形态学开运算的独立筛选,处理过程不仅耗时耗力且容易造成误判。而简单形态学算法使用多尺寸窗口构建栅格,以此生成临时地形表面,通过多次迭代使表面吻合实际地形,最后统一进行地面点与非地面点的划分。

算法首先创建一个名为lastsurface的ZI副本。保留每个像元内所有激光雷达点的最低高程,取代像元内剩余点云的高程,判断栅格单元内点云数量为0时使用图像修复技术插值。构建圆盘形结构,对lastsurface进行数学形态学开运算,如果原数据高程与开运算结果高程之差大于设定参数(机载激光数据默认为0.3),把该点当做空单元,使用图像修复技术进行插值,小于设定值,就把该点看做地面单元。激光数据需要不断迭代,迭代步长为一个单元,需要提前设置好最大尺寸。处理后创建临时DEM,保留ZI中被确定为地面的单元,然后根据原始点与临时DEM间的高差进行分类。

1.2 DEM辅助的高程归一化

在实际实验中,根据最大最小点云坐标的高程归一化结果误差较大,容易受到植被和建筑物的影响。因此采用SMRF滤波生成的粗DEM进行高程归一化,归一化原理如图2所示。

首先采用不规则三角网生成粗DEM,然后统计原始点云坐标,构建格网映像,通过待处理点云坐标投影格网,找到对应的DEM拟合高程数据,与待处理点云的原始高程作差,得到新的归一化值。同时,保留激光脚点的原始高程值,便于处理后反归一化。

1.3 地面平面拟合算法

高程归一化后的点云趋近于平缓地形,这些区域的地形可以看作连续分布的曲面,在相对较小的区域内,该曲面可以近似为等效平面。本文在地面平面拟合的基础上,加入渐进移动窗口和格网的改进步骤,同时以每个格网内的最低点作为数据集拟合平面模型,以此形成多个平面切片。算法步骤如下。

步骤1:建立索引机制,以快速查询每个点所在的网格和每个网格包含的点。点与网格间的索引关系的计算如式(1)所示。

(1)

式中:(X,Y)为网格号;(x,y)为点云的平面坐标;(xmin,ymin)为整个数据集的最小平面坐标;m为网格单元,即移动窗口大小;INT表示对计算结果向下取整。

步骤2:种子点选取。在每个格网内,索引最低点构建种子数据集S:si{i=1,2,…,n}(n≥3),定义平面为

ax+by+cz+d=0

(2)

假设w=(abc)T,x=(xyz)T,式(2)简化为式(3)。

-wTx=d

(3)

步骤3:拟合平面模型。通过初始种子点集S构建协方差矩阵C∈R3×3,如式(4)、式(5)所示。

(4)

Cx=λx

(5)

(6)

单一阈值的设定具有局限性,窗口变换的同时渐进缩小地面点提取阈值D0,滤除与当前模型距离较大的点。通过大量实验,设置D0初始值为5、步长为0.8时,提取效果最佳。平面距离D与阈值D0比较,若D≤D0,将P点作为地面点合并到此面集;若D≥D0,则作为非地面点滤除,重复数次后得到较为精确的平面点集。

1.4 空间向量后处理

在实际应用中,平面模型的构建容易受到其他地物的影响。为了提高地平面拟合的精度,利用区域空间向量投影,验证所拟合地平面的准确性,避免将一些异常平面(如建筑顶面、立面等)分割成地面。首先,统计各面片集合点云数量,从多到少依次排列,以点云数量最多的面集作为标准平面,设置标准法向量q;然后,对后续拟合出的地平面集合进行判断,空间向量二面角公式为式(7)。

(7)

式中:p为待测平面集合的法向量。

由此计算出二面角,通过与阈值比较,若小于阈值,则与标准平面合并。针对二面角阈值的设置问题,太大容易造成多个平面过度合并;设置太小容易造成地平面过度分割。提出一种根据各面片集合点云密度判断的解决方法,待测面片集合的点云密度越接近标准平面点云密度,越可能是真实地平面,公式为式(8)。

(8)

式中:ρ为标准平面点云密度;ρi为待测面片点云密度;α0为二面角阈值初值;αi为待测平面二面角确定阈值。

2 实验与分析

2.1 数据来源

实验数据分为两类。第一类实验数据采用飞马D-LiDAR2000系统于2021年4月14日获取,采集地点位于河南理工大学南校区,激光数据如图3所示,点云密度为7.49/m2,同时采集实验区域GPS点位进行算法验证。第二类实验所用数据来自国际摄影测量与遥感协会(ISPRS)官方网站发布的标准点云数据,数据采集地点位于 Vaihingen/Enz测试场和Stuttgart市中心,选取8组具有代表性的测试数据进行实验,如表1所示。两组实验数据包含建筑物、公路、植被、陡坡等不同地物特征,基本对应常见地形,数据集已手动分离出地面点和非地面点。

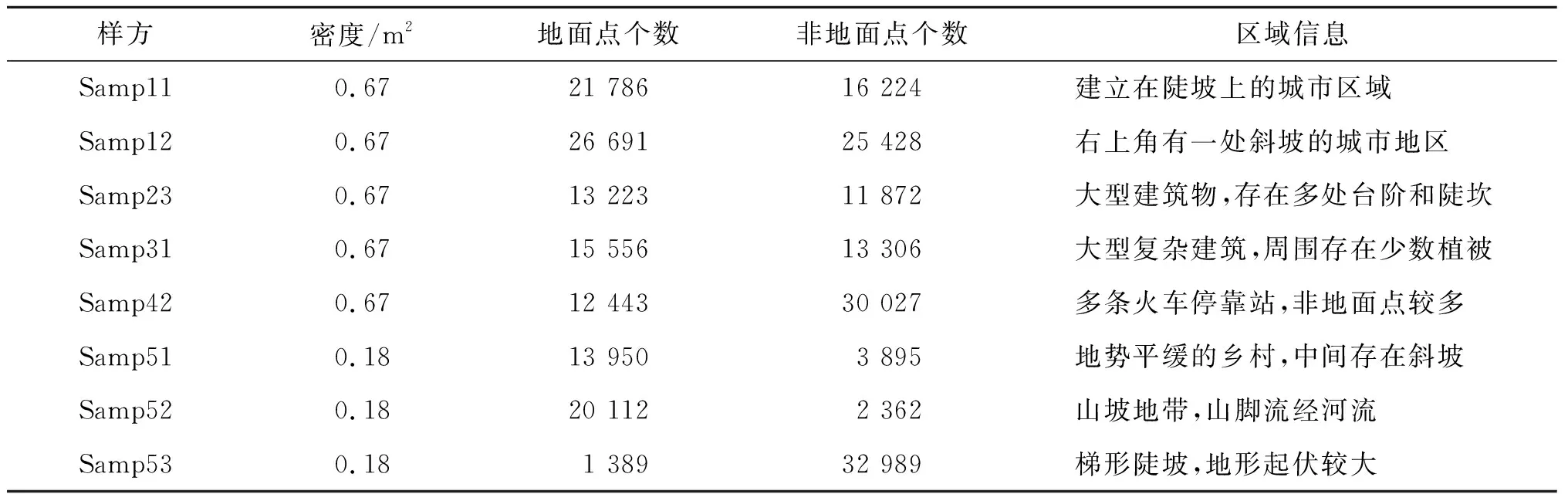
表1 研究区域点云基本情况

图3 河南理工大学南校区

2.2 理工校区DEM精度评价

本文采用不规则三角网方法处理滤波后的实验数据,以SMRF算法和改进算法提取的地面点分别生成DEM模型,由两种算法对应的DEM精度反映二者的滤波精度。已知41个GPS地面检查点的三维坐标,将其视为真实地面高程,从生成的DEM模型中提取相同点位的拟合高程值。取拟合高程值与真实高程值差值的中误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)作为滤波精度的判别依据,并分别与实际地形进行拟合。

由图4中残差分布可知,两种滤波算法滤波后DEM的残差分布趋势大体相似,但是SMRF算法对应的DEM的残差比改进算法波动振幅大,改进算法的波动更为平缓,产生的误差更小。

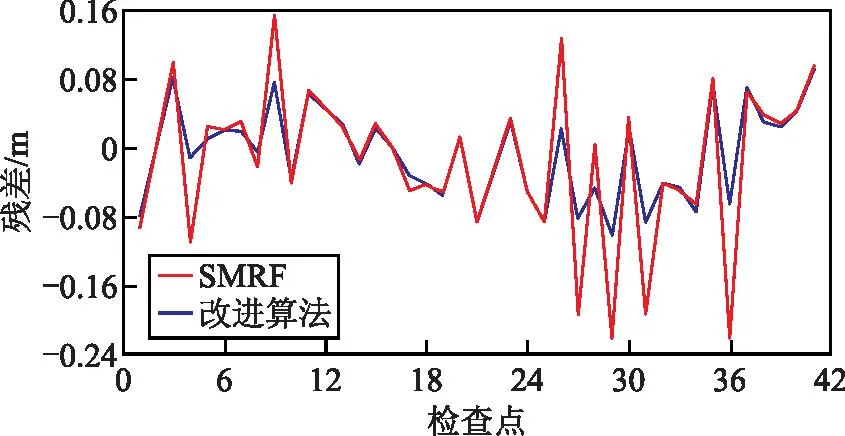
图4 残差分布

由表2可知,与SMRF算法相比,改进算法的中误差降低了3.3 cm,平均绝对误差降低了2.0 cm,证明改进算法能够有效地降低点云误差。将两种算法分别与实际地形线性拟合,如图5、图6所示,改进算法生成的DEM模型与实际地形的拟合效果更好、相关度更强,更加逼近于真实地形。

表2 DEM指标统计 m

图5 SMRF算法与实际地形线性拟合

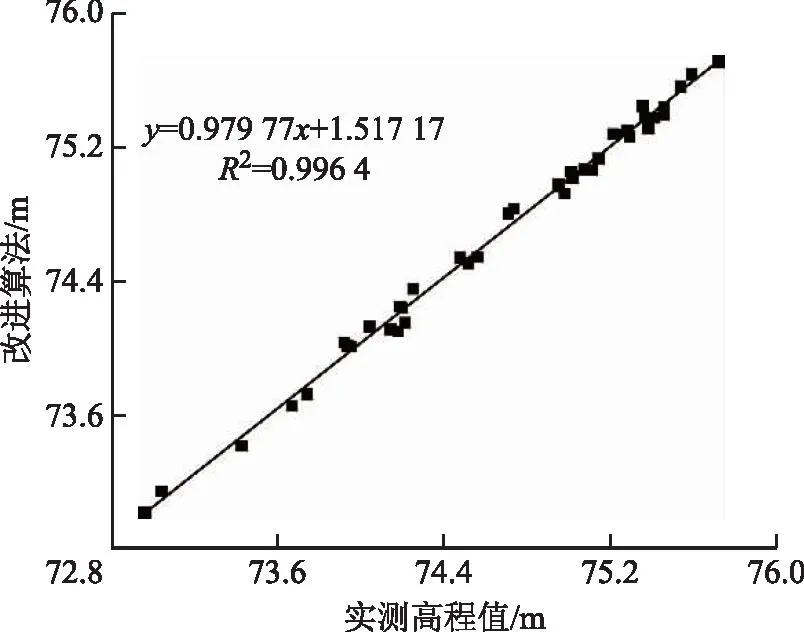
图6 改进算法与实际地形线性拟合

2.3 国际标准数据评价

以国际标准数据进行多种算法比较,本文采用2003年美国国际摄影与遥感协会提出由混淆矩阵推导的一种交叉表评价体系,如表3所示。其中,Ⅰ类误差(TⅠ)是指地面点中被错误地划分到非地考虑到CSF滤波算法误差较为典型,分别使用CSF算法、SMRF算法和本文算法对8组数据进行实验并比较,得到的Ⅰ类误差、Ⅱ类误差和总误差结果如表4所示。根据表4可以看出,本文算法的Ⅰ类误差、Ⅱ类误差和总误差分别为2.54%、7.47%和3.06%,均小于另两种算法。为了更好地验证实验效果,这里展示了地形显著、效果明显的Samp11、Samp23、Samp52滤波结果,并进行对比分析。

表4 各研究区滤波结果统计 %

面点的数量占地面点总数的百分比,Ⅱ类误差(TⅡ)表示非地面点中被错误地划分到地面点的数量占非地面点总数的百分比,总误差(TⅢ)是分类结果与参考数据不一致的概率。

进一步分析,本文算法在各个实验区的Ⅰ类误差均小于8.1%,表明该算法在处理陡坡、大型建筑物、植被覆盖和数据间断地形环境时容易得到地面点,同时能够保留更多的地形细节;处理实验区Samp51、Samp52时Ⅱ类误差较大,这说明本文算法在处理低矮植被和河流河岸区域时容易将非地面点判别为地面点,而Ⅱ类误差通常较容易通过人工剔除。

Samp11数据是建立在斜坡上的城市区域。如图7(a)的圆圈标注所示,在斜坡坡度变化最大区域和较高建筑区域,CSF算法将地面点云当成非地面点剔除,出现点云空洞较多,原因是密集城区的集聚,布料硬度参数和迭代次数都设置的较小,对于斜坡区域来说,地形起伏和建筑落差较大,地面点容易被当作非地面点剔除。如图7(b)的圆圈标注所示,SMRF算法将一些低矮建筑物和植被区域附近的地面点错误剔除,降低滤波精度,原因在于低矮地物过于贴合地面,干扰滤波过程。而本文方法在相应坡度较大的区域,仍保留地形细节。

图7 不同算法对Samp11的滤波效果对比

Samp23数据是典型的大型复杂建筑区。如图8(a)所示,右上角圆圈标注是明显的低矮建筑物,CSF算法错误地把非地面点判断成地面点;而左下角圆圈标注,由于建筑台阶依托的地势较低,远低于正常路面,形成坡度变化较大的地形条件,CSF算法滤波有明显的点云空洞出现。如图8(b)的圆圈标注所示,SMRF算法错误地将地面点判断成非地面点,该区域地势略高于路面。对比结果显示本文算法在大型建筑区具有很好的滤波效果,对略低于或高于正常地面的建筑台阶也能很好保留,并作为地形地物特征。

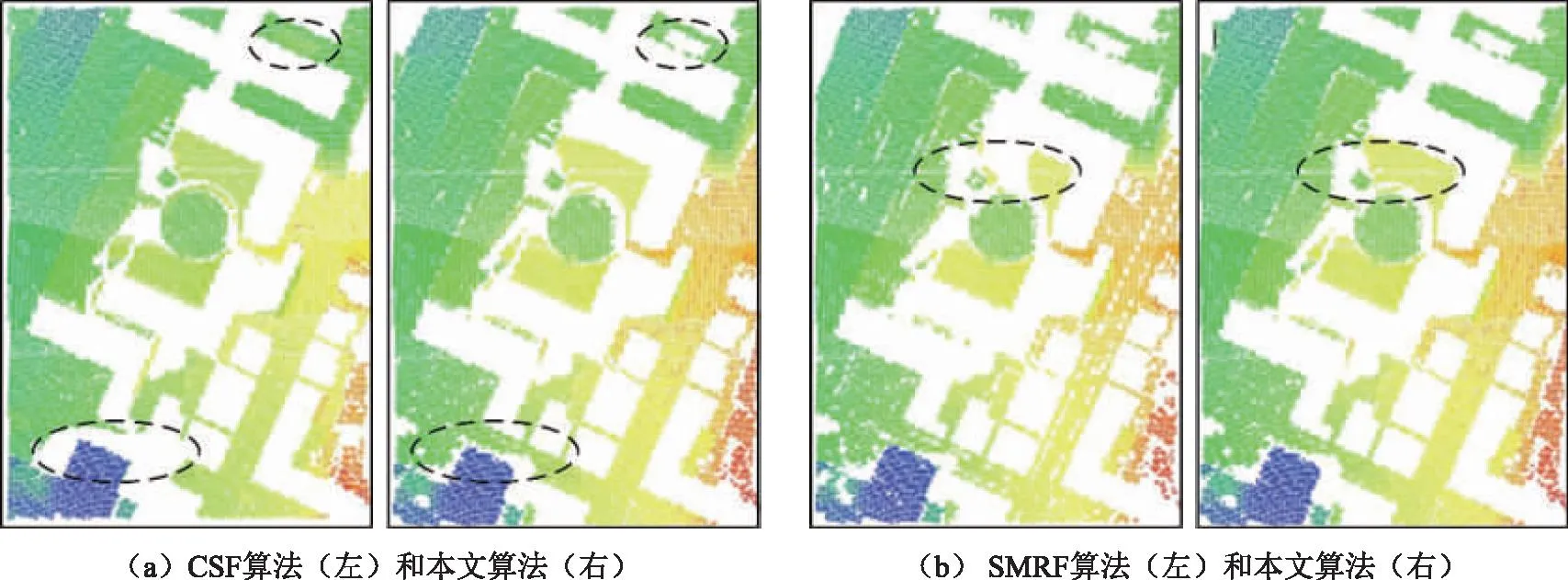
图8 不同算法对Samp23的滤波效果对比

Samp52数据是流经河流的山坡地带。如图9所示,圆圈标注区域都在坡峰附近,其侧面过于陡峭,地形变化剧烈,CSF算法和SMRF算法在应对该区域时都容易把地面点错误判断成非地面点;同时河岸附近存在大量低矮植被和建筑物,也对滤波过程造成了干扰。对比结果显示,虽然本文算法在该区域具有相对更好的滤波效果,但也受到陡峭地形和低矮地物的干扰,出现较大的Ⅱ类误差。

图9 不同算法对Samp52的滤波效果对比

为了更客观、清楚地评判改进算法的优劣性,对本文算法的滤波结果与已测试过的其他4种滤波算法的精度进行比较分析,包括CSF滤波算法、移动曲面滤波算法、PTD滤波算法和SMRF滤波算法。如图10所示,在5种滤波算法对8个不同地形的实验中,CSF算法在Samp12、Samp23、Samp31、Samp51实验区总误差小于11.5%,Samp53区域总误差为6.6%;移动曲面算法在Samp12、Samp31、Samp42研究区总误差小于10.1%;PTD算法在Samp31、Samp42区域总误差小于9%,在实验区Samp51、Samp52、Samp53总误差小于5.2%;SMRF算法在区域Samp12、Samp23、Samp31、Samp52的总误差小于11.2%;本文算法在实验区总误差均小于5.4%,在实验区Samp12、实验区Samp42的总误差接近于0。比较发现,本文方法的平均总误差最小,同时各个实验区的Ⅰ类误差始终小于8.1%,证明该算法具有很好的适用性,能够有效地降低点云误差。

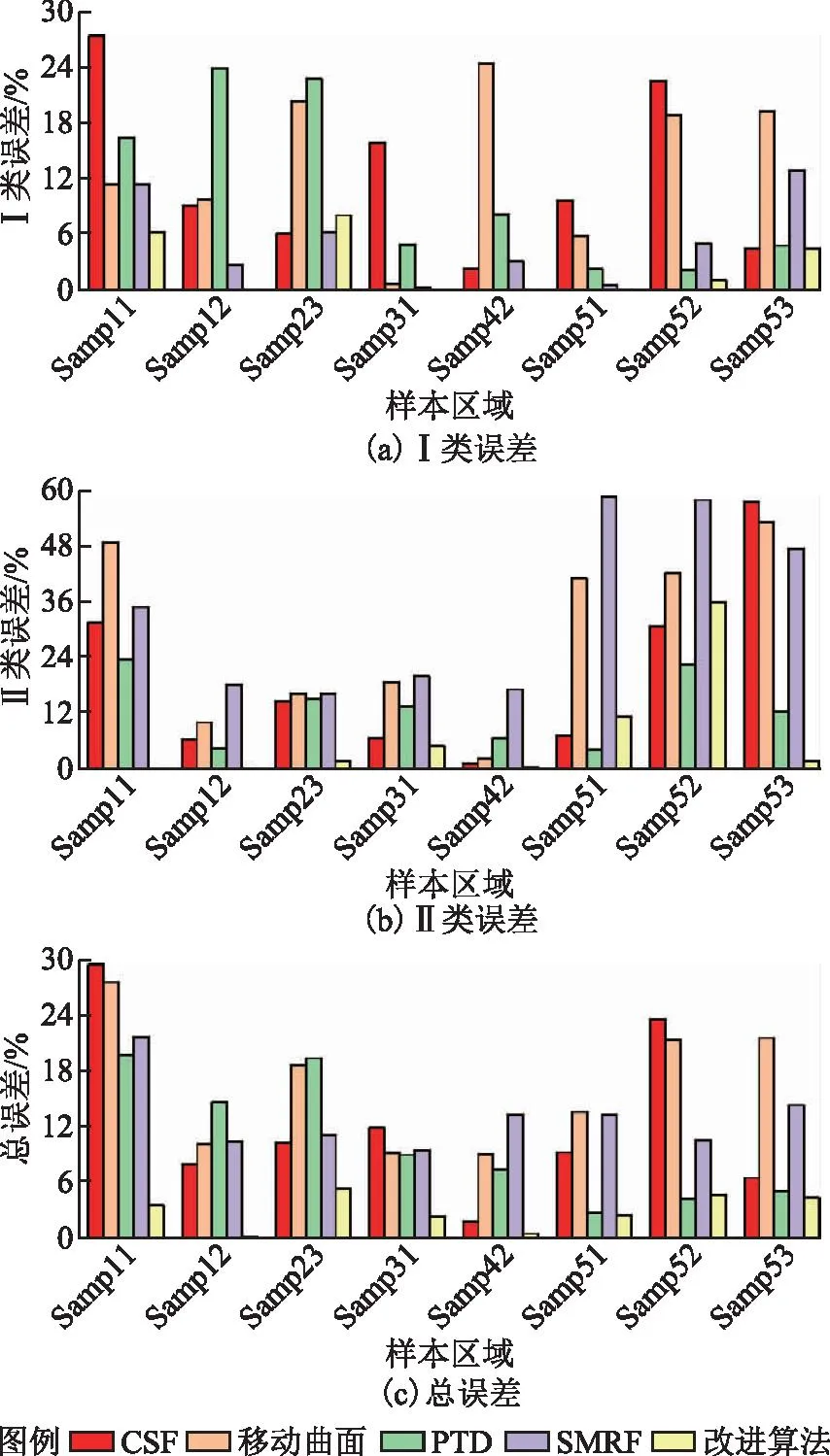
图10 5种算法的滤波精度比较

3 结束语

本文结合简单形态学滤波,改进了地面平面拟合算法;利用地面平面拟合算法对归一化点云的滤波优势,显著提高了算法精度;通过渐进移动窗口构建多个平面模型,减少迭代步骤,克服单一阈值的局限性;针对多个平面的合并问题,采用空间向量的后处理方法,以点云密度控制二面角阈值,避免过度分割。

算法滤波精度得到有效提高。与SMRF算法比较,本文算法的中误差降低了3.3 cm,平均绝对误差降低了2.0 cm。与CSF算法、移动曲面算法、PTD算法和SMRF算法比较,本文算法的平均总误差分别减少8.8%、12.5%、6.5%和9.2%,能够在抑制Ⅰ类误差增大的同时大幅降低Ⅱ类误差,证明该算法能够有效地降低点云误差。

滤波方法适用于多数地形条件。实验区包含建筑物、公路、植被、陡坡等不同地物特征,基本对应常见地形,本文算法在实验区总误差均小于5.4%,在实验区Samp12、实验区Samp42的总误差接近于0,同时各个实验区Ⅰ类误差始终小于8.1%,表明本文算法能够适用于多数地形条件。